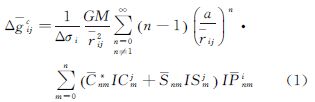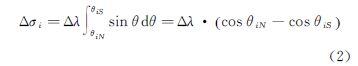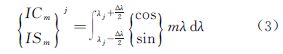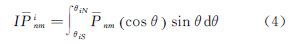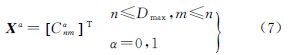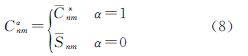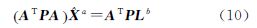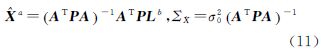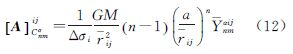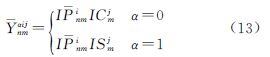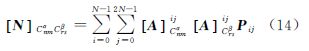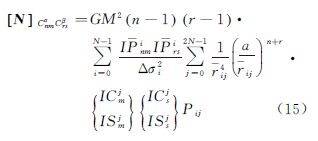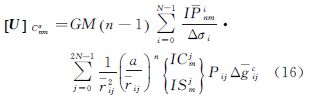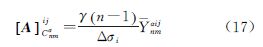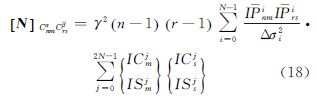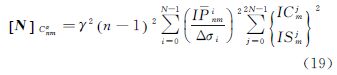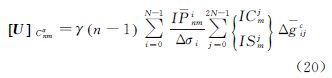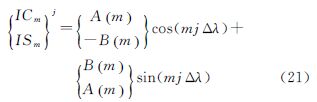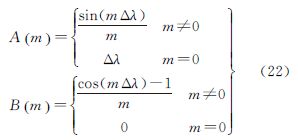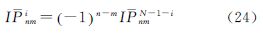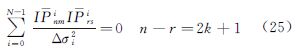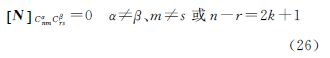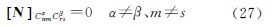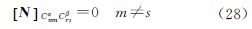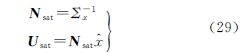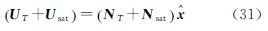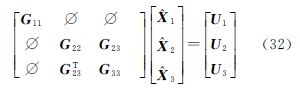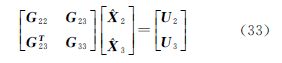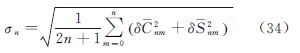2. 西安测绘研究所，陕西 西安 710054；
3. 61206部队，北京 100042
2. Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China;
3. 61206 Troops,Beijing 100042,China
1 引 言
自1937年首次推出6阶地球重力位模型开始，经过70多年的发展，地球重力场模型已经发展到2160完全阶次。在模型的构建方法中，基于数值积分方法在对精度评估方面的缺陷，最小二乘方法已成为目前国际上构建重力场模型的主要方法。2008年NGA(US National Geospatial-Intelligence Agency)发布的目前精度最好的超高阶地球重力场模型EGM2008的解算采用最小二乘方法，在具有高质量重力数据的地区，EGM2008模型大地水准面与独立的GPS/水准数据之间差异小于±10 cm，其确定的垂线偏差相对于独立的天文大地垂线偏差的差异在±1.1″和±1.3″。我国由于全球数据的缺乏，目前所构建的超高阶地球重力场模型精度较差，且由于均采用数值积分方法，没有给出合适的精度评价。另外，随着卫星重力的不断发展，获得的卫星重力场模型不断精化超高阶地球重力场模型中低阶部分，最小二乘方法在联合地面重力数据和卫星重力场方面也起到了至关重要的作用。所以，要构建我国自己的高精度的超高阶全球重力场模型，一方面要获取全球高质量的重力数据，另一方面应当发展当前普遍使用的最小二乘方法[1, 2, 3, 4, 5, 6]。
重力场模型构建过程中，由于观测方程中的未知量(模型位系数)太多，且观测值数量巨大，所以在构建法方程以及法方程求解过程中会遇到海量计算问题，直接求解是不可行的，而球谐函数的正交特性使得由观测方程得到的法方程矩阵是一稀疏矩阵，那么，通过对未知数的重新排列，获得具有块对角形式的法矩阵，这对于法方程的解算具有重要作用[7, 8]。本文重点讨论了利用块对角最小二乘方法构建全球重力场模型以及联合卫星重力场模型的方法，并通过试验计算，与数值积分方法进行了相关比较。
2 基本原理全球格网平均重力异常采用球谐分析求解地球重力场模型的基本观测方程为[9, 10, 11, 12, 13, 14, 15, 16, 17]
式中
rij为第i行第j列格网平均重力异常的地心向径；λj表示第j列格网中点经度；(θiN、θis)表示第i行格网的北边界纬度与南边界纬度；a为正常椭球的长半径；Δgijc为经过椭球改正、大气改正、二阶梯度项改正等归算后满足调和边值问题的地面格网平均重力异常值；Cnm*和Snm即为所求的一组重力场模型位系数。
将观测方程式(1)表示为最小二乘方法中的通用表达式
式中
其中，D表示所恢复模型的阶数。
F函数是关于X的线性方程，根据线性方程组最小二乘平差模型，有
设P为重力异常权矩阵，则可以得到法方程
最终可得位模型系数的解及相应的协方差阵
根据上述公式能够求得最终的位系数，然而对于利用全球5′×5′格网重力异常估计2159阶位系数(不包括C00)，A矩阵大小为9 331 200×4 665 596，法矩阵ATPA大小为4 665 596×4 665 596，所以庞大的计算量目前是不可能完成的。顾及庞大的计算量，为了提高计算效率，有必要讨论法方程在地面重力异常数据满足以下条件时的一些特殊性质：
(1) 数据分布于一旋转曲面上(例如旋转椭球面上)。
(2) 格网数据覆盖整个曲面，且经度方向的分辨率一致。
(3) 数据中误差与经度无关，即数据的权重不依赖于经度的大小。
(4) 数据权重关于赤道对称，即纬度φ与－φ的格网数据精度相同。
显然，满足以上条件的权矩阵是个对角阵。根据式(1)，矩阵A的各个元素由式(12)、式(13)表示
根据法矩阵N=ATPA以及满足以上条件的P为对角阵，有
即
这里要注意区分变量r和rij，相应的U=ATPLb的元素为
理想情况下，假设N×2N个重力异常分布于半径为a的球面上，且重力异常都有相同的标准差σ，那么权阵P=σ2I，在不影响问题讨论下令σ=1以简化推导，γ=GM/a2，则式(16)可简化为
由式(3)，能进行如下变换
式中
根据正、余弦函数的正交性，能够证明
另外，全球格网数据分布是关于赤道对称的，满足θi=π－θN－1－i，再根据缔合Legendre函数的特性，有
因此
综合式(23)与式(25)考虑，式(18)中的法矩阵满足
法矩阵在计算数据满足以上4个条件的情况下，呈稀疏矩阵，有助于提高计算效率。满足式(26)条件下，通过对法方程中的未知系数进行重新排序，生成具有较好的结构的块对角矩阵，这种块对角法矩阵称为第1类块对角近似BD-1(block-diagonal-1)。文献[11]中给出了6种排列方式，表 1简要描述了这6种排列方式。
| 位系数 排列方式 | N=3 |
| Ⅰ | C20，C21，C22，C30，C31，C32，C33，S21，S22，S31，S32，S33 |
| Ⅱ | C20，C21，C22，S21，S22，C30，C31，C32，C33，S31，S32，S33 |
| Ⅲ | C20，C21，S21，C22，S22，C30，C31，S31，C32，S32，C33，S33 |
| Ⅳ | C20，C30，C21，C31，C22，C32，C33，S21，S31，S22，S32，S33 |
| Ⅴ | C20，C30，C21，C31，S21，S31，C22，C32，S22，S32，C33，S33 |
| Ⅵ | C20，C30，C21，S21，C31，S31，C22，S22，C32，S32，C33，S33 |
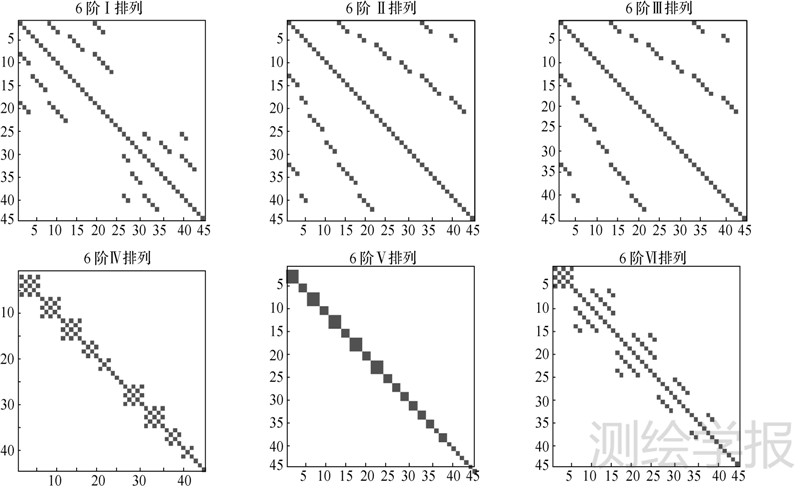
上述排列方法中，对Ⅴ排列方式进行进一步细化，区分n-m为奇数偶数的情况，例如，对于N=6的排列，排列顺序记为C20、C40、C60、C30、C50、C21、C41、C61、C31、C51、S21、S41、S61、S31、S51、C22、C42、…。下面采用了全球8×16的格网平均重力异常计算N=6情况下法矩阵[N]的情况，其中权矩阵P采用单位阵I，具体见图 1，图中白色区域表示为0元素，黑色像素点为非零元素。
|
| 图 1 6种系数排列方式下的法矩阵稀疏状态 Fig. 1 Sparse status of normal matrix in 6 kinds of sorting patterns |
在实际计算过程中，数据经过空白区的填补和数据解析延拓等处理后能近似满足(1)、(2)条件，但是因为各个局部区域的测量精度都存在差异，所以一般情况下不满足(3)、(4)条件。所以当上述4个条件只有(4)条件不满足时，法矩阵
该块对角形式称为第2类近似块对角(BD-2)结构，第3类近似块对角结构(BD-3)结构的法矩阵
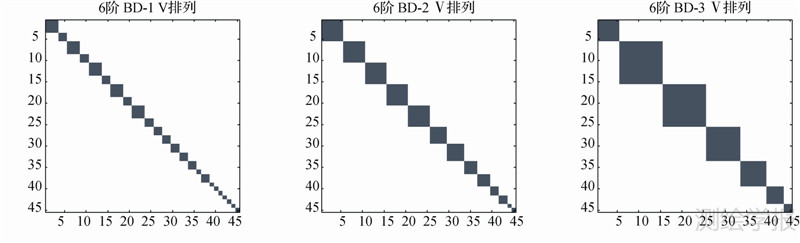
下面根据上述定义式计算Ⅴ排列下，3种近似块对角结构的法矩阵形式：
通过图 2能够很清晰地看出，对于Ⅴ排列，重力异常数据满足上述条件越多，其法矩阵中非零元素越少，“块”越小，块对角形式越简单。说明在模型计算过程中，随着全球重力异常数据全球覆盖不断完善，分辨率和精度不断提高，法矩阵可近似为越来越简单的形式，便于模型的快速求解。
|
| 图 2 3种近似条件下BD-1、SD-2、BD-3的法矩阵特点 Fig. 2 Normal matrix characters of BD-1,BD-2 and BD-3 in 3 kinds of approximate conditions |
当模型位系数最大阶数为Nmax、采用Ⅴ排列情况下，3种BD结构的特点统计如表 2所示。
| BD-1 | BD-2 | BD-3 | |
| 最大“块”的大小 | int(Nmax/2)× int(Nmax/2) | Nmax－1 | 2Nmax－2 |
| “块”的总个数 | 4Nmax | 2Nmax+1 | Nmax+1 |
| 非零元素的比例 | 0.09 | 0.19 | 0.37 |
根据上述理论，相比数值积分方法，块对角最小二乘具有以下特点：①数值积分方法确定的每个系数彼此之间是相互独立的，而对于块对角最小二乘而言，即使使用的重力异常数据之间不相关，但确定的系数之间也是相关的；②数值积分方法不能对重力异常数据进行精度评估，块对角最小二乘方法可以；③使用30′×30′离散数据，根据Nyquist法则，数值积分方法能够恢复到360阶，而块对角最小二乘只能最大恢复到359阶。
3 块对角联合卫星重力场模型
大多数模型求解中均使用最小二乘方法联合卫星重力场模型得到最终的联合解。随着卫星重力场模型以及地面重力观测数据的不断完善，块对角方法在联合卫星重力场模型方面也在发生着变化。
根据卫星重力场模型及其误差协方差矩阵，能够完全再现计算该模型的法方程和对应的U，误差协方差矩阵的逆对应于法矩阵
同样根据地面数据，能够得到地面的法方程
如果使用简单的等权相加来联合上面两个法方程，即将卫星的法矩阵叠加到地面法矩阵上，就能够得到联合后的法方程
上式求得的未知数就是概念上的联合解，在实际解算过程中，必须考虑两种法方程联合中的权重分配问题，该问题本文暂不讨论。
3.1 早期卫星重力场模型的联合在CHAMP(challenging mini-satellite payload)、GRACE(gravity recovery and climate experiment)等重力卫星发射之前，早期的卫星重力场模型是综合卫星轨道跟踪、卫星激光测距等手段求得的。文献[10]中计算分析了使用地面数据计算的法矩阵和卫星重力场模型的协方差矩阵(即法矩阵)中非块对角元素的大小及其影响，结果显示，在不损失结果精度的情况下，很难将当时的卫星重力场模型的法矩阵近似为上述任何3种块对角(BD)型，因此在前期模型构建过程中使用的卫星重力场模型协方差阵，没有稀疏特性，但因为其阶数较低，计算能够实现。另外，由于地面数据的精度和分布较差，所以地面观测数据的法矩阵采用块对角近似条件最弱的BD-3。
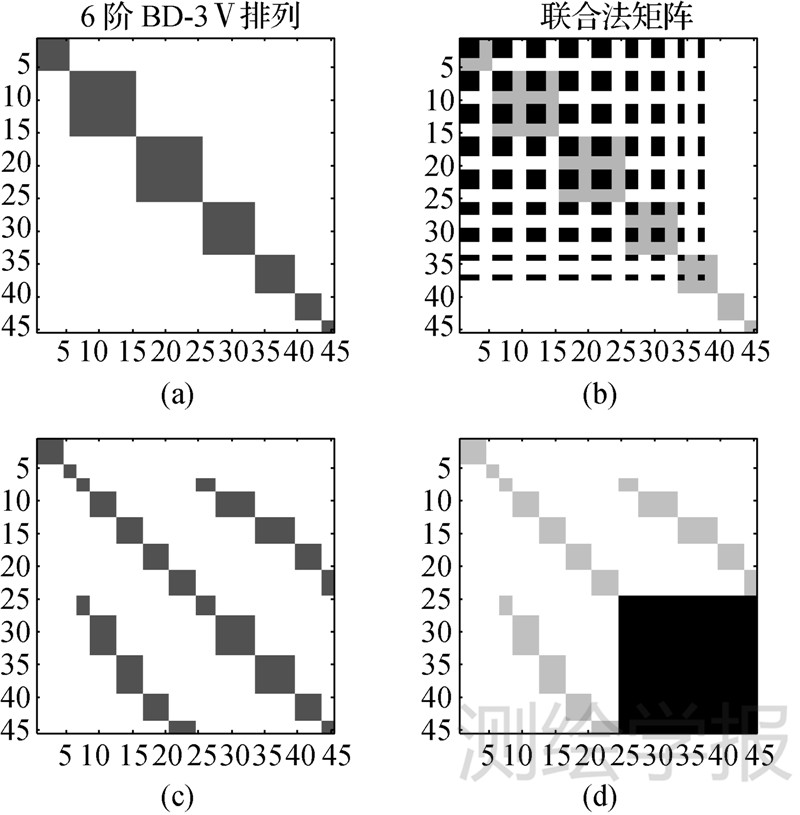
联合卫星重力场模型的计算过程中，使用了文献[10]中所谓的“falling kite”结构，见图 3(d)。本文利用全球8×16格网数据模拟计算地面阶数Dmax=6的法矩阵，并联合阶数Dsat=4的卫星法矩阵。图 3(a)是地面法矩阵BD-3结构，与之对应的卫星系数也按Ⅴ排列，则其占满的法矩阵的重新分布情况见图 3(b)黑色部分，显然这种联合后的法矩阵会产生一个很大的“块”，几乎是整个法矩阵的大小，所以该排列形式不利于高效的计算。
|
| 图 3 最小二乘中法矩阵的联合 Fig. 3 Combination of normal matrix in LS combination solution |
为构造最小的“块”，将要求解的未知数Cnm、Snm分为3组：①n＞Dsat,m＞Dsat；②n＞Dsat,m≤Dsat；③n≤Dsat,m≤Dsat。每一组中的未知数都按之前的Ⅴ方式排列，得到的地面法矩阵的结构见图 3(c)，卫星法矩阵与地面联合的法矩阵见图 3(d)。
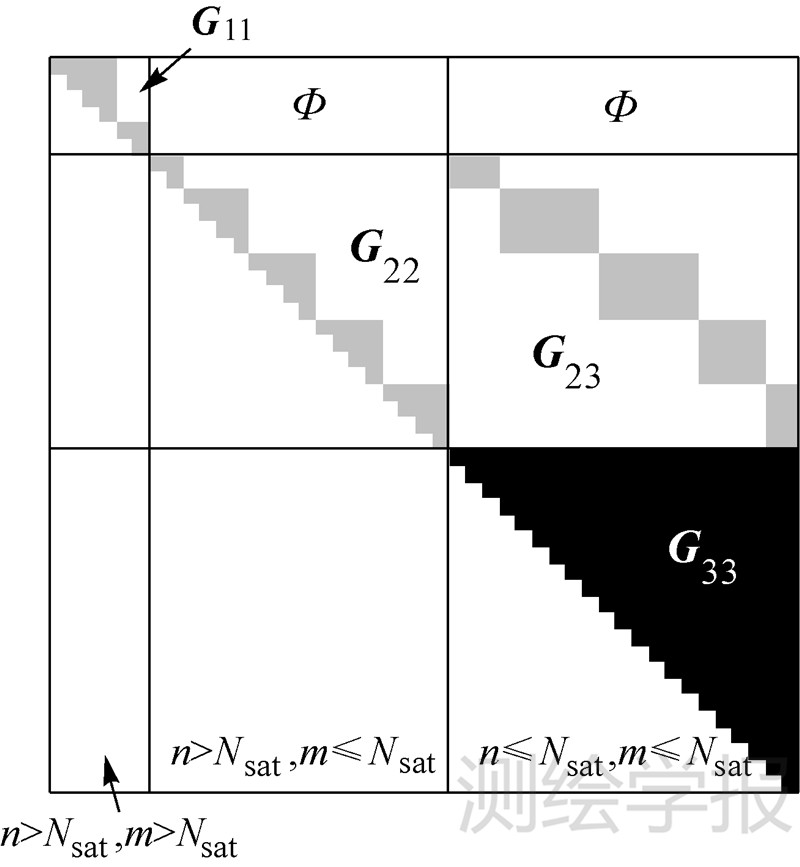
对于“falling kite”结构的计算，采用分组方法，考虑到法矩阵为对称矩阵，将其按照图 4分割为若干个小矩阵，其中G11和G22是“纯地面”的块对角阵，G23由非零元素的矩形块构成，与G22有相同的行分割，G33则是包含地面和卫星信息的对称矩阵。
|
| 图 4 联合法方程矩阵求解示意图 Fig. 4 Sketch map of combination with normal matrix |
根据式(32)，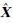
1可单独利用块对角G11求解而不影响其他系数，剩下的部分为
上式系数矩阵G为对称矩阵，可对其进行Cholesky分解来快速稳定的计算。由于最终模型的协方差阵的计算非常复杂，故在实际解算过程中，只计算以下3个内容：①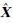1系数的块对角协方差矩阵G11－1；②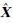2每个系数的方差；③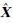3系数的满协方差矩阵[9]。
早期模型在联合过程中使用了“falling kite”结构的主要原因是因为在没有损失结果质量情况下很难将卫星模型系数的法方程近似为任何块对角型。而在最新超高阶重力场模型的联合中，因为使用的全球数据分辨率及精度高，全球分布较完善，所以在其求解过程中使用的是条件最严格的BD-1块对角近似，另外，随着重力卫星技术的不断发展，高精度的GRACE-only模型也可以获取。GRACE信息的误差特性允许其协方差矩阵采用块对角近似，因此，在联合过程中将GRACE-only模型的协方差矩阵近似为BD-1，与地面法方程叠加，而舍弃之前的BD-3结构和“falling kite”结构，在不损害结果质量下使得联合解算既简洁又高效。此外，由于椭球谐分析比球谐分析精度好，所以模型构建均采用椭球谐分析，而在球谐系数和椭球谐系数转换过程中，并没有改变法矩阵的块对角形式，这一点对于能够采用块对角方法来计算模型是至关重要的[18, 19, 20]。
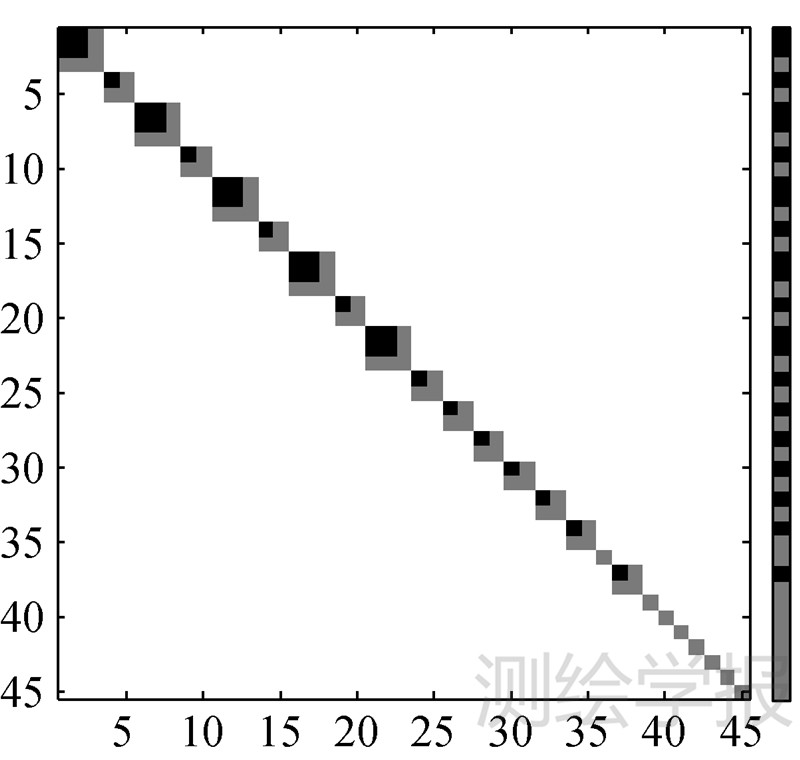
将卫星重力场模型Dsat=4的BD-1法矩阵结构叠加到地面数据确定的Dmax=6的BD-1法矩阵上，对应U矩阵的叠加与N矩阵对应，见图 5。
|
| 图 5 GRACE-only法方程联合情况 Fig. 5 Sketch map of GRACE-only normal equation combination |
根据图 5，显然可以一次性联合解一个对角块，这样，对于2160阶次的超高阶地球重力场模型，所需要求逆的最大的对称矩阵是1080×1080规模的，这对于目前的计算水平来说并不算什么，这种近似相比于早期模型联合卫星模型，大大简化了平差难度。
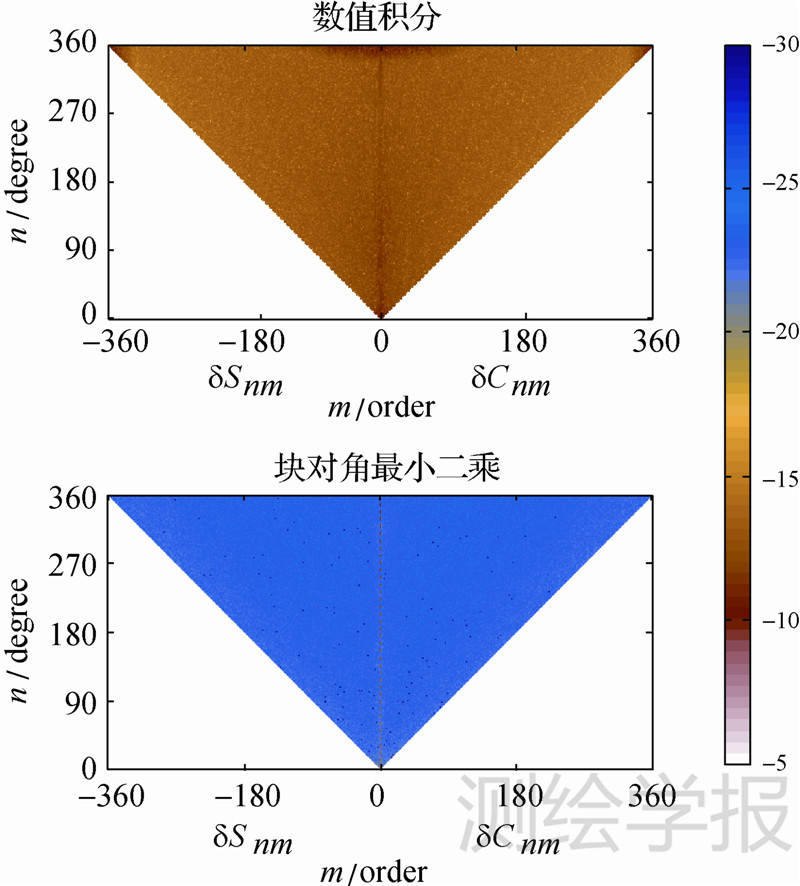
4 试验计算分析为验证块对角最小二乘在构建全球重力场模型的优势及其实用性，本文使用3.2 GHz主频、2 GB内存计算机，基于vs2008试验平台，进行模拟计算。使用块对角方法计算模型过程中，矩阵A最大，计算ATPA最耗时间，当计算一个2160阶的超高阶地球重力场模型，计算法矩阵中最大的“块”所使用的A的大小为(2160－1)(2160+3)×1080，开辟该数组需要至少37.6 GB内存，所以基于硬件限制，本文模拟计算360阶模型。首先使用EGM2008模型截至360阶的模型系数模拟生成全球30′×30′格网平均重力异常，因为对于30′×30′分辨率数据，最小二乘方法只能恢复到359阶，所以使用模拟生成的格网平均重力异常采用数值积分以及块对角最小二乘两种方法恢复EGM2008模型前359阶位系数，结果比对见图 6。
|
| 图 6 模型恢复误差的比较 Fig. 6 Comparison of error of recovered model |
图 6中通过统计恢复系数与EGM2008系数差的绝对值的自然对数，获得数值积分方法和块对角最小二乘方法恢复模型位系数的精度情况。图 6中明显看出块对角最小二乘方法恢复的模型整体精度比数值积分方法高出10个数量级，唯独在偶阶带谐项C2k,0有较大误差。
由基本原理可知，数值积分方法求解的位系数之间是相互独立的，而块对角最小二乘方法求得的位系数是相关的，因此在使用块对角最小二乘方法求解模型位系数过程中，必须根据Nyquist法则对重力异常数据的频谱能量进行限制，即无论使用多大分辨率数据恢复n阶位系数，每一离散数据中必须只包含0～n阶系数的贡献。下面以30′×30′格网平均重力异常恢复240阶位系数为例，进行分析计算。
首先使用EGM2008模型截至360阶的模型系数模拟生成全球30′×30′格网平均重力异常Δg0～360，采用数值积分方法恢复0～360阶模型位系数，利用恢复系数中的241～360阶计算包含241～360阶频谱能量的30′×30′格网平均重力异常Δg241～360，采用Δg0～240=Δg0～360－Δg241～360计算包含0～240阶频谱能量的30′×30′格网平均重力异常，利用该30′×30′格网重力异常Δg0～240，采用块对角最小二乘方法恢复0～240阶模型系数。使用EGM2008作为标准模型，计算两种方法恢复的360阶和240阶模型系数的误差阶RMS并进行比较，比较结果见图 7，其计算公式为
|
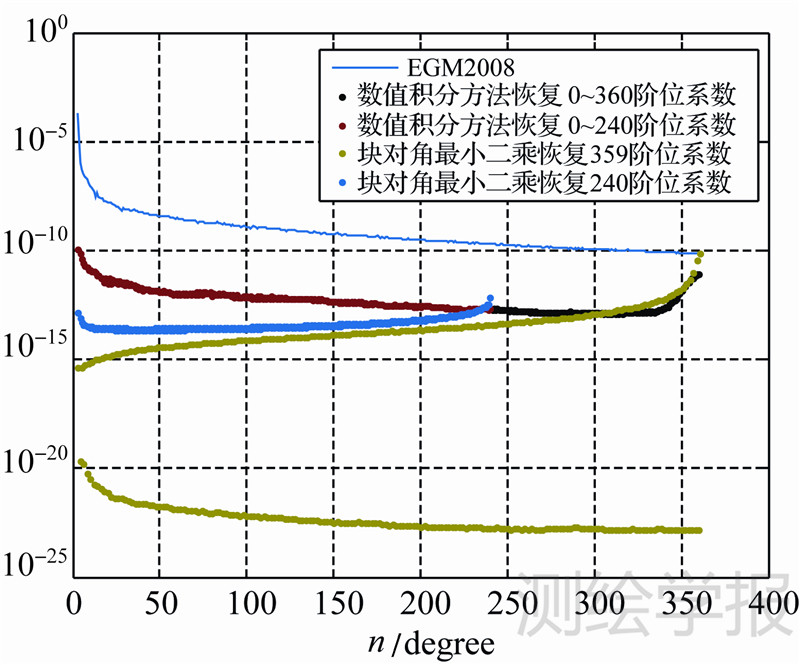
| 图 7 误差阶RMS比较 Fig. 7 Comparison of error degree RMS |
由图 7可看出，无论恢复359阶还是240阶模型位系数，块对角最小二乘方法恢复模型系数的误差阶RMS明显小于使用数值积分方法恢复的模型系数。其中块对角恢复的359阶位系数的误差阶RMS曲线分为两条，上面的是偶数阶，下面是奇数阶，其之间的差异由偶阶带谐项C2k,0的计算误差引起的，而恢复的240阶系数由于奇阶和偶阶系数之间的相关性发生频谱叠效应，所以误差阶RMS曲线为一条。通过图 7比较分析可知，块对角最小二乘相比数值积分方法，能够更好地恢复模型，再加上其联合卫星重力场模型简洁高效的特点，越来越凸显其在模型构建中的优势。
5 结 论相比于数值积分方法，基于块对角最小二乘构建的全球重力场模型的优势主要体现在：①联合中低阶卫星重力场模型更加简洁高效；②能够给出所构建的全球重力场模型每阶位系数的精度评价，相比中低阶部分采用最小二乘平差方法、高阶部分采用数值积分方法构建的模型，块对角最小二乘方法避免了误差谱曲线在计算方法变化的阶数部分不连续的现象；③模型恢复的精度更高。基于以上优势，加上目前的计算能力已经能够满足使用块对角最小二乘方法求解2160阶超高阶地球重力场模型，因此，有必要进一步加强块对角最小二乘方法计算模型方面的研究，这对于我国构建自主高精度超高阶地球重力场模型，提高我国区域大地水准面的精度具有重要作用。
| [1] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 [J]. Journal of Geophysical Research, 2012, 117(04406）. |
| [2] | WANG Zhengtao, DANG Yamin, CHAO Dingbo, et al. Theory and Methodology of Ultra-high-degree Geopotential Model Determination[M] Beijing: Surveying and Mapping Press, 2011.(王正涛,党亚民,晁定波. 超高阶地球重力场模型确定的理论与方法[M]. 北京: 测绘出版社, 2011.) |
| [3] | ZHENG Wei, XU Houze, ZHONG Min, et al. Progress and Present Status of Research on Earth’s Gravitational Field Models[J]. Journal of Geodesy and Geodynamics, 2009, 30(4): 83-90.(郑伟,许厚泽,钟敏,等. 地球重力场模型研究进展和现状[J]. 大地测量与地球动力学. 2009, 30(4): 83-90.） |
| [4] | NING Jinsheng. The Progress in the Earth’s Gravity Field in China[J]. Northeast Surveying and Mapping, 2002, 25(4): 6-9.(宁津生. 我国地球重力场研究的进展[J]. 东北测绘, 2002, 25(4): 6-9.） |
| [5] | SHU Chanfang, LI Fei, HAO Weifeng. Evaluation of EGM 2008 and Its Application Analysis over a Particular Region of China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 919-922.(束蝉方,李斐,郝卫峰. EGM2008模型在中国某地区的检核及适用性分析[J]. 武汉大学学报:信息科学版, 2011, 36(8): 919-922.） |
| [6] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289.(章传银,郭春喜,陈俊勇,等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报. 2009, 38(4): 283-289.） |
| [7] | NING Jinsheng, QIU Weigen, TAO Benzao.Theory of Geopotential Model Determination[M]. Wuhan:Wuhan University Press, 1990.(宁津生,邱卫根,陶本藻. 地球重力场模型理论[M]. 武汉: 武汉大学出版社, 1990.) |
| [8] | LIU Xiaogang. Theory and Methods of the Eath’s Gravity Field Model Recovery from GOCE Data[D]. Zhengzhou: Information Engineering University, 2010.(刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2010.） |
| [9] | PAVLIS N K, The Block-diagonal Least-squares Approach[R]. Washington D C: NASA Goddard Space Flight Center, 1998. |
| [10] | LEMOINE F G. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96[R]. Washington D C: NASA Goddard Space Flight Center, 1998. |
| [11] | PAVLIS N K. Modeling and Estimation of a Low Degree Geopotential Model from Terrestrial Gravity Data[R]. Columbus: Ohio State University, 1988. |
| [12] | RAPP R H, PAVLIS N K. The Development and Analysis of Geopotential Coefficient Models to Spherical Harmonic Degree 360[J]. Journal of Geophysical Research, 1990, 95(B13): 21885-21911. |
| [13] | COLOMBO O L. Numberical Methods for Harmonic Analysis on the Sphere[R]. Columbus: Ohio State University, 1981. |
| [14] | LU Zhonglian. Theory and Method of Earth’s Gravity[M]. Beijing: The People’s Liberation Army Press, 1996.(陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.) |
| [15] | HEISKANEN W, MORITZ H. Physical Geodesy[M]. Beijing: Surveying and Mapping Press, 1979.(海斯卡涅W A, 莫里斯H. 物理大地测量学[M]. 北京: 测绘出版社, 1979.) |
| [16] | HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. 2nd edition. Berlin: Springer, 2005. |
| [17] | LI Jiancheng,CHEN Junyong, NING Jinsheng, et al. Approximation Theory of the Earth Gravity Field and Determination of the Chinese Gravity Geoid Model 2000[M]. Wuhan: Wuhan University Press, 2006.(李建成,陈俊勇,宁津生,等. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2006.) |
| [18] | PVLIS N K, SALEH J. Error Propagation with Geographic Specificity for Very High Degree Geopotential Models in Gravity[C]//IAG Symposia of Geoid and Space Missions. Berlin: Springer,2004. |
| [19] | JEKELI C. The Exact Transformation between Ellipsoidal and Spherical Harmonic Expansions[J]. Manuscripta Geodaetica, 1987, 13: 106-113. |
| [20] | GLEASON D M. Comparing Ellipsoidal Corrections to the Transformation between the Geopotential’s Spherical and Ellipsoidal Spectrums[J]. Manuscripta Geodaetica, 1988, 13: 114-129. |