混合像元分解过程是要从混合像元中识别不同类型的地物(端元),并求出其在混合像元中所占的比例(丰度),是高光谱遥感影像分析的核心问题之一。混合像元线性分解的方法有很多,大体上分为基于几何的、基于统计的和新近发展起来的基于稀疏回归的三大类方法[1]。基于几何和统计的方法,解混精度依赖于端元提取的准确性,在影像场景复杂、像元普遍混合程度高时,纯净像元存在性的假设难以满足,很难准确地提取端元光谱。基于稀疏回归的混合像元分解方法是一种半监督的解混方法[2, 3, 4],它利用已有的端元光谱库[5]作为先验信息,将像元表示成端元光谱库中某些端元的线性组合。该方法不需要在影像中提取端元,也不要求影像中每个端元必须有纯净像元对应,在像元普遍混合程度较高时仍能取得较好的效果。一个像元含有的端元数目通常小于整幅影像所含有的端元数目,更远远小于端元光谱库中端元的数目,即像元用端元线性表示时丰度值具有稀疏性[6, 7]。基于稀疏回归的解混算法在解混过程中加入了丰度的稀疏性约束,得到的结果更符合实际情况。然而光谱库中端元光谱的相似度一般较高,影响了基于稀疏回归解混方法的精度。
大部分混合像元分解的算法都基于影像的光谱分析,却忽略了影像的空间信息。然而影像在空间上有一定的连续性,像元与其邻近像元的端元以及对应丰度有很强的相关性。近年来很多学者研究如何利用高光谱影像丰富的空间信息来提高混合像元分解的精度,提出了很多改进算法。文献[8, 9, 10, 11, 12, 13, 14]通过影像空间分析更准确地提取端元光谱。文献[13]通过聚类或者分割算法自适应地提取光谱纯净区域,避免了窗口大小的选择对算法的影响,然后在空间同质区提取端元。 文献[14]进一步提出空间同质指数,并将空间同质指数和光谱纯净指数融合在一起辅助提取端元。另外一些则是在原来基于光谱空间分析算法的目标优化函数里加入空间平滑性约束[15, 16, 17, 18]。其中文献[18]在稀疏解混模型中加入空间全变分正则项,在稀疏解混算法(sparse unmixing via variable splitting and augmented lagrangian,SUnSAL)的基础上提出了SUnSAL-TV(SUnSAL and total variation)算法,使得解混结果既保持稀疏性又保持一定的空间平滑性。这些方法对不同的空间邻域建立了一致的空间平滑性模型;然而端元丰度的空间分布异常复杂,平滑性并不能保持一致。
2 基于稀疏回归的解混模型和全变分空间正则化稀疏解混
混合像元的线性表示模型可以表示为y=Mα+n[19],其中y是一个L维的列向量,表示像元反射光谱(L是影像的光谱波段数);M是一个L×q维矩阵,这个像元中含有q个端元,每一列表示一个端元的光谱;α是一个q维向量,表示每个端元对应的丰度;n是L维的加性噪音。
基于稀疏回归的解混模型将端元光谱库作为先验信息,端元光谱库是人工提取的地物光谱信息。这时影像解混就不需要进行端元提取,也不需要假设影像中每个端元都存在纯净像元。假设端元光谱库中有m个端元,令A∈RL×m,A的每一列是一个端元光谱向量,则混合像元可以用光谱库中端元线性表示
将混合像元分解问题通过稀疏回归模型来表示,式(2)是其中一种等价的稀疏回归模型[2]
式中,
 项表示回归的Ax对观测值y的拟合程度;
项表示回归的Ax对观测值y的拟合程度; 是稀疏性条件约束;λ是调整目标函数中两项的权值。由于光谱的可变性,通常丰度的“和为一”条件并不能被满足,模型中只加入了丰度的非负性条件约束。式(2)可以通过SUnSAL[2]、ISMA(iterative spectral mixture analysis)[20]、OMP(orthogonal matching pursuit)[21]等算法及其变形算法求解。文献[2]比较了这些稀疏解混算法,认为从整体上来说SUnSAL算法及其变形算法的解混效果最好,因此本文以SUnSAL算法为例,讨论在稀疏解混算法中加入空间信息。
是稀疏性条件约束;λ是调整目标函数中两项的权值。由于光谱的可变性,通常丰度的“和为一”条件并不能被满足,模型中只加入了丰度的非负性条件约束。式(2)可以通过SUnSAL[2]、ISMA(iterative spectral mixture analysis)[20]、OMP(orthogonal matching pursuit)[21]等算法及其变形算法求解。文献[2]比较了这些稀疏解混算法,认为从整体上来说SUnSAL算法及其变形算法的解混效果最好,因此本文以SUnSAL算法为例,讨论在稀疏解混算法中加入空间信息。
文献[18]考虑丰度值的空间平滑性,在式(2)中加入空间全变分(TV)空间正则项约束,如式(3)所示
式中,Y∈RL×N是整幅高光谱影像数据,N是影像中像元的个数;X∈Rm×N是影像的端元丰度;
 是Frobenius范数;
是Frobenius范数; 是第i个像元的丰度向量;TV(X)是TV正则项,
是第i个像元的丰度向量;TV(X)是TV正则项, 表示像元和其邻接像元的丰度差,ε表示影像中水平和垂直相邻的像元组;λTV表示在目标函数中空间项对应的权重。令Hhxi,j=xi,j-xi,j+1,Hvxi,j=xi,j-xi+1,j,
表示像元和其邻接像元的丰度差,ε表示影像中水平和垂直相邻的像元组;λTV表示在目标函数中空间项对应的权重。令Hhxi,j=xi,j-xi,j+1,Hvxi,j=xi,j-xi+1,j, ,则TV(X)≡
,则TV(X)≡ ,式(3)可以表示为
,式(3)可以表示为式中,
 是指标函数,当向量xi的所有元素都大于或等于0时,函数值为0,否则为+∞。式(4)可以基于ADMM(alternating direction method of multipliers)策略求解[18]。
3 基于空间同质分析的稀疏解混
是指标函数,当向量xi的所有元素都大于或等于0时,函数值为0,否则为+∞。式(4)可以基于ADMM(alternating direction method of multipliers)策略求解[18]。
3 基于空间同质分析的稀疏解混
TV正则项表示了丰度分布的空间平滑性,然而这种平滑性在影像空间中并不一致。有些像元与其邻近像元的光谱很相似,叫做同质像元[12],相邻同质像元的地物组成成分也很可能一样,对应的丰度也应该相近,即在同质像元组成的区域,丰度分布保持着很强的空间平滑性。另外一些像元与邻近像元相比,光谱变化较大,表明它们的地物组成和丰度都有较大的变化,这些区域丰度分布的空间平滑性较低。影像的空间同质分析通过比较像元与其邻域内像元之间的光谱相似性得到像元的空间同质性,能较好地度量影像的空间平滑性。定义像元的同质指数hi∈[0,1]与它的邻域窗口内其他像元光谱相似性的加权平均值,由下式计算
式中,Pi,j和Pr,c是分别位于影像中(i,j)和(r,c)处的像元;ω是空间权重参数;S(Pr,c,Pi,j)表示像元Pi,j和Pr,c的光谱相似性;Ωd(Pi,j)是以像元Pi,j为中心,以d为半径的不包含Pi,j的邻域窗口。如果窗口开的过小,包含的像元太少,噪音会对估计的结果产生严重的干扰;如果窗口开得过大,一些距离中心像元较远的像元与中心像元光谱相似性很小,会错误地低估像元的同质指数。地理学第一定律指出空间距离越近,像元的相关性越高,所以设计空间权重按照离窗口中心的距离衰减,这样距离中心较远的像元对应的权重较小,所以不论是否被包含在窗口内,对同质指数的影响较小。因此降低了同质指数对窗口大小的依赖[12]。很多文献中邻域窗口权重参数都随着距离的增加而降低,例如文献[22]中反比于距离,文献[22],[23]中反比于距离的平方,文献[14]通过高斯滤波函数体现空间邻域的权重对距离呈指数衰减。在距离较大的时候,指数比多项式衰减的更快。所以选择指数衰减的空间邻域权重可以减小距离较远且与中心像元光谱相似性较低的像元对同质指数错误地估计。定义ω如下式
在本文的空间同质分析中不妨设窗口半径d=2。光谱角距离[12, 19]是高光谱影像分析中最常用的光谱相似性测度,它对光谱的缩放变化具有不变性。本文选择光谱角距离的余弦值作为两个像元间的光谱相似性测度,令
 分别表示像元Pi,j和Pr,c的反射光谱。
分别表示像元Pi,j和Pr,c的反射光谱。
本文提出一种基于空间同质分析的稀疏解混算法(homogeneity analysis based SUnSAL-TV,SUnSAL-HTV)。首先进行影像空间同质分析,按照式(5)提取像元的同质指数,然后依据同质指数调整TV正则项权重。当hi很大时,表示像元与其邻近像元的光谱相似性很高,应该赋予较大的TV正则项权重,反之则赋予较小的权重。令 ),由于hi∈[m,1]比较小,对其作一个线性拉伸,将其变换到
),由于hi∈[m,1]比较小,对其作一个线性拉伸,将其变换到 ∈[1,M],令
∈[1,M],令 ,其中
,其中 。当hi(Pi,j)=1时,表示像元与其邻近像元之间的光谱完全一样,这时它们的地物丰度值也应该完全一样,应该赋予非常强的TV正则项权重,这里是M倍于同质指数最低的像元对应的TV正则项权重。参数M的取值会在试验部分详细地讨论。定义新的线性算子
。当hi(Pi,j)=1时,表示像元与其邻近像元之间的光谱完全一样,这时它们的地物丰度值也应该完全一样,应该赋予非常强的TV正则项权重,这里是M倍于同质指数最低的像元对应的TV正则项权重。参数M的取值会在试验部分详细地讨论。定义新的线性算子 和
和 如式(7)、(8)所示
如式(7)、(8)所示
在影像的右边和下面的边界处式(7)或(8)无法计算,这时令
 xi,j=0或
xi,j=0或 xi,j=0。 令
xi,j=0。 令 ,最后像元解混问题表示为求式(9)的最优化问题
,最后像元解混问题表示为求式(9)的最优化问题该优化问题可以基于ADMM策略迭代求解[18]。 4 试验与分析
因为真实的高光谱影像像元的组分和丰度信息难以获取,无法作定量分析,而模拟数据中像元的组分和丰度都是已知的,所以本文设计了一份模拟数据,定量地分析算法的解混精度。从USGS光谱库splib06(http://speclab.cr.usgs.gov/spectral.lib06)中提取498种地物光谱(每种地物光谱有224个波段)建立光谱库A∈R224×498。为了降低光谱库中端元的相干性,从A中提取子库A′,使得A′中每个端元之间的光谱角距离大于4.44°,A′∈R224×240。模拟数据由端元光谱库A′中随机选择的7个端元依据式(1)线性混合而成。为了验证同质分析在高光谱影像稀疏解混中的有效性,构造一份50×50个空间像元、224个波段的模拟数据。如图 1所示,该数据包含4个同质区,同质区之间是5个过渡区。同质区中像元含有的地物种类和对应的丰度完全相同;其中同质区1和4分别只含有一个端元,是纯净像元区;同质区2和3是同质的混合像元区,同质区2含有2个端元,它们对应的丰度分别为0.3和0.7,同质区3分别含有3个端元,它们对应的丰度分别为0.2、0.3和0.5。过渡区是不同的同质区地物的平滑过渡,所以设计过渡区包含有所有它相邻接的同质区域内的所有端元。令像元中端元的丰度x=e-d2xT,xT为端元对应同质区中端元的丰度,d是像元到此同质区的距离。影像中间的过渡区是像元混合最复杂的区域,称之为复杂混合区,与所有同质区相邻,像元的混合程度最高,包含所有的7个端元。以上构造的模拟数据覆盖了从纯净度最高的区域(1个端元)到混合度最高的区域(7个端元);既有地物丰度稳定的区域(同质区),也有地物丰度变化的区域(过渡区);既有纯净的同质区也有不同混合程度的同质区。并且由于TV正则项表示像元与水平和垂直邻接像元的丰度差值,在构造的模拟数据中,过渡区1和2中像元只有水平变化,过渡区3和4中像元只有垂直变化,过渡区5中像元既有水平变化也有垂直变化。所以模拟数据很好地包括了各种复杂的地物分布类型,而且非常适合检验SUnSAL-TV算法以及本文算法的解混效果。在高光谱影像中噪音大部分是低通的模型误差,因此通过对0均值的独立同分布高斯噪音进行低通滤波作为模拟数据的加性噪音[2, 18]。在本文的试验中对模拟数据分别加上20dB、30dB和40dB的加性噪音,来检验噪音对解混算法的影响。

|
| 图 1 模拟数据的同质区、过渡区和端元的空间分布示意图 Fig. 1 Homogeneous and transitional regions pattern and endmembers distribution map of simulated data |
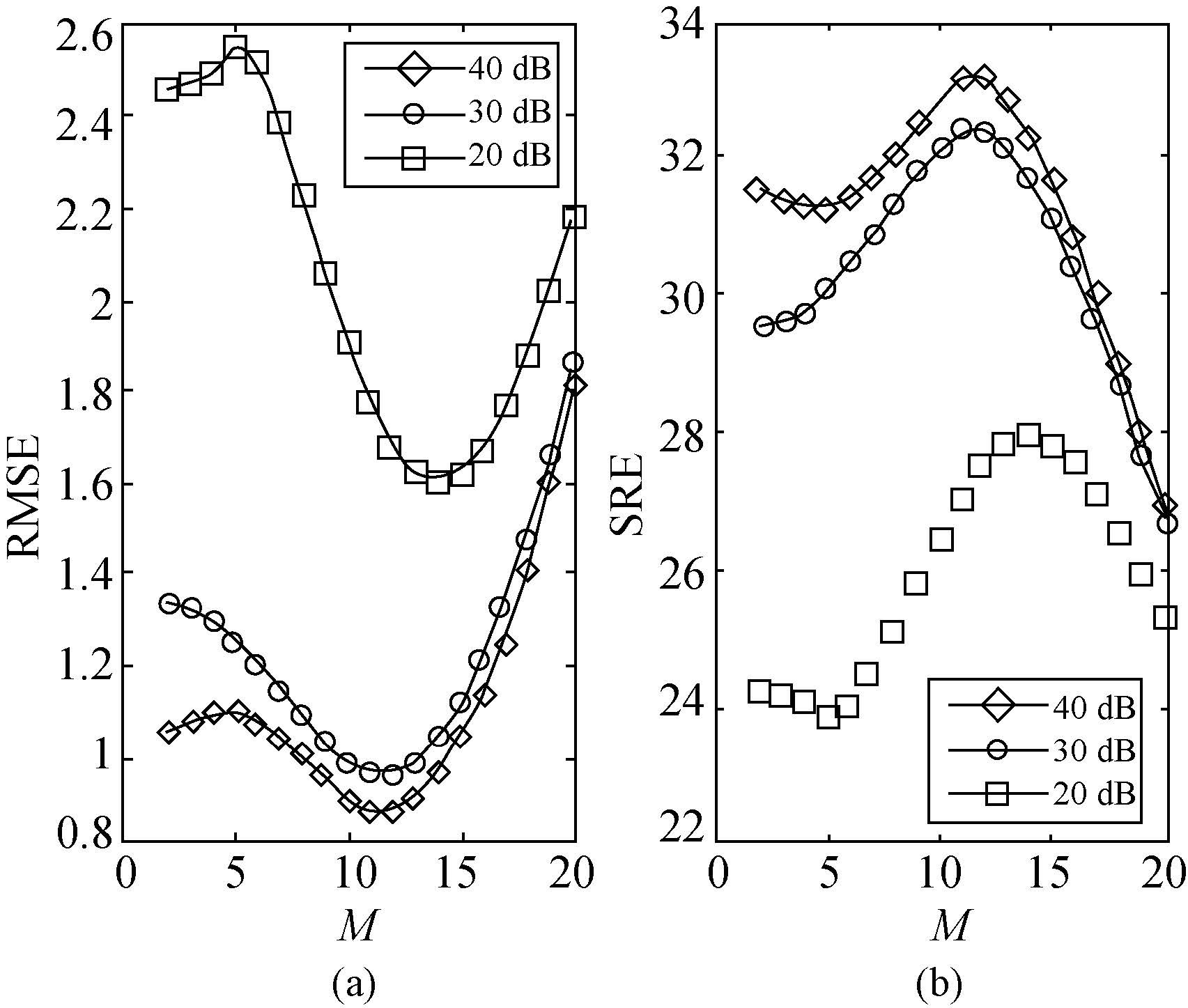
最常用的稀疏解混算法评价指标包括均方根误差(root mean square error,RMSE)和信号重构误差(signal to reconstruction error,SRE)[2, 18];RMSE的值越小,表示丰度的估计值越接近真实值,解混的精度越高;SRE是信号的能量与误差的能量的比值,能更好地度量解混精度,与RMSE相反,SRE的值越大,解混精度越高。文献[18]通过模拟数据的试验,详细讨论了稀疏约束项权重参数λ和TV正则项权重参数λTV在不同的噪音水平下和不同的解混算法下的最优取值,本文试验参考文献[18]中参数的取值,但是为了更直观地比较,在不同的噪音水平下,所有算法中都令权重λ=0.05,λTV=5×10-4,M=5。表 1显示了SUnSAL、SUnSAL-TV和SUnSAL-HTV算法在不同噪音水平下的解混精度。结果表明SUnSAL-TV要比SUnSAL的解混精度高,而SUnSAL-HTV在SUnSAL-TV的基础上进一步提高了解混精度(当噪音水平较高时精度提高明显,当噪音水平较低时SUnSAL-TV和SUnSAL-HTV解混精度很接近,RSME表示SUnSAL-TV精度稍高,SRE表示SUnSAL-HTV精度稍高);当噪音干扰变大时,以上算法的解混精度都会降低,但是SUnSAL-HTV的解混精度变化相对而言要小,即SUnSAL-HTV算法的抗噪性更好。进一步将同质区和过渡区的解混精度进行比较,表 2显示了噪音干扰最大(SNR=20dB)时的精度评价结果。结果表明同质区的解混精度高于过渡区,复杂混合区的解混精度最差(当SNR=30dB或者40dB时仍然得到相同的结论),所以在解混时应该对同质区和过渡区区别对待。参数M是最同质的像元和最不同质的像元赋予的TV正则项权重的比值,图 2显示了SUnSAL-HTV算法的解混精度在参数M为自变量下的变化情况。RMSE(图2(a) )和SRE(图 2(b) )同时指出:当噪音水平为40dB、30dB和20dB时,M值分别为11、12和13,SUnSAL-HTV算法的解混精度最高,即最优M值随着噪音水平的增加而递增。这表明在SUnSAL-HTV算法中对同质性高的像元赋予较大的权重能抑制噪音对解混精度的影响。
| 噪音 水平 /dB | SUnSAL | SUnSAL-TV | SUnSAL- HTV | |||||
| RSME | SRE | RSME | SRE | RSME | SRE | |||
| 20 | 0.2119 | 9.0713 | 0.2044 | 9.3052 | 0.2041 | 9.3240 | ||
| 30 | 0.2056 | 9.1805 | 0.2028 | 9.3428 | 0.2031 | 9.3457 | ||
| 40 | 0.2048 | 9.2028 | 0.2027 | 9.3452 | 0.2030 | 9.3475 | ||
| SUnSAL | SUnSAL-TV | SUnSAL- HTV | ||||||
| RSME | SRE | RSME | SRE | RSME | SRE | |||
| 同质区 | 0.2043 | 9.3817 | 0.1962 | 9.5966 | 0.1958 | 9.6146 | ||
| 过渡区 | 0.2246 | 8.4786 | 0.2199 | 8.7014 | 0.2197 | 8.7240 | ||
| 复杂区 | 0.2330 | 5.8654 | 0.2110 | 6.7150 | 0.2110 | 6.7127 | ||
|
| 图 2 同质尺度参数M对SUnSAL-HTV算法解混效果的影响 Fig. 2 Effect of the homogeneity scale parameter M on the performance of SUnSAL-HTV |
真实数据的试验虽然不能对解混算法进行定量化的评价,但是可以定性地反映算法在实际影像处理中的有效性,所以本文同时进行了真实数据的试验,从丰度稀疏性和空间平滑性的角度定性地验证算法的有效性。本试验使用的真实数据为公开的AVIRIS赤铜矿遥感影像数据(http://aviris.jpl.nasa.gov/html/aviris.freedata.html),有224个波段,被广泛地用于验证端元提取和混合像元分解算法的有效性。试验区的矿物信息已经被深入研究过,所有的端元都在USGS的光谱库splib06中。本试验选取了一个50×50像元的试验区,剔除低信噪比的波段,剩下188个波段,即Y∈R188×2500。选择A′作为稀疏解混的端元光谱库,对应选择188个波段。 文献[18]对该数据用SUnSAL和SUnSAL-TV算法进行解混,经验性地选择稀疏约束项权重参数λ和正则项权重参数λTV为:λ=λTV=10-3。本试验对真实数据同时使用SUnSAL、SUnSAL-TV和SUnSAL-HTV算法进行解混,算法中λ和λTV选择与文献[18]相同的权重参数。试验表明以上算法的解混结果都保持较高的稀疏性,并且与USGS提供的1995年矿物分类图(http://speclab.cr.usgs.gov/cuprite95.tgif.2.2um_map.gif)相符;SUnSAL算法的丰度空间分布平滑性很差,有很多散乱的孤立点;SUnSAL-TV算法加入了空间TV正则项约束,丰度的空间分布平滑性有明显提升,但是仍有少许孤立点;SUnSAL-HTV算法得到的丰度空间分布平滑性更好。
5 结 论针对高光谱遥感影像混合像元分解这一技术难题,本文提出一种基于空间同质分析的稀疏解混方法,通过对高光谱影像进行空间同质分析来提取同质指数,并结合稀疏解混模型中的空间正则项的权重来反映高光谱影像端元丰度分布的空间复杂性,实现对高光谱混合像元的有效分解。本文通过模拟数据和真实数据的试验和分析表明同质分析在影像解混中是一种很有效的工具,影像的空间同质性越高,稀疏解混的精度也越高;结合空间信息进行高光谱影像的稀疏解混能明显提高解混的精度,并且对噪音有一定的抑制作用。
| [1] | BIOUCAS D J M, PLAZA A, DOBIGEOON N, et al. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-based Approaches[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2): 354-379. |
| [2] | IORDACHE M D, BIOUCAS D J M, PLAZA A. Sparse Unmixing of Hyperspectral Data[J]. IEEE Transactions on Geoscience and Remote Sensing,2011,49(6): 2014-2039. |
| [3] | IORDACHE M D, BIOUCAS D J M, PLAZA A. Recent Developments in Sparse Hyperspectral Unmixing[C]//Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium.[S.l.]:IEEE, 2010: 1281-1284. |
| [4] | IORDACHE M D. A Sparse Regression Approach to Hyperspectral Unmixing[D]. Lisbon: Technical University of Lisbon, 2011. |
| [5] | IORDACHE M D, BIOUCAS D J M, PLAZA A. On the Use of Spectral Libraries to Perform Sparse Unmixing of Hyperspectral Data[C]//Proceedings of IEEE GRSS Workshop Hyperspectral Image Signal Process.: Evolution in Remote Sensing.[S.l.]:IEEE, 2010:1-4. |
| [6] | YANG Z Y. Blind Spectral Unmixing Based on Sparse Nonnegative Matrix Factorization[J].IEEE Transactions on Image Processing,2011,20(4): 1112-1125. |
| [7] | BRUCKSTEIN A M, ELAD, ZIBULEVSKY M. On the Uniqueness of Nonnegative Sparse Solutions to Underdetermined Systems of Equations[J]. IEEE Transactions on Information Theory, 2008,54(11): 4813-4820. |
| [8] | PLAZA A, MARTINEZ P. Spatial/Spectral Endmember Extraction by Multidimensional Morphological Operations[J]. IEEE Transactions on Geoscience and Remote Sensing,2002,40(9): 2025-2041. |
| [9] | PLAZA A, MARTINEZ P. A Quantitative and Comparative Analysis of Endmember Extraction Algorithms from Hyperspectral Data[J]. IEEE Transactions on Geoscience and Remote Sensing,2004, 42(3): 650-663. |
| [10] | ROGGE D M, RIVAED B. Integration of Spatial-spectral Information for the Improved Extraction of Endmembers[J]. Remote Sensing of Environment, 2007(110): 287-303. |
| [11] | MEI S H. Spatial Purity Based Endmember Extraction for Spectral Mixture Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing,2010,48(9): 3434-3445. |
| [12] | ZORTEA M, PLAZA A. Spatial Preprocessing for Endmember Extraction[J]. IEEE Transactions on Geoscience and Remote Sensing,2009,47(8): 2679-2693. |
| [13] | MARTIN G, PLAZA A. Region-based Spatial Preprocessing for Endmember Extraction and Spectral Unmixing[J]. IEEE Geoscience and Remote Sensing Letters,2011,8(4): 745-749. |
| [14] | MARTIN G, PLAZA A. Spatial-spectral Preprocessing Prior to Endmember Identification and Unmixing of Remotely Sensed Hyperspectral Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2): 380-395. |
| [15] | JIA S, QIAN Y T. Spectral and Spatial Complexity-based Hyperspectral Unmixing[J]. IEEE Transaction on Geoscience and Remote Sensing, 2007,45(12): 3867-3879. |
| [16] | JIA S, QIAN Y T. Constrained Nonnegative Matrix Factorization for Hyperspectral Unmixing[J]. IEEE Transaction on Geoscience and Remote Sensing, 2009,47(1): 161-173. |
| [17] | ECHES O, DOBIGEON N, TOURNERET J Y. Enhancing Hyperspectral Image Unmixing with Spatial Correlations[J]. IEEE Transaction on Geoscience and Remote Sensing, 2011, 49(11): 4239-4247. |
| [18] | IORDACHE M D, BIOUCAS D J M, PLAZA A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4484-4502. |
| [19] | KESHAVA N, MUSTARD J F. Spectral Unmixing[J]. IEEE Signal Processing Magazine, 2002,11(2):44-57. |
| [20] | ROGGE D M. Iterative Spectral Unmixing for Optimizing Per-pixel Endmember Sets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3725-3736. |
| [21] | PATI Y C, REZAHFAR R, KRISHNAPRASAD P. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition[C]//Proceedings of Asilomar Conference Signals, Systems and Computing.[S.l.]:ASSC, 2003: 1-10. |
| [22] | LI H L, ZHANG L P. A Hybrid Automatic Endmember Extraction Algorithm Based on a Local Window[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49 (11): 4223-4238. |
| [23] | HAN Wenchao, TIAN Qingjiu, LU Yingcheng. Spatial Attraction Algorithm for Sub-pixel Mapping of Multispectral Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 169-174.(韩文超,田庆久,陆应诚. 多光谱遥感影像亚像元定位的空间引力算法研究[J]. 测绘学报,2011,40(2): 169-174.) |