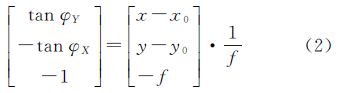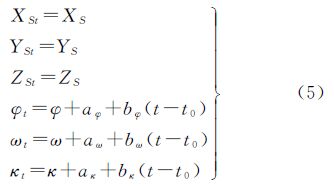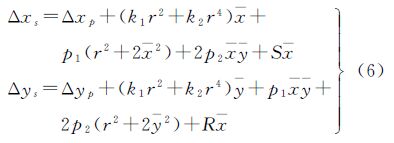随着卫星定姿、定轨以及传感器技术的发展,利用高分辨率卫星进行摄影测量已经成为一种重要的测绘手段。与航空摄影测量相比,卫星摄影测量具有可以对航空摄影测量困难区域(境外区域和环境恶劣区域)进行重复测绘的优势。近年来,随着高分辨率立体测绘卫星的陆续上天,我国也具备了对全球进行高精度测绘的条件。其中近期发射的资源三号卫星是我国首颗民用的三线阵高分辨率立体测绘卫星,其上装载有地面分辨率约为2 m的下视相机、地面分辨率约为3.6 m的前视和后视相机[1, 2]。通过卫星上搭载的GPS、星敏和陀螺设备获取卫星飞行时的位置和姿态,结合传感器等其他信息,可构建卫星影像的严格几何模型进行立体定位[3]。在实际应用中,立体定位受GPS、星敏和陀螺设备测量等误差的影响[4]。为了得到高精度的几何定位结果,一般需利用地面控制点对卫星影像进行区域网平差,以消除定位误差的影响[5, 6]。然而,卫星摄影测量具有飞行高度高、视场角小的特点,在平差时参数之间往往存在强相关性的问题,因此,选取合适的平差数学模型显得十分重要。
2 外方位元素计算的基本原理
根据附属文件提供的卫星成像时刻的位置和姿态,结合传感器信息,可由式(1)构建资源三号卫星影像的严格几何模型
式中,Xs、Ys、Zs为外方位线元素;m为尺度因子;RECIECR为空间固定惯性坐标系到地球固定参考坐标系的旋转矩阵;RbodyECI为本体坐标系到空间固定惯性坐标系的旋转矩阵;Rcamerabody为传感器坐标系到本体坐标系的旋转矩阵;φX和φY表示CCD像元在传感器坐标系中沿轨道方向和垂直于轨道方向的指向角[7]。φX和φY的计算公式为
式中,x、 y为像点坐标;x0、 y0为像主点坐标;f为相机主距。结合式(1)和式(2),可将资源三号卫星影像的严格几何模型转换为传统的共线条件方程 式中,Rij表示旋转矩阵R中第i行第j列的元素。旋转矩阵R的计算公式如下 由旋转矩阵R可计算外方位角元素φ、ω、κ。从而对影像上任意像点x、y均可计算一组外方位元素Xs、Ys、Zs、φ、ω、κ。 3 自检校光束法区域网平差 3.1 三线阵影像平差的轨道模型建立星载三线阵传感器轨道模型的目的是利用该模型描述传感器采样期间的位置和姿态变化。以此为基础进行光束法平差,可将平差目标从每个采样周期外方位元素的求解转化为求解轨道模型参数,从而减少未知数个数。常见的轨道模型有低阶多项式模型、分段多项式模型、定向片内插模型[8, 9]。
但在平差时,为减少未知数的个数和避免外方位线元素和角元素之间的相关性,可以根据实际情况对轨道模型进行优化。
在目前水平下,卫星定轨精度较高。资源三号卫星上搭载双频GPS,经精密定轨处理后定轨精度一般可达到厘米级。而目前国产卫星上搭载的星敏和陀螺设备的姿态测量精度一般为角秒级,在卫星飞行高度约为数百千米的情况下,对定位造成的误差影响还难以忽略[10, 11, 12]。因此,在实际定位时需采用一定的模型对其变化特征进行描述。
为避免线元素与角元素之间的强相关性,可将卫星定轨值当成真值,而只考虑卫星定姿误差的影响[13]。由于卫星在太空中飞行比较平稳,一般可采用低阶多项式模型对其姿态变化特征进行描述,其实质是对测姿系统的测量数据进行偏移和漂移误差改正。此时瞬时外方位元素XSt、YSt、ZSt、φt、ωt、κt可表示为[14]
式中,t0为起始时刻;XS、YS、ZS、φ、ω、κ为利用卫星辅助数据计算出的t时刻的外方位元素;aφ、aω、aκ为外方位角元素偏移改正量;bφ、bω、bκ为外方位角元素漂移改正量。 3.2 三线阵影像平差的附加参数模型三线阵相机的系统误差大体上可分为光学镜头误差和CCD线阵误差。与框幅式相机类似,三线阵相机的系统误差主要包括像主点的偏移、像元尺寸变化以及CCD旋转变化等误差。据此,附加参数模型构建如下[15, 16]
式中,Δxs和Δys为像点坐标的系统误差改正数;Δxp和Δyp为像主点偏移;k1和k2为径向畸变系数;p1和p2为偏心畸变系数;r为像点坐标到像主点的辐射距;x、y为像点坐标与像主点坐标的差值;S为比例尺因子;R为旋转因子。附加参数模型综合考虑了镜头光学畸变、像元尺寸变化和CCD旋转变化因素。但在具体的平差应用中,对于某一特定的区域网几何结构而言,附加参数的类型和个数会对法方程解算的稳定性产生影响[17, 18]。在平差中,为避免参数之间的强相关性问题,需对附加参数模型参数进行选择。
3.3 自检校光束法区域网平差模型在常规光束法平差的基础上[19],考虑轨道模型参数和附加模型参数,自检校光束法区域网平差的观测方程式可综合地写为[20]
式中,X为轨道模型参数向量;A为相应的系数矩阵;Y为附加模型参数向量;B为相应的系数矩阵;V为改正数向量;L为观测值向量。 4 试验与分析 4.1 试验数据本文的试验数据为河北安平地区和河南登封地区的资源三号影像、附属文件和控制点数据(图 1)。其中安平地区量测的控制点个数为70个,包括29个靶标控制点和41个自然地物控制点。但外业测量员将大部分控制点设在道路和农田的拐角处,由于部分拐角在全色影像上模糊难以判别,无法进行精确刺点。在删除识别不准的控制点后,最后得到64个控制点。登封地区虽有大量控制点,但这些控制点原本是为航空数据布设的,大量控制点在全色影像上无法判别。经过仔细判别,外业作业员共量测了12个控制点。安平地区的地形起伏较小,地貌以丘陵为主,区域内的地物包括河流、居民地和农田等。登封地区为山地,地形起伏较大。试验实施的平台为利用VC++ 6.0自行开发的软件SATT。

|
| 图 1 控制点分布图 Fig. 1 GCP distribution map |
选择不同的轨道模型、附加参数模型和控制点分布进行区域网平差试验。附加参数模型为Δxs、Δys、k1、k2、p1、p2、S、R时,选用不同的轨道模型,试验结果见表 1。轨道模型为姿态一阶时,选用不同的附加参数模型,试验结果见表 2。轨道模型为姿态一阶,附加参数模型为Δxs、Δys、p1、p2、 S、 R时,选用不同分布的控制点,试验结果见表 3。
| m | |||||||||
| 轨道模型 | 控制点 | 检查点 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | ||
| 姿态常数 | 1.286 | 1.255 | 1.797 | 1.721 | 1.521 | 1.641 | 2.237 | 1.835 | |
| 姿态一阶 | 1.170 | 1.230 | 1.698 | 1.651 | 1.334 | 1.747 | 2.198 | 1.769 | |
| m | |||||||||
| 附加参数模型 | 控制点 | 检查点 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | ||
| 未使用附加参数模型 | 8.365 | 12.861 | 15.342 | 5.789 | 5.599 | 8.506 | 10.183 | 6.392 | |
| Δxs、Δys、k1、k2、p1、p2、S、R | 1.014 | 1.315 | 1.661 | 1.430 | 2.039 | 1.839 | 2.746 | 1.857 | |
| Δxs、Δys、k1、k2、S、R | 2.358 | 1.725 | 2.922 | 1.688 | 1.916 | 1.800 | 2.628 | 2.055 | |
| Δxs、Δys、p1、p2、S、R | 1.170 | 1.230 | 1.698 | 1.651 | 1.334 | 1.747 | 2.198 | 1.769 | |
| Δxs、Δys、k1、p1、S、R | 1.084 | 1.275 | 1.674 | 1.848 | 1.385 | 1.657 | 2.160 | 2.466 | |
| Δxs、Δys、k1、p1、S | 0.972 | 1.283 | 1.610 | 2.262 | 1.678 | 1.673 | 2.370 | 3.153 | |
| Δxs、Δys、k1、p1、R | 2.123 | 1.742 | 2.746 | 1.884 | 2.753 | 2.454 | 3.688 | 2.570 | |
| Δxs、Δys、k1、S | 0.843 | 1.165 | 1.438 | 2.066 | 1.577 | 1.660 | 2.290 | 3.108 | |
| Δxs、Δys、k1、R | 2.233 | 1.707 | 2.810 | 1.621 | 2.854 | 2.340 | 3.691 | 2.496 | |
| Δxs、Δys、p1、S | 1.138 | 1.432 | 1.829 | 2.360 | 1.398 | 1.825 | 2.299 | 3.137 | |
| Δxs、Δys、p1、R | 5.218 | 2.251 | 5.683 | 2.098 | 3.954 | 2.173 | 4.512 | 2.535 | |
| Δxs、Δys,S、R | 1.005 | 1.201 | 1.566 | 1.894 | 1.404 | 1.688 | 2.196 | 2.773 | |
| Δxs、Δys、S | 1.047 | 1.330 | 1.693 | 2.155 | 1.433 | 1.774 | 2.281 | 3.078 | |
| Δxs、Δys、R | 5.198 | 2.135 | 5.620 | 1.970 | 3.919 | 2.109 | 4.450 | 2.522 | |
| Δxs、Δys | 8.800 | 2.978 | 9.290 | 2.205 | 6.353 | 2.754 | 6.924 | 3.298 | |
| m | |||||||||
| 控制点布设方案 | 控制点 | 检查点 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | ||
| 0.294 | 0.161 | 0.335 | 0.185 | 1.457 | 3.013 | 3.347 | 2.189 | ||
| 1.061 | 0.928 | 1.409 | 0.750 | 1.355 | 2.076 | 2.479 | 2.099 | ||
| 1.051 | 0.771 | 1.303 | 0.843 | 1.331 | 1.853 | 2.282 | 1.930 | ||
| 1.061 | 1.217 | 1.615 | 1.896 | 1.362 | 1.869 | 2.313 | 1.818 | ||
| 1.055 | 1.107 | 1.529 | 1.742 | 1.362 | 1.759 | 2.224 | 1.808 | ||
由表 1知,使用姿态常数的轨道模型,精度提高显著。当使用姿态一阶的轨道模型时,精度稍有提高。
由表 2知,使用不同的附加参数模型,平差精度也不同。不使用附加参数模型,平差精度相对较低。附加参数模型参数个数的增加并不一定能提高精度。参数个数太少时,平差精度也相对较差。这表明为了描述内方位元素的变化,需选用恰当的附加参数模型。从表 2知,附加参数模型为Δxs、Δys、p1、p2、S、R模型平差精度相对较为理想。为进一步验证附加参数模型Δxs、Δys、p1、p2、 S、 R在其他地区的适用性,采用登封地区的数据进行试验,自检校区域网平差后其平面精度约为2.074 m,高程精度约为1.737 m。安平地区和登封地区平差后的误差分布图如图 2所示。其中蓝色箭头表示高程误差,箭头指向误差方向;红色箭头表示平面误差,箭头指向误差方向。箭头方向向上表示误差为正,箭头方向向下表示误差为负。
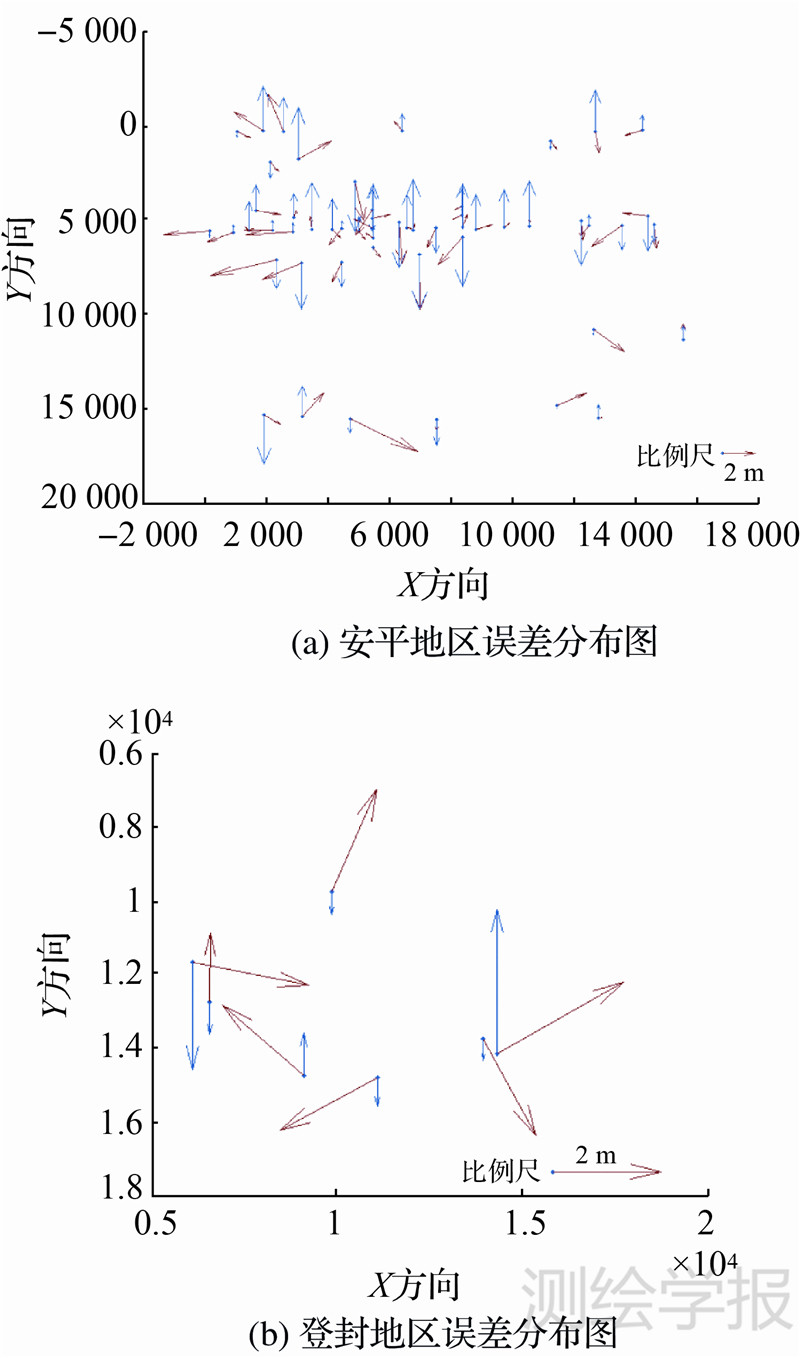
|
| 图 2 误差分布图 Fig. 2 Residual distribution map |
不同的控制点布设方案将会影响平差精度。采用四角点的布设方案时已经能达到较好的精度。在平差区域中心增加一个控制点时,平面精度有所改善,高程精度基本不变。随着控制点的增加,平面和高程精度均提高缓慢,当采用9点布设方案时,平面精度约为2.224 m,高程精度约为1.808 m。
5 结 论
本文对资源三号卫星三线阵影像平差所涉及的关于严格几何模型的构建、轨道模型的选择、附加参数模型的选择和控制点分布问题进行了全面的研究。试验表明,选择合理的轨道模型、附加参数模型和控制点分布,平差后平面精度约为0.6 GSD,高程精度优于0.5 GSD。本文的相关方法和结论可为我国航天三线阵影像的精密定位解算提供一定的技术参考。
| [1] | TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198.(唐新明,张过,祝小勇,等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报,2012,41(2): 191-198.) |
| [2] | LI Deren. China’s First Civilian Three Line Array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322.(李德仁. 我国第一颗民用三线阵立体测图卫星:资源三号卫星[J]. 测绘学报,2012,41(3):317-322.) |
| [3] | FAN Dazhao, LIU Chubin, WANG Tao, et al. Building& Validation of Rigorous Geometric Model of ALOS PRISM Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 569-574.(范大昭,刘楚斌,王涛,等. ALOS卫星PRISM影像严格几何模型的构建与验证[J]. 测绘学报,2011,40(5):569-574.) |
| [4] | WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42 (1): 1-5.(王任享,胡莘,王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报,2013,42(1):1-5.) |
| [5] | LIU Chubin, FAN Dazhao, WU Yongjin, et al. Self-Calibration Bundle Block Adjustment for ALOS PRISM Imagery[J]. Journal of Geomatics Science and Technology, 2012, 29(3): 196-199.(刘楚斌,范大昭,巫勇金,等. ALOS PRISM自检校光束法区域网平差研究[J]. 测绘科学技术学报,2012,29(3):196-199.) |
| [6] | ZHANG Guo, LI Deren, YUAN Xiuxiao, et al. The Mapping Accuracy of Satellite Imagery Block Adjustment[J]. Journal of Geomatics Science and Technology, 2006, 23(4): 239-241.(张过,李德仁,袁修孝,等. 卫星遥感影像的区域网平差成图精度[J]. 测绘科学技术学报,2006,23(4):239-241.) |
| [7] | National Centre for Space Studies. SPOT Satellite Geometry Handbook (S-NT-73-12-SI) [EB/OL]. [2006-10-8]. http://www.spotimage.fr/dimap/spec/documentation/refdoc.htm. |
| [8] | LEI Rong. Study on Theory and Algorithm of the In-flight Geometric Calibration of Spaceborne Linear Array Sensor[D]. Zhengzhou: Information Engineering University, 2011.(雷蓉.星载线阵传感器在轨几何定标的理论与算法研究[D]. 郑州:信息工程大学,2011.) |
| [9] | LIU Jun, WANG Donghong, LIU Jinxian, et al. IMU/DGPS Supported Block Adjustment of ADS40 Three Line Imagery Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 55-60.(刘军,王冬红,刘敬贤,等. IMU/DGPS系统辅助ADS40三线阵影像的区域网平差[J]. 测绘学报,2009,38(1):55-60.) |
| [10] | WANG Renxiang. Bundle Adjustment of Satellite Borne Three Line Array CCD Image[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 379-385.(王任享. 卫星三线阵CCD影像光束法平差研究[J]. 武汉大学学报:信息科学版,2003,28(4):379-385.) |
| [11] | YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41.(袁修孝,余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报,2008,37(1): 36-41.) |
| [12] | LIU Chubin, FAN Dazhao, WANG Tao, et al. Calibration of Constant Angular Error for ALOS PRISM Imagery[J]. Journal of Geomatics Science and Technology, 2011, 28(4): 278-283.(刘楚斌, 范大昭, 王涛,等. ALOS PRISM影像的姿态角常差检校[J]. 测绘科学技术学报, 2011, 28(4): 278-283.) |
| [13] | YUAN Xiuxiao, YU Xiang. Calibration of Angular Systematic Errors for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 42(3): 385-392.(袁修孝,余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报,2012,42(3): 385-392.) |
| [14] | KOCAMAN. Sensor Modeling and Validation for Linear Array Aerial and Satellite Imagery[D]. Zurich :ETH Zurich, 2008. |
| [15] | LIU Chubin. Study on Crucial Technique of the On-orbit Geometric Calibration of High Resolution Satellite[D]. Zhengzhou: Information Engineering University, 2012.(刘楚斌.高分辨率遥感卫星在轨几何定标关键技术研究[D]. 郑州:信息工程大学,2012.) |
| [16] | TANG Zhiqiang, FAN Dazhao, LIU Chubin, et al. Inner Orientation Modeling and Validation for Nadir Sensor of ALOS/PRISM[J]. Science of Surveying and Mapping, 2011, 36(6): 35-36.(汤志强,范大昭,刘楚斌,等. ALOS PRISM 下视传感器内方位分析与建模[J]. 测绘科学,2011,36(6):35-36.) |
| [17] | TANG Zhiqiang, SU Wenbo, GE Haijun. The Inner Orientation Modeling and Optimization of Space Line-array CCD Sensor[J]. Remote Sensing Information, 2010(6):3-5.(汤志强,苏文博,葛海军. 航天线阵CCD传感器内方位建模与优化[J]. 遥感信息,2010(6):3-5.) |
| [18] | GAN Tianhong, YAN Li. The Study of Ridge Estimation Based Decorrelation Method for Three Line Scanner CCD Images Exterior Orientation Elements[J]. Bulletin of Surveying and Mapping,2007(3): 19-22.(甘田红,闫利. 基于岭估计的三线阵CCD影像外方位元素去相关性方法研究[J]. 测绘通报,2007(3):19-22.) |
| [19] | WANG Zhizhuo. Photogrammetry Principle[M]. Wuhan: Publishing House of Wuhan University, 2007.(王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社,2007.) |
| [20] | LI Deren, ZHENG Zhaobao. Analytical Photogrammetry[M]. Beijing: Publishing House of Survey and Mapping, 1992.(李德仁,郑肇葆.解析摄影测量[M].北京:测绘出版社,1992.) |