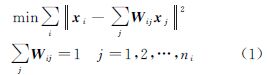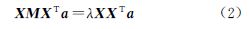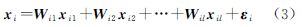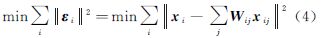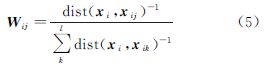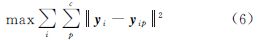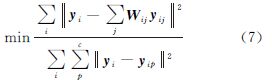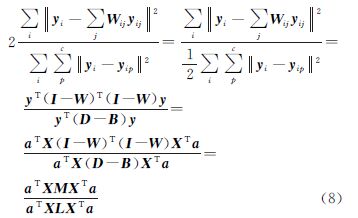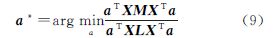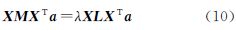1 引 言
随着遥感技术的不断发展，超光谱遥感图像数据的获取也变得越来越容易。超光谱遥感图像包含的光谱频带波段数量多，信息丰富，广泛应用于地表目标识别领域，如环境监测[1]、土地农作物分析[2]、气象分析[3]等。近年来，如何精确智能地区分超光谱地表遥感图像中不同种类的地物已成为一个新兴热门的研究领域，其面临的主要困难是图像分类时训练样本的数量有限，不能建立精确的分类器模型，且易产生Hughes 现象[4]。因而高维遥感图像特征提取算法研究引起了广泛的兴趣并获得了快速发展，如log Gabor滤波器[5]、基于融合点云的特征提取法[6]。图像特征提取在降维的同时还能够保留图像尽可能多的信息[7]，有利于后续的图像处理。
主成分分析(principal component analysis，PCA)[8]是一种无监督特征提取算法，并广泛用于遥感图像处理[9]。它通过分析原始数据的协方差矩阵来进行特征提取，协方差矩阵的特征值大小代表信息量的多少，特征值较大代表有用信息，较小特征值代表的可能是噪声信息。但是作为一种无监督特征提取算法，PCA不能较好地利用类别标签信息。线性判别分析(linear discriminant analysis,LDA)和非参数权重特征提取(nonparametric weighted feature extraction，NWFE)是广泛用于遥感图像的两种有监督降维方法，它们找到一个最优投影矩阵，在投影子空间中最大化类内散度矩阵的迹同时最小化类间散度矩阵的迹。近几年，这两种算法得到不断地扩展，如：改进的Fisher线性判别分析、正则线性判别分析[10, 11, 12, 13]等等。然而，这些算法只注重全域欧几里德结构而忽略了高维遥感数据的局部空间结构信息。
对于小样本问题，可运用线性化来构建邻域结构图进行特征提取，如有监督局部保留投影(supervised locality preserving projection，SLPP)[14] —Laplacian eigenmaps(LE)[15]的线性化,邻域保留嵌入(neighborhood preserving embedding，NPE)[16]—局部线性嵌入(locally linear embedding，LLE)[17]的线性化。SLPP能够保留样本固有的局部流形结构不变，利用局部结构信息和全域标签信息，构造邻域相似性矩阵和类相关矩阵，根据使投影后的同类像素点之间的距离尽可能小的目标，利用求最优解方法求得最优投影矩阵。因此，SLPP能把同类像素点尽可能投影在一起，把不同类的像素点尽可能分开。NPE利用局部邻域点信息，每个像素点可以被周围几个像素点线性表示，各权重系数由与目标像素点的距离决定。由此可以找到一个最优邻域嵌入映射矩阵，使得在低维空间中邻域信息得到很好的保留。然而，对于分类问题，NPE忽略了同类与非同类样本的差异。
本文在NPE基础上，提出了一种算法，名为判别监督邻域保留嵌入(DSNPE)特征提取算法。DSNPE算法中，每个像素点由邻域中的同类像素点线性表示，而不是所有邻域中的像素点，这与SLPP算法构造相似性矩阵和类相关矩阵的方式完全不同。同时在所投影的低维空间中，DSNPE能使非同类的像素点之间尽可能离得远。DSNPE主要有三大优点：①算法同时考虑了类内结构和类间结构，使分类时效果更好；②考虑了邻域点中同类样本与非同类样本的区别，使可判别性更高；③在低维空间中，能使同类样本离得更近而非同类样本离得更远。
2 邻域保留嵌入算法(NPE)设X=[x1,x2,…,xN]为一组高维原始数据向量集，其中{x1,x2,…,xN}∈Rn，Y=[y1,y2,…,yN] 表示与高维原始数据映射对应的低维空间向量集，{y1,y2,…,yN}∈Rd，(d«n)，n表示遥感图像光谱波段数，d表示特征提取后特征空间的维数，N表示样本总数。特征提取的目标是找到一个n×d的投影矩阵A，使每一个原始数据点xi都能通过yi=AxiT，映射到另一特征空间，并且保留高维数据的绝大部分信息。
NPE算法中每个像素点可由其邻域点线性表示，建构邻域结构连接图，表示其邻域信息。某些情况下，局部子流形结构是非线性的，可以将其近似线性化。假设xi表示第i个像素点，如xj在xi的邻域内，则将他们连接起来，构建邻域结构图，用矩阵W来表示邻域结构图连接权重，Wij表示点xj到点xi的权重，若Wij值为0则表示xj不在点xi的邻域内。权重系数可以通过求解最小化目标方程(式(1))求取 然后求解广义特征根方程(式(2))得出转换矩阵A 式中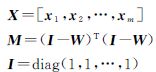
可以看出M是对称矩阵且半正定，设列向量a1、a2、…、ad为方程(2)的解，它们对应的特征值分别为λ1、λ2、…、λd，且λ1≤λ2≤…≤λd，则嵌入公式如下
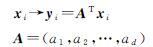式中，yi是d维向量；A是n×d矩阵。
与NPE算法不同，DSNPE算法中每个像素点由邻域中的同类像素点线性表示，而非所有像素点，即像素点xi由xi1、xi2、…、xil线性表示，xi1、xi2、…、xil与xi属于同一类，且都属于xi的K个最近邻域点，表示如下
式中，εi是线性重构误差。最小化误差的平方有
为了突出邻近点重要性，本文权重系数的计算采用邻域像素点与xi的距离倒数计算出来，dist(a,b)即表示a到b的距离，假如xij与xi的距离越近，倒数越大，它的权重就越大，接近于1，否则权重越小，接近于0，其他非邻域像素点xj，Wij=0。设Y=[y1y2…ym]T为映射后的低维空间中的点集，则可以推出下列最小化目标方程
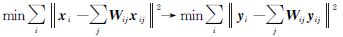
同时，设yi1、yi2、…、yic(c=k－l)为yi非同类映射点，为了使非同类点离得尽可能远，可以最大化yi与yi1、yi2、…、yic距离之和，则有
结合式(4)和式(6)，两最优化问题可以转化为下面比例最优求解问题
因为yT=aTX为线性变换，xi为X的第i列向量，则有 式中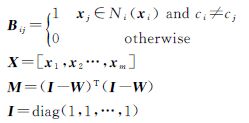
D为对称矩阵，其元素是B的列(或行)之和，
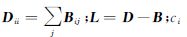表示xi的类别；Ni(xi)表示xi的最近k个邻域点。简化目标方程如下
设转换向量为目标方程的特征向量解，则式(9)可以转化为下列广义特征值求解问题
最后求得转换矩阵A=[a1,a2,…,ad]，xi→yi=AxiT。
4 试验设计本文采用美国Indian Pine、 KSC 和Washington DC Mall 3幅超光谱遥感图像作为试验对象，选择PCA、NWFE、LPP和NPE 4种有代表性的特征提取算法与DSNPE进行对比。试验过程是先用这5种特征提取算法对原始图像进行特征提取，然后在相同条件下采用相同分类器进行分类，比较分类效果，即总体分类正确率和Kappa 系数。分类器选取最近邻分类器。
4.1 试验对象试验对象假彩色图像如图 1所示。
|
| 图 1 试验对象假彩色图 Fig. 1 Simulated grayscale IR image for experiment |
(1) 图像India Pine拍摄对象是Indian Pine的西北部部分区域的光谱图像[15]，地面空间分辨率为18m，大小是145像素×145像素，此图含有220个波段，通过去除噪声通道频带后保留了185个波段，覆盖的波长范围是0.4～2.4μm。此区域所含类别数为16，为了方便试验，本文选取了其中样本数超过100的13类(见表 1)，试验样本总数为10221。此图更详细资料参见文献[18]。
| India Pine | KSC | DC Mall | |||||
| 类别 | 类名(数量) | 类别 | 类名(数量) | 类别 | 类名(数量) | ||
| 1 | 玉米1(1434) | 1 | 灌木(761) | 1 | 屋顶(2685) | ||
| 2 | 玉米2(834) | 2 | 柳树沼泽(243) | 2 | 街道(416) | ||
| 3 | 玉米3(234) | 3 | 棕榈小丘(256) | 3 | 小路(175) | ||
| 4 | 大豆1(968) | 4 | 橡木小丘1(252) | 4 | 草地(418) | ||
| 5 | 大豆2(2468) | 5 | 橡木小丘2(229) | 5 | 绿树(405) | ||
| 6 | 大豆3(614) | 6 | 沼泽松(161) | 6 | 水(449) | ||
| 7 | 牧场1(497) | 7 | 双子叶树(105) | ||||
| 8 | 牧场2(747) | 8 | 禾草沼泽(431) | ||||
| 9 | 牧场3(26) | 9 | 大米草沼泽(520) | ||||
| 10 | 干草(489) | 10 | 香蒲沼泽(404) | ||||
| 11 | 小麦(212) | 11 | 盐沼(419) | ||||
| 12 | 乔木(1294) | 12 | 泥滩(503) | ||||
| 13 | 木屋(380) | 13 | 水(927) | ||||
(2) 图像KSC 是在肯尼迪太空中心拍摄佛罗里达州的超光谱图像，地面空间分辨率为18m，含有224个波段，去除噪声通道频带后保留了176个波段，覆盖的波长范围是0.4～2.4μm。本文截取512像素×614像素大小的区域进行试验。此区域所含类别数为13(见表 1)，试验样本总数为5211。此图更详细信息参见文献[19]和http://www.csr.utexas.edu网站。
(3) 图像DC Mall 拍摄对象是美国华盛顿城市的一片区域[16]，地面空间分辨率为18m，大小是1280像素×307像素，去掉噪声通道频带后保留了191个波段，覆盖的波长范围是0.4～2.4μm。本文选取了550像素×307像素大小的区域进行试验。这个区域所含类别数为7，选取其中样本数超过100的6类(见表 1)，试验样本总数为4452。此图更详细信息参见文献[20]。
4.2 试验结果及分析为了探索各种特征提取算法的效果，本文选取了3组不同训练样本数目进行试验，训练样本的数量为在每类中随机分别选取20、40、100。试验时，选取一定比例的样本作为训练样本，其他样本作为测试样本。因为各试验图像所含类别数不同，分别为13、13和6，所以提取的最大特征数分别设置为20、20和15。试验重复10次，平均值作为最终试验结果。
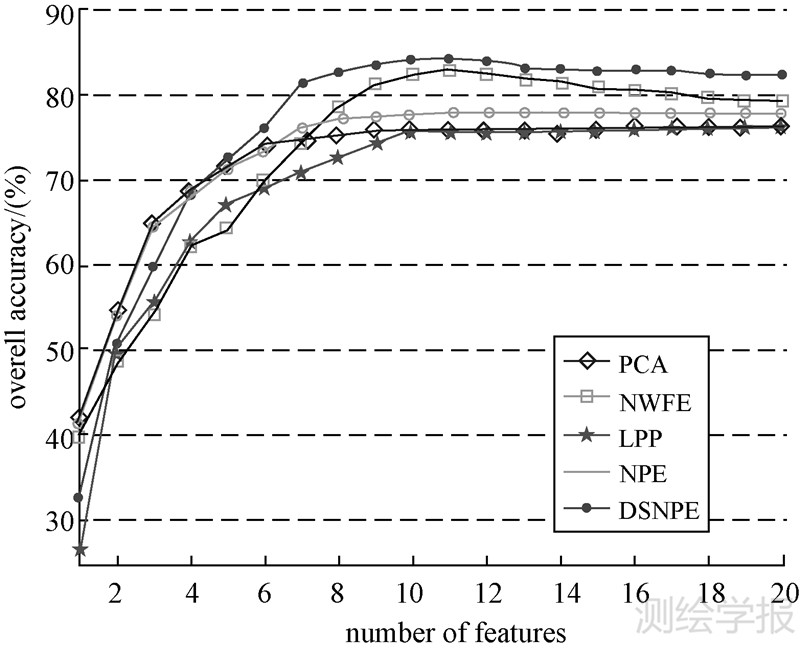
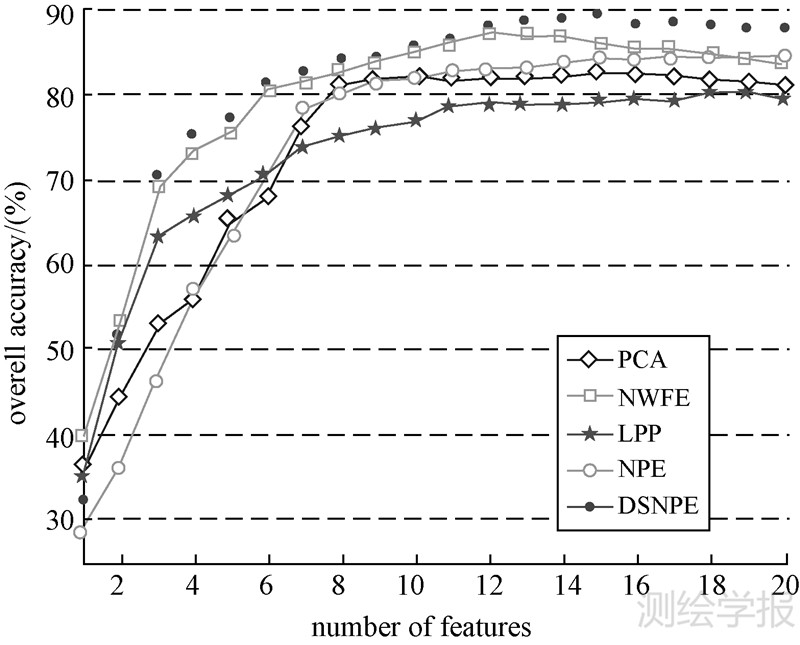
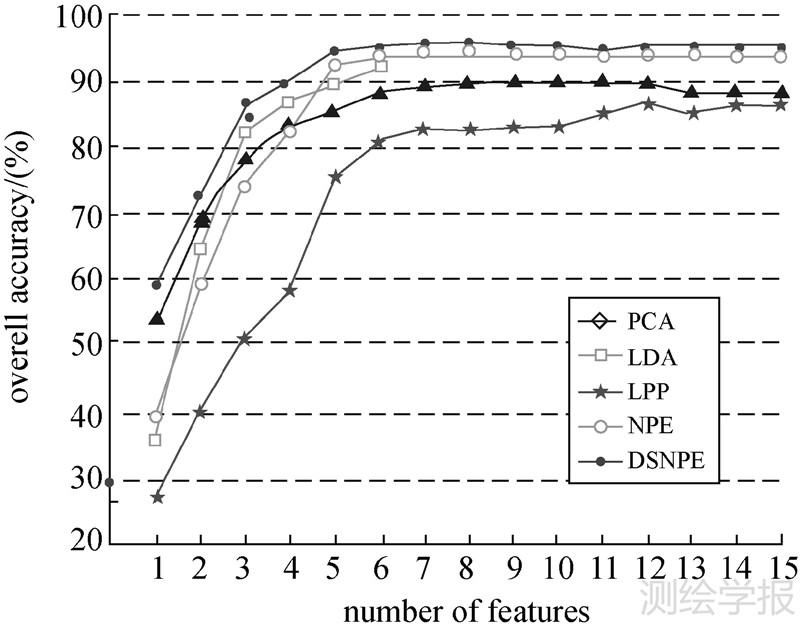
试验结果见图 2-图 4和表 2。图 2—图 4是当训练样本数量不变时，平均分类正确率随着提取特征数的不断增长而变化的曲线图；表 2的数据是指最高平均分类正确率(对应的特征数)和Kappa系数。通过DSNPE和其他几种算法对遥感图像Indian Pine特征提取后，分类结果如图 5所示。分析上述结果可以得到以下几点：
|
| 图 2 Indian Pines分类平均正确率曲线图 Fig. 2 Curves of average classification accuracies for Indian Pine (Ni=100) |
|
| 图 3 KSC分类平均正确率曲线图 Fig. 3 Curves of average classification accuracies for KSC (Ni=100) |
|
| 图 4 DC mall分类平均正确率曲线图 Fig. 4 Curves of average classification accuracies for DC mall (Ni=100) |
| 对象 | 样本数目 | 算法 | PCA | NWEF | LPP | NPE | DSNPE |
| IndiaPine | 20 | OA | 64.6(11) | 68.1(13) | 53.1(19) | 63.1(17) | 66.1(17) |
| k | 59.8 | 64.4 | 48.1 | 58.4 | 61.5 | ||
| 40 | OA | 69.1(13) | 73.8(11) | 64.1(14) | 70.4(15) | 75.0(11) | |
| k | 65.5 | 70.4 | 60.2 | 67.0 | 71.8 | ||
| 100 | OA | 76.2(16) | 82.9(11) | 76.0(18) | 77.8(17) | 84.3(11) | |
| k | 73.4 | 81.0 | 73.1 | 75.1 | 82.4 | ||
| KSC | 20 | OA | 69.6(17) | 67.7(9) | 55.1(17) | 54.8(15) | 68.9(15) |
| k | 67.7 | 65.8 | 51.5 | 52.7 | 67.3 | ||
| 40 | OA | 80.5(17) | 82.6(12) | 68.0(16) | 79.3(16) | 83.9(15) | |
| k | 72.3 | 80.5 | 65.7 | 77.1 | 81.9 | ||
| 100 | OA | 82.4(18) | 87.4(12) | 80.2(19) | 84.3(16) | 89.4(15 | |
| k | 80.5 | 86.0 | 78.5 | 83.1 | 88.1 | ||
| DC mall | 20 | OA | 77.5(9) | 81.9(4) | 64.4(11) | 81.3(7) | 82.2(5) |
| k | 66.1 | 71.8 | 51.2 | 69.5 | 72.0 | ||
| 40 | OA | 86.4 (9) | 87.5(6) | 81.7(10) | 87.2(6) | 88.9(8) | |
| k | 79.2 | 79.9 | 69.8 | 79.8 | 80.7 | ||
| 100 | OA | 89.8(10) | 94.0(6) | 86.5(11) | 92.1(7) | 95.7(7) | |
| k | 81.5 | 88.6 | 79.1 | 85.6 | 90.4 |
|
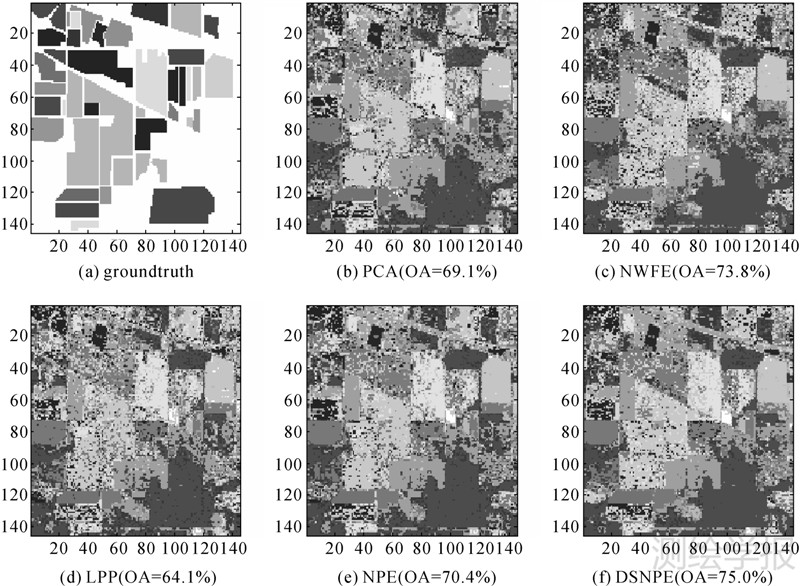
| 图 5 Indian Pine 分类效果图(Ni=40) Fig. 5 Classification maps for Indian Pine (Ni=40) |
(1) 与其他几种特征提取算法相比，DSNPE分类效果最好，分类正确率最高。
(2) 与NPE相比，DSNPE不仅仅考虑到类内样本与类间样本的区别，还加入了类间样本的判别信息，使不同类样本之间离得尽可能远，因此分类效果得到了提高。
(3) 随着提取特征数的增加，NWFE的分类正确率上升到一定程度后开始下降，而DSNPE不会下降。
(4) DSNPE分类效果同样好于PCA和LPP，说明DSNPE提取的特征更具判别性。
5 结 论本文提出了一种判别监督邻域保留嵌入(DSNPE)超光谱遥感图像特征提取算法。该算法充分利用训练样本的标签信息，在目标样本线性化表示时选择邻域中同类样本而不是邻域中所有样本，并且将邻域中同类和非同类像素点分开处理，利用判别分式求解最优投影矩阵，使高维像素点投影到低维空间时，同类点离得尽可能近，非同类点离得尽可能远。与PCA、NWFE、LPP和NPE等特征提取算法的对比试验也说明DSNPE有一定的优越性，提取的特征判别性更强，使分类正确率得到提高。
| [1] | AGYEMANG T K, HEBLINSKI J. Accuracy Assessment of Supervised Classification of Submersed Macrophytes: The Case of the Gavaraget Region of Lake Sevan, Armenia[J]. Hydrobiologia, 2011, 661(1): 85-96. |
| [2] | TRACOL Y, GUTIERREZ J R. Plant Area Index and Microclimate underneath Shrub Species from a Chilean Semiarid Community[J]. Journal of Arid Environments, 2011, 75(1): 1-6. |
| [3] | TOMLINSON C J, CHAPMAN L. Remote Sensing Land Surface Temperature for Meteorology and Climatology: A Review[J]. Meteorological Applications, 2011, 18(3): 296-306. |
| [4] | HUGHES G F. On the Mean Accuracy of Statistical Pattern Recognizers[J]. IEEE Transactions on Information Theory, 1968, 14(1): 55-63. |
| [5] | XIAO Pengfeng, FENG Xuezhi. Segmentation of High-resolution Remotely Sensed Imagery Based on Features in Frequency Domain[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 401-409. (肖鹏峰,冯学智. 高分辨率遥感图像频域特征提取与图像分割研究[J]. 测绘学报,2008, 37(3): 401-409.) |
| [6] | WU Hangbin. Classification and Feature Extraction of Airborne LiDAR Data Fused with Aerial Image[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):134-140. (吴杭彬. 融合航空影像的机载激光扫描数据分类与特征提取[J]. 测绘学报, 2011, 40(1): 134-140.) |
| [7] | FONG M. Dimension Reduction on Hyperspectral Images[R]. Los Angeles: University of California, 2007. |
| [8] | SCHOTT J. Remote Sensing: The Image Chain Approach[M]. Oxford: Oxford University Press, 1996. |
| [9] | FAUVEL M, CHANUSSOT J, BENEDIKTSSON J A. Kernel Principal Component Analysis for the Classification of Hyperspectral Remote-sensing Data over Urban Areas[J]. EURASIP Journal on Advances in Signal Processing, 2009, 2009(3): 1-15. |
| [10] | DU Q. Modified Fisher’s Linear Discriminant Analysis for Hyperspectral Imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(4): 503-507. |
| [11] | BANDOS T V, BRUZZONE L, CAMPS-VALLS G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis [J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47 (3): 862-873. |
| [12] | YANG J M, YU P T, KUO B C. A Nonparametric Feature Extraction and Its Application to Nearest Neighbor Classification for Hyperspectral Image Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1279-1293. |
| [13] | HUANG H Y, KUO B C. Double Nearest Proportion Feature Extraction for Hyperspectral-image Classi-fication[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(11): 4034-4046. |
| [14] | LUO Renbo, PI Youguo, LIAO Wenzhi. Research on Supervised LPP Feature Extraction for Hyperspectral Image[J]. Remote Sensing Technology and Application, 2012, 27(6): 46-52. (骆仁波,皮佑国,廖文志. 超光谱遥感图像有监督LPP特征提取研究[J]. 遥感技术与应用,2012, 27(6): 46-52.) |
| [15] | HE X F, CAI D, YAN S C, et al. Neighborhood Preserving Embedding[C]//Proceedings of IEEE 2005 International Conference on Computer Vision. Beijing: IEEE, 2005: 1208-1213. |
| [16] | BELKIN M, NIYOGI P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering[C]//Advances in Neural Information Processing System: 14. Cambridge: MIT Press, 2002: 585-591. |
| [17] | ROWEIS S T, SAUL L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290 (5500): 2323-2326. |
| [18] | University of Texas at Austin. AVIRIS NW Indiana’s Indian Pines 1992 Data Set[EB/OL]. Texas: University of Texas at Austin, 1992[2013-02-23]. ftp://ftp.ecn.purdue.edu /biehl/MultiSpec/92AV3C . |
| [19] | HAM J, YANGCHI C, CRAWFORD M, et al. Investigation of the Random Forest Framework for Classification of Hyperspectral Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 492-501. |
| [20] | LANDGREBE D A. Signal Theory Methods in Multispectral Remote Sensing[M]. Hoboken: Wiley, 2003. |