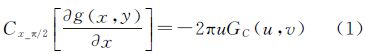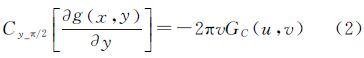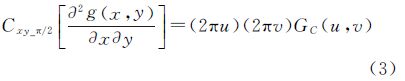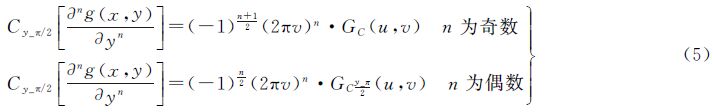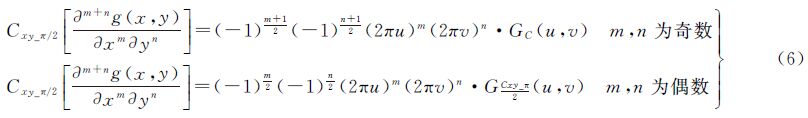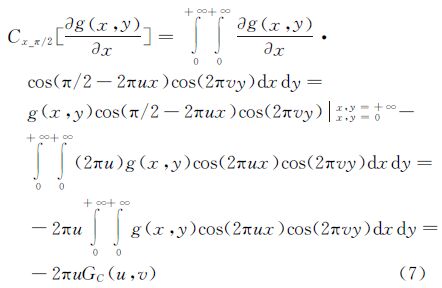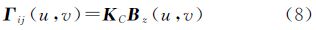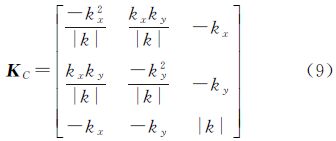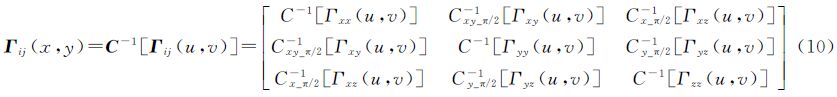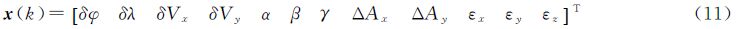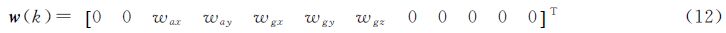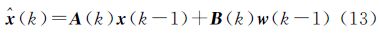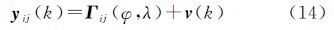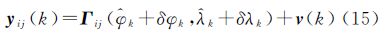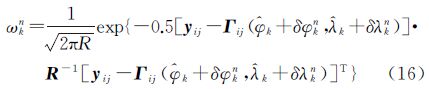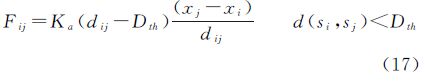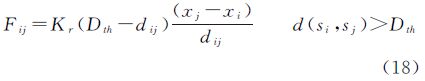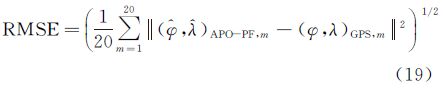2. 中国西南电子技术研究所,四川 成都 610036
2. Southwest China Institute of Electronic Technology,Chengdu 610036,China
1 引 言
惯性导航属于自主式无源导航,具有完全独立特性,不受任何自然条件或环境干扰的影响,具有全天候、全地域连续工作的特点[1]。然而惯性导航系统中由于存在惯性测量元件误差,如陀螺漂移和加速度计零位误差的存在,导致系统输出的载体姿态、速度和位置误差随时间而积累,难以满足长时间高精度导航定位的要求。
通常采用其他辅助导航方法与惯性导航系统相结合,以克服纯惯导系统的不足,但仍存在一些缺陷。如GPS和无线电导航不是自主式导航,易受人为干扰和电子欺骗,从而完全丧失导航能力[2, 3]。地形匹配和图像匹配导航对地形起伏特性有特殊要求,长时间跨水域、平原地带时,其灰度、纹理及地形等没有显著特征,匹配的精度和匹配概率受到明显制约,因此限制此类辅助导航方法使用的灵活性[4, 5, 6]。
地磁场属于地球空间环境物理场要素之一,是由不同变化规律的磁场成分叠加而成的矢量场,在地球近地空间内任意一点的磁场矢量都与其所处的经纬度和距离地心高度相对应,为导航系统提供了天然坐标系[7, 8]。因此利用地磁场矢量数据的惯性/地磁组合导航研究早已成为热点问题[9, 10, 11]。21世纪后,随着航空地磁场矢量梯度测量技术出现,由于其测量数据基本不受日变和正常场等因素的影响,同时具有较高的精度和分辨率,使得地磁梯度日益受到重视[12, 13]。因而以全张量地磁梯度测量数据为主的辅助导航方法将成为惯性/地磁组合导航研究发展的一个趋势和方向。
然而全张量地磁梯度测量刚刚步入标准化勘探阶段,通过航空磁力梯度测量实现大范围梯度数据库的构建,仍需要漫长的过程[14, 15]。因此本文研究利用现已广泛测量获得的磁场矢量分量数据,研究快速计算全张量地磁梯度数据的方法,并通过仿真试验分析惯性/地磁梯度组合导航系统的可行性。
2 基于余弦变换的全张量地磁梯度计算方法惯性/地磁梯度组合导航系统是一种新兴的辅助导航方法,是利用实时测量的地磁场梯度分量信息与存储的导航基准梯度图进行匹配定位,对惯导系统的累积误差进行修正,从而提高导航系统的精度。然而实际应用中由于实测地磁梯度数据缺乏,研究如何利用现已广泛开展测量获得的地磁场分量数据,通过位场导数转换方法计算全张量磁梯度分量已成为亟需解决的问题。
2.1 移相π/2二维余弦变换时域微分公式快速傅里叶变换是位场导数计算常用的频域方法,但存在Gibbs边界效应的缺点,而离散余弦变换最先应用于重力位场导数计算中,但由于没有给出各种移相π/2的连续余弦变换定义,缺乏对导数公式的理论推导证明[16]。因此通过对余弦变换理论进行深入研究,提出了分别在x、y方向上移相π/2的二维连续余弦变换定义,并进一步完善基于余弦变换的位场导数计算理论[17]。
基于傅里叶变换和余弦变换的频域导数计算方法,其理论基础都是依据时域微分公式将时域中变量之间的导数关系转换为频域中的乘积关系。因此下面给出移相π/2余弦变换一阶时域微分定义。
定义1:若二元函数g(x,y)、∂g(x,y)/∂x和∂g(x,y)/∂y在x,y∈[0,∞)定义区间满足傅里叶积分收敛条件,且当|x|→∞,|y|→∞时,二元函数g(x,y)→0,根据分别在x、y方向上移相π/2,以及同时在x和y方向上移相π/2的二维余弦变换定义,则存在以下公式成立
可以推导出任意阶余弦变换时域微分定义如下。
定义2:对任意整数m、n,若二元函数g(x,y)和∂j+kg(x,y)/∂xj∂yk,∂jg(x,y)/∂xj,∂kg(x,y)/∂yk,j=1,2,…,m;k=1,2,…,n都存在二维傅里叶变换,且当|x|→∞,|y|→∞时,二元函数g(x,y)→0,∂j+k-2g(x,y)/∂xj-1∂yk-1→0,∂j-1g(x,y)/∂xj-1→0,∂k-1g(x,y)/∂yk-1→0,则有
式中,u、v分别是在x、y方向上的空间频率;GC(u,v)为函数g(x,y)的二维余弦频谱密度函数;同理GCx_π/2(u,v)和GCy_π/2(u,v)为函数g(x,y)在x、y方向上分别移相π/2的余弦频谱密度函数;GCxy_π/2(u,v)为函数g(x,y)在x、y方向上同时移相π/2的余弦频谱密度函数。
定义1和定义2组成了完整的余弦变换时域微分定义。通过文献[17]中定义的在x、y方向上移相π/2的二维连续余弦变换,可以推导证明出移相π/2余弦变换时域微分定义如下
证明 :由在x方向上移相π/2的连续余弦变换定义,并利用分部积分,且存在 g(x,y)=0,可得
g(x,y)=0,可得
移相π/2的余弦变换时域微分定理中公式(1)得证,其余公式同理可证。
2.2 基于余弦变换的磁异常导数计算方法根据移相π/2的余弦变换时域微分定义,并将其与地磁场理论相结合,可推导出全张量磁梯度各个分量的计算公式。因此与傅里叶变换导数计算方法相似[18],可得由磁场垂向分量计算全张量磁梯度的余弦变换频率域数学模型,将其推导结果写为矩阵形式如下
式中,Bz(u,v)为磁场垂向分量Bz(x,y)的二维离散余弦变换,x、y为水平坐标;Γij分别对应各自方向的梯度分量,且有余弦变换导数计算系数矩阵KC为
式中,kx、ky为x、y方向上波数,kx=2πu,ky=2πv;波数|k|=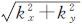 。
。
对频域导数计算公式(8)进行移相π/2二维余弦变换的逆变换,可进一步得到全张量梯度数据的空间域结果
因此,利用在导航区域内已经精确测量获得的地磁场分量数据,通过上文推导得出的磁场梯度分量计算公式,可实现高精度全张量磁梯度导航基准图数据库的构建,为在之前没有经过航磁梯度测量的区域内进行惯性/地磁梯度组合导航提供了必要的前提条件。
3 惯性/地磁梯度组合导航算法 3.1 辅助导航系统状态方程和量测方程根据捷联惯导系统的位置误差方程、速度误差方程和姿态角误差方程,选取惯性/地磁梯度组合导航系统的状态向量x(k)和系统噪声w(k)分别为
状态向量中,δφ和δλ为经纬度误差,ΔVx和ΔVy为东向和北向速度误差,α、β和γ分别为水平误差角和方位误差角,ΔAx和ΔAy为加速度计零位误差,εx、εy和εz分别为东向、北向和天向常值陀螺漂移。系统噪声中,wax、way、wgx、wgy和wgz均为零均值的高斯白噪声,分别对应加速度计零位漂移和陀螺随机漂移。
则根据文献[19]中确定的系统状态转移矩阵A(k)以及单位阵B(k)=I12×12可知全张量地磁梯度辅助导航系统滤波模型的系统状态方程为
惯性/地磁梯度组合导航通过相关匹配或滤波的方式,将实时测量地磁梯度分量与预先获得的梯度基准图相匹配,估计载体最佳位置。全张量磁梯度包含Γxx、Γyy、Γzz、Γxy、Γxz和Γyz 6个梯度分量,通过全张量磁力梯度仪对其进行实时测量,并作为组合导航系统的观测量。由于观测维数增多,可提高系统的导航定位精度,因此地磁梯度辅助定位系统量测方程可表示如下
式中,yij(k)为地磁梯度分量观测值,i,j=x,y,z表示空间方向;φ、λ表示载体的真实位置的经纬度;Γij表示真实位置处的地磁梯度;v(k)为量测噪声。
3.2 粒子滤波组合导航算法
地磁梯度观测值是载体真实位置的函数,其对应关系为典型的非线性关系,同时惯性导航系统定位存在积累误差,载体的真实位置(φ,λ)也无法直接获得。因此,常用线性近似方法将非线性函数Γij(φ,λ)在当前时刻滤波估值附近取一阶泰勒级数展开。然而由于基准梯度图采用离散格网的存储形式,梯度数据和位置难以用解析函数表示,式(14)所示的量测方程中的观测矩阵难以求导,因此只能通过平面拟合等方法确定观测矩阵的参数[20]。采用粒子滤波可避免上述方法线性化和观测矩阵的求解过程,粒子滤波通过随机采样的粒子及其权值近似系统状态的概率分布,并通过惯性导航系统指示位置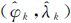 和粒子滤波器生成的位置误差后验概率分布(δφk,δλk)来代替载体的真实位置,则系统量测方程可转换为
和粒子滤波器生成的位置误差后验概率分布(δφk,δλk)来代替载体的真实位置,则系统量测方程可转换为
粒子滤波组合导航算法可从基准梯度图中直接计算出当前位置的梯度预测值Γij,当最新观测值yij(k)获得时,粒子滤波再通过重要性密度函数,利用预测梯度值和观测梯度值之间的差值,更新粒子权值,得到系统状态的估计。辅助导航系统中粒子滤波所采用的重要性密度函数为
式中,ωkn表示第n个独立同分布粒子在k时刻的重要性权值;R为测量噪声的方差阵。粒子滤波通过更新和递推,不断估计惯性导航系统的位置误差,校正系统位置输出,从而使系统位置的误差逐渐趋近于零。
地磁梯度辅助导航中观测量增加为6维后,系统状态后验概率密度尖峰变窄,虽然增强了匹配特征,有助于提高定位精度,但也使得大部分不在真实状态附近的粒子权值很小,加速重采样过程中粒子退化。基本粒子滤波方法缺乏生成新粒子的能力,当所剩粒子不能代表真实的后验概率密度时,将导致滤波算法失败。因此,通过引入人工物理优化(artificial physics optimized,APO)方法,本文将粒子抽象为质点力源,每个粒子在感知范围内可对周围其他粒子施加大小不等的引力和斥力,同时也具备感知其他粒子对自己产生引力和斥力的能力。这种虚拟力大小取决于物理力模型,为避免导航算法中粒子分布过分重叠或拥挤,选取如下模型
式中,Fij表示sj对si的虚拟力;d(si,sj)为si与sj之间的欧氏距离;Dth为引力和斥力的阈值;Ka和Kr为系数,分别调整引力和斥力强度。
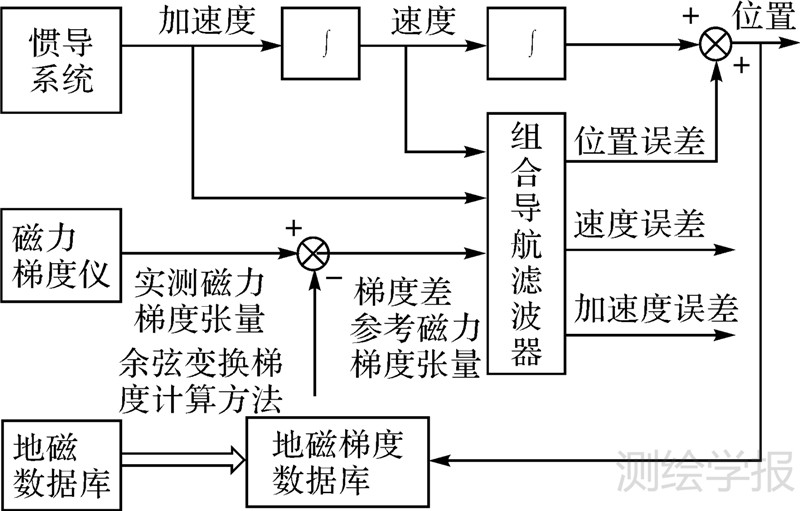
基于人工物理优化的改进粒子滤波算法,可改善粒子滤波中的粒子退化和样本贫化问题,引力和斥力使优化粒子之间保持紧密同时又避免过分集中,使粒子滤波在惯性/地磁梯度组合导航中具备了较强的收敛性和全局寻优能力,组合导航系统框图如图 1所示。
|
| 图 1 惯性/地磁梯度组合导航系统框图 Fig. 1 Schematic of INS/geomagnetic gradient integrated navigation system |
为验证惯性/地磁梯度组合导航系统的可行性,首先利用实测地磁异常垂向分量数据,通过本文推导得出的基于余弦变换导数计算方法,计算获得全张量地磁梯度导航基准图数据。然后将人工物理优化粒子滤波算法(APO-PF)应用于惯性/地磁梯度组合导航中,与常规粒子滤波方法(PF)比较,分析导航系统定位精度。
4.1 导航基准图梯度数据计算仿真结果本文从美国国家地球物理数据中心下载2002年发布的项目编号为CA_4232的美国加州地区某处航磁测量数据作为仿真试验数据,用于测试地磁梯度基准图构建以及地磁梯度辅助导航算法。对航磁测线数据经过Kriging插值、滤波处理形成分辨率为30″网格数据,数据经度范围:0°E-2°E,纬度范围:0°N-2°N,如图 2所示。表 1给出了地磁异常数据的特征统计。

|
| 图 2 地磁异常垂向分量及INS航迹 Fig. 2 Geomagnetic vertical component and INS recorded track |
| nT | ||||
| 特征统计 | 最大值 | 最小值 | 绝对均值 | 标准差 |
| 单位 | 351.12 | -354.98 | 122.54 | 147.35 |
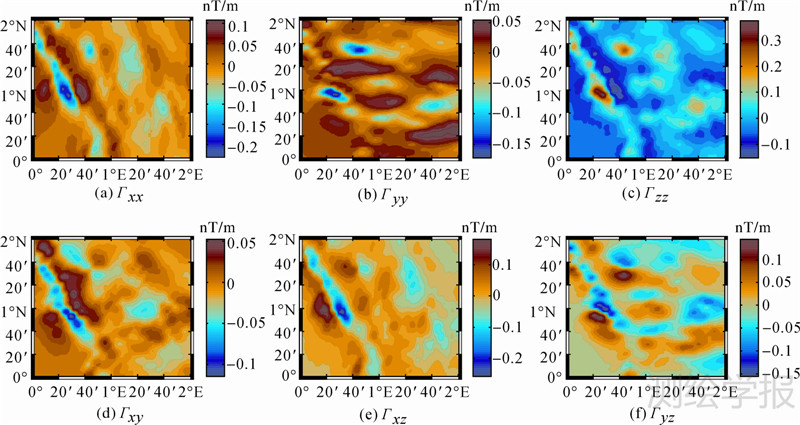
为实现高精度地磁梯度辅助导航,利用地磁异常数据构建全张量地磁梯度基准图数据库,首先利用表 1中所示磁异常垂向分量常数据计算其二维离散余弦变换Bz(u,v),然后通过上文中推导的全张量磁梯度频域正演公式(8)计算获得地磁梯度6个分量的频域结果,最后利用移相π/2离散余弦变换的逆变换获得地磁梯度分量的空间域结果。图 3(a)-图 3(a)(f)给出了实测地磁数据正演地磁梯度各分量的结果,其数据统计特征如表 2所示。
|
| 图 3 地磁梯度辅助导航基准梯度图 Fig. 3 The reference map of geomagnetic gradient aided navigation |
| nT/m | ||||
| 梯度分量 | 最大值 | 最小值 | 绝对均值 | 标准差 |
| Γxx | 0.126 6 | -0.230 9 | 0.028 1 | 0.037 9 |
| Γyy | 0.065 4 | -0.172 1 | 0.022 8 | 0.030 2 |
| Γzz | 0.403 0 | -0.151 2 | 0.043 4 | 0.057 2 |
| Γxy | 0.061 0 | -0.114 3 | 0.015 7 | 0.020 7 |
| Γxz | 0.204 4 | -0.256 1 | 0.033 1 | 0.044 0 |
| .Γyz | 0.160 8 | -0.154 9 | 0.029 0 | 0.037 2 |
仿真试验以GPS的位置信息作为载体真实位置的参照,分析惯导系统随时间积累的位置误差,并且对比分析采用常规粒子滤波和人工物理优化粒子滤波组合导航系统的定位精度。地磁梯度数据的实际观测值采用GPS指示的真实位置处的地磁梯度数据加入高斯白噪声来模拟。
载体利用惯性导航系统航行0.5 h后,将两种粒子滤波算法分别加入组合导航系统中。选取仿真条件:粒子滤波初始时载体位置误差和方差均为δφ0=δλ0=500 m;粒子数n=100;滤波周期t=10 s;仿真时间3 h;系统噪声w(k)选取常值陀螺漂移误差为εx=εy=εz=0.01°/h;加速度计零位误差为ΔAx=ΔAy=50 μg;量测噪声v(k)取σv2=0.002 nT/m。
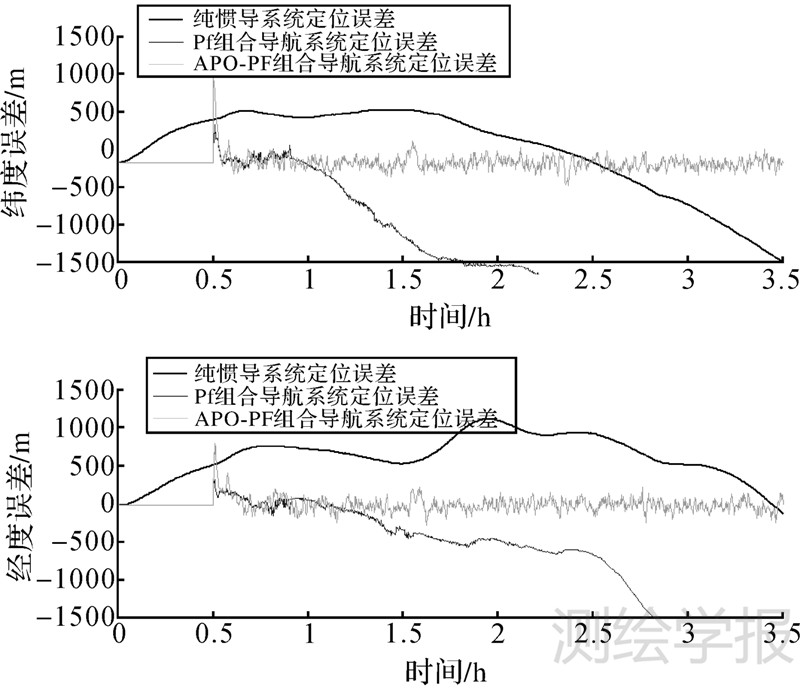
通过对基于粒子滤波的地磁梯度辅助定位方法进行仿真,图 4分别给出了纯惯导以及分别采用两种粒子滤波算法的组合导航系统定位误差仿真结果。分析可知,采用纯惯导时系统定位误差随时间累积而逐渐增大,在加入常规粒子滤波算法后,可有效地修正惯导系统的定位误差。然而随着滤波时间的增加,使得少数粒子的权值系数很大,而大多数粒子的权值都小得可以忽略,并且由于地磁梯度辅助导航中系统观测量维数较高,通过重采样过程也不能很好地解决粒子退化问题。从图 4中可知,在组合导航系统运行1 h后,常规粒子滤波算法滤波逐渐发散,定位误差增大。但是本文提出的APO-PF粒子滤波算法,通过调节粒子之间引力和斥力的变化,能够在较高的观测维数下维持滤波算法的稳定性,使得组合导航系统在长时间定位时保证较高的精度。
|
| 图 4 惯性/地磁梯度组合导航系统定位误差分析 Fig. 4 Analysis of the position error for INS/geomagnetic gradient integrated navigation system |
表 3给出了利用APO-PF算法组合导航系统独立仿真20次,载体经纬度位置估计的均方根误差(RMSE)结果,其中RMSE值计算公式如下
式中,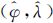 APO-PF,m和(φ,λ)GPS,m分别代表第m次仿真试验中APO-PF算法获得的经纬度位置估计,以及GPS指示的真实位置信息。
APO-PF,m和(φ,λ)GPS,m分别代表第m次仿真试验中APO-PF算法获得的经纬度位置估计,以及GPS指示的真实位置信息。
| nT/m | ||
| 定位误差(RMSE) | 经度 | 纬度 |
| 纯惯导系统 | 634.29 | 515.51 |
| APO-PF组合导航系统 | 60.89 | 66.41 |
通过使用地磁数据正演计算获得的地磁梯度数据进行匹配滤波,使APO-PF组合导航系统取得了60 m左右的定位结果,提高了导航系统定位精度,表明全张量地磁梯度在惯性/地磁组合导航系统中具有良好的应用价值。
5 结 论地磁场是地球固有的、可利用的无源信息,本文针对现阶段地磁梯度矢量测量尚未广泛展开,提出了基于移相π/2余弦变换时域微分定理的全张量地磁梯度计算方法,通过实测地磁异常数据进行验证,并将其作为导航基准图应用于惯性/地磁梯度组合导航系统中,利用人工物理优化改进的粒子滤波算法,提高了导航系统的定位精度,可较好地修正惯导系统随时间积累的误差。
| [1] | WESTON J L, TITTERTON D H. Modern Inertial Navigation Technology and Its Application[J]. Electronics and Communication Engineering Journal,2000, 12(2): 49-64. |
| [2] | KI LEE J, JEKELI C. Neural Network Aided Adaptive Filtering and Smoothing for an Integrated INS/GPS Unexploded Ordnance Geolocation System[J]. Journal of Navigation,2010, 63(2): 251-267. |
| [3] | LIU Li, ZHAN Xingqun, LIU Wei, et al. Assessment of Radio Frequency Compatibility between Compass and GPS[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(S1): 11-18. (刘莉,战兴群,刘卫,等. 北斗卫星导航系统和GPS兼容性评估(英文)[J]. 测绘学报, 2011,40(S1): 11-18.) |
| [4] | METZGER J, MEISTER O, TROMMER G F, et al. Adaptations of a Comparison Technique for Terrain Navigation[J]. Aerospace Science and Technology,2005, 9(6): 553-560. |
| [5] | KAN E M, LIM M H, ONG Y S, et al. Extreme Learning Machine Terrain-based Navigation for Unmanned Aerial Vehicles[J]. Neural Computing and Applications,2013, 22(3-4): 469-477. |
| [6] | LI Zhuang, LEI Zhihui, YU Qifeng. Matching Multi-sensor Images Based on Gradient Radius Angle Pyramid Histogram[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 318-325. (李壮,雷志辉,于起峰. 基于梯度径向夹角直方图的异源图像匹配[J]. 测绘学报,2011, 40(3): 318-325.) |
| [7] | HEMANT K, THBAULT E, MANDEA M, et al. Magnetic Anomaly Map of the World: Merging Satellite, Airborne, Marine and Ground-based Magnetic Data Sets[J]. Earth and Planetary Science Letters,2007, 260(1-2): 56-71. |
| [8] | GUAN Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing:Geological Publishing House, 2005. (管志宁. 地磁场与磁力勘探[M]. 北京:地质出版社, 2005.) |
| [9] | YANG W, HU C, LI M, et al. A New Tracking System for Three Magnetic Objectives[J]. IEEE Transactions on Magnetics, 2010, 46(12): 4023-4029. |
| [10] | SHI Guiguo, ZHOU Jun, GE Zhilei. Navigation Error of Inertial/Geomagnetic Navigation Technology for Cruise Aircraft[J]. Journal of Chinese Inertial Technology,2010, 18(1): 70-75. (施桂国,周军,葛致磊. 巡航飞行器惯性/地磁组合导航方法的误差[J]. 中国惯性技术学报,2010,18(1): 70-75.) |
| [11] | LIU Yuxia, ZHOU Jun, GE Zhilei. Geomagnetic Matching Algorithm Based on Hidden Markov Model[J]. Journal of Chinese Inertial Technology,2011, 19(2): 224-228. (刘玉霞,周军,葛致磊. 基于隐马尔可夫模型的地磁匹配算法[J]. 中国惯性技术学报,2011,19(2): 224-228.) |
| [12] | SCHMIDT P, CLARK D, LESLIE K, et al. GETMAG-a SQUID Magnetic Tensor Gradiometer for Mineral and Oil Exploration[J]. Exploration Geophysics,2004, 35(4): 297-305. |
| [13] | FOSS C. Improvements in Source Resolution that Can be Expected from Inversion of Magnetic Field Tensor Data[J]. Leading Edge (Tulsa, OK),2006, 25(1): 81-84. |
| [14] | STOLZ R, ZAKOSARENKO V, SCHULZ M, et al. Magnetic Full-tensor SQUID Gradiometer System for Geophysical Applications[J]. Leading Edge (Tulsa, OK),2006, 25(2): 178-180. |
| [15] | TILBROOK D L. Rotating Magnetic Tensor Gradiometry and a Superconducting Implementation[J]. Superconductor Science and Technology,2009, 22(7):101-106. |
| [16] | ZHANG Fengxu, MENG Lingshun, ZHANG Fengqin, et al. A New Method for Spectral Analysis of the Potential Field and Conversion of Derivative of Gravity-anomalies: Cosine Transform[J]. Chinese Journal of Geophysics,2006, 49(1): 244-248. (张凤旭,孟令顺,张凤琴,等. 重力位谱分析及重力异常导数换算新方法——余弦变换[J]. 地球物理学报,2006, 49(1): 244-248.) |
| [17] | LIU Fanming, ZHANG Yingfa, JIN Xin. Gravity Gradient Parkers Forward Method and Application Using Cosine Transform[J]. Acta Geodaetica et Cartographica Sinica,2013, 42(2): 177-183. (刘繁明,张迎发,荆心,等. 利用余弦变换的重力梯度Parker正演方法及其应用[J]. 测绘学报,2013, 42(2): 177-183.) |
| [18] | MICKUS K L, HINOJOSA J H. The Complete Gravity Gradient Tensor Derived from the Vertical Component of Gravity: A Fourier Transform Technique[J]. Journal of Applied Geophysics,2001, 46(3): 159-174. |
| [19] | WANG Wenjing. Underwater Navigation Methods Based on Gravity and Environmental Features[D]. Harbin: Harbin Engineering University, 2009. (王文晶. 基于重力和环境特征的水下导航定位方法研究[D]. 哈尔滨:哈尔滨工程大学, 2009.) |
| [20] | LIU Fengming. Research for Gravity Gradient Aided Inertial Navigation System[D]. Harbin: Harbin Engineering University, 2010. (刘凤鸣. 重力梯度辅助导航定位技术研究[D]. 哈尔滨:哈尔滨工程大学, 2010.) |
| [21] | LIU Fanming, QIAN Dong, LIU Chaohua. An Artificial Physics Optimized Particle Filter[J]. Control and Decision,2012, 27(8): 1145-1149. (刘繁明,钱东,刘超华. 一种人工物理优化的粒子滤波算法[J]. 控制与决策, 2012, 27(8): 1145-1149.) |