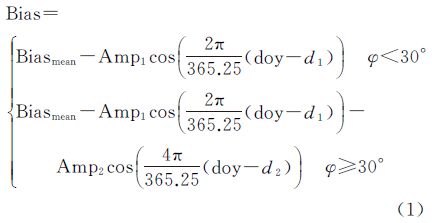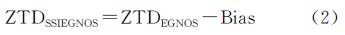2. 桂林理工大学 测绘地理信息学院,广西 桂林 541004;
3. 广西空间信息与测绘重点实验室,广西 桂林 541004;
4. 武汉大学 测绘学院,湖北 武汉 430079
2. College of Geomatic Engineering and Geoinformatics,Guilin University of Technology,Guilin 541004,China;
3. Guangxi Key Laboratory of Spatial Information and Geomatics,Guilin 541004,China;
4. School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China
1 引 言
对流层延迟是GNSS导航定位的重要误差源,在天顶方向延迟量大约为2 m,在接近地面方向时,其影响约为20 m[1],因此,在GNSS实际导航定位应用中,需要对对流层延迟进行改正。将对流层延迟作为待估参数一起参与平差能得到较精密的对流层改正信息[2, 3],但是难以满足对流层延迟改正的预报应用要求。而近年来,许多学者在建立区域的对流层改正模型时考虑了高程和水平方向的影响因子[4, 5, 6, 7, 8, 9],这些模型不需要气象参数,且具有较高的改正精度,但在其他大范围区域的应用有待验证。文献[10]利用中国地壳观测网GPS数据建立了中国地区VLBI站的单站实时对流层改正模型,其改正精度能满足VLBI用于精密测轨的对流层延迟改正要求,但是该模型需要实测的气象数据。
在当前的实时导航定位中,利用气象观测的数值预报资料成为了计算天顶对流层延迟(ZTD)的一种有效手段[11, 12]。文献[13, 14]评估了在中国地区及亚洲地区利用ECMWF/NECP资料计算ZTD的精度,其中ECMWF资料计算ZTD的偏差和RMS分别为-1.0 cm和2.7 cm,NECP资料计算ZTD的偏差和RMS分别为2.4 cm和6.8 cm。美国国家环境预报中心、欧洲中尺度天气预报中心、北美和欧盟已应用ECMWF/NECP资料建立了用于局域地区的对流层延迟改正模型(UNB3)[15, 16]。在北美地区,模型计算的对流层天顶延迟偏差优于20 cm,平均偏差为2 cm,而在全球范围内,UNB3的改正精度与使用实测气象元素的Saastamoinen模型和Hopfield模型基本相当,但在高海拔地区其改正精度优于Saastamoinen模型[17]。文献[18]建立了中国地区的对流层改正模型(SHAO模型),其偏差和RMS分别为2.0 cm和4.5 cm。文献[1]建立了全球的ZTD改正模型(IGGtrop模型),其在全球的偏差和RMS分别为-0.8 cm和4.0 cm,优于同等条件下的UNB 3和UNB 3 m模型(其模型偏差和RMS分别为2.0 cm、0.7 cm和5.4 cm、5.0 cm)。欧盟对UNB3模型进行简化得到EGNOS模型,EGNOS模型不需要实测气象数据,使用方便,其全球平均对流层改正效果较好,但是在某些地区的偏差仍旧较大,该模型已经应用于美国、欧洲等地区的增强导航系统中,其平均偏差和RMS分别为2.0 cm和5.4 cm[1],但是EGNOS模型在亚洲地区的适用情况和精度评估方面的研究较少,亟须开展相关研究。此外,针对中国地区VLBI站的单站实时对流层改正模型需要实测气象参数的情况[10]以及亚洲地区VLBI站与IGS站并址(或相隔较近)建立的情况,建立一种不需要气象参数的单站对流层改正模型用于VLBI站的实时对流层改正具有一定的实际意义和应用价值。本文以亚洲地区46个IGS站2008-2010年实测的高精度ZTD作为参考值,得到EGNOS模型计算ZTD的日均偏差,利用傅里叶变换对亚洲地区46个IGS站2008-2010年日均偏差分别进行频谱分析,建立了亚洲地区无需要气象参数的EGNOS模型的单站修正模型(SSIEGNOS,single-site improved EGNOS),并对其在亚洲地区计算ZTD的精度及模型适用情况进行了评估,此外,对SSIEGNOS模型预测亚洲地区ZTD的偏差和RMS进行了统计分析。这些研究结果可为亚洲地区建立对流层延迟改正模型和VLBI用于精密测轨的实时大气改正提供重要参考。
2 数据来源及SSIEGNOS模型建立本文研究利用亚洲地区46个IGS站2008-2011年的高精度ZTD时间序列,分辨率为5 min,其中IGS站ZTD的精度为4 mm[19, 20]。EGNOS模型计算ZTD的具体过程详见文献[10, 17]。本文研究的范围为10°N-63°N、30°E-160°E,IGS站的点位分布如图 1所示。

|
| 图 1 亚洲地区IGS站点位分布 Fig. 1 The distribution of the IGS sites over Asia area |
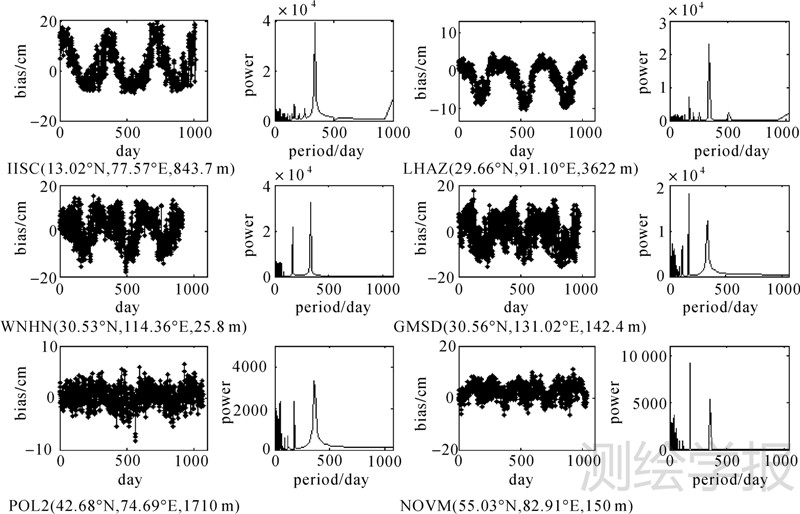
以分布于亚洲地区46个IGS站2008-2010年实测的高精度ZTD作为参考值,得到EGNOS模型计算ZTD的日均偏差。利用傅里叶变换对亚洲地区46个IGS站2008-2010年日均偏差分别进行频谱分析,发现纬度低于30°N的IGS站EGNOS模型计算ZTD的日均偏差变化都以年周期为主,而纬度高于30°N的日均偏差变化都以年周期和半年周期为主。图 2给出了其中6个IGS站日均偏差变化和相应的频谱分析结果。由图 2可以看出,日均偏差变化可以用余弦函数近似表示,因此,亚洲地区EGNOS模型计算ZTD的日均偏差可通过对各个站的3年日均偏差进行拟合求得,其表达式为
式中,年积日doy和日均Bias为已知量;φ为测站纬度;Biasmean为偏差的年均值;Amp1、Amp2分别为偏差的年周期和半年周期振幅;d1、d2分别为偏差的年周期和半年周期相位。利用各个测站3年的日均偏差值,采用非线性最小二乘法分别估计各站的上述参数,限于篇幅,各个测站系数的时空分布特征本文不作讨论分析。由此可得,SSIEGNOS模型计算ZTD的表达式为
式中,ZTDSSIEGNOS为SSIEGNOS模型计算的ZTD值;ZTDEGNOS为EGNOS模型计算的ZTD值;Bias是对EGNOS模型的修正值,由式(1)计算求得。
|
| 图 2 IISC、LHAZ、WUHN、GMSD、POL2及NOVM等6个IGS站2008-2010年日均偏差时间序列及相应的傅里叶频谱分析结果(站点后面括号内依次为测站纬度、经度和高程) Fig. 2 The variation of the daily bias and frequency spectral analysis based on Fourier transform at sites IISC,LHAZ,WUHN,GMSD,POL2 and NOVM in 2008-2010 |
以亚洲地区46个IGS站2008-2010年的ZTD时间序列作为参考值,对EGNOS和SSIEGNOS模型计算的ZTD进行精度评估,统计分析其偏差和RMS在时空上的分布特征。本文将EGNOS模型计算的日均ZTD减去IGS的日均ZTD得到日均偏差,根据RMS定义得到日均RMS,并由此计算得到相应的月均、季度和年均偏差和RMS。
3.1 偏差和RMS在时间上的分布特点 3.1.1 日平均偏差和RMS变化特征分析为了分析EGNOS和SSIEGNOS模型偏差和RMS每天的变化情况,现将各个IGS站的残差值按日进行统计分析。图 3给出了亚洲地区2008-2010年北部IRKJ站、西部CHUM站、东部TSK2站和南部CUSV站的偏差和RMS日均变化值,其他测站日均偏差和RMS的变化类似。

|
| 图 3 IRKJ、CHUM、TSK2和CUSV等IGS站EGNOS和SSIEGNOS模型的2008—2010年日均偏差和RMS Fig. 3 The variation of the daily bias and RMS in 2008—2010 at IRKJ, CHUM, TSK2 and CUSV sites for the EGNOS model and SSIEGNOS model respectively |
由图 3可以看出,EGNOS模型的日均偏差和RMS 均有明显的周期变化,日均偏差和RMS均在夏季达到最大值,容易发现西部CHUM站日均偏差和RMS相对亚洲其他地区变化较小。东部TSK2站受海洋气候的影响,且处于海洋和陆地交界处,水汽变化较剧烈,因此,夏季日均偏差和RMS变化幅度相对较大,而南部CUSV站处于亚洲低纬度地区,受海洋气候和热带气候的综合影响,夏季日均偏差和RMS变化较大。SSIEGNOS模型的日均偏差和RMS变化较小且平稳,无明显周期,即使在东部和南部的夏季也未出现大的波动,说明SSIEGNOS模型修正效果明显。
3.1.2月平均和季度偏差及RMS变化特征分析为了分析EGNOS和SSIEGNOS模型的偏差和RMS在季节上的变化特征,现将亚洲地区的46个IGS跟踪站2008-2010年的偏差和RMS分别进行月统计和季节统计,统计结果如图 4和表 1所示。

|
| 图 4 亚洲地区2008—2010年EGNOS和SSIEGNOS模型月平均偏差和RMS统计 Fig. 4 The variation of monthly bias and RMS for the EGNOS model and SSIEGNOS model in 2008—2010 over Asia area |
| cm | |||||
| EGNOS | SSIEGNOS | ||||
| 偏差 | RMS | 偏差 | RMS | ||
| 春季 | 2.269 | 5.021 | 0.049 | 2.418 | |
| 夏季 | -4.287 | 6.554 | 0.098 | 2.604 | |
| 秋季 | -0.049 | 5.562 | 0.012 | 3.060 | |
| 冬季 | 2.865 | 4.612 | 0.227 | 2.303 | |
图 4表明,亚洲地区EGNOS模型计算ZTD的偏差和RMS有明显的季节效应,偏差在夏季月份的值增加明显,在8月份达到最大负偏差,说明在夏季亚洲地区水汽变化较大,使EGNOS模型计算的ZTD低于实测ZTD;RMS也在夏季月份明显增加,在8月份达到最大值,偏差和RMS在其他季节月份变化相对较平缓。而SSIEGNOS模型的月均偏差和RMS均无明显季节变化,且月份之间变化较小,说明SSIEGNOS模型在夏季的修正效果显著。
由表 1可以看出,EGNOS模型的偏差在夏季达到最大值,在秋季最小,RMS也在夏季达到最大值,但是在冬季达到最小;而SSIEGNOS模型的偏差在冬季最大,秋季最小,RMS在秋季最大,冬季最小,但是各季节之间变化较平稳。
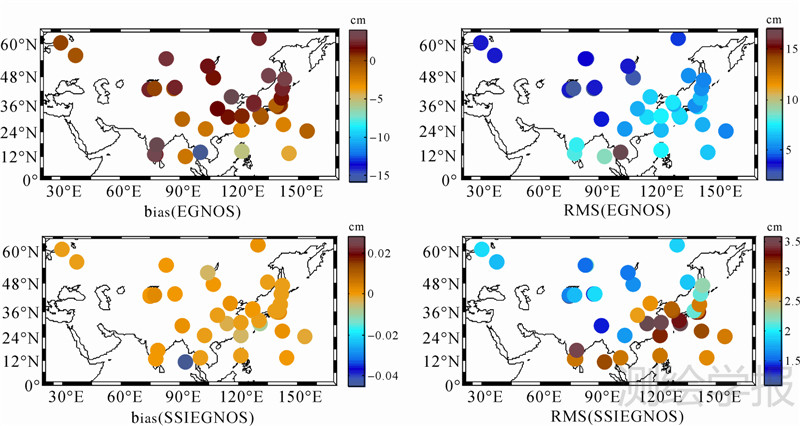
3.1.3 年均偏差和RMS变化特征分析对亚洲地区46个IGS站进行年均偏差和RMS统计,如图 5所示。由图 5可知,在亚洲西部和北部高纬度地区EGNOS模型年均偏差和RMS变化相对较小,东部和南部地区年均偏差和RMS变化较大;对于SSIEGNOS模型,其偏差和RMS在亚洲地区变化都比较小,尤其是在亚洲西部和北部高纬度地区其RMS优于2 cm,因此在亚洲西部和北部高纬度地区SSIEGNOS模型可用于高精度ZTD的研究和应用。相对于IGS站实测ZTD,亚洲地区SSIEGNOS模型计算ZTD的年均偏差和RMS明显优于EGNOS模型,SSIEGNOS模型的偏差和RMS分别为0和2.521 cm,EGNOS模型分别为0.12 cm和5.87 cm。相对于EGNOS模型,在低于纬度30°N的亚洲地区SSIEGNOS模型的偏差和RMS的绝对值分别减少了99%和62%,在高于纬度30°N的亚洲地区分别减少了99%和54%,在整个亚洲地区分别减少了99%和57%,说明SSIEGNOS模型在亚洲地区对EGNOS模型起到了明显的修正效果,尤其是在亚洲低纬度地区。另外还发现IGS站随着纬度的递增,两模型年均RMS在总体上均有减小的趋势,将在下一节进行详细分析。
|
| 图 5 EGNOS和SSIEGNOS模型年均偏差和RMS区域分布 Fig. 5 The distribution of yearly bias and RMS for EGNOS and SSIEGNOS models over Asian area in 2008—2010, respectively |
为了进一步分析中国地区EGNOS和SSIEGNOS模型计算ZTD的精度,本文将中国大陆8个IGS站进行年均偏差和RMS统计分析。结果表明,EGNOS模型在中国地区年均偏差和RMS分别为0.85 cm和5.37 cm,SSIEGNOS模型分别为0.003 cm和2.35 cm,说明SSIEGNOS模型在中国地区可以得到较高的ZTD改正精度。由此表明,在中国地区EGNOS模型足以满足GNSS实时导航定位对流层天顶延迟改正的需要,SSIEGNOS模型可应用于高精度ZTD的研究。
3.2年均偏差和RMS在空间上的分布特点 3.2.1 年均偏差和RMS在高程上的分布特点亚洲地区地势复杂、地形起伏较大,ZTD的分布与高程有密切的关系,因此ZTD的变化也比较复杂,为了分析EGNOS和SSIEGNOS模型年均偏差和RMS在高程上的变化特征,将46个IGS站的高程按照<500 m、500~1000 m、1000~1500 m、1500~2000 m、>2000 m范围划分,对每个高程范围的IGS站进行年均偏差和RMS统计分析,结果如图 6所示。图 6表明,随着高程的增加,EGNOS和SSIEGNOS模型年均偏差均无明显变化规律。但高程在1000~1500 m范围内时,EGNOS模型RMS突然变小,可能是由于在此高程范围内统计的IGS站数目较少,而随着高程的增加EGNOS和SSIEGNOS模型年均RMS总体上均有递减的趋势。
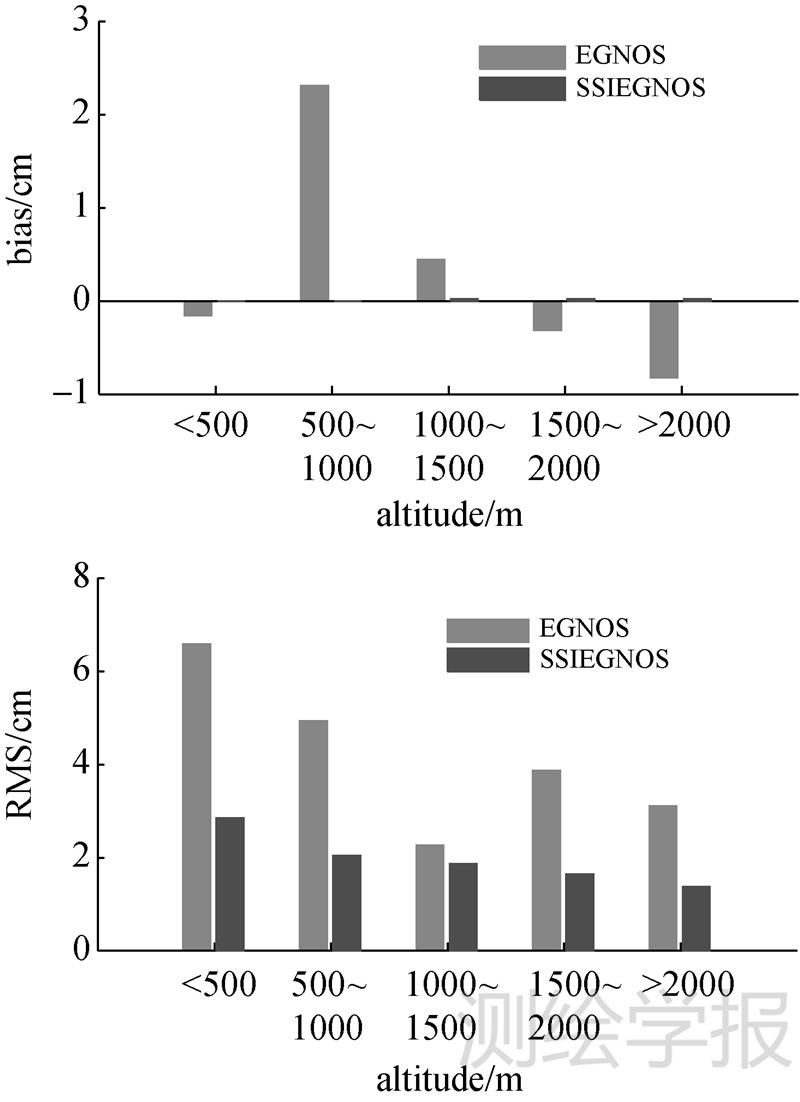
|
| 图 6 EGNOS和SSIEGNOS模型年均偏差和RMS在各个高程范围的变化关系 Fig. 6 The variation of the yearly bias and RMS in each altitude range for the EGNOS model and SSIEGNOS model |
亚洲地区地形地貌较复杂、气候多变,而且陆地和海洋分布广泛,因此ZTD的变化具有多样性。为了分析EGNOS和SSIEGNOS模型年均偏差和RMS在纬度上的分布特点,将46个IGS站按照纬度为10°N-20°N、20°N-30°N、30°N-40°N、40°N-50°N、>50°N的范围划分,对每个纬度范围的IGS站进行年均偏差和RMS统计,结果如图 7所示。由图 7可以明显地看出随着纬度的递增两种模型年均RMS均有减小的变化趋势。

|
| 图 7 EGNOS和SSIEGNOS模型年均偏差和RMS在各个纬度范围的变化关系 Fig. 7 The variation of the yearly bias and RMS in each latitude range for the EGNOS model and SSIEGNOS model |
为了分析EGNOS和SSIEGNOS模型的年均偏差和RMS在经度上的分布特点,将46个IGS站按照经度为<80°E 、80°E-90°E、90°E-100°E、100°E-110°E、110°E-120°E、120°E-130°E、130°E-140°E、>140°E的范围划分,对每个经度范围的IGS站进行年均偏差和RMS统计分析,结果如图 8所示。由图 8看出,两种模型的年均偏差和RMS在经度上都没有明显变化规律。
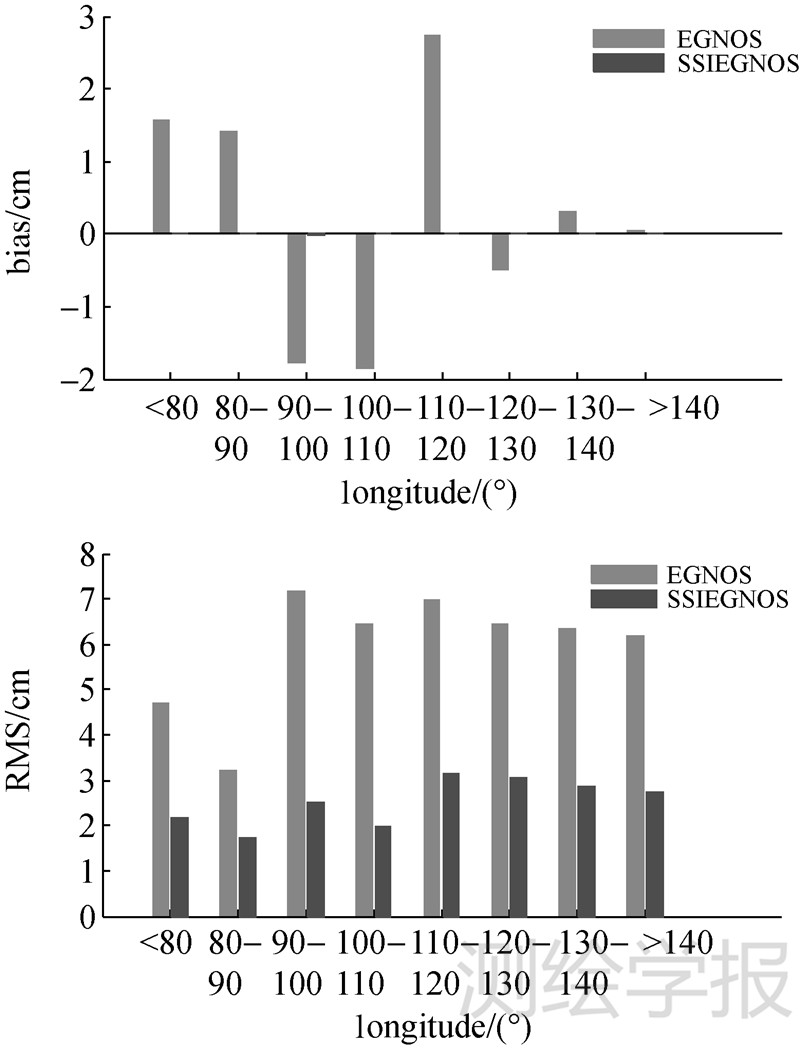
|
| 图 8 EGNOS和SSIEGNOS模型年均偏差和RMS在各个经度范围的变化关系 Fig. 8 The variation of the yearly bias and RMS in each longitude range for the EGNOS model and SSIEGNOS model |
为了进一步说明两种模型的年均偏差在经度上的变化关系,将两种模型的年均偏差与经度做相关性分析,结果如图 9(a)所示。图 9(a)说明两种模型年均偏差和经度的关系都比较小。

|
| 图 9 EGNOS和SSIEGNOS模型年均偏差与经纬度和高程的相关性分析 Fig. 9 Regression of yearly bias and longitude, latitude and altitude for the EGNOS model and SSIEGNOS model, respectively |
对两种模型的年均偏差与纬度做相关性分析,结果如图 9(b)所示。图 9(b)说明两种模型年均偏差与和纬度的变化无明显关系。
图 9(c)所示的年均偏差与高程的相关性分析说明EGNOS和SSIEGNOS模型年均偏差变化与高程的关系较小。
3.3 SSIEGNOS模型预测ZTD精度评估为了验证SSIEGNOS模型在亚洲地区预测ZTD的精度,以亚洲地区46个IGS站2011年高精度ZTD时间序列作为参考值,将上述建立的SSIEGNOS模型用于计算预测亚洲地区46个IGS站2011年的ZTD,并与EGNOS模型对比分析。统计亚洲地区46个IGS站2011年预测ZTD的年均偏差和RMS,得到SSIEGNOS模型和EGNOS模型的预测ZTD的年均偏差和RMS区域分布图,如图 10所示,相应的统计结果如表 2和图 11所示。
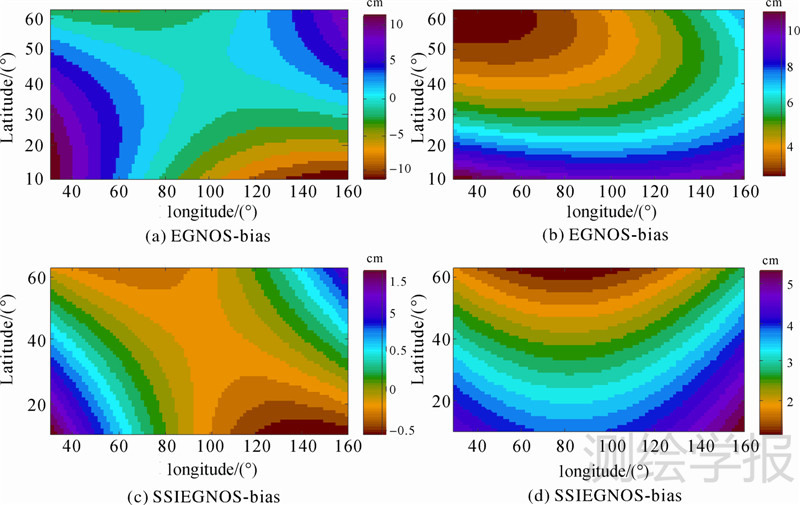
|
| 图 10 亚洲地区SSIEGNOS模型和EGNOS模型预测ZTD的年均偏差和RMS分布 Fig. 10 The distribution of the predicted ZTD of yearly bias and RMS for the EGNOS model and SSIEGNOS model over Asia area in 2011 |
| cm | ||
| EGNOS | SSIEGNOS | |
| 偏差 | -0.18[-17.5,3.99] | -0.08[-1.43,0.75] |
| RMS | 6.08[1.89,18.56] | 3.14[1.33,4.84] |
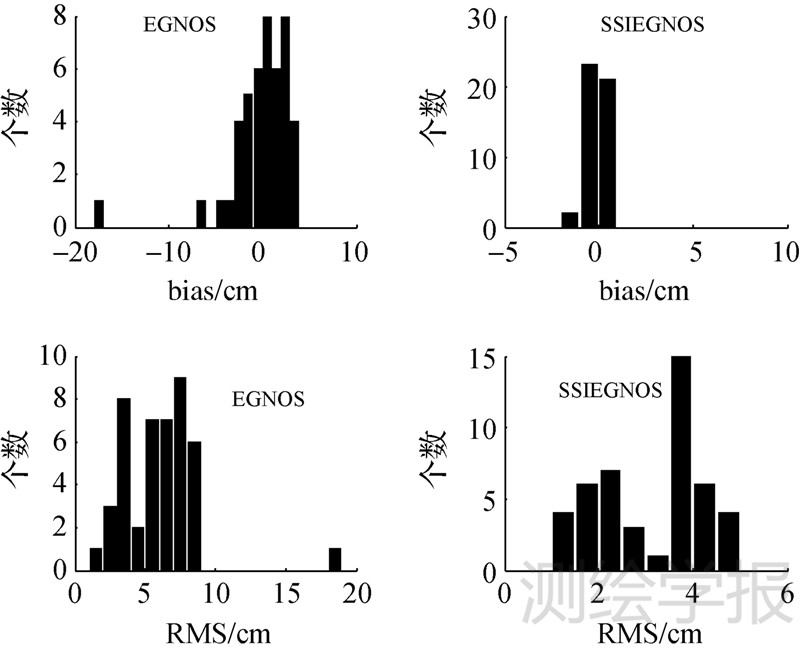
|
| 图 11 EGNOS和SSIEGNOS模型的亚洲地区预测偏差和RMS的分布直方图 Fig. 11 Distribution histogram of prediction bias and RMS for the EGNOS model and SSIEGNOS model over Asia area |
由表 2可知SSIEGNOS模型在亚洲地区预测ZTD的精度为厘米级,年平均偏差为-0.08 cm,RMS为3.14 cm,SSIEGNOS模型的平均偏差的绝对值小于EGNOS模型。图 10表明,EGNOS模型年均预测偏差在亚洲中部地区较小,在低纬度和东部地区较大,而SSIEGNOS模型预测偏差在整个亚洲地区都较小;EGNOS模型年均预测RMS在亚洲西北部高纬度地区约为4 cm,其他地区都较大,而SSIEGNOS模型在纬度高于30°N的地区其RMS优于3 cm,在亚洲东部和南部低纬度地区其RMS稍微偏大,但是在这些地区对ENGOS模型的修正效果最优,且其精度能保证在5 cm以内。相对于EGNOS模型,SSIEGNOS模型在低于纬度30°N的亚洲地区其预测偏差和RMS的绝对值分别减少了95%和54%,在高于纬度30°N的亚洲地区分别减少了94%和45%,在整个亚洲地区分别减少了55%和48%,但总体上SSIEGNOS模型在高于纬度30°N的亚洲地区预测ZTD的精度优于纬度30°N以下地区。此外,图 11给出了EGNOS和SSIEGNOS模型预测亚洲地区的年平均偏差和RMS分布直方图,图上显示SSIEGNOS模型的偏差都在-1.5~1.0 cm之间,RMS在1~5 cm之间,其偏差和RMS分布的集中程度明显高于EGNOS模型。表 2、图 10和图 11共同表明SSIENGOS模型在亚洲地区的预测ZTD精度明显优于EGNOS模型。
为了进一步分析SSIEGNOS模型预测偏差和RMS在季节上的变化特征,将亚洲地区46个 IGS站2011年的预测偏差和RMS进行月统计和季节统计,结果如图 12所示。由图 12可知,两种模型的月均偏差和季节偏差均无明显规律,EGNOS模型预测RMS有明显的季节变化,在夏季月份变化较大,且表现为夏季大,冬季小,而SSIEGNOS模型的RMS在各月份变化较小,其季节变化表现为秋季稍大,冬季小,因此,SSIEGNOS模型受季节变化影响相对较小。

|
| 图 12 亚洲地区SSIEGNOS模型和EGNOS模型预测偏差和RMS季节变化 Fig. 12 Seasonal variation of prediction bias and RMS for the EGNOS model and SSIEGNOS model over Asia area |
综上所述,将SSIEGNOS模型作为单站预报模型使用,其精度与文献[10]建立的中国地区VLBI站单站的实时对流层改正模型精度相当,由于SSIEGNOS模型不需要气象参数,因此该模型作为亚洲地区VLBI站的单站实时对流层改正模型使用具有一定的应用价值。
4 结 论相对于EGNOS模型,本文建立的SSIEGNOS模型在亚洲地区计算ZTD的精度有明显改善,尤其是在亚洲西部和北部的高纬度地区,其年均RMS优于2 cm,因此在这些区域可进行高精度ZTD的研究和应用。SSIEGNOS模型在夏季和亚洲低纬度地区对EGNOS模型的修正效果最佳。此外,利用SSIEGNOS模型进行亚洲地区ZTD预测,其年均RMS优于4 cm。由于SSIEGNOS模型无须任何气象参数且在亚洲地区具有较高的ZTD预测精度,因此建议将SSIEGNOS模型作为VLBI站精密测轨的实时ZTD改正模型使用。本文对亚洲地区EGNOS模型只进行了单站修正,而对整个亚洲区域EGNOS模型的修正有待进一步研究。
致谢:衷心感谢IGS中心提供天顶对流层延迟数据。
| [1] | LI Wei, YUAN Yunbin, OU Jikun, et al. A Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Sciences Bulletin, 2012, 57(15): 1317-1325. (李薇,袁运斌,欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报,2012, 57(15):1317-1325.) |
| [2] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Extracting Precise Atmosphere Propaganda Delays from Multiple Reference Station GPS Networks [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 523-528. (张宝成,欧吉坤,袁运斌, 等. 多参考站GPS网提取精密大气延迟[J]. 测绘学报,2012, 41(4): 523-528.) |
| [3] | YI Zhonghai, CHEN Yongqi, ZHU Jianjun, et al. An Approach to Regional Real Time Precise Point Positioning Based on IGS Ultra-rapid Orbit[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 226-231. (易重海,陈永奇,朱建军, 等. 一种基于IGS超快星历的区域性实时精密单点定位方法[J]. 测绘学报,2011, 40(2): 226-231.) |
| [4] | HUANG Dingfa, LI Chenggang, WU Yaoqiang, et al. Study of the Real-time Network Correction Genernation Approach for GPS/VRS Technique[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 256-261. (黄丁发,李成钢,吴耀强, 等. GPS/VRS实时网络改正数生成算法研究[J]. 测绘学报,2007, 36(3): 256-261.) |
| [5] | SHEN Xuefeng, GAO Chengfa, PAN Shuguo. Algorithm for Network RTK (VRS) Based on Star Structure[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 33-40. (沈雪峰,高成发,潘树国. 基于星型结构的虚拟参考站网络实时动态测量关键算法研究[J]. 测绘学报,2012, 41(1): 33-40.) |
| [6] | XIONG Yongliang, HUANG Dingfa, DING Xiaoli, et al. Research on the Modeling of Tropospheric Delay in Virtual Reference Station[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 118-132. (熊永良,黄丁发,丁晓利,等. 虚拟参考站技术中对流层误差建模方法研究[J]. 测绘学报,2006, 35(2): 118-132.) |
| [7] | LIU Lilong, HUANG Liangke, YAO Chaolong, et al. Research on 4D Modeling for Zenith Tropospheric Delays Based on Regional CORS Network[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 45-49. (刘立龙,黄良珂,姚朝龙, 等. 基于区域CORS网天顶对流层延迟4D建模研究[J]. 大地测量与地球动力学,2012, 32(3): 45-49.) |
| [8] | HUANG Liangke, LIU Lilong, YAO Chaolong. A Zenith Tropospheric Delay Correction Model Based on the Regional CORS Network[J]. Geodesy and Geodynamics, 2012, 3(4): 53-62. |
| [9] | DAI Wujiao, CHEN Zhaohua, KUANG Cuilin, et al. Modeling Regional Precise Tropospheric Delay[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 392-395. (戴吾蛟,陈招华,匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报: 信息科学版,2011, 36(4): 392-395.) |
| [10] | QU Weijing. The Research and Application of GPS Neutral Atmosphere Zenith Delay over China Area[D]. Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2007. (曲伟菁. 中国地区GPS中性大气天顶延迟研究及应用[D]. 上海:中国科学院上海天文台,2007.) |
| [11] | FARAH A, MOORE T, HILL C J. High Spatial Variation Tropospheric Model for GPS-data Simulation[J]. Journal of Navigation, 2005, 58(3):459-470. |
| [12] | BROMWICH D H, WANG S H. Evaluation of the NCEP-NCAR and ECMWF 15-and 40-yr Reanalyses Using Rawinsonde Data from Two Independent Arctic Field Experiments[J]. Monthly Weather Review: Special Section, 2005, 133(12): 3562-3578. |
| [13] | CHEN Q M, SONG S L, HEISE S, et al. Assessment of ZTD Derived from ECMWF/NCEP Data with GPS ZTD over China [J]. GPS Solution, 2011, 15(4): 415-425. |
| [14] | CHEN Qinming, SONG Shuli, ZHU Wenyao. An Analysis of the Accuracy of Zenith Tropospheric Delay Calculated from ECMWF/NCEP Data over Asian Area[J]. Chinese Journal of Geophysics, 2012, 55(5): 1541-1548. (陈钦明,宋淑丽,朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55(5): 1541-1548.) |
| [15] | IBRAHIM H E, EI-RRABBANY A. Regional Stochastic Models for NOAA-based Residual Tropospheric Delays[J]. Journal of Navigation, 2008, 61(2): 209-219. |
| [16] | PENNA N, DODSON A, CHEN W. Assessment of EGNOS Tropospheric Correction Model[J]. Journal of Navigation, 2001, 54(1): 37-55. |
| [17] | QU Weijing, ZHU Wenyao, SONG Shuli, et al. The Evaluation of Precision about Hopfield, Saastamoinen and EGNOS Tropospheric Delay Correction Model[J]. Acta Astronomica Sinica, 2008, 49(1): 113-121. (曲伟菁,朱文耀,宋淑丽, 等. 三种对流层延迟改正模型精度评估[J]. 天文学报, 2008, 49(1): 113-121.) |
| [18] | SONG Shuli, ZHU Wenyao, CHEN Qinming, et al. Establishment of a New Tropospheric Delay Correction Model over China Area[J]. Science China: Physics, Mechanics & Astronomy, 2011, 54(12): 2271-2283. |
| [19] | WANG Qianxin, XU Guochang, CHEN Zhengyang. Interpolation Method of Tropospheric Delay of High Altitude Rover Based on Regional GPS Network [J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1405-1407. (王潜心,许国昌,陈正阳. 利用区域GPS网进行高海拔流动站的对流层延迟量内插[J]. 武汉大学学报: 信息科学版,2010, 35(12): 1405-1407.) |
| [20] | DEBLONDE G, MACPHERSON S, MIREAULT Y, et al. Evaluation of GPS Precipitable Water over Canada and the IGS Network[J]. Journal of Applied Meteorology and Climatology, 2005, 44(1): 153-166. |