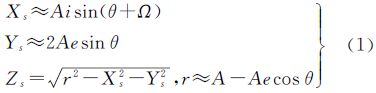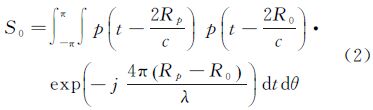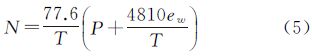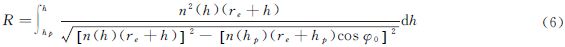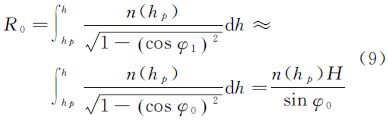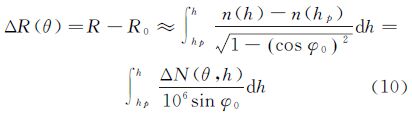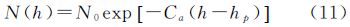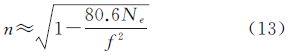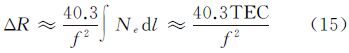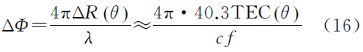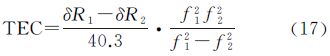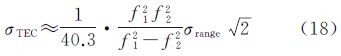2. 中国科学院 电子学研究所，北京 100190
2. Institute of Electronics,Chinese Academy of Sciences,Beijing 100190,China
1 引 言
圆迹SAR(circular SAR，CSAR)通过传感器平台的曲线运动，获取被观测目标多方位乃至360°全向观测信息，从而具有高精度的三维分辨能力[1, 2]。地球同步轨道SAR(geosynchronous SAR，GEOSAR)轨道高度高，利用很小的波束角即可实现大面积区域成像，且地球同步轨道SAR重访周期短，从而克服了低轨星载SAR重访周期长、覆盖面积小的缺点[3, 4, 5, 6]。通过设计一定的轨道参数，如偏心率、倾角，可使同步轨道卫星轨迹为近似圆形，从而使得地球同步轨道圆迹SAR(geosynchronous circular SAR，GEOCSAR)成为可能[7, 8, 9, 10]。结合了GEOSAR和CSAR的优点，GEOCSAR具有覆盖区域大、重访周期短、可获得高分辨率三维信息、对目标区域实现连续监测的优势，使得GEOCSAR拥有很强的发展前景[3, 8, 9]。
GEOCSAR运行于大约36 000km的高度之上，信号在传播过程中将不可避免地受到大气层的影响。本文考虑L波段GEOCSAR特点，因此对流层和电离层的影响均不可忽略。对流层和电离层具有明显的空时变化特性，大气折射率的时空不一致性将严重影响雷达无线电波传播，因而大气效应对SAR成像的影响一直以来是SAR技术研究的一个重要方面[11, 12, 13, 14, 15]。对流层在大气层的最底层，紧靠地球表面，对流层的影响主要考虑对流层折射率垂直变化造成的信号延迟[13, 14]。电离层对于较低频率的电磁波的折射、色散、衰减等效应会导致信号的传播延迟、相位失真、幅度衰落[15, 16, 17, 18]。文献[16]分析了电离层大气延迟影响以及大气延迟测量方法。文献[17]重点分析了电离层垂直变化导致的图像偏移、电离层色散导致的脉冲信号展宽等影响。文献[18]进一步研究了电离层不规则体对SAR方位向分辨率的影响，以及电离层水平变化引起的图像位移。
对于常规SAR成像，其合成孔径时间很短，因此一般无须考虑大气层时间变化对SAR成像的影响。而GEOCSAR合成孔径时间很长，一般在小时量级，实现全孔径成像时的合成孔径时间为24h，而对流层和电离层折射率变化都有明显的周日变化特性[19, 20, 21, 22]，因而大气折射率时间变化将对GEOCSAR方位向聚焦产生重要影响。本文重点分析和推导了对流层和电离层时间变化对GEOCSAR聚焦性能的影响，指出大气层时间变化是影响GEOCSAR成像的决定性因素之一，并给出相应的大气折射率时间变化影响补偿方案。
2 GEOCSAR成像几何影响同步轨道卫星轨迹的主要因素有：由卫星轨道倾角引起的纬度上的简谐振动；由卫星轨道偏心率引起的经度上的简谐振动。通过控制轨道倾角(i)、离心率(e)、近地点幅角(Ω)等轨道参数，可控制卫星航迹为直线、圆、椭圆等航迹。假定坐标系为以地球为中心的地固坐标系统，X轴指向北极，Z轴指向不发生偏移时卫星相对地球静止的位置，Y轴与XZ平面垂直，则卫星的坐标可表示为[7, 8]
式中，A是地球同步轨道半长轴；r表示卫星到地球中心的距离；θ∈[－π,π)表示慢时间域，对应同步轨道卫星运行一周(周期为1d)的时间间隔。假定i=2e(i用弧度表示)，Ω=π/2，则卫星运行航迹投影到XY面的轨迹为圆形，且圆周半径为Rg=Ai。
一般可用点目标响应函数来刻画SAR性能。与常规SAR类似，GEOCSAR全孔径成像时的点目标响应函数可表示为
式中，p(t)表示发射信号；Rp表示目标区域内任意点与SAR接收机的距离；R0表示点目标与SAR接收机的距离；λ表示波长；c表示光速。
若发射信号为线性调频信号，则理想的GEOCSAR点目标聚焦函数为[23]
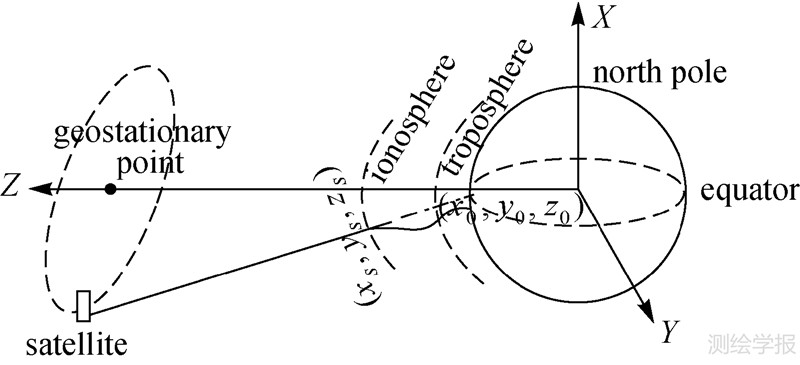
式中，C0表示常数；B表示带宽；dz表示高度向分辨单元；dp表示方位向二维分辨单元；J0(x)是零阶贝塞尔函数。由式(3)可知，理想方位向聚焦函数为零阶贝塞尔函数形式。
当电磁波穿过对流层和电离层时，折射率的变化使得目标与雷达之间的距离发生弯曲而偏离理想的直线距离。图 1是考虑大气效应时的地球同步轨道圆迹SAR成像几何图。
|
| 图 1 考虑大气效应时的地球同步轨道圆迹SAR成像几何图 Fig. 1 Imaging geometry of GEOCSAR with atmospheric effects |
对流层对雷达电波传播的影响程度可用介质磁导率μ和介电常数ε来表征，并以折射指数n=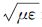
表示。大气折射指数n接近于1，为了研究和使用方便，引入了折射率N
大气折射率N的变化一般可用气象参数P、T和ew来表征。由电波传播理论和分子物理学，可得折射率为[21]
式中，P为所有气体的总压力(hPa)；ew为水汽压(hPa)；T为大气绝对温度。随着大气压、温度、湿度的变化，折射率不仅在空间上变化，在时间上也有明显的变化。
假定目标高度是hp，n(hp) 是高度hp位置的折射指数，n(h)表示h处的折射指数，则由射线跟踪法可得到电磁波穿过大气层时目标与雷达之间的实际距离[21]
式中，φ0是掠射角，由雷达位置与目标位置决定，可通过反演已知的目标水平距离和折射指数n及掠射角φ0的关系得到[12]。
理想距离R0是假定折射率为常数时得到
式中，φ1是理想直线距离时的掠射角，掠射角φ0和φ1非常接近。
由于对流层高度远小于地球半径，实际距离式(6)以及理想距离式(7)可简化为
式中，H表示对流层内雷达与目标之间的高度。由于大气折射指数n(h)、n(hp)相差不大，两者之差一般在10-6～10-4量级之间变化，则由对流层效应引起的斜距误差近似为 式中，ΔN(θ,h)表示N随θ和h的变化值。假设折射率N随高度呈指数形式变化，即 式中，N0为地面折射率；h为海拔高度(km)；hp为目标海拔高度；Ca为指数衰减系数(km-1)。GEOCSAR轨道高度非常高，对于地球上任意一块目标区域，掠射角φ0都将在80°以上，另外，我国Ca年平均值为0.140 4/km[19]，取对流层高度为12km，则由对流层时间变化引起的相位误差近似为
当相位误差ΔΦ大于π/4时，方位向聚焦性能会发生退化。因此，对于L波段GEOCSAR，当折射率N的周日变化均方差大于大约2.7N单位时，GEOCSAR方位向聚焦性能即会受到影响。
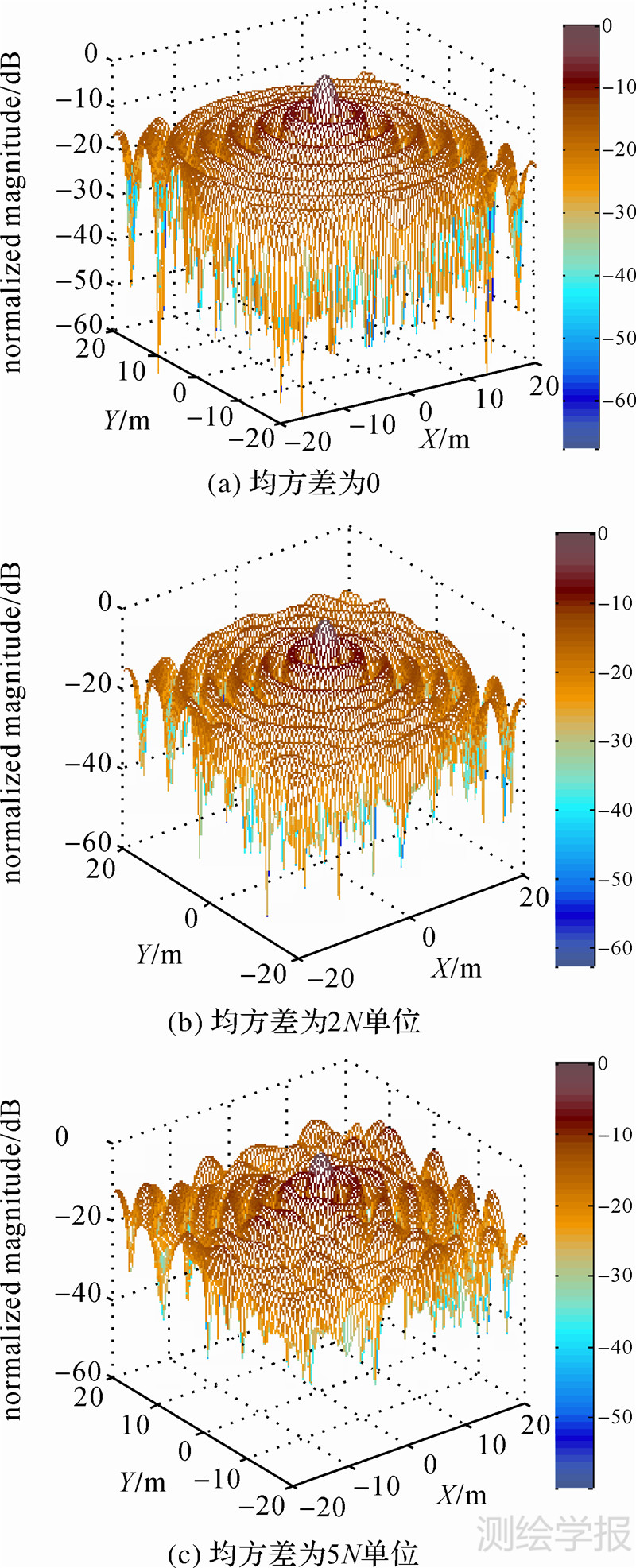
图 2(见文末)是加入均值为0，均方差分别为0N、2N和5N单位的正态分布的折射率随机日变化后的GEOCSAR点目标聚焦成像结果(本文的点目标成像仿真均利用共焦成像算法实现)。仿真中轨道倾角设置为0.78°，离心率为0.0068，波长为0.25m，由式(3)可计算得到方位向分辨率近似为5m×5m。图 2(a)即是理想点目标的XY平面二维点目标扩展函数(PSF)，其积分旁瓣比(ISLR)和峰值旁瓣比(PSLR)分别为-4.79dB和-7.9dB。由图 2可看出，2N单位的折射率日变化对成像性能影响很小，ISLR和PSLR分别为-4.6dB、-7.8dB；均方差5N单位的折射率日变化使成像性能发生了退化，X方向和Y方向ISLR和PSLR均分别下降了1.4dB和2.2dB左右。
|
| 图 2 加入均值为0的高斯分布的对流层折射率随机变化后的点目标2D PSF图 Fig. 2 2D PSF in the presence of tropospheric refractivity variation with zero mean Gaussian noise |
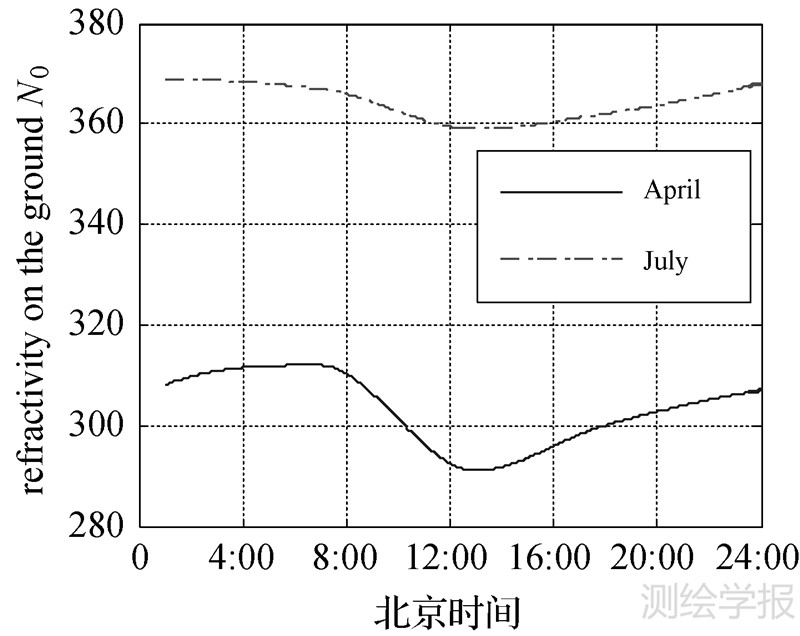
根据大气探空资料，如美国国家环境预报中心(National Centers for Environmental Prediction，NCEP)资料，可得一天内每个时间采样点的气象参数，代入式(5)可得N的日变化。图 3是北京地区在2002年4月和7月中间一天的对流层折射率日变化曲线。
|
| 图 3 对流层折射率日变化曲线 Fig. 3 Average value of tropospheric refractivity on the time of day |
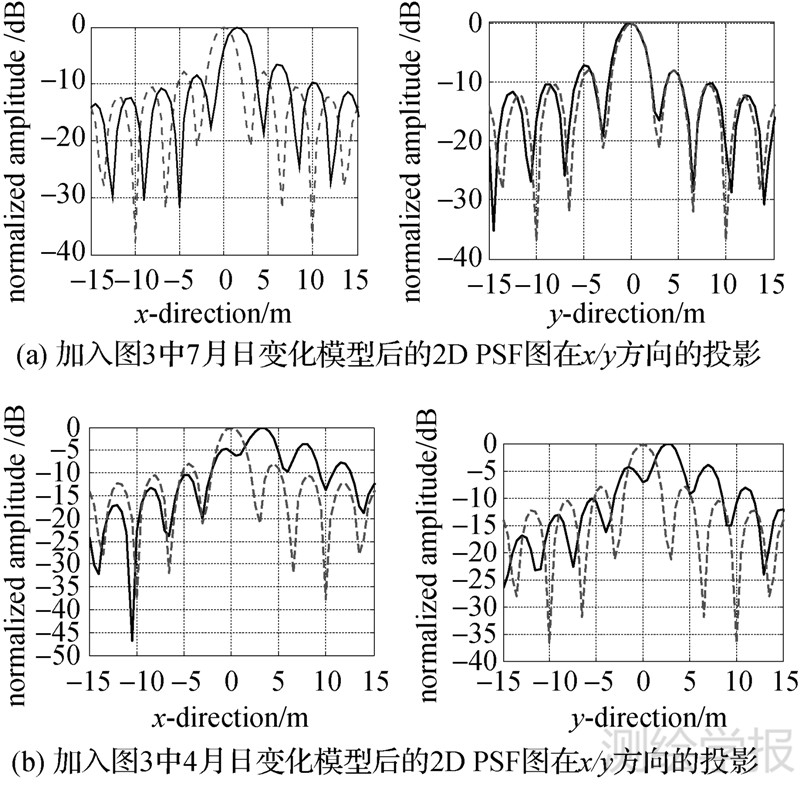
图 4是根据图 3的折射率日变化模型得到的GEOCSAR方位向PSF图，其中虚线表示理想聚焦结果，实线表示考虑对流层时间变化的点目标聚焦结果。由于图 3中的折射率N周日变化具有明显的周期性，因此会形成一次项斜距误差，从而使得重建点目标发生位移，7月折射率变化模型使得目标在y方向偏移1.5m，4月折射率变化模型使得目标在x、y方向分别偏移2m、2.5m。图 3中7月的折射率日变化均方差近似为2.5N单位，方位向聚焦性能影响较小；4月的折射率日变化均方差为7N单位，GEOCSAR方位向聚焦性能受到较大影响，图 4(b)中x、y向信号的ISLR和PSLR分别下降为-2.79dB和-4.5dB。
|
| 图 4 加入图 3中对流层折射率日变化模型后的2D PSF图在x/y方向的投影 Fig. 4 2D PSF projected on x/y-direction with the temporal variation model in Fig. 3 |
从图 2和图 4可看出，对流层折射率时间变化会影响GEOCSAR方位向聚焦，当折射率的日变化均方差大于3N单位左右时，对流层折射率的日变化会降低方位向ISLR和PSLR，这与理论分析吻合。因此，欲实现GEOCSAR聚焦成像，须对对流层折射率的日变化影响进行补偿。对对流层时间去相干影响的补偿可考虑采用基于外部测量数据如高精度数值气象模型的对流层湿延迟测量的方法(高精度对流层湿延迟测量精度可达2 mm左右，相应的相位误差为0.1 rad，因此具有较好的补偿精度)[24]。
4 电离层时间去相干对GEOCSAR聚焦性能影响描述电离层的主要参数是电离层的自由电子密度，单位是个电子/m3。由于大气层气体成分、温度等随高度的变化以及其他影响大气电离的因素的影响，电离层电子密度随高度呈现有规律的变化。在电离层中忽略电子碰撞和地磁场的影响，折射指数可近似表示为
式中，Ne为电离层电子密度；f表示信号频率。对于L波段SAR信号，上式可进一步化简为 则电离层折射率变化造成的斜距误差近似为 式中，R=∫dl为信号传播路径长度，TEC为积分电子含量(total electron content)，简称电子含量，定义为TEC=∫Nedl，单位为个电子/m3。
TEC具有明显的时空变化特性，而TEC随慢时间θ的变化所引起的方位向相位误差为
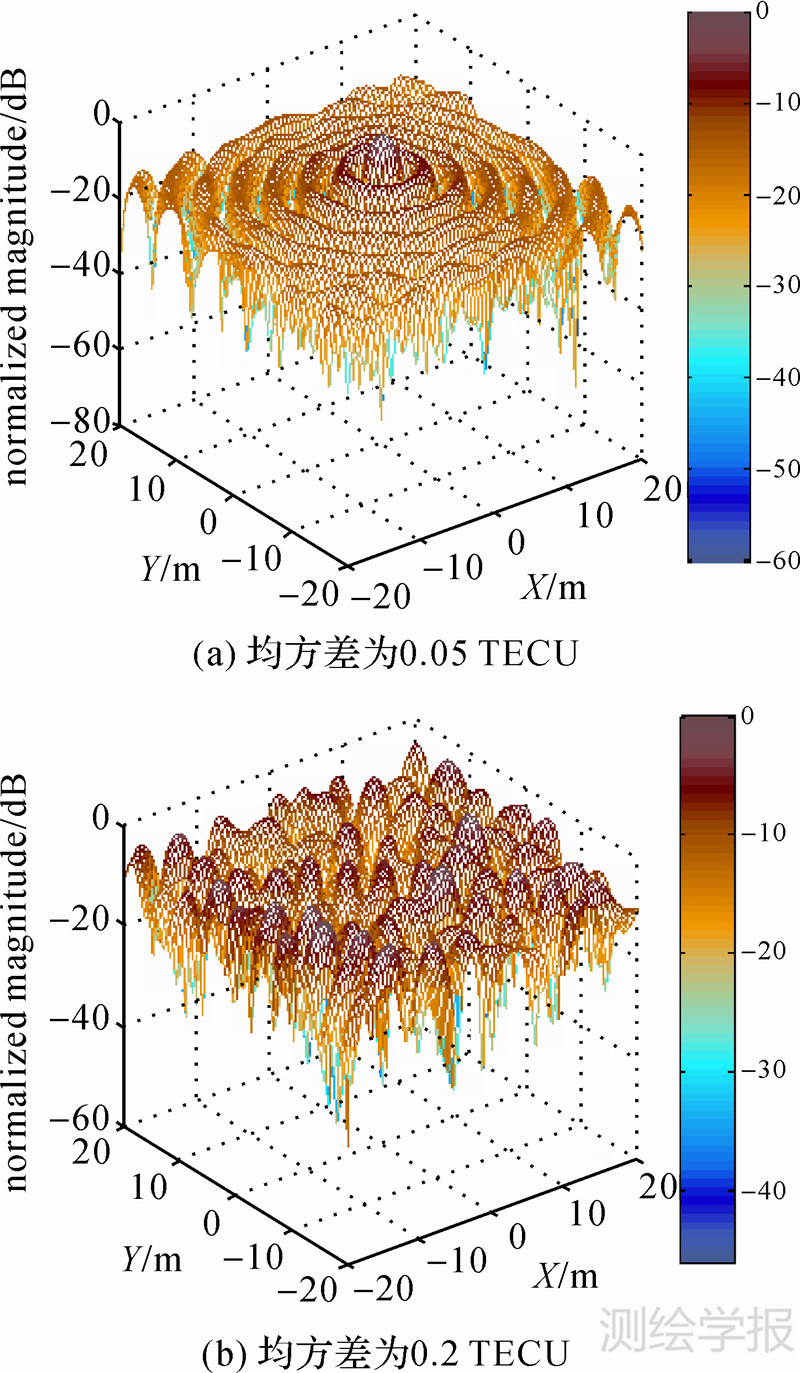
因此，对于L波段GEOCSAR，当电离层TEC的随机变化大于0.06TECU(1TECU=1016个电子/m3)左右时，方位向聚焦性能即会受到影响。图 5(见文末)是加入均值为0的正态随机分布TEC周日变化时的XY平面PSF图，其中图 5(a)中的随机噪声均方差为0.05TECU，图 5(b)的随机噪声均方差为0.2TECU。由图 5可看出，TEC在一个周期内的随机变化为0.05TECU时，电离层时间变化对GEOCSAR方位向聚焦性能的影响不大，而当TEC的随机变化在0.2TECU时，GEOCSAR方位向信号几乎完全散焦。
|
| 图 5 加入零均值正态分布的电离层TEC随机日变化后的2D PSF图 Fig. 5 2D PSF in the presence of ionospheric TEC variation with zero mean Gaussian noise |
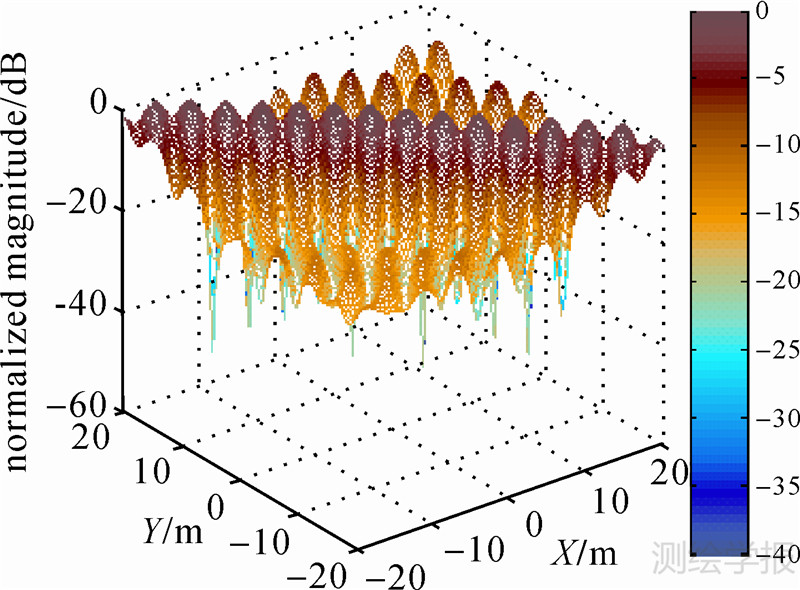
利用GPS资料，也可分析TEC周日变化统计分布情况。图 6是根据GPS间隔2h的测量数据，再经过最小二乘拟合得到的TEC在2001年第200天中国区域的TEC平均周日变化图。从图中可看出TEC的日变化近似为22TECU(随机变化均方差为7TECU)。基于图 6中的TEC周日变化模型，可得GEOCSAR的XY面PSF如图 7所示(见文末)。从图 7可看出SAR信号完全散焦。
|
| 图 6 2001年第100天中国区域的平均TEC周日变化图 Fig. 6 Average daily variation of TEC on the 100th day in 2001 for China |
|
| 图 7 对应图 6TEC变化模型的GEOCSAR点目标2D PSF图 Fig. 7 2D PSF with variation model of TEC in Fig. 6 for GEOCSAR |
大量的TEC历史数据的统计分析表明，白天TEC 12h的变化量大约为25TECU，晚上一般大约在8～15TECU之间，而随机TEC变化量也常可达到10TECU左右[14]。由上述分析可知，如此大的TEC随机周日时间变化量可导致GEOCSAR完全时间去相干，从而使得方位向信号完全散焦。
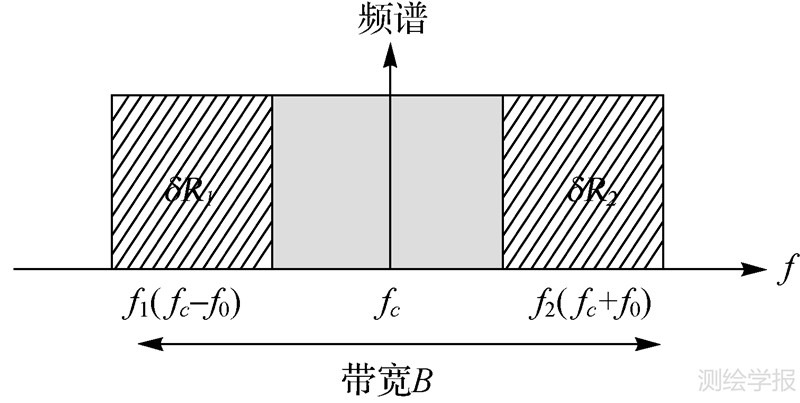
由于常规星载SAR合成孔径时间很短(常为秒量级)，电离层时间变化对SAR聚焦性能没有影响。而GEOCSAR合成孔径非常长(常为小时量级)，电离层时间去相干对GEOCSAR成像影响非常严重，欲完成GEOCSAR方位向聚焦成像，必须对电离层影响进行补偿。由式(15)可知，若已知TEC时空变化值，则可将TEC值代入信号模型中进行补偿。由于电离层是色散介质，所以可采用分谱的方法来估算TEC值(分谱法与GPS双频测量法类似，但由于GPS空间和时间采样密度不够，TEC测量精度不高)[25]。分谱法即是将信号的距离谱分成两个不重叠的子带，如图 8所示，从两个子带中得到不同载频对应的距离向偏移量。利用分谱法可对TEC值进行实时测量。
|
| 图 8 分谱法中子带与全带宽的关系 Fig. 8 Relation between the sub-band and full band for split spectrum approach |
由式(15)可知，电离层电子密度垂直变化会导致图像距离向发生偏移，且偏移量近似为40.3TEC/fc 2。若载频f1、f2(f1＜f2)两个子带所对应的距离向偏移分别为δR1、δR2，则可通过解两个方程估算得到TEC为
则分谱法测量TEC的均方误差σTEC近似为
式中，σrange为距离向偏移测量误差。假定距离向偏移测量的精度为1m(σrange=1m)，两个子带分别为20MHz(信号距离向带宽为50MHz，载频为1.2GHz)，则对于单个分辨单元的TEC测量精度为大约1TECU，这对电离层时间去相干效应的补偿还不够。为提高TEC测量精度，可考虑加大信号带宽或提高距离向偏移测量精度，或进行多视平滑处理。当带宽达到100MHz左右，对200个分辨单元取平均时，TEC测量精度可达到0.05TECU左右，但这又降低了SAR方位向分辨率。对于GEOCSAR成像，其方位向分辨率一般可达米量级(图 3)仿真中，倾角0.78°的L波段GEOCSAR的方位向分辨率为5m×5m)，当对200个单元作平均时，GEOCSAR方位向分辨率将下降到数百米或千米量级。因此，为保证一定的TEC测量精度和GEOCSAR高分辨率，可考虑结合分谱法和自聚焦算法。在分谱法准确测量TEC进行电离层效应校正后，可利用自聚焦算法对电离层时间变化的随机TEC残余误差进行补偿。 5 结 论
由于常规星载SAR合成孔径时间很短，可以不用考虑大气折射率时间变化对SAR聚焦性能的影响。而GEOCSAR合成孔径时间很长(全孔径成像时间为近似24h)，对于L波段GEOCSAR，对流层和电离层折射率时间变化均会影响SAR方位向信号聚焦。大气折射率的周日周期变化部分会导致目标重建位置在x、y向发生偏移，周日随机变化部分会导致SAR方位向聚焦性能退化甚至散焦。当对流层折射率周日随机变化均方差大于3N单位左右时，GEOCSAR方位向成像性能如ISLR、PSLR会发生退化，当折射率周日随机变化为5N单位时，ISLR和PSLR分别下降了1.4dB和2.2dB左右；当电离层TEC周日随机变化均方差大于0.06TECU左右时，GEOCSAR方位向聚焦即会受到影响，随着随机变化量的增大，如达到0.2TECU时，SAR方位向信号几乎完全散焦。所以，欲实现GEOCSAR正常聚焦成像，必须对大气效应时间去相干进行补偿。
实际中，对流层周日随机变化量一般在5N单位左右，而电离层周日变化量常可达到十几TECU，通常情况下电离层时间去相干会使GEOCSAR方位向信号完全散焦，因此电离层效应补偿对GEOCSAR成像至关重要。对于对流层效应，可利用基于高精度数值气象模型的对流层湿延迟测量方法进行补偿；对于电离层影响，可通过分谱法准确测量TEC数值代入信号模型来进行补偿，然后结合自聚焦方法补偿残余TEC随机变化。
| [1] | AKIA ISHIMARU, CHAN TSZ-KING, YASUO KUGA. An Imaging Technique Using Confocal Circular Synthetic Aperture Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1524-1530. |
| [2] | KOU Leilei, WANG Xiaoqing, CHONG Jinsong, et al. Circular SAR Processing Using an Improved Omega-k Type Algorithm[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 572-579. |
| [3] | Global Earthquake Satellite System. A 20 Year Plan to Enable Earthquake Prediction[EB/OL].[2003-01-23]. http://solidearth. jpl.nasa.gov/gess.html. |
| [4] | DAVIDE B, STEPHEN E H, GIUSEPPE O. Geosynchronous Synthetic Aperture Radar: Concept Design, Properties and Possible Applications[J]. Acta Astronautica, 2006, 59(5): 149-156. |
| [5] | MADSEN S N, WENDY E, LEO D. A Geosynchronous Synthetic Aperture Radar: for Tectonic Mapping, Disaster Management and Measurements of Vegetation and Soil Moisture[C]//Proceedings of IGARSS Proceedings. Hawaii: IEEE, 2001: 447-449. |
| [6] | HU Cheng, LONG Teng, ZENG Tao. The Accurate Focusing and Resolution Analysis Method in Geosynchronous SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3548-3563. |
| [7] | KIYO T. Synthetic Aperture Radar Imaging from an Inclined Geosynchronous Orbit[J]. IEEE Transactions on Geoscience and Remote Sensing, 1983, GE-21(3):324-329. |
| [8] | KOU Leilei, WANG Xiaoqing, XIANG Maosheng, et al. Interferometric Estimation of Three-dimensional Surface Deformation Using Geosynchronous Circular SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48 (2): 1619-1635. |
| [9] | LIU Qi, HONG Wen, TAN Weixian, et al. An Improved Polar Format Algorithm with Performance Analysis for Geosynchronous Circular SAR 2D Imaging[J].Progress in Electromagnetics Research,2011, 119:155-170. |
| [10] | LISA C, CARLO C, DAVIDE L, et al. A Ground-based Parasitic SAR Experiment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2132-2141. |
| [11] | QUEGAN S, LAMONI J. Ionospheric and Tropospheric Effects on Synthetic Aperture Radar Performance[J]. International Journal of Remote Sensing, 1986, 7(4):525-539. |
| [12] | SUN Jinping, BI Yuekai, WANG Yanping, et al. High Resolution SAR Performance Limitation by the Change of Tropospheric Refractivity[C]// Proceedings of IGARSS. Vancouver: IEEE, 2011:1448-1451. |
| [13] | LU Xiaoping. Series Expression of Correction for Curved Electronmagnetic Signal Path in Troposphere[J].Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 142-146. (卢小平.电磁波信号在对流层中路径弯曲改正的级数展开[J].测绘学报,2008, 37(2):142-146.) |
| [14] | DANKLMAYER A, BORING B J, SCHWERDT M. Assessment of Atmospheric Propagation Effects in SAR Images[J]. IEEE Transactions on Geoscience and Remote sensing, 2009, 47(10):3507-3518. |
| [15] | BELCHER D P, ROGERS N C.Theory and Simulation of Ionospheric Effects on Synthetic Aperuture Radar[J]. IET Radar, Sonar and Navigation, 2009, 3(5):541-551. |
| [16] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Extracting Precise Atmospheric Propaganda Delays from Multiple Refrence Station GPS Networks[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4):523-528. (张宝成,欧吉坤,袁运斌,等.多参考站GPS网提取精密大气延迟[J].测绘学报,2012, 41(4):523-528.) |
| [17] | AKIRA I, YASUGO K, LIU J. Ionospheric Effects on SAR at 100MHz to 2GHz[C]// Proceedings of IGARSS. Seattle: IEEE, 1998: 475-477. |
| [18] | LIU J, KUGA Y, ISHIMARU A. Ionospheric Effects on SAR Imaging: a Numerical Study[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(5): 939-947. |
| [19] | ZILINSKAS M S, TAMOSIUNAITE M. Yearly, Seasonal and Daily Variations of Radio Refractivity[J]. Acta Physica Polonica A, 2011, 119 (4): 533-536. |
| [20] | NORLAND R.Temporal Variation of the Refractive Index in Coastal Waters[C]//Proceedings of SPIE. Wuhan: Society of Photo Optical, 2006:1-4. |
| [21] | JIAO Peinan. Radar Environment and Propagation Characteristics[M]. Beijing: Electronic Industry Press, 2007. (焦培南. 雷达环境和电波传播特性[M]. 北京:电子工业出版社,2007.) |
| [22] | HUO Xingliang, YUAN Yinbin, OU Jikun, et al. Daily, Half-yearly Variation and Winter Anomaly Phenomena of Ionospheric TEC in China by Means of GPS[J]. Progress in Natural Science, 2005, 15(5): 626-630. (霍星亮,袁运斌,欧吉坤,等. 基于GPS资料研究中国区域电离层TEC的周日变化、半年度及冬季异常现象[J].自然科学进展,2005, 15(5):626-630.) |
| [23] | KOU Leilei, WANG Xiaoqing, XIANG Maosheng. Effect of Orbital Errors on Geosynchronous Circular SAR Imaging and Interferometric Processing[J]. Journal of Zhejiang University Science, 2011, 12(5):404-416. |
| [24] | ZHU M, WADGE G, Holley R J. High-resolution Forecast Models of Water Vapor over Mountains: Comparison with MERIS and Meteosat Data[J]. IEEE Geoscience and Remote Sensing Letter, 2007, 4(3): 401-405. |
| [25] | BRUNO D, HOBBS S E. Radar Imaging from Geosynchronous Orbit: Temporal Decorrelation Aspects[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7):2924-2929. |