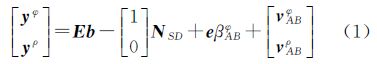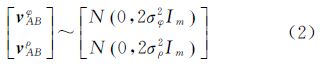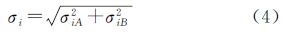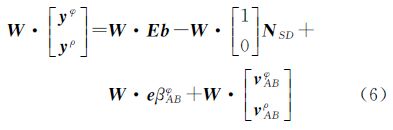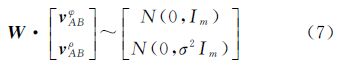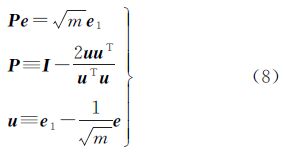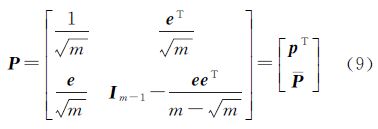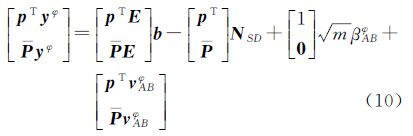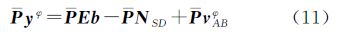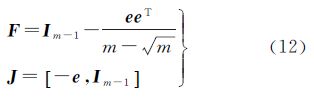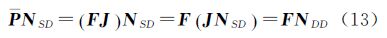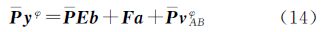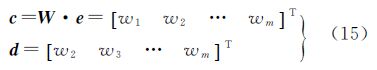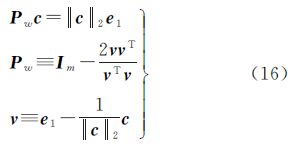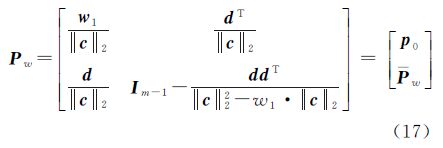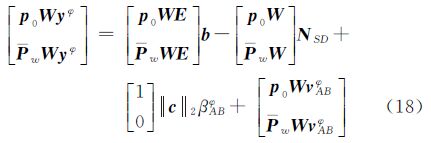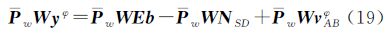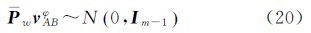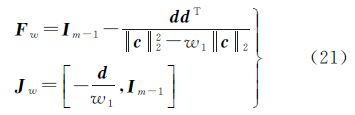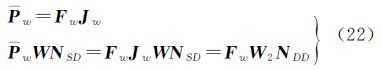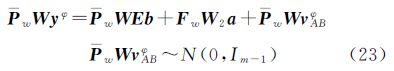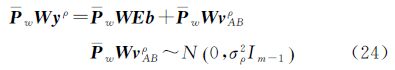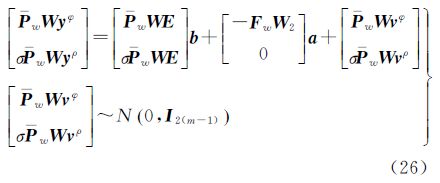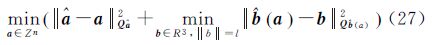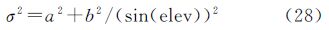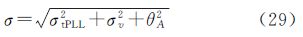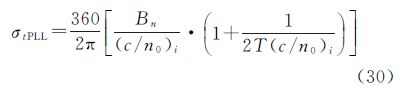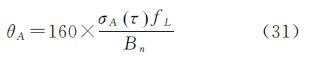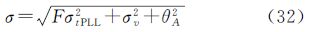2. 中央党校数字图书馆,北京 100091
2. Digital Library of Party School of the Central Committee of C.P.C, Beijing 100091, China
随着GPS的发展,基于GPS 载波相位测量的高精度载体姿态测量技术取得了瞩目的进展[1, 2, 3]。利用GPS信号进行姿态测量具有体积小、成本低、无累积误差等优势,已经成为当前姿态测量的主要手段之一。相对于多历元定姿算法,单历元定姿算法具有避免周跳检测和修复的优势,成为当前工程应用的研究热点[4, 5, 6]。文献[1]对约束方法进行了改进,加速了模糊度搜索过程;文献[2]在求解浮点解的过程中利用Householder变换,使得双差观测方程去相关;文献[3]根据多组基线的关系,改进了解算模型。
在定姿算法中,最为关键的是整周模糊度N的计算。文献[7]提出的利用基于基线长度约束的LAMBDA(least squares ambiguity decorrelation adjustment)算法是求解整周模糊度的一种有效算法[7, 8, 9]。文献[10]结合姿态角约束,使用金字塔算法提高了整周模糊度求解效率;文献[11]提出一种适合实时姿态测量的模糊度解算方法,它利用单差平滑伪距进行解算,其解算速度远快于上述方法,并且计算量很小;文献[12]利用排序和双Cholesky分解对滤波得到的模糊度进行降相关处理,并结合收缩模糊度搜索空间的思想来搜索固定整周模糊度。
在实际运用中,由于单历元观测方程冗余度小,在卫星数量少、仰角低、信号弱的情况下,载波相位精度低会使得解算成功率降低。因此如何提高成功率已成为单历元解算的主要问题。在卫星数目不多且有低仰角卫星的情况下,低载噪比的观测值的使用,会降低整周模糊度解算成功率;采用直接剔除低载噪比卫星降低了定姿系统的可靠性。鉴于此,本文对卫星的载波相位精度进行分析,提出加权矩阵,利用加权最小二乘,有效地利用载噪比高的卫星信息,从而提高了模糊度解算的可靠性和稳定性,使得姿态解算成功率有所提高。
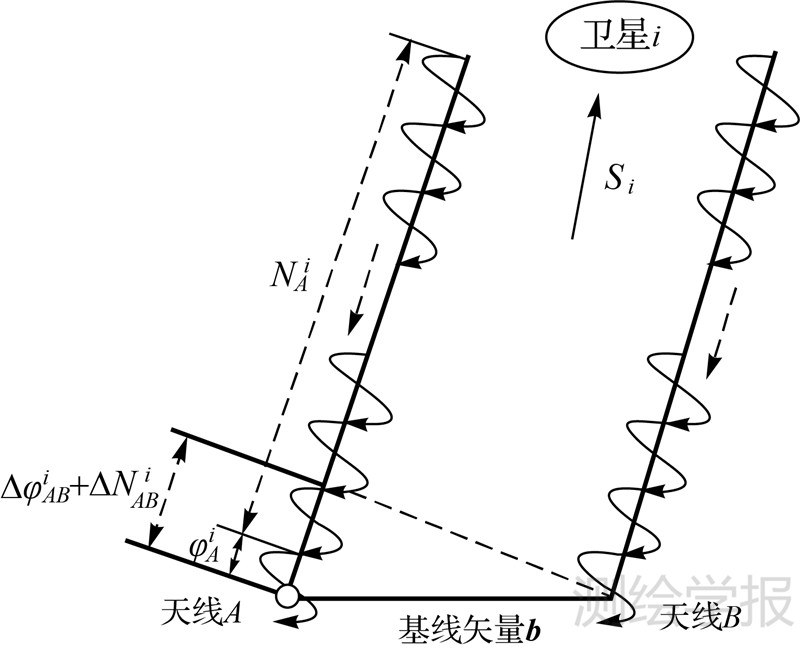
2 基本数学模型 2.1 数学模型图 1为短基线求解基线矢量的数学观测模型。
|
| 图 1 短基线定姿数学模型 Fig. 1 The mathematical model of short baseline attitude determination |
以A、B为端点的天线接收卫星信号,观测量主要包括时间、载波相位和码信息。在短基线定姿数学模型中,基线矢量见图 1中的b。由于基线长度远小于卫星到接收机的距离,可建立卫星i的单差载波相位观测和码观测方程,联立得[7]
式中,yφ=[ΔφAB1,ΔφAB2,…,ΔφABm]T,ΔφABi为A、B两天线到卫星i的单差载波相位的小数部分;yρ=[ΔρAB1,ΔρAB2,…,ΔρABm]T,ΔρABi为A、B两天线到卫星i的单差码观测量;NSD=[ΔNAB1,ΔNAB2,…,ΔNABm]T,为单差模糊度向量,ΔNABi为待估计的单差整周模糊度;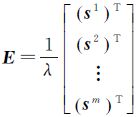 ,为接收机到卫星的设计矩阵,其中,si为天线到卫星i的单位矢量;λ为载波波长; 本文采用GPS的L1信号,λ=0.190 3 m。b为基线向量;e=[1 1 … 1]T;βABφ为两接收机钟差;vABφ=[ΔvAB1φ ΔvAB2φ … ΔvABmφ]T,为载波观测噪声;vABρ=[ΔvAB1ρ ΔvAB2ρ … ΔvABmρ]T,为码观测噪声。
,为接收机到卫星的设计矩阵,其中,si为天线到卫星i的单位矢量;λ为载波波长; 本文采用GPS的L1信号,λ=0.190 3 m。b为基线向量;e=[1 1 … 1]T;βABφ为两接收机钟差;vABφ=[ΔvAB1φ ΔvAB2φ … ΔvABmφ]T,为载波观测噪声;vABρ=[ΔvAB1ρ ΔvAB2ρ … ΔvABmρ]T,为码观测噪声。
噪声统计模型为
上述的定姿基本数学模型为等精度单差观测模型。但在实际情况中,接收机不同通道接收的卫星载波和码精度有一定差别,即单差观测噪声vABi的统计分布并不是对角线相等的2σφ2。当该历元的某些观测卫星的相位观测值存在较大的误差时,有时可能导致单历元模糊度搜索失败。为了提高单历元定位的成功率和精度,可以进一步考虑不同卫星的相位观测值权重。本文提出加权矩阵,将基本模型改进为加权单差数学模型。精度高的观测值取得高权重,精度低的观测值取得低权重,使信号差的卫星对定姿的影响尽量最小。
2.2 加入权值的数学模型加权模型,即对不同观测量设定一个权重。对于不同的卫星,可根据其卫星高度角、载噪比等特性确定其观测误差。考虑载波观测方程,卫星i的权重为wi,将其定义为单差载波相位yφ的测量误差标准差σi的倒数,即
式中,yφ=[ΔøAB1 ΔøAB2 … ΔøABm]T,且A、B两天线独立。设σiA、σiB为A、B天线接收到卫星i的载波相位误差标准差,可得
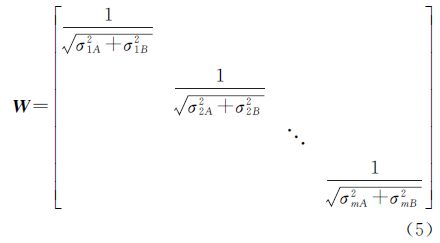
本算法是以m颗卫星的单差观测方程为基本模型,加入权重后,仍以单差方程为起点通过Householder变换,进行双差降相关处理。各个接收通道互不相关,因此加入的权重矩阵为对角阵。这样,在单差方程中加入的对角阵权重,相比在双差方程中的权重,避免了相关性,形式更加明了直接、易理解。在m颗卫星的单差模型中,权重矩阵W为m阶对角阵
假定同一通道载波精度与码精度比值一定,码方程同样可利用以上权重矩阵W。利用权重矩阵W对数学模型式(1)进行加权,表达式如下
噪声统计特性为
引入权重矩阵W,提高了卫星信号好的观测值权重,降低了卫星信号差的观测值权重,使得整周模糊度的浮点解具有更高的精度。
3 姿态的解算在求解以A、B为端点的载体姿态过程中,最为关键的是整周模糊度N的计算。首先通过最小二乘估计,可以得到整周模糊度的浮点解,文献[5, 6, 7]对于浮点解的计算作出改进工作,本文基于此思路引入加权,解算浮点解。其次由基于基线约束的CLAMBDA算法变换搜索空间,固定整周模糊度,进而完成基线解算[13],最终得到载体的姿态角。
3.1 原始模型求解浮点解根据模型式(1),进行双差运算,利用最小二乘,求解浮点解。但由于码观测方差和载波相位观测方差相差悬殊,导致搜索效率不高。文献[14]对直接求解双差模型进行改进:提出利用单差方程和Householder变换,削减钟差项βABφ,再通过矩阵变换得到双差整周模糊度向量。
基本思路为:考虑基本数学模型(1),定义Householder转换矩阵P∈Rm×m,Householder向量为u,满足
式中,e、e1形式固定,e=[1 1 … 1]T,e1=[1 0 … 0]T;m为卫星数目。分解P矩阵有 式中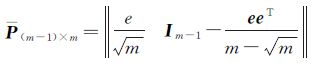
将式(1)两边同乘以P矩阵,即有
经过分解后P矩阵的变换,仅有第一个方程含有钟差项。将式(10)中不含钟差项的部分提取出来,可得到消除种差项的观测方程
式(11)得到了基本模型的载波相位单差方程。求解双差方程的过程中,对P(m-1)×m进行分解变换,定义双差转换矩阵F∈R(m-1)×(m-1),J∈Rm×m,满足
可以证明P=FJ
选取仰角最高的卫星为参考星,根据单差和双差整周模糊度的关系
容易得出
定义a=-NDD,通过式(13),可将式(11)变换如下
式(14)为定姿基本模型的双差载波观测方程。通过Householder变换,不仅消除了钟差项,并且使得双差观测量不相关。改进后的加权模型,同样根据文献[14]的思路,利用Householder变换对单差方程进行处理,最终得到定姿双差观测方程。
3.2 改进模型求解浮点解引入权重矩阵后,根据Householder变换性质[14, 19],推导过程如下,定义权重向量c、d满足
定义Householder转换矩阵Pw∈Rm×m,Householder向量v,满足
式中,e、e1形式固定,e=[1 1 … 1]T,e1=[1 0 … 0]T,||c||2=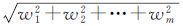 ,wi为式(3)所定,则有
式中,Pw=
,wi为式(3)所定,则有
式中,Pw=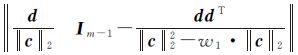 。
。
考虑加权后的载波相位单差方程,将改进模型式(6)中的载波方程两边同乘以转换矩阵Pw,即有
提取式(18)中不含钟差项的部分
Householder变换不改变噪声的统计特性
引入权重后,对比原有算法的式(12),定义双差转换矩阵Fw∈R(m-1)×(m-1),Jw∈Rm×m
容易证明
式中,设模糊度次权重矩阵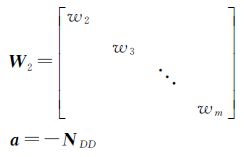
对于码观测方程,同理可得
定义载波和码观测值标准差比值σ
式中,σφ、σρ分别表示载波和码观测值的标准差,整理式(23)和式(24)可得[15, 16]对比式(14),加权后模型得到了不同精度载波相位和码的双差观测方程。根据此方程,利用最小二乘可得基线矢量b、模糊度a的浮点解和相应的协方差矩阵[12];在约束条件||b||=l基线长度为已知条件下,通过下式的估计目标函数来求得模糊度的固定解
加权后得到基线矢量与整周模糊度的浮点解。根据文献[17, 18],利用基于基线约束的CLAMBDA算法,搜索固定整周模糊度。CLAMBDA算法由无约束的LAMBDA算法发展而来,可以大大缩减搜索范围,提高搜索效率,是目前较有效的搜索算法。对于刚性载体,固定的整周模糊度和基线矢量,可以确定载体的姿态。
4 权重矩阵W的计算对于加权算法,根据2.2节分析可知,权重W是加权的关键和重点。在定姿系统中,观测量为载波相位和码,根据式(3)—(5)式可知,载波精度决定加权模型中的权重矩阵W。文献[21, 22]利用经验值的卫星高度角进行加权是目前使用较为广泛的方法,利用高度角为变量对观测值的方差进行估计如下
式中,elev为卫星高度角;a、b为经验值,a=4 mm,b=3 mm。但是在高仰角卫星被遮挡、多径严重的情况下,卫星的高度角不能用来衡量信号质量,尤其是载波相位精度。载噪比C/N0是载波信号能量与噪声能量在1 Hz带宽上的比值,它与多径效应、接收天线增益等有关。相较于高度角,载噪比更加直接地反映了接收机所接收到的卫星载波信号质量。近几年,许多GPS接收机都能输出载噪比观测值,这为基于载噪比加权模型的推广应用提供了可能。因此本文提出利用载噪比对定姿系统进行加权的新模型。下面从载波精度理论模型和实际测得的载波精度进行分析对比,得出权重矩阵W。
4.1 载波精度理论模型载波相位精度,主要取决于GPS接收机的PLL相位误差。PLL相位误差包括相位颤动和动态应力误差。在静态情况下,只考虑相位颤动。相位颤动是每个不相关的相位误差源平方和的平方根,主要包括热噪声和振荡器噪声。如式(29)[22]
式中,σtPLL为热噪声;σv为由振动引起的振荡器颤动;θA为由阿仑偏差引起的振荡器颤动,在此以度为单位进行分析。(1) σtPLL:热噪声是相位的主要误差源,计算公式如下
式中,Bn为噪前带宽,对于GPS L1信号,Bn=15 Hz;T为相干积分时间T=0.001 s ;(c/n0)i为相应天线接收到的卫星i的载噪比。由式(30)可得,载波精度与载噪比关系为,载噪比越大,精度越高。(2) σv:由振动引起的振荡器颤动。
用户运动和接收装置的机械颤动会引起接收机基准振荡频率的抖动,相应的相位抖动误差大致在2°左右。
(3) θA:由阿仑(Allan)偏差引起的振荡器颤动。
由于阿仑型晶体振荡频率漂移随着时间的累积也会引入相位抖动噪声,σA(τ)为阿仑偏差,是指在时间段为τ的频率稳定度,τ表示阿仑偏差测量值的短期稳定度闸门时间,单位为秒,以阿仑偏差为参量的相位噪声的3阶环经验公式见式(31)
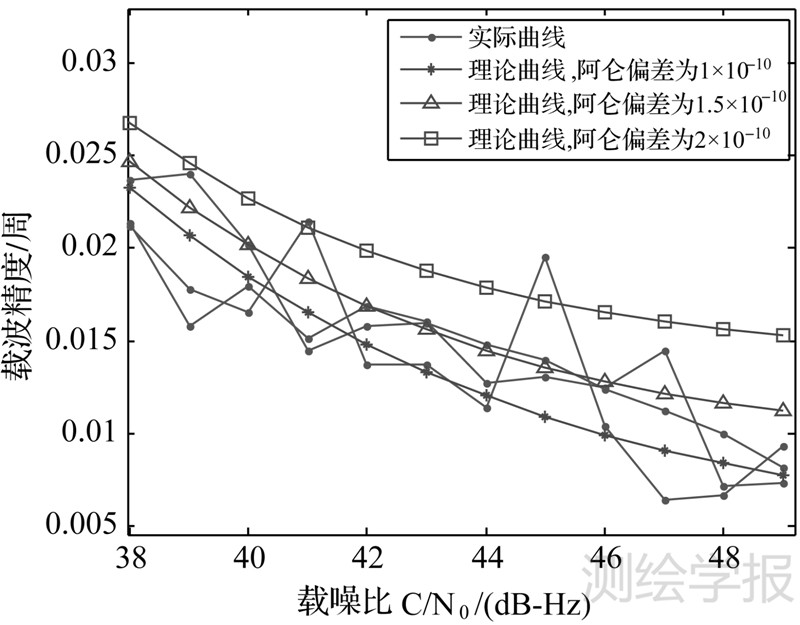
式中,fL为载波L1频率;Bn为噪前带宽。 4.2 理论与实际曲线对比矫正为了验证本试验平台的载波测量精度,进行了零基线试验。零基线试验是指两个接收机同时接收同一副天线的数据,通过两接收机载波相位单差得到载波噪声。本试验OEM板为NovAtel 公司的SuperStar II,12通道,L1单频C/A接收机。本文分析载噪比38~49 dB-Hz区间内,载波精度的变化。
因为热噪声是相位的主要误差源,为了更好地利用载噪比的权重,实际中将式(29)改进如下
式中,F为热噪声的权重。实际得到的结果与理论曲线对比如图 2所示。
|
| 图 2 载噪比与载波精度关系,理论与实际曲线 Fig. 2 The theory and actual curve of the relationship between carrier to noise ratio and the accuracy of carrier phase |
结果表明热噪声权重F=8,阿仑偏差σA(τ)=1×10-10时,与实际曲线更吻合。将阿仑偏差和权重值代入式(31)、式(32),可得到载波相位精度,进而得到加权权重系数W。
5 实际数据仿真和测试为了比较原有算法和改进后算法在成功率方面的差异,本文进行了3组单频单历元的定姿试验。数据采集地点选取空旷高地,基线长度为1 m,每组试验处理1500历元,通过Matlab 7.8平台仿真得到姿态结果。为了验证利用载噪比进行加权的算法优势,本文同时进行了高度角加权算法的解算,参考式(28)的高度角加权方法。
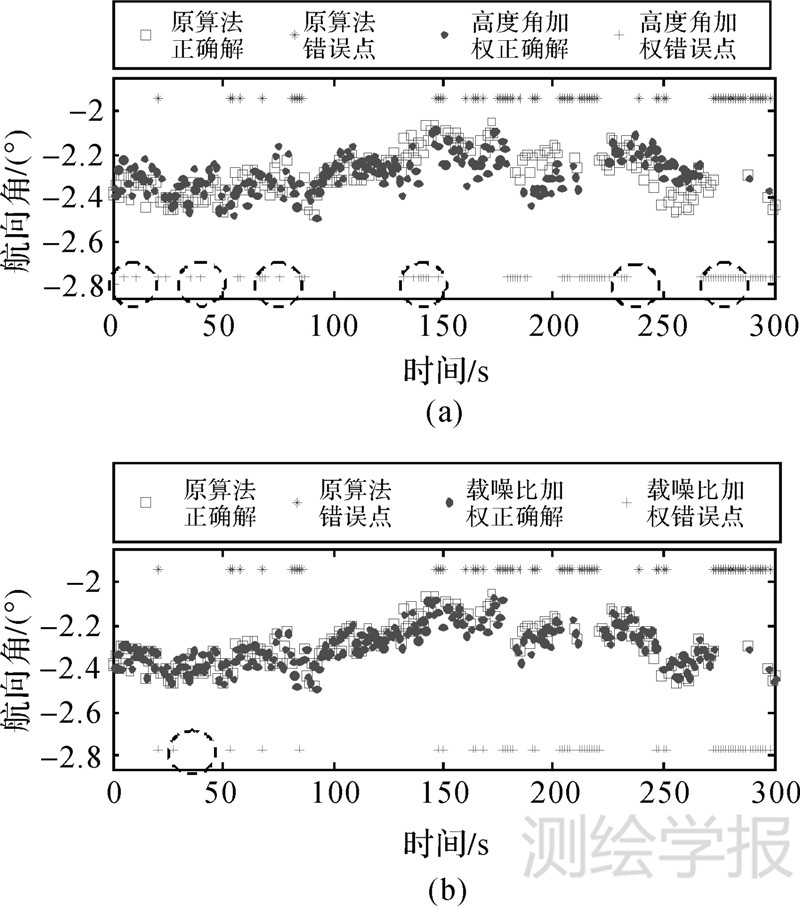
为了更清晰地展示改进后的试验效果,每组以300历元为例,得到以下几组航向角结果对比,见图 3。
|
| 图 3 第1组原有算法和高度角加权,原有算法和载噪比加权算法对比图 Fig. 3 The first comparison of original algorithm and elevation weighted algorithm,original algorithm and CN0 weighted algorithm |
3组试验,每组1500历元的成功率统计结果见表 1。
| 序号 | 原有算法/(%) | 加权算法/(%) | 提高/(%) | |
| 1组 | 66.00 | 高度角加权 | 71.60 | 5.60 |
| 载噪比加权 | 72.67 | 6.67 | ||
| 2组 | 58.40 | 高度角加权 | 76.93 | 18.53 |
| 载噪比加权 | 78.93 | 20.53 | ||
| 3组 | 52.73 | 高度角加权 | 58.07 | 5.34 |
| 载噪比加权 | 60.60 | 7.87 | ||
根据图 3,得到如下结论:
(1) 高度角加权算法和载噪比加权算法在一定程度上都提高了姿态解算的成功率。经过加权后,试验结果的错误点明显减少。
(2) 载噪比加权相比于高度角加权更加稳定。在一些数据段(如图 3中,1—100历元数据),原有未加权算法能够解算正确的点,利用高度角加权,反而无法搜索到正确的整周模糊度。即在这些数据段利用高度角加权相对于原有的未加权算法,解算成功率反而下降。而相同数据段,改进后的利用载噪比加权算法基本不会出现此类情况。这意味着,在实际应用中,高度角加权存在使成功率降低的风险,而载噪比加权可以避免这种情况,载噪比加权方法姿态解算的稳定性更高。
(3) 载噪比加权不会影响正确解的情况。原有未加权算法的正确点与载噪比加权算法正确点基本重合;而高度角加权后正确点相较于未加权偏移较大,解算精度低。图 3中150—250历元,图 3(a)的高度角加权和图 3(b)的载噪比加权方法对比明显,高度角加权正确点偏移较大,载噪比加权重合度高。
根据试验成功率表 1可得到,载噪比加权算法提高了姿态解算的成功率。原有的未加权算法对卫星载噪比低的卫星没有采取有效措施,改进算法通过加权,使精度高的卫星信息得以充分利用。从表格数据可以看出,加权方法可以使成功率提高5个以上百分点,第2组数据提高达20个百分点,提升效果显著。相比于高度角加权算法,载噪比加权使成功率提高幅度更大,比高度角加权提高1~2个百分点。
通过图表的对比可看出,载噪比加权方法不仅提高了姿态解算的成功率,而且相比于高度角加权的方法,解算成功率更高,稳定性更强。
6 总 结GPS单频单历元定姿系统对环境要求高,在卫星数量少、载噪比低等情况下,成功率较低。本文以载噪比和载波精度为出发点,对原算法进行改进。根据不同卫星载波精度的差异,提出加权矩阵(提高了高精度观测值的权重,降低了低精度观测值的权重),建立加权模型,得到了更高精度的浮点解,提高了姿态解算成功率。
一般而言,低高度角的信号误差比较高的高度角信号误差要大,但是在高仰角卫星被遮挡、多径严重的情况下,高度角无法反映卫星信号的真实情况。载噪比作为衡量卫星信号强弱的重要标准,相对于高度角,更加可靠地反映了卫星的信号质量,更加精确地反映了对定姿系统起关键作用的载波精度。试验结果表明,对比于原有的未加权算法和高度角加权方法,本模型和算法提高了单频单历元姿态解算的成功率,提高了系统的可靠性和稳定性。
| [1] | WANG B, LING J M. A Constrained LAMBDA Method for GPS Attitude Determination [J]. GPS Solutions, 2009, 13(2):97-107. |
| [2] | QIN H L, CHEN W T. Performance Analysis and Improved Method for Single Epoch, Single Frequency Attitude Determination Using GPS [J]. Journal of PLA University of Science and Technology, 2011, 12(5):431-435. |
| [3] | COIAS J, SANGUINO J, OLIVEIRA P. Attitude Determination Using the Ambiguity Filter with Single-frequency L1 GPS Receivers[C]//Proceedings of Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing. [S.l.]:IEEE,2012: 1-8. |
| [4] | TEUNISSEN P J G. Least-squares Estimation of the Integer GPS Ambiguities[C]//General Meeting of the International Association of Geodesy. Beijing: [s.n.], 1993. |
| [5] | TEUNISSEN P J G. A New Method for Fast Carrier Phase Ambiguity Estimation.Proc. of IEEE Position [C]//Location and Navigation Symposium. Las Vegas:[s.n.],1994:562-573. |
| [6] | GABRILGE G,TEUNISSEN P J G. Testing a New Multivariate GNSS Carrier Phase Attitude Determination Method for Remote Sensing Platforms [J]. Advances in Space Research,2010(46):118-129. |
| [7] | PARK C,TEUNISSEN P J G. A Baseline Constrained LAMBDA Method for an Integer Ambiguity Resolution of GNSS Attitude Determination System [J].IEICE Transaction on Communication, 2008,83(6):587-594. |
| [8] | BUIST P J. Multivariate Bootstrapped Relative Positioning of Spacecraft Using GPS L1/Galileo E1 Signals [J]. Advances in Space Research, 2011, 47(5):770-785. |
| [9] | TEUNISSEN P J G. Integer Least-squares Theory for the GNSS Compass [J].Journal of Geodesy, 2010,84:433-447. |
| [10] | LIU Zhijian. Algorithm of a Real-time Attitude System Using Non-dedicated GPS Receivers [J]. Acta Geodaetica et Cartographica Sinica, 2005,34(3):213-217.(刘志俭.一种基于非专用接收机的GPS实时定姿算法[J].测绘学报,2005,34(3):213-217.) |
| [11] | PENG Xiaogang. A Real-time Integer Ambiguity Resolution Algorithm for GPS Attitude Determination [J]. Bulletin of Surveying and Mapping,2011(5):16-19.(彭晓刚.一种实时GPS 姿态测量中的整周模糊度的解算方法[J].测绘通报,2011(5):16-19.) |
| [12] | LIU Ning. An Algorithm for Rapid Integer Ambiguity Resolution in Single Frequency GPS Kinematical Positioning [J]. Acta Geodaetica et Cartographica Sinica, 2013,42(2):211-217.(刘宁.单频GPS动态定位中整周模糊度的一种快速解算方法[J].测绘学报, 2013,42(2):211-217.) |
| [13] | PAUL D J, CHRISTIAN T. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects [M].Amsterdam:Delft Geodetic Computing Centre,1996. |
| [14] | CHANG X W, PAIGE C C, YIN L.Code and Carrier Phase Based Short Baseline GPS Positioning: Computational Aspects [J].GPS Solutions, 2004, 7(4):230-240. |
| [15] | CHANG X W, PAIGE C C.An Orthogonal Transformation Algorithm for GPS Positioning[J].SIAM Journal on Scientific Computing,2003,4:1710-1732. |
| [16] | REMONDI B W. Using the Global Positioning System Phase Observable for Relative Geodesy [D].Austin:The University of Texas at Austin, 1984:124-132. |
| [17] | TEUNISSEN P J G.The LAMBDA Method for the GNSS Compass [J]. Artificial Satellites, 2006, 41(3):89-103. |
| [18] | CHANSIK P, TEUNISSEN P J G.Integer Least Squares with Quadratic Equality Constrain and Its Application to GNSS Attitude Determination Systems[J]. International Journal of Control,Automation and Systems, 2009, 7(4):566-576. |
| [19] | GOLUB G H, LOAN C F.Matrix Computations [M].Baltimore:The Johns Hopkins University Press, 1996:206-222. |
| [20] | GEORGE P G.A Comparison of Four Methods of Weighting Double Difference Pseudo-range Measurements[J]. Australian Surveyor,1995,40(4):60-66. |
| [21] | WIESER A, BRUNNER F K. An Extended Weight Model for GPS Phase Observations [J]. Earth Planets Space, 2000(52):777-782. |
| [22] | KAPLAN E D,HEGARTY C J. Understanding GPS Principles and Application[M]. 2nd ed. Beijing: Publishing House of Electronic Industry Press, 2007:134-140.(GPS 原理与应用[M]. 第2版. 北京:电子工业出版社,2007:134-140.) |