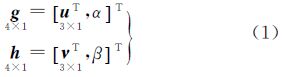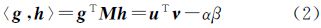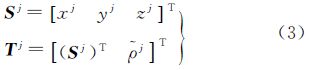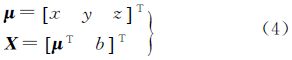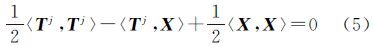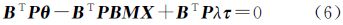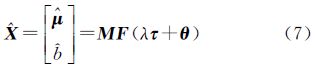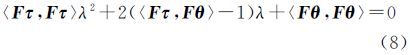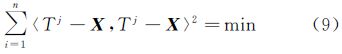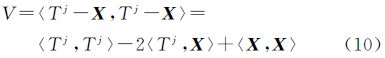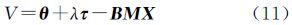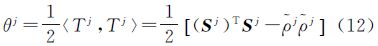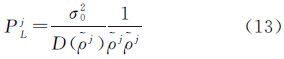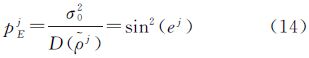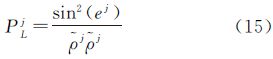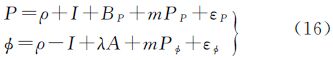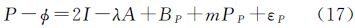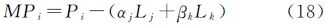1 引 言
我国正在实施的北斗卫星导航系统(BeiDou navigation satellite system,BDS)已经可以实现我国及周围区域导航定位功能[1],但由于卫星数量有限,精度不高,使其在应用中大大受限。确定合适的GPS随机模型能有效控制对流层及多路径误差的影响,提高定位精度[2]。1996年,文献[3]利用载波的信噪比提出sigma-ε模型。1998年,文献[4]提出以卫星高度角来确定GPS观测值的权比方法。研究表明对流层延迟与多路径效应都随着卫星高度角的增大而减少,该方法便于程序设计,易于工程实现,得到了广泛的应用。Bernese从4.2版本开始应用此方法[5]。上述随机模型都是针对GPS设计,且不能通过严密的公式推导获得。GPS由24颗中圆地球轨道(MEO)卫星组成,而北斗导航系统空间星座包括地球静止轨道(GEO)、倾斜地球同步轨道(IGSO)和中圆地球轨道(MEO)卫星[1, 6]。不同种类卫星高度差异较大,当卫星高度角相同时,卫星高度可能不一样,仅仅以卫星高度角定权显然不再准确。
目前单点定位算法一般都是基于传统的泰勒级数展开,将观测方程线性化,用泰勒级数展开计算[7]。针对GPS伪距单点定位观测方程求解的非线性问题,文献[8]于1985年提出一种称为“闭合求解”的全局性非线性最小二乘算法(Bancroft算法),这是一种不需要迭代、具有代数解析性的直接解算方法[9],在计算上有效且数值稳定[10, 11, 12]。
为了解决上述观测值定权问题,本文将Bancroft算法应用到北斗导航系统单点定位中,通过Lorentz内积方程推导权矩阵,得到一种新的北斗导航系统观测值定权公式。为了验证此公式,借鉴了以往零/短基线分析导航卫星系统测距信号质量的思路[13, 14, 15],基于不同测站多天实测数据分析了北斗GEO、IGSO和MEO卫星测距信号及多路径效应的影响。结果表明新方法提高了北斗导航系统单点定位精度。
2 单点定位定权方法 2.1 Bancroft算法Bancroft算法主要依据R4维空间下的一种Lorentz内积。Lorentz内积的定义为,在R4维空间中有向量g、h∈R4,且
则向量g、h的Lorentz内积为根据Lorentz内积,将Bancroft算法应用于导航伪距观测方程。
定义卫星位置向量为
接收机位置向量为
式中,b=cδt表示接收机钟差等效距离;ρj表示消除卫星钟差、电离层、对流层延迟的伪距。在计算卫星位置时考虑地球自转的影响,直接改正卫星位置向量,则对于第j颗卫星有伪距方程对于每一个伪距观测值ρj和对应的卫星位置向量Sj,均可根据式(5)列出一个Lorentz内积方程。设在某一历元观测到d(d≥4)颗卫星,则可给出此时Lorentz内积方程组
式中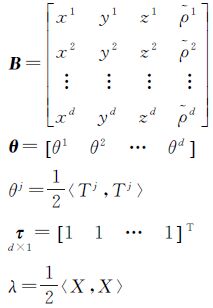
在式(6)中,P为伪距观测值的对称权阵[16],可解出基于Bancroft算法的待定未知参数
式中,F=(BTPB)-1BTP为B的广义逆;未知参数λ可由以下二次方程解出 2.2 推导权矩阵从文献[10]可以看出,Bancroft是根据Lorentz内积准则求得的Lorentz范数全局非线性最小二乘解,可将式(8)看作Lorentz内积形式下的全局非线性最小二乘算法,其目标函数为
误差方程为 将B、θ、τ代入可得传统的方法是直接利用伪距观测量的先验信息作为确定权矩阵的依据,这在利用线性最小二乘求解时是严密的[16]。但是当伪距观测方程转换为Lorentz内积方程时,需重新推导Lorentz内积误差方程的权矩阵。由式(11)可将θ看成虚拟观测值
根据误差传播定律,Lorentz内积误差方程的权为
式中,σ02为单位权中误差;D(ρj)表示方差。设第j颗卫星高度角为ej,由文献[4]中以卫星高度角来确定观测值权比的方法可得此卫星伪距观测值的权为
结合式(14)可得,Lorentz内积误差方程的权为
对比式(15)与式(14)可知,新的定权公式在以卫星高度角定权的基础上考虑了卫星至接收机的距离因素,针对不同种类卫星高度差异较大的特点作出了改进。
3 北斗测距信号分析北斗的伪距和相位方程均可表示为
式中,P和Φ分别为伪距和相位观测;ρ为与频率无关项;BP为硬件延迟;I为电离层斜延迟;mPP、mPΦ分别为伪距和相位多路径误差;A为含初始相位偏差的模糊度参数;λ为波长因子;εP、εΦ分别表示两类观测值的观测噪声,且满足E{ε}=0。由式(16)可导出如下两类组合观测值,用以分析测距信号质量[13, 15]。
(1) 伪距相位差值组合(code-minus-phase combination,CC组合),具体形式为
(2) MP组合,利用北斗三频观测值可单独考察对应于频段i的伪距多路径误差,具体形式为
式中,i、j、k为北斗三频相位观测值的频段,且i≠j≠k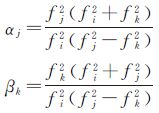
显然,αj+βk=1。此组合消去了几何距离和电离层延迟的影响[17]。
为了消除以上两式所含的非零期望值,文献[13, 14, 15]提出了低阶多项式拟合和历元间差分的方法。试验证明,针对高频观测值,对CC和MP组合实施历元间差分,可消除模糊度常数,并大大消弱电离层延迟、多路径误差和伪距硬件延迟。本文直接采用历元间差分法。
4 算例分析与比较 4.1 单点定位定权方法分析笔者试验分析了4个地区(乌鲁木齐、喀什、昆明、长春)的多频北斗静态观测数据,观测时间为2012-10-07-2012-10-21,采样间隔为1s,测站坐标为已知值。本文选取2012-10-07乌鲁木齐站的数据进行分析,其他测站及观测时间处理结果与之类似,不再给出。
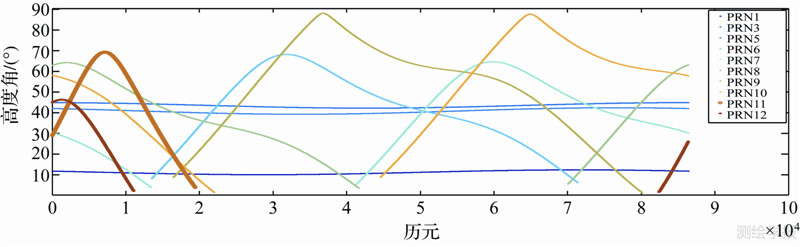
在数据处理中笔者采用以下3种方案进行单点定位解算:方案1采用最小二乘法求解,各伪距观测值用卫星高度角定权;方案2采用Bancroft算法求解,各卫星观测值用卫星高度角定权;方案3采用Bancroft算法求解,各卫星观测值用本文推导的公式定权。由于下文CC及MP组合需要使用载波相位观测值,在数据预处理中,利用北斗三频周跳探测方法[18, 19, 20]剔除了有粗差的数据并标记周跳位置。图 1为试验数据采集过程中可观测到的卫星的高度角,表 1分析了各历元MEO卫星的可视情况。图 2及表 2为3种方案RMS对比。
|
| 图 1 乌鲁木齐站卫星高度角 Fig. 1 El of CWUQ |
| MEO卫星数量 | 历元 |
| 2 MEO卫星 | 1~10983 |
| 1 MEO卫星 | 10984~19435 |
| 82412~86400 | |
| 无 MEO卫星 | 19436~82411 |
|
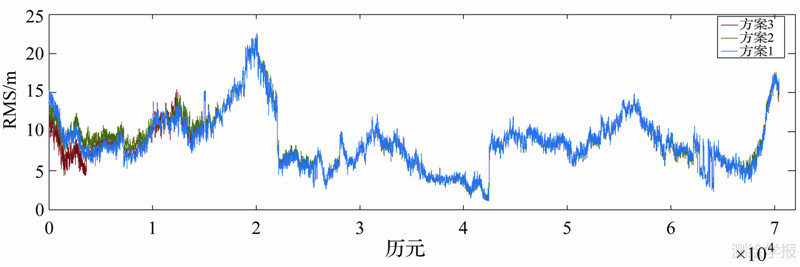
| 图 2 3种方案RMS对比 Fig. 2 RMS of three schemes |
| 方案 | 无MEO卫星历元RMS | 1颗MEO卫星历元RMS | 2颗MEO卫星历元RMS |
| 方案1 | 10.537 | 16.632 | 8.388 |
| 方案2 | 10.377 | 16.188 | 7.799 |
| 方案3 | 10.393 | 15.974 | 5.933 |
通过对以上图表的对比分析,可以得出如下结论:
(1) 北斗导航系统目前已能提供较高精度的单点定位服务,各种方案都能达到25m以下的单点定位精度。
(2) 结合图 2及表 2可知,方案3的定位精度与其他方案对比有所提高。这说明在Bancroft算法中依据Lorentz内积方程推导出的定权公式要比利用卫星高度角定权更为严密、准确,能够得到更高的精度。
(3) 结合表 1及表 2可知,在没有观测到MEO卫星的历元,3种方案定位精度相当。在观测到1颗或2颗卫星的历元,方案3精度好于其他方案,并且MEO卫星数量越多,单点定位精度提升越明显。
为了进一步分析上述现象,选取第1个和第15000个历元列出详细信息见表 3。其中定权方案1、2分别为直接利用高度角定权和利用本文公式定权,单点定位算法都采用Bancroft算法。
| 第1个历元 | 第15000个历元 | |||||||||||
| PRN | 卫星类型 | 高度角/(°) | 高度/km | 定权方案1 | 定权方案2 | PRN | 卫星类型 | 高度角/(°) | 高度/km | 定权方案1 | 定权方案2 | |
| 1 | GEO | 11.9 | 35770 | 0.012 | 0.008 | 1 | GEO | 11.3 | 35807 | 0.014 | 0.012 | |
| 3 | GEO | 45.0 | 35780 | 0.143 | 0.107 | 3 | GEO | 42.5 | 35796 | 0.164 | 0.162 | |
| 5 | GEO | 42.2 | 35793 | 0.129 | 0.095 | 5 | GEO | 40.3 | 35782 | 0.15 | 0.148 | |
| 7 | IGSO | 30.5 | 35707 | 0.074 | 0.052 | 6 | IGSO | 41.2 | 35739 | 0.156 | 0.154 | |
| 8 | IGSO | 62.9 | 35853 | 0.227 | 0.178 | 7 | IGSO | 39.4 | 35881 | 0.145 | 0.141 | |
| 10 | IGSO | 58.2 | 35720 | 0.206 | 0.162 | 9 | IGSO | 62.8 | 35766 | 0.284 | 0.301 | |
| 11 | MEO | 28.9 | 21599 | 0.067 | 0.118 | 10 | IGSO | 29.5 | 35875 | 0.087 | 0.081 | |
| 12 | MEO | 45.0 | 21589 | 0.143 | 0.280 | |||||||
| RMS | - | - | - | 9.73 | 6.67 | RMS | - | - | - | 6.19 | 6.60 | |
从表 3中可以看出在第15000个历元只观测到GEO和IGSO卫星,其卫星高度相当,测站与卫星距离差别较小,两种定权方案变化较小,故其定位精度也相当。对比可知第1个历元可观测到GEO、IGSO和MEO卫星,MEO卫星与其他卫星高度差异较大,新的定权公式考虑了距离因素,其定权结果与直接利用高度角定权的结果相比变化较大,提高了单点定位精度,更为准确。本文定权公式优势主要体现在导航系统星座较为复杂,导航卫星轨道高度差异较大时,随着北斗系统的建设,MEO卫星的增加,精度会有进一步的提升。
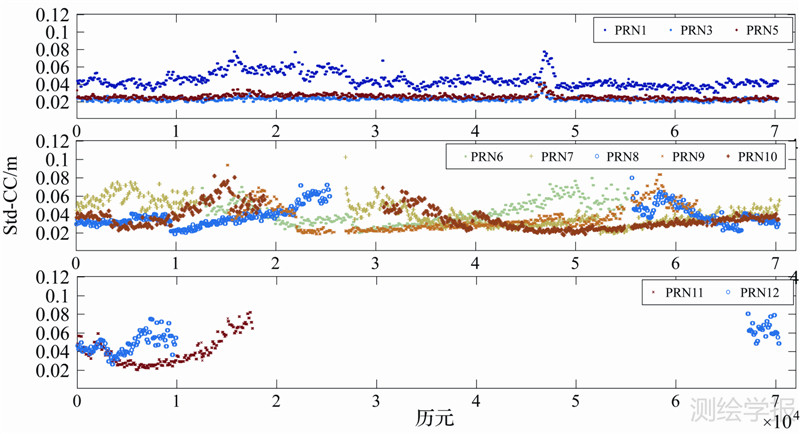
4.2 CC组合分析伪距观测噪声为了分析北斗测距信号观测噪声,按每组120个历元对CC组合观测值分组并计算伪距标准差,图 3给出了北斗GEO、IGSO和MEO卫星的伪距标准差。
|
| 图 3 北斗卫星伪距标准差 Fig. 3 STD-CC of BDS satellites |
由图 3可得出以下结论:
(1) GEO卫星伪距标准差较为稳定,约为0.02m。其中PRN1号卫星伪距标准差较大,结合图 1可以看出整个观测过程中其卫星高度角都在12°左右。
(2) MEO和IGSO卫星伪距标准差较GEO卫星较大,且与卫星高度角相关,文献[15]也报告了类似的试验结果。可能原因是GEO卫星相对于测站是“静止的”,而IGSO和MEO卫星是运动的,可能存在多普勒效应。值得注意的是,在本文试验数据预处理中,GEO卫星几乎没有周跳,而IGSO和MEO卫星周跳、粗差较多,这也从一定程度上反映了GEO卫星数据质量较好。
(3) 虽然不同种类卫星伪距标准差略有差别,但北斗导航卫星伪距标准差基本都在0.1m以下。由表 1及表 2可以看出新的算法精度提高在米级,表 2中第1个历元达到了3m。所以可以得出观测时间段内北斗各卫星伪距观测噪声虽略有差异,但噪声标准差数值较小,对单点定位精度影响有限,不是新算法精度提高的主要原因。
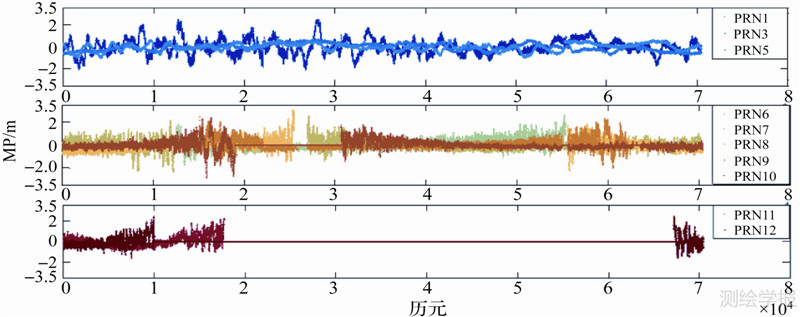
4.3 MP组合分析伪距多路径效应为了分析伪距多路径效应对北斗单点定位精度的影响,利用三频观测值提取并改正了多路径效应。改正后的伪距使用方案2与方案3方法解算,分别为方案4和方案5。试验数据为上文可观测到MEO卫星的前10000个历元(图 4、表 4)。
|
| 图 4 北斗卫星多路径误差 Fig. 4 MP of BDS satellites |
| m | ||||
| 方案 | N | E | U | RMS |
| 方案4 | 2.64698 | 1.71431 | 8.91068 | 9.45228 |
| 方案5 | 1.94729 | 1.30762 | 7.51683 | 7.87430 |
结合图 4与表 4可得出以下结论:
(1) 北斗卫星伪距多路径效应存在明显的周期性,与卫星轨道周期相关,GEO卫星呈现低频变化,而IGSO、MEO卫星呈现高频变化。
(2) 结合表 2与表 3,可以看出多路径效应改正后,不同方案单点定位精度都有所提高。
(3) 对比方案4、方案5可以看出经过多路径效应改正后,新的定权公式仍能提高北斗单点定位精度。
5 结 论本文将全局性非线性最小二乘算法(Bancroft算法)应用到北斗导航系统中。针对其星座复杂、不同种类卫星高度差异较大的特点,重新推导了Bancroft算法的定权公式,基于伪距相位差值组合(CC组合)观测值分析了北斗GEO、IGSO和MEO卫星的测距信号质量,基于多路径组合(MP组合)观测值分析了伪距多路径效应对单点定位的影响。结果表明:
(1) 北斗导航系统中,GEO卫星测距信号优于IGSO、MEO卫星。
(2) 当同时观测到GEO、IGSO、MEO卫星时,MEO卫星高度与其他卫星差异较大,新的定权公式考虑了距离因素,较好地解决北斗导航系统卫星观测值定权问题,明显提高了单点定位精度,有一定的实用价值。
(3) 北斗卫星导航系统中伪距多路径效应影响较为严重。GEO卫星的伪距多路径效应呈现低频变化,IGSO和MEO卫星呈现高频变化,可利用北斗三频组合观测值来提取并改正多路径误差。经过多路径误差改正后,新的定权公式仍能提高北斗单点定位精度。
随着GNSS的发展以及我国北斗卫星导航系统的建设,多模GNSS数据融合导航体现出了优势,如何将本文算法应用到不同导航系统及融合导航中值得进一步研究。
| [1] | YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1):1-5.(杨元喜. 北斗卫星导航系统的发展、贡献与挑战[J]. 测绘学报,2010,39(1):1-5.) |
| [2] | OZLUDEMIR M T. The Stochastic Modeling of GPS Observations[J]. Turkish Journal of Engineering and Enviornmental Sciences, 2004, 28: 223-231. |
| [3] | WARD P W, BETZ J W, HEGARTY C J. GPS Satellite Signal Characteristics[C]// Understanding GPS: Principles and Applications. Boston: Artech House Publishers, 1996: 83-117. |
| [4] | ROTHACHER M, SPRINGER T A, SCHAER S, et al. Processing Strategies for Regional GPS Networks[C] // Advances in Positioning and Reference Frames: IAG Scientific Assembly. London: Springer, 1998: 93-101. |
| [5] | BEUTLER G, BROCKMANN E, FANKHAUSER S, et al. Bernese GPS Software Version 4.0[R]. Bern: University of Bern, 1996: 1-46. |
| [6] | China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document[R]. Beijing: China Satellite Navigation Office, 2011. (中国卫星导航系统管理办公室. 北斗卫星导航系统(空间信号接口控制文件)[R]. 北京: 中国卫星导航系统管理办公室, 2011.) |
| [7] | XU G C. GPS Theory: Algorithms and Applications[M]. 2nd ed. Berlin: Springer-Verlag, 2007: 39-40. |
| [8] | HUANG Sixun, SHENG Zheng. The New Algorithm for Stand-alone Positioning with Global Positioning System and Numerical Experiments[J]. Acta Physica Sinica, 2006, 55(12): 6720-6726. (黄思训,盛峥. 一种全球定位系统接收机单点定位的新算法及数值实验[J]. 物理学报, 2006, 55(12): 6720-6726.) |
| [9] | BANCROFT S. An Algebraic Solution of the GPS Equations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1985, 20(1): 56-59. |
| [10] | ZHANG Qin. Research on Nonlinear Least Square Theory and Its Applications in GPS Positioning[D]. Wuhan: Wuhan University, 2002:138-144. (张勤. 非线性最小二乘理论及其在GPS定位中的应用研究[D]. 武汉: 武汉大学, 2002: 138-144.) |
| [11] | ZHANG Q, TAO B Z, ZHAO C Y, et al. Nonlinear Filter Method of GPS Dynamic Positioning Based on Bancroft Algorithm[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2005, 22(2): 170-176. |
| [12] | YANG Yuanxi, ZHANG Shuangcheng, GAO Weiguang. Analyses and Comparisons of Some Strategies for Nonlinear Kalman Filter in GPS Navigation[J]. Engineering of Surveying & Mapping, 2005, 14(3): 4-7. (杨元喜,张双成,高为广. GPS 导航解算中几种非线性Kalman滤波的理论分析与比较[J]. 测绘工程,2005,14(3): 4-7.) |
| [13] | BAKKER P F D, MAREL H V D, TIBERIUS C C J M. Geometry-free Undifferenced, Single and Double Differenced Analysis of Single Frequency GPS, EGNOS and GIOVE-A/B Measurements[J]. GPS Solutions, 2009, 13(4): 305-314. |
| [14] | HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et al. Characterization of Compass M-1 Signals[J]. GPS solutions, 2012, 16(1): 117-126. |
| [15] | CHENG Pengfei, LI Wei, BEI Jinzhong. Precision Analysis of BeiDou Range Measurement Signals[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 690-695. (程鹏飞,李伟,秘金钟. 北斗导航卫星系统测距信号的精度分析[J]. 测绘学报, 2012, 41(5): 690-695.) |
| [16] | RUAN Rengui, HAO Jinming. Improvement of Bancroft Algorithm[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 87-90. (阮仁桂,郝金明. 对Bancroft算法的改进[J]. 大地测量与地球动力学, 2008, 28(5): 87-90.) |
| [17] | MA X Y, SHEN Y Z. Multipath Analysis of COMPASS Triple Frequency Observations[R]. Xi’an: GPS/GNSS 2012, 2012: 1-13. |
| [18] | LI Jinglong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Un-differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6):717-722. (李金龙,杨元喜,徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722.) |
| [19] | HUANG Lingyong, SONG Lijie, WANG Yan, et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. (黄令勇,宋力杰,王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报,2012, 41(5): 763-768.) |
| [20] | LIU Xuchun, WU Yue, ZHANG Zhenglu, et al. Application of GPS Triple-frequency Data in Detection and Repair of Cycle Slip and Gross Error[J]. Journal of China Coal Society, 2006, 31(5): 585-588. (刘旭春, 伍岳, 张正禄, 等. GPS三频数据在周跳和粗差探测与修复中的应用[J]. 煤炭学报, 2006, 31(5): 585-588.) |