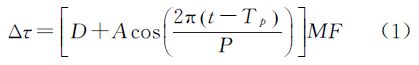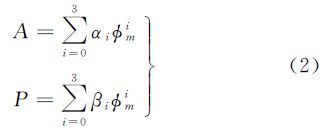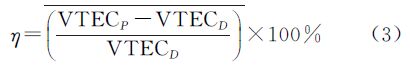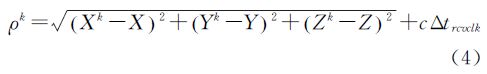2. 北京卫星导航中心,北京 100094
2. Beijing Navigation Center, Beijing 100094, China
电离层延迟作为导航计算的误差源之一,严重影响着用户的定位精度[1, 2, 3]。对于单频用户,需要依靠导航系统发播的电离层模型参数进行相应的电离层延迟改正,其精度受用户所处位置和发播模型精度所限。许多国内外学者都分析讨论了电离层监测及电离层延迟的建模方法[4, 5, 6, 7, 8],其中Klobuchar模型是单频用户最常使用的电离层延迟改正模型之一[9]。
GPS用户市场主要使用单频接收机[3]。单频用户使用的电离层模型即为Klobuchar模型。该模型有8个参数,这些参数是地面控制系统根据当天为一年中的第几天(将一年分为37个区间)以及前5天太阳的平均辐射强度,从370组常数中选取的[10, 11],其全球改正精度约为50%~60%[12]。在此基础上,我国学者提出了14参数的Klobuchar模型,其精度在中国区域明显优于GPS发播模型,可以达到70%以上,应用于我国区域卫星导航系统[13, 14, 15]。目前遍布全球的GPS测站可以获得高精度的全球电离层监测结果,为电离层演化与建模研究提供了重要支撑,为什么GPS不采用全球的观测数据拟合参数发播给用户呢?
本文针对这一问题进行了分析研究。首先对欧洲定轨中心(center for orbit determination in Europe,CODE)预报的全球电离层图(global ionosphere maps,GIM)进行精度评估;其次利用预报电离层图进行Klobuchar模型参数拟合;然后采用IGS提供的高精度GIM对不同模型的参数改正精度进行分析;最后分别将拟合得到的模型参数与GPS发播的参数应用到单点定位以比较其对单频用户定位和授时的影响。
2 Klobuchar模型GPS卫星导航电文中发播的Klobuchar模型参数在设计时综合考虑用户计算的复杂度和改正精度,发播α0—α3、β0—β3共8个参数。夜晚将电离层延迟设置为5×10-9 s的平场,白天将电离层延迟建模为本地时的余弦函数,见式(1)[15, 16]
式中,MF为投影函数;余弦函数的幅度A用与α参数和穿刺点地磁纬度øm相关的三阶多项式表示;余弦函数的周期P用与β参数和穿刺点的地磁纬度øm相关的三阶多项式表示,见式(2)[15, 16] 3 Klobuchar参数拟合与改正精度分析 3.1 COPG电离层精度分析CODE根据IGS约200个GPS/GLONASS测站和其他机构的数据生成全球电离层图GIM,可以作为电离层垂直总电子含量VTEC的参考值。GIM产品给出了地理纬度87.5°S—87.5°N,间隔2.5°;180°W—180°E,间隔5°;时间间隔为2 h的电离层VTEC分布[1]。因为要采用全球观测数据解算,所以高精度的GIM文件一般至少会延迟3 d提供,命名为CODG文件。
CODE还提供了根据CODG文件拟合得到的Klobuchar-style电离层模型参数。因其是事后得到的,不能作为预报模型参数发播。
CODE同时提供根据历史数据预报的全球GIM,命名为COPG文件,可以对两天后的全球电离层进行预报。利用COPG和事后较为精密的CODG文件比较,可以估计COPG的预报精度。定义平均相对误差为
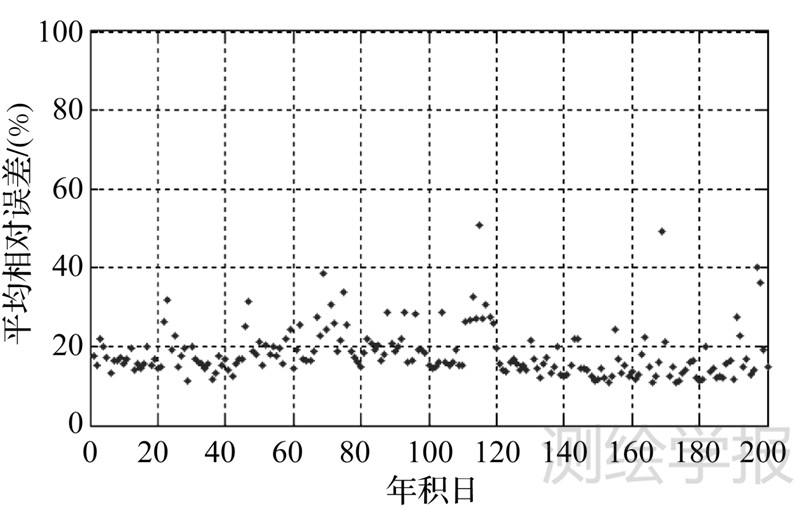
式中,VTECP为COPG文件给出的VTEC值;VTECD为CODG文件给出的VTEC值;当预报值与事后计算值均小于9 TECU时,不参与统计。2012年年积日1—200每日的COPG文件平均相对误差统计结果如图 1所示,平均相对误差均值为18.31%,即平均预报精度为81.69%。图 1中平均相对误差大于35%的3月9日、4月24日、6月17日、7月15日都发生了中等及以上规模的地磁暴现象,导致COPG文件预报电离层电子含量的精度有所下降。
3.2 Klobuchar 参数拟合方法根据COPG文件,可以拟合出Klobuchar模型8参数,以下称为K8-FIT1参数。因为COPG文件是预报文件,所以K8-FIT1参数可以作为预报模型参数发播,其拟合过程如下:
(1) 将全球不同地点按照地磁纬度划分,每3°分为一个区域,共划分60个区域,按地磁纬度编号。
(2) 将COPG文件中的VTEC值按照上述要求划分,分为60组,并将每个点的地方时转化为UT时。
(3) 将每一组内的数据建模为Klobuchar模型的模式,即夜间为固定值,白天为余弦函数,每组得到一个最优的余弦函数的振幅A和周期P。
(4) 利用60组A值和P值,以地磁纬度为自变量,采用最小二乘法拟合出Klobuchar模型参数中的4个振幅参数α和4个周期参数β。
下文中提到的纬度均为地磁纬度。
|
| 图 1 COPG文件平均相对误差 Fig. 1 Average relative error of COPG files |
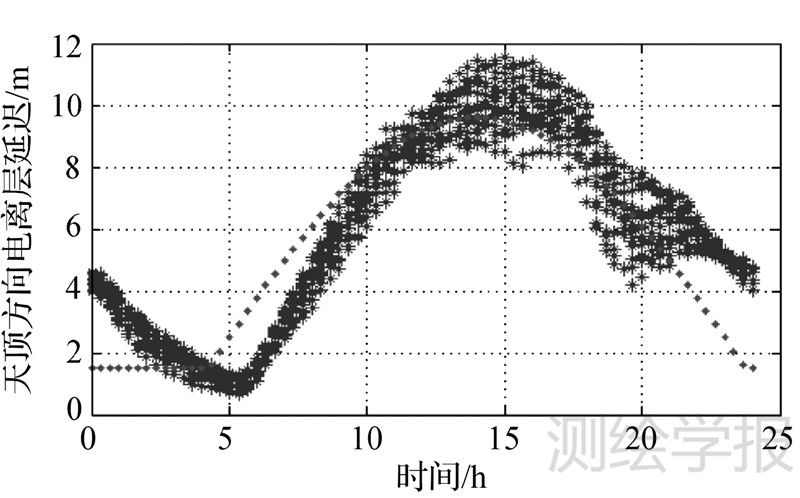
以2012年年积日100日为例,图 2给出了地磁纬度-1.5°—1.5°的拟合情况,其中星形组成的线为根据GIM计算得到的天顶方向的电离层延迟,点线为根据延迟值拟合的模型结果。图 3和图 4分别给出了不同模型参数振幅A和周期P随地磁纬度的分布情况。
|
| 图 2 2012年年积日100的拟合情况 Fig. 2 2012 DOY 100 fitting result |
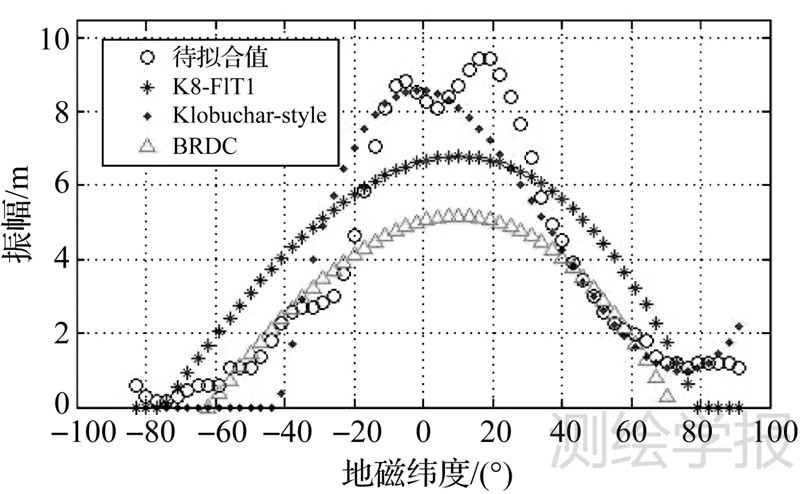
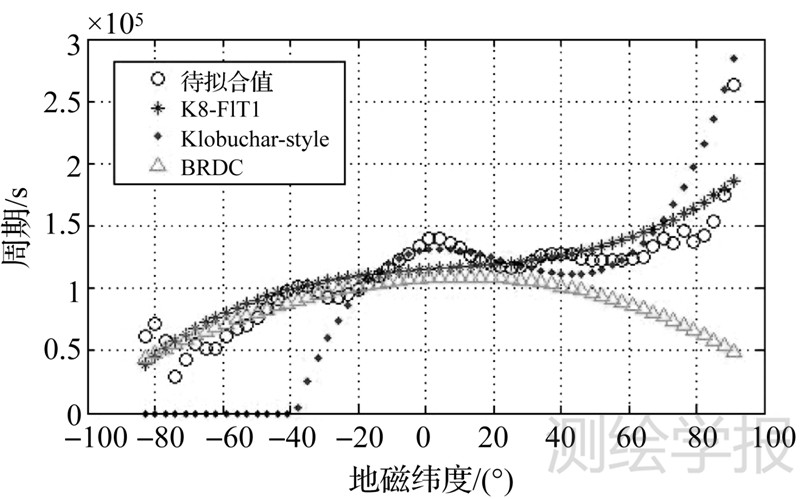
图 3和图 4中,圆圈、星形、圆点和三角形组成的线分别表示3.2节(4)中参与拟合模型参数的60个区域的振幅值A和周期值P、利用K8-FIT1参数的计算值、利用CODE提供Klobuchar-style参数的计算值和利用GPS广播星历文件中提取参数的计算结果。
|
| 图 3 2012年年积日100的K8-FIT1振幅拟合情况 Fig. 3 2012 DOY 100 K8-FIT1 amplitude fitting result |
|
| 图 4 2012年年积日100的K8-FIT1周期拟合情况 Fig. 4 2012 DOY 100 K8-FIT1 period fitting result |
从图 3和图 4可以看出,CODE提供的Klobuchar-style参数没有采用南半球高纬度地区的数据,对北半球和南半球低纬度地区有较好的改正效果,但在南半球高纬度地区不能进行改正。K8-FIT1参数由于利用了全球数据,因此与Klobuchar-style数据有一定差异,而与GPS广播参数较为接近。
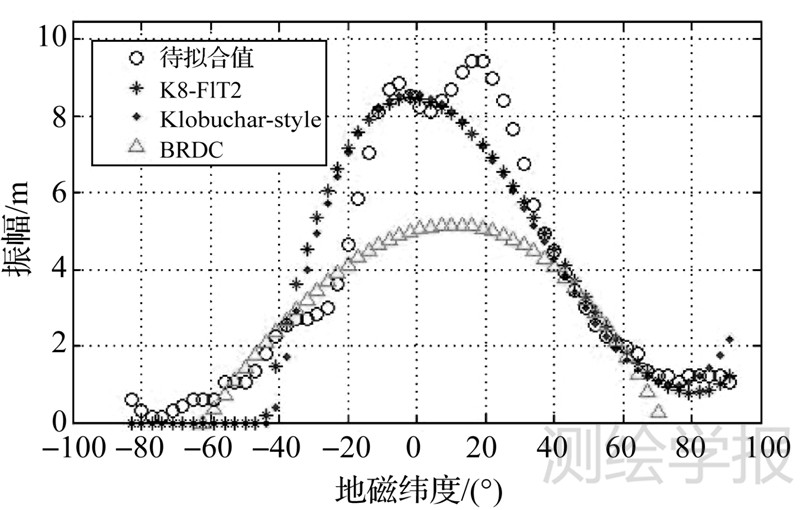
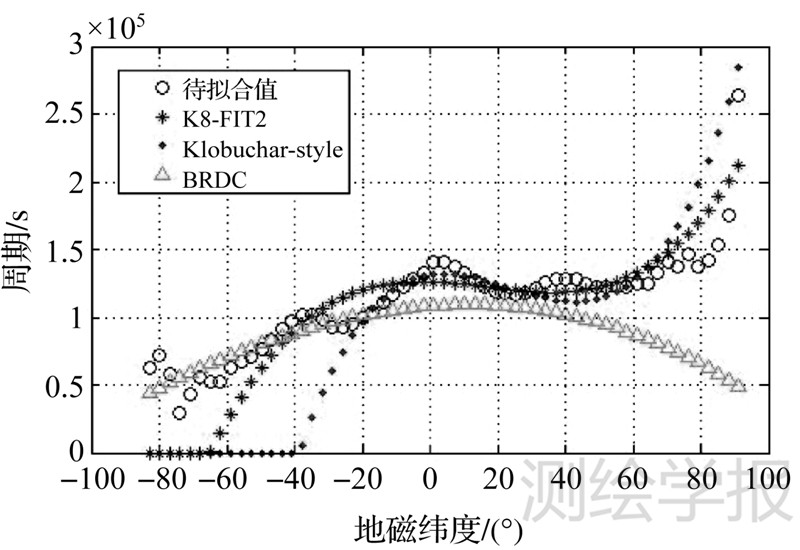
下面仅利用45°S以北的数据进行参数拟合,结果如图 5和图 6所示。以下称这种方法为K8-FIT2。从图中可以看出,采用预报文件拟合得到的K8-FIT2与CODE采用事后高精度电离层图得到的Klobuchar-style参数具有很高的一致性。
|
| 图 5 2012年年积日100的K8-FIT2振幅拟合情况 Fig. 5 2012 DOY 100 K8-FIT2 amplitude fitting result |
|
| 图 6 2012年年积日100的K8-FIT2周期拟合情况 Fig. 6 2012 DOY 100 K8-FIT2 period fitting result |
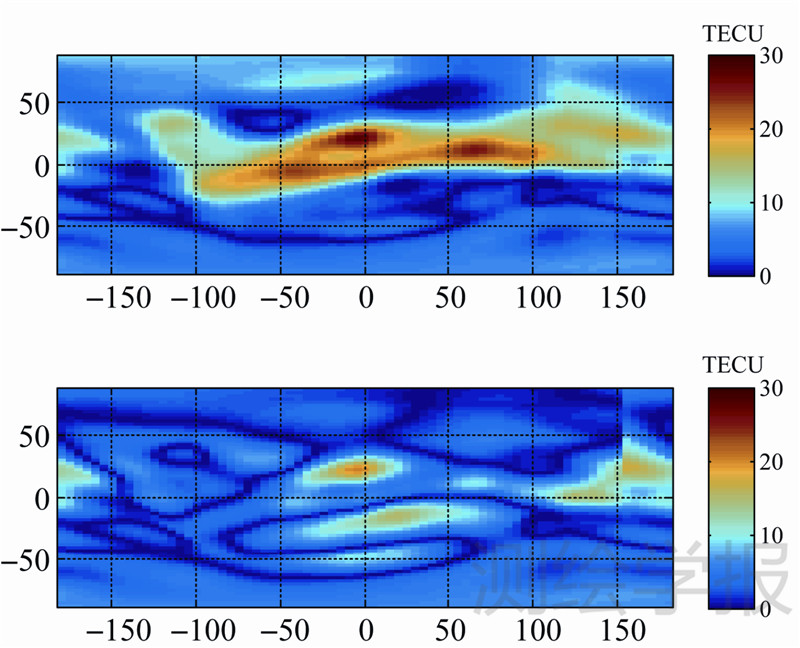
以2012年年积月151日UT14时为例,以IGS提供的事后高精度全球电离层图为参考,计算GPS广播的电离层模型参数与K8-FIT2参数的改正误差,结果如图 7所示。
|
| 图 7 2012年年积日151时,使用不同参数的Klobuchar模型的平均误差 Fig. 7 2012 DOY 151 mean error of Klobuchar model with different parameters |
从图 7中可以看出,采用GPS广播的电离层模型参数,全球平均改正误差为6.87 TECU;采用K8-FIT2参数,全球平均改正误差为3.98 TECU。在赤道附近和北半球,采用K8-FIT2参数的电离层延迟改正效果明显优于广播参数。
表 1给出了以IGS提供的事后高精度全球电离层图为参考,2012年3—6月不同模型参数的全球电离层平均改正精度。表中K-S为后处理的Klobuchar-style参数,其余3种为预报参数。从表 1可以看出,改正精度由高到低依次为K-S、K8-FIT2、K8-FIT1、GPS发播的导航电文中的电离层参数。
| (%) | ||||
| BRDC | K8-FIT1 | K8-FIT2 | K-S | |
| 改正精度 | 54.1 | 57.6 | 66.2 | 68.5 |
综上,即使采用全球电离层图文件拟合的K8-FIT1参数,也只与GPS发播参数的电离层延迟改正近似相当。这说明在不修改模型的情况下,使用全球数据进行参数拟合不能进一步大幅提升模型的改正精度。放弃45°S以南的数据,模型改正精度明显提升,这是因为振幅值表示为如式(2)所示的三次多项式,不能很好地刻画其随地磁纬度的变化情况(如图 3,低纬度地区拟合值偏低,高纬度地区拟合值偏高)。但仅利用北半球和南半球低纬度地区数据进行拟合,其幅值变化的三阶多项式拟合误差较小,因此可以明显提升这些区域内电离层延迟的改正精度。
4 不同电离层模型参数对定位和授时的影响4.1 定位结果分析
用户使用电离层延迟模型是为了提升其定位和授时精度,本文对单频用户采用不同电离层延迟模型参数的定位和授时结果作进一步分析。本文随机选取了位于南北半球的部分IGS测站的实测数据(测站位置信息详见表 2),分析其伪距单点定位的结果。根据卫星PRN号和观测历元,寻找最优广播星历计算卫星位置,根据钟差参数计算卫星钟差,采用Saastamoinen模型计算对流层延迟改正,相对论改正和地球自转改正均采用模型计算[17, 18, 19, 20]。对于电离层延迟改正分别采用不同的电离层模型参数进行计算。
| (°) |
| 测站名 | lat | lon | alt |
| tro1 | 69.662 719 | 18.939 649 | 138.105 3 |
| brew | 48.131 523 | -119.682 63 | 238.600 4 |
| bjfs | 39.608 601 | 115.892 49 | 87.464 5 |
| shao | 31.099 642 | 121.200 45 | 22.044 3 |
| twtf | 24.953 565 | 121.164 5 | 201.534 6 |
| pimo | 14.635 72 | 121.077 73 | 95.536 |
| ntus | 1.345 801 4 | 103.679 96 | 75.383 9 |
| areq | -16.465 516 | -71.492 797 | 2 488.928 6 |
| alic | -23.670 114 | 133.885 52 | 603.251 5 |
| sydn | -33.780 83 | 151.150 28 | 85.613 |
| mobs | -37.829 407 | 144.975 34 | 40.592 7 |
| vbca | -38.700 769 | -62.269 228 | 60.847 5 |
| hob2 | -42.804 709 | 147.438 74 | 41.063 8 |
| palm | -64.775 089 | -64.051 120 | 31.099 7 |
假设某历元观测到第k颗卫星的伪距观测量扣除卫星钟差、电离层延迟、对流层延迟、相对论改正和地球自转改正后的观测量表示为ρk,则
式中,第k颗卫星的位置用Xk,Yk,Zk表示;测站坐标用X,Y,Z表示;接收机时钟相对于系统时的超前用Δtrcvclk表示;c为光速。单点定位即根据单历元的至少4颗卫星的观测数据估计测站坐标和接收机钟差。本文采用最小二乘法进行平差单点定位解算。 表 3给出了电离层平静的5月30日的定位平均误差结果。| m |
| 测站 |
|
| tro1 | 2.91 | 2.78 | 2.09 | 1.66 | 2.18 |
| brew | 1.72 | 2.68 | 3.12 | 2.38 | 3.08 |
| bjfs | 2.35 | 3.05 | 4.00 | 3.63 | 2.56 |
| shao | 2.18 | 3.08 | 3.38 | 3.37 | 2.29 |
| twtf | 2.57 | 4.04 | 3.08 | 3.02 | 3.27 |
| pimo | 3.05 | 3.96 | 2.67 | 2.70 | 3.94 |
| ntus | 2.56 | 3.11 | 2.09 | 2.23 | 2.60 |
| areq | 2.28 | 3.29 | 2.17 | 2.31 | 2.76 |
| alic | 2.67 | 2.77 | 2.35 | 2.92 | 3.20 |
| sydn | 1.88 | 2.63 | 2.47 | 2.83 | 3.82 |
| mobs | 2.30 | 3.79 | 3.45 | 4.01 | 3.54 |
| vbca | 1.89 | 2.39 | 2.73 | 2.71 | 2.55 |
| hob2 | 2.37 | 3.07 | 2.74 | 3.35 | 2.79 |
| palm | 2.56 | 2.43 | 2.73 | 2.33 | 3.48 |
| 平均 | 2.38 | 3.08 | 2.79 | 2.81 | 2.97 |
从表 3可以看出,放弃了南半球高纬度数据的K8-FIT2和Klobuchar-style参数,相比GPS广播的模型参数,在北半球的定位精度并没有更好的表现,在南半球精度也基本相当,部分站改善,部分站变差,总体对定位解算影响不大。但为了进一步说明不同电离层模型参数对电离层延迟改正的影响,还需要对授时精度进行分析。
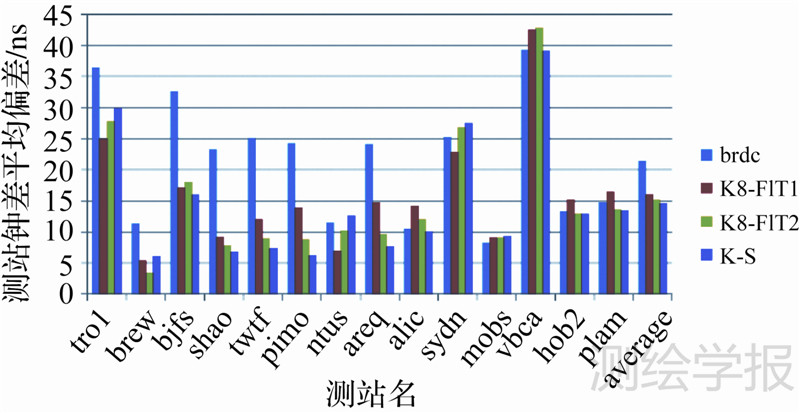
4.2 授时结果分析在定位解算中,未知量除了测站三维坐标,还有测站钟差。同一历元观测到所有卫星的共同误差将被吸收进站钟估计。以双频解算的站钟差为基准,5月30日不同电离层模型参数定位解算的站钟差误差如图 8所示。最后一列为对所有测站平均的结果。可以看出,测站钟差的精度从高到低依次为:事后的Klobuchar-style参数、K8-FIT2、K8-FIT1、GPS发播的Klobuchar参数,与不同参数电离层延迟改正精度顺序一致。
|
| 图 8 2012年5月30日,利用不同参数解算的各站钟差误差 Fig. 8 Deviation of station clock error calculated using different ionospheric model parameters in May 30,2012 |
上述结果表明,由于同一历元观测到所有卫星的电离层改正误差一部分被吸收进站钟估计,对定位影响较小。北半球和赤道附近测站,使用K8-FIT2参数明显提高了测站钟差精度,而南半球使用不同模型参数的精度基本相当,说明K8-FIT2参数在北半球和赤道附近对电离层延迟的改正明显优于GPS广播的Klobuchar模型参数和利用全球数据拟合的K8-FIT1参数。
为了分析电离层扰动条件下不同电离层模型参数的性能,笔者选取3月6日—3月12日(电离层扰动)和5月27日—6月2日(电离层平静)共计14 d的数据,计算上述14个测站的电离层平均改正误差、平均定位误差和站钟差误差,结果如表 4所示。
| BRDC | K8-FIT1 | K8-FIT2 | K-S | |
| 电离层平均改正误差/TECU | 7.95 | 7.14 | 5.82 | 5.51 |
| 定位平均误差/m | 3.47 | 3.38 | 3.33 | 3.35 |
| 站钟差平均误差/ns | 20.04 | 17.29 | 16.02 | 16.03 |
由表 4可知,虽然不同的电离层模型参数在电离层延迟改正效果上有明显不同,但对定位影响不明显,其原因是同一历元不同卫星的电离层模型改正误差与高度相关[21],其共同部分被吸收进站钟估计,因此影响授时精度,对定位影响不明显。以上分析说明,根据振幅值随地磁纬度的变化规律,有选择地使用部分区域数据进行拟合得到的参数提升了电离层模型的改正精度,从而提高了用户授时精度。
5 结 论本文根据CODE提供的预报全球电离层图COPG文件,设计了两种K8-FIT电离层模型参数拟合方案。K8-FIT1采用全球数据进行拟合,对电离层延迟的改正效果与GPS广播的电离层模型参数相当;K8-FIT2和事后的Klobuchar-style参数在拟合过程中放弃了南半球高纬度地区的数据,对电离层延迟改正精度有明显的提高。由于南半球陆地面积较少,测站也较少,这样的选择对于用户的实际使用是有一定意义的。但是用户定位授时分析结果表明,拟合过程中放弃南半球高纬度数据并没有明显提高北半球定位精度或者降低南半球高纬度地区定位精度,对定位结果的改善无明显贡献,但提升了用户的授时精度。
由于电离层是复杂多变的,简单地使用8个参数精确描述全球的电离层十分困难,即便利用全球电离层图文件拟合的K8-FIT参数相对于GPS广播参数,对定位精度也没有明显提升,但对测站钟差精度有明显改善。GPS采用离散的370组参数代替直接拟合参数的方法并没有对单频定位造成精度损失,可能是由于将部分误差吸收进了测站的钟差。
CODE提供的Klobuchar-style参数提供了一种提高单频用户电离层延迟改正精度的思路,但由于模型的限制,为了得到更好的定位结果,还需要研究更好的电离层改正模型或策略。
上面的单点定位过程中,使用的是广播电文中的星历和钟差参数,这也在定位中引入了不小的误差,对分析电离层延迟改正对定位误差的贡献情况有影响。下一步将利用IGS精密卫星星历和钟差进行定位解算,进一步分析电离层模型参数选取对定位的影响。
| [1] | HERNNDEZ-PAJARES M, JUAN J M, SANZ J, et al. The IGS VTEC Maps: A Reliable Source of Ionospheric Information Since 1998[J]. Journal of Geodesy, 2009, 83(11):263-275. |
| [2] | YU Ming, GUO Jiming, GUO Jingjun. Ionospheric Delay Values from Klobuchar Model and Dual Frequency Measurements: Comparison and Analysis[J]. Bulletin of Surveying and Mapping, 2004(6): 5-8. (余明,郭际明,过静珺. GPS电离层延迟Klobuchar模型与双频数据解算值的比较与分析[J]. 测绘通报, 2004(6): 5-8.) |
| [3] | RUAN Rengui, WU Xianbing, FENG Laiping, et al. Single-frequency Precise Point Positioning with Simultaneous Ionospheric Delay Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 490-495. (阮仁桂,吴显兵,冯来平,等. 同时估计电离层延迟的单频精密单点定位方法[J]. 测绘学报, 2012, 41(4): 490-495.) |
| [4] | JIN S G, LUO O F, PARK P. GPS Observations of the Ionospheric F2-layer Behavior during the 20th November 2003 Geomagnetic Storm over South Korea[J]. Journal of Geodesy, 2008, 82 (12): 883-892. |
| [5] | JIN S G, HAN L, CHO J. Lower Atmospheric Anomalies Following the 2008 Wenchuan Earthquake Observed by GPS Measurements[J]. Journal of Atmospheric and Solar-terrestrial Physics, 2011, 73: 810-814. |
| [6] | YUAN Yunbin, OU Jikun. A New Method on Ionospheric Delay Correction for Single Frequency GPS Users in WAAS[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(sup): 96-102. (袁运斌,欧吉坤. WAAS系统下单频GPS用户电离层延迟改正新方法[J]. 测绘学报, 2000, 29(sup): 96-102.) |
| [7] | XIANG Shulan, HE Xiaowei, MOU Qifeng. Research of Ionospheric Delay from Klobuchar and IRI Model[J]. Microcomputer Information, 2008, 1(6): 200-202. (向淑兰,何晓薇,牟奇锋.GPS电离层延迟Klobuchar与IRI模型研究[J].微计算机信息, 2008,1(6): 200-202.) |
| [8] | FAN Guoqing, WANG Wei, XI Xiaoning. Modeling of Ionosphere VTEC Using Generalized Regression Neural Network[J]. Acta Geodaetica et Cartographica Sinica, 2010,39(1):16-21. (范国清,王威,郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报,2010, 39(1):16-21.) |
| [9] | YUAN Y, HUO X, OU J, et al. Refining the Klobuchar Ionospheric Coefficients Based on GPS Observations[J]. IEEE Transaction on Aerospace and Electronic System, 2008,44(4):1498-1510. |
| [10] | LI Zhenghang, HUANG Jingsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005:52-58. (李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005:52-58.) |
| [11] | LI Zhenghang, ZHANG Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M].Wuhan: Wuhan University Press, 2009:58-63. (李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M]. 武汉:武汉大学出版社,2009:58-63.) |
| [12] | KLOUBUCHAR J A. Ionospheric Delay Algorithm for Single-frequency GPS Users[J]. IEEE Transaction on Aerospace and Electronic System, 1988,23(3): 321-331. |
| [13] | ZHANG Hongping. Study on GPS Based China Regional Ionosphere Monitoring and Ionosphere Delay Correction[D]. Shanghai: Shanghai Astronomical Observatory, 2006:66-86. (章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海:上海天文台, 2006:66-86.) |
| [14] | HUANG Yidan, WANG Mingyuan, HAN Ling, et al. Improvements on Klobuchar Model Based on Chinese Ionospheric Data[C]//Proceedings of the Nineteenth Conference of Chinese Society of Space Research. Ningbo:[s.n.],2006:759-766. (黄逸丹,王明远,韩玲,等. 基于中国电离层资料对Klobuchar模型的改进[C]//中国空间科学学会空间探测专业委员会第十九次学术会议.宁波:[s.n.],2006:759-766.) |
| [15] | WU Xiaoli, HU Xiaogong, WANG Gang. Evaluation of Compass Ionospheric Model in GNSS Positioning [J]. Advance in Space Research, 2012, 51(6): 959-968. |
| [16] | JORGENSEN P S. An Assessment of Ionospheric Effects on the User[J]. Journal of the Institute of Navigation, 1989, 36(2):195-204. |
| [17] | LIU Jingnan, YE Shirong. GPS Precise Point Positioning Using Undifferenced Phase Observation[J]. Geomatics and Information Science of Wuhan University, 2002,27(3): 234-240. (刘经南,叶世榕.GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报:信息科学版,2002, 27(3): 234-240.) |
| [18] | YI Zhonghai, CHEN Yongqi, ZHU Jianjun,et al.An Approach to Regional Real Time Precise Point Positioning Based on IGS Ultra-rapid Orbit[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(2):226-231. (易重海,陈永奇,朱建军,等.一种基于IGS超快速星历的区域性实时精密单点定位方法[J]. 测绘学报,2011, 40(2):226-231.) |
| [19] | WU Xiaoli, PING Jingsong, LIU Li,et al.Hardware Delay Solution of Regional Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2011,36(10): 1218-1221. (吴晓莉,平劲松,刘利,等.区域导航系统硬件延迟解算[J]. 武汉大学学报:信息科学版,2011, 36(10):1218-1221.) |
| [20] | BEI Jinzhong, LI Wei, GU Shouzhou. Precise Point Positioning RAIM Method [J]. Acta Geodaetica et Gartographica Sinica, 2011, 40(sup):63-67.(秘金钟,李玮,谷守周.精密单点定位用户自主式完备性监测算法[J]. 测绘学报,2011, 40(sup):63-67.) |
| [21] | ELLIOTT D K,CHRISTOPHER J H. Understanding GPS Principles and Applications[M]. 2nd ed. [S.l.]:Artech House, 2006:224-239. |