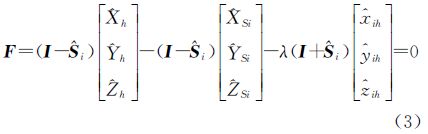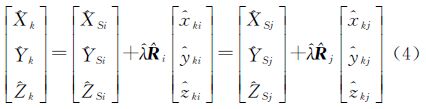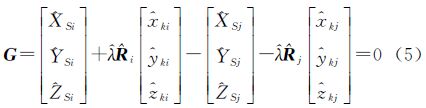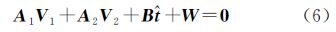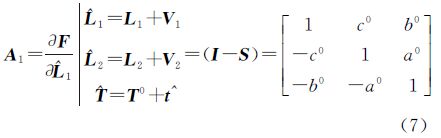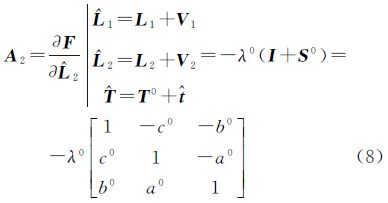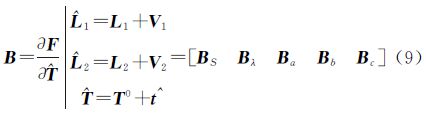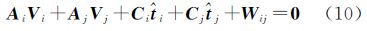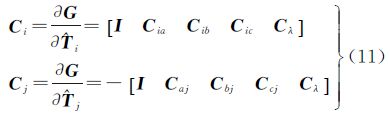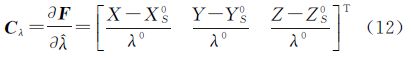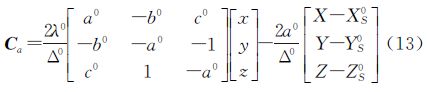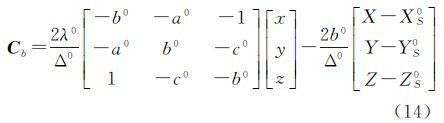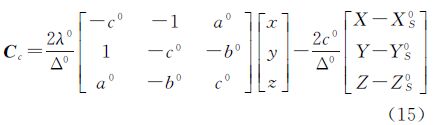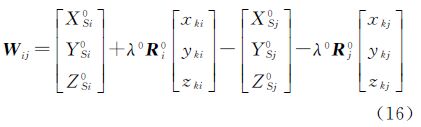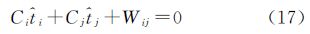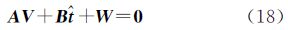1 引 言
地面激光扫描(terrestrial laser scanning，TLS)无论用于闭合的单个物体，还是开放的大范围地形测绘，都需通过有限视场、不同视角、不同空间分辨率的多站扫描，才能完成物体形态或地表形态测量[1]。多站点云坐标的统一通常称为拼接或匹配[2]，点云拼接或匹配是将两块点云调整到一个最适基准的过程，通过两站点云的重叠区域或同名点，按照一定的数学规则进行坐标转换[2, 3]。
目前点云拼接分为5大类：①文献[4]提出的经典ICP算法的点云拼接；②基于反射标靶的(球体标靶、反射片标靶和自然物体标靶等)多站点云拼接[5, 6]；③基于全站仪/GPS控制点多站点云数据的拼接[7]；④基于三维特征点云数据的拼接[1, 3, 8]；⑤空间点投影到某个平面上，将三维匹配转化为二维匹配，如PP和CPP算法[9]。在国内，文献[10, 11]提出了基于影像的点云自动拼接方法。以上拼接方法都是在有较大重叠区域(20%～50%的重叠度)时提取同名点的前提下实现的，要用于开放的、较大范围的地形扫描，则很难实现拼接。基于反射标靶的固定式扫描的单站点云数据本身是三维的，可看成一个独立的三维模型。用3个以上的标靶，可计算单站点云坐标转换参数，然后将点云坐标转换到工程指定的坐标系统。根据文献[12, 13]的有关模型定向理论，此过程称为独立模型法点云定向，该方法对重叠区域无要求，逐站定向即可达到拼接目的。本文在独立模型法点云定向的基础上，提出基于光束法区域网平差的TLS多站点云定向模型，以每个扫描站到定向标靶的射线为单个光束，以每个光束为平差单元，按三维坐标转换模型建立全区域统一的误差方程式，使指向同一个标靶的光束完全相交，整体求解每个扫描站的6(7)个坐标转换参数(6DOF、7DOF)，确定每站点云的定向矩阵，实现多站点云自动定向。光束法区域网平差在摄影测量多个像片定向中的应用已经成熟[14, 15]，文献[16, 17]用标靶进行点云拼接，已体现光束法的基本思想：每站观测设置8个以上标靶，其中4个为连接标靶，解算每站点云坐标转换的13参数。本文对基于光束法区域网平差的多站点云拼接数学模型进行推导，并对平差方法进行分类。以实用性为原则，建议假设指定坐标无误差、扫描坐标是带误差观测值的数学模型作为测绘生产实用模型，其优点是：单个标靶和公共标靶具有相同的方程，即附有未知数的条件方程，平差计算简单实用，具有较高的坐标转换精度。通过实用模型与独立模型法的点云定向比较表明，实用模型的精度有明显提高。
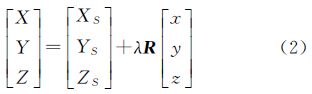
2 点云定向平差模型 2.1 常用拼接模型(三维坐标转换模型)在广泛应用的RISCAN_PRO扫描软件中，利用3个旋转角、3个平移量和缩放因子构成POP矩阵[18]，文献[19]用6参数建立点云拼接数学模型
式中，[x0 y0 z0]T是平移参数，[α β γ]T由roll-pitch-yaw转角系统的3个旋转角构成，其中绕Y轴的旋转角α表示仪器设备x坐标轴与指定坐标系X轴在XZ平面上投影之间的夹角，称为扫描起始方向倾角，即x轴倾角，简称点云滚动角；绕X轴旋转角β表示y轴与指定坐标系Y轴在YZ平面上投影之间的夹角，即y轴倾角，称为旁向倾角；绕Z轴旋转角γ表示x坐标轴与指定坐标系X轴在XY平面上投影之间的夹角，即x轴偏角，简称点云扫描“0”方向偏角；C和S表示余弦函数和正弦函数；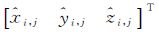
是第i站的第j个扫描点[xi,j yi,j zi,j]T拼接后的坐标。用罗德里格矩阵的3个元素代替3个旋转角，用XS、YS、ZS代表平移参数，建立三维坐标转换模型[20, 21]
式中，平移参数的几何意义为扫描仪中心的三维坐标在指定坐标系的位置，定义为点云定位参数，用XS、YS、ZS表示；R矩阵反映了扫描时的点云在指定坐标系的姿态，从这个意义上讲，将自由点云坐标转换到指定坐标系坐标的过程即为点云的定位和定向(简称点云定向)是合理的。
2.2 光束法区域网平差数学模型
式(1)和式(2)反映了扫描站位置和点云姿态与标靶的指定坐标系坐标和扫描坐标之间的关系。13参数模型[16, 17]的线性化和模型求解过于复杂：式(1)因有三角函数而计算不便，所以选择式(2)为光束法区域网平差的依据。所有光束(所有测站与相关标靶连接起来的路线)构成区域网，全区域方程式有单标靶的附有未知数的条件方程式和公共标靶的附有限制条件的方程两种，且各扫描站有一个共同的缩放参数λ。
根据文献[20, 21]中罗德里格矩阵的性质，i扫描站射向单标靶h的附有未知数平差值方程由式(2)变为
式中，I为三阶单位阵；Ŝi为第i站反对称矩阵的平差值；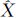
h、
h、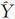
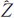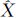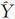h为标靶h的工程测量坐标平差值；Si、Si、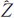Si为第i站扫描站位置坐标；
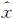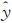ih、
ih、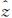
ih为第i站扫描坐标的平差值；λ是缩放参数。
设i站和j站(j≠i)站指向公共标靶k的限制条件方程为
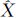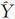式中，k、k、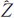k为第i站公共标靶k的工程测量坐标平差值；
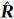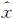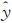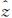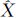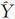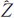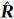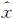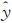i为第i站旋转矩阵平差值；ki、ki、ki为第i站公共标靶k的扫描坐标平差值；Sj、Sj、Sj为第j站的公共标靶的扫描位置坐标；j为第j站的公共标靶的旋转矩阵平差值；kj、kj、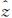kj为第j站公共标靶k的扫描坐标平差值；为缩放参数的平差值。将式(4)写成
假设有N重公共标靶，则可列1个式(3)方程，再列N-1个式(5)方程。
3 区域网平差数学模型解算 3.1 单标靶附有未知数平差值方程线性化为推导公式的方便，省去式(3)的下标i和h，式(3)线性化后矩阵形式为
扫描站定位与定向参数的平差值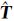
=
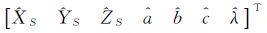，参数近似值T0=[XS0 YS0 ZS0 a0 b0 c0 λ0]T，参数改正数
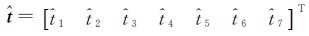，标靶中心在指定坐标系下的坐标L1=[X Y Z]T、扫描坐标系下的坐标L2=[x y z]T，标靶在指定坐标系的坐标改正数V1的系数
式中，A1是函数F对指定坐标系坐标偏导数在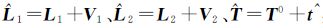
处的导数矩阵。同样标靶扫描坐标系的坐标改正数V2的系数
而定向参数改正数系数
经推导
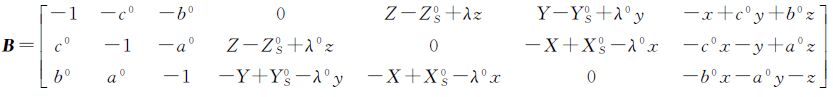
闭合差W=(I-S0)(L1－LS0)－λ0(I+S0)-1L2，其中，LS0=[XS YS ZS]T。
3.2 公共标靶附有限制条件平差值方程的线性化式(5)的线性化形式为
式中，Ai和Aj为i站和j公共标靶坐标改正数的系数Vi和Vj的系数，Ai=λ0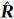i0，Aj=λ0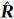j0；
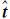i、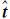j分别为i、j站定向参数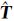i和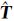j的改正数，其系数
式中，缩放参数的系数
a的改正数系数为
b的改正数系数为
c的改正数系数为
式中各符号含义详见参考文献[21]。
3.3 区域网平差数学模型分类根据参数个数和观测值的不同，单光束单标靶平差值条件方程分为6种，方程代码分别是601、602、603、701、702、703，各方法的系数见表 1。
| 序号 | 平差方法代码 | 参数个数 | 缩放系数 | 假设有误差的坐标 | 观测值改正数系数A | 未知数改正数系数B |
| 1 | 601 | 6 | 1 | X、Y、Z | A1 | [BS Ba Bb Bc] |
| 2 | 602 | 6 | 1 | x、y、z | A2 | [BS Ba Bb Bc] |
| 3 | 603 | 6 | 1 | X、Y、Z x、y、z | [A1 A2] | [BS Ba Bb Bc] |
| 4 | 701 | 7 | λ | X、Y、Z | A1 | [BS Ba Bb Bc Bλ] |
| 5 | 702 | 7 | λ | x、y、z | A2 | [BS Ba Bb Bc Bλ] |
| 6 | 703 | 7 | λ | X、Y、Z x、y、z | [A1 A2] | [BS Ba Bb Bc Bλ] |
公共标靶个数随附有限制条件方程的变化而变化，如假设扫描坐标无误差，则式(10)变为
这样就表示两个扫描站参数之间的关系，因此光束法区域网平差其数学模型共有12种。
3.4 区域网平差的实用模型区域网平差的实用模型选择原则：①模型简单，精度满足工程测量需要；②保证坐标转换后，点云坐标尽量符合新坐标系统中的高精度坐标[25]。按以上原则，优先选择“指定坐标系坐标无误差，扫描坐标系坐标是有误差的观测值”的区域网平差模型，此时标靶指定坐标系下的坐标为常数，单标靶和公共标靶的条件方程变为同一种形式
式中，A为标靶扫描坐标系的坐标改正数V的系数。
3.5 点云定向与摄影测量中的光束法平差的比较点云定向与摄影测量中光束法平差的基本思想一致，都是以数据采集器射向目标的光束为平差单元，建立全区域的平差方程式，统一解算各测站位置和姿态，同时解算加密点或连接点坐标。本文的光束法模型则是已知连接点坐标(用其他方法测量)而不需要解算的特殊情况。其模型主要区别表现为：
(1) 出发公式相似，但意义不同。摄影测量中的光束是摄影机位置、像点和物点3点之间的关系，称为共线方程；前者则是扫描站和定向标靶两点之间的关系，称为坐标转换方程。
(2) 在模型构建上，后者是同名光线相交，构成空中三角形，一个物方点对应2个或2个以上同名像点，然而地面扫描时，受地物遮挡、地物棱角点特征难识别、重叠度不高等因素影响，只靠人工标靶构建区域网。这样的区域网同名光线较少，部分光束是单光束，区域网边缘不能构成封闭多边形，因此点云定向光束法模型有两种，同名光线的平差方程是以各站坐标转换后均等于标靶在指定坐标系中的坐标为约束的，是附有未知数的条件平差方程，而单光束平差方程是坐标转换方程。
(3) 点云定向的光束法一般不考虑解算加密点的功能，因为摄影测量数据只有角度信息，没有距离信息，扫描数据既有角度信息也有距离信息，点云坐标通过转换得到。
(4) 目的比较：摄影测量中光束法的根本目的是解算加密点坐标，而点云定向的根本目的是求解扫描仪扫描的位置和姿态，即求解坐标转换参数，以进行点云坐标转换。
4 试验及分析 4.1 试验数据试验所用扫描仪器为Riegl VZ-1000，共扫描6站，每站布设4～5个自制球形标靶，其中相邻扫描站最少有2个重合标靶，最多有3个重合标靶；每站约4000万个扫描点。用南方GNSS接收机、平滑存储次数为180的RTK方法测量标靶地面点坐标，通过量取标靶中心到地面控制点的高度，将工程指定坐标引入标靶中心[16, 22]。在同一个控制点上，不同时间两次架设的标靶，其目标高不同，但仍然属公共标靶。
工程指定坐标系为1980西安坐标系，以高斯东坐标为X，高斯北坐标为Y，1985国家高程为Z，构成近似的右手三维直角坐标系，以便坐标转换后能直接用于测图。6站共布设15个标靶，其中单独标靶8个，2重标靶2个，3重标靶4个，4重标靶1个，平均每站架设标靶2.5个，每站能扫描4～5个标靶球，共列28组(每组)方程，解算36个定位参数的点云姿态参数。按照式(18)，各扫描站位置和点云姿态参的系数如图 1所示，
表示各站标靶填写的3行6列的系数矩阵，
表示公共标靶补填的3行6列系数矩阵，最后一列的
表示每个标靶的全区域统一缩放系数λ的3行1列系数矩阵(本案例选缩放参数的值为1)。
|
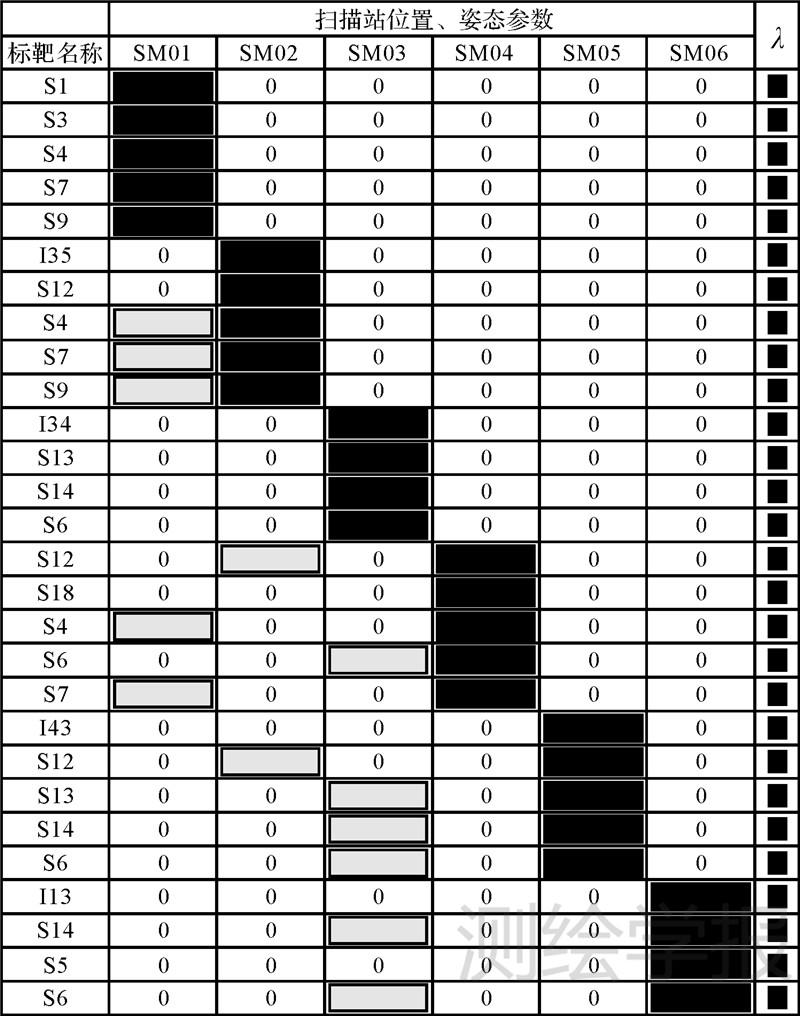
| 图 1 扫描站位置、姿态参数示意图 Fig. 1 Position of scan-station and posture parameters |
数据处理使用IDL语言开发的基于激光点云的EEXLT(地图要素提取)软件的“单站点云独立模型法自动定向”和“区域网平差多站点云自动定向”功能，实现了标靶自动探测、标靶中心坐标拟合[23]、转换参数[24]定向矩阵的自动计算、坐标转换，以及多站点云自动定向。
4.2 数据分析 4.2.1 标靶转换后点位误差分析转换后坐标的精度用3项误差来描述，即平面点位中误差、高程中误差和空间点位中误差。用转换参数和标靶扫描坐标计算的工程指定坐标(计算坐标)与标靶观测的工程指定坐标(观测坐标)之差，计算各站标靶的3项误差。对独立模型法点云定向和区域网平差法定向的3项误差的比较如图 2所示。
|
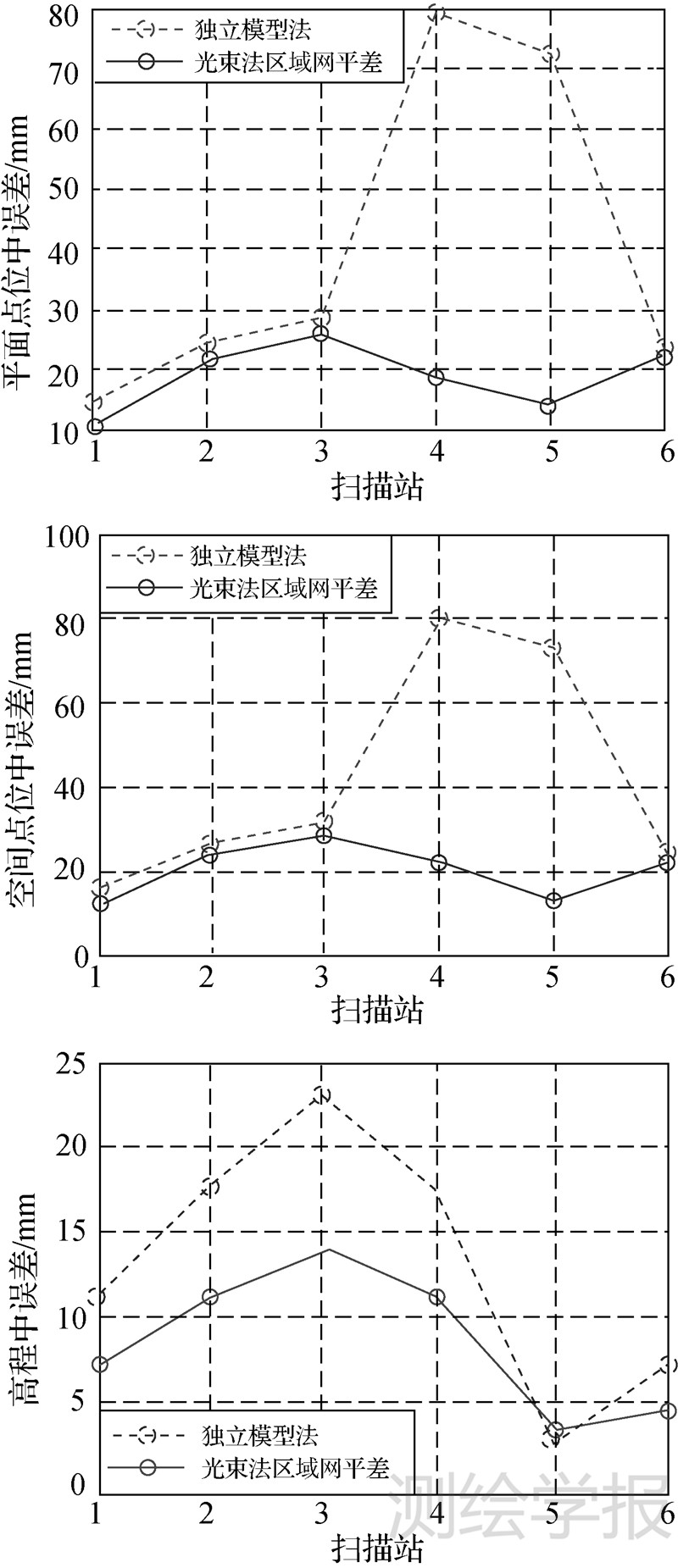
| 图 2 独立模型法和区域网平差标靶点位误差比较 Fig. 2 Comparison of error between IMM and BBA |
图 2表明：①独立模型法3项误差各站有较大差异，而区域网平差法的3项误差变化不大；②区域网平差法平面和空间点位精度高于独立模型法，原因是区域网平差时公共标靶同名光束严格相交；③光束法区域网平差全区域的平面点位误差为19.3 mm、高程误差为14.9 mm、空间点位误差为21.4 mm。
4.2.2 区域网平差多站点云定向的内部精度分析点云定向内符合精度指扫描站内的标靶坐标转换后在统一坐标下的位置中误差；外符合精度指各扫描之间的标靶在坐标转换后在指定坐标中的位置中误差，内部精度统计见表 2。
| 扫描站序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 距离个数 | 10 | 10 | 6 | 10 | 10 | 6 |
| 平面内部符合精度/mm | 15.2 | 32.5 | 40.3 | 23.8 | 19.4 | 25.0 |
根据表 2中数据，52条边之差计算的全区域内部精度为27.3 mm。
4.2.3 区域网平差法与独立模型定向外部精度比较外部符合精度是表达不同扫描站点云转换后标靶中心的相对位置误差，用计算坐标和测量坐标以及两种坐标反算的不同扫描站与标靶间共326条边长计算的区域网平差法定向的外部平面符合精度、高程符合精度、三维符合精度见表 3。
| mm | |||
| 3项外部精度 | 平面外部符合精度 | 高程外部符合精度 | 三维外部符合精度 |
| 独立模型法 | 54.7 | 13.3 | 56.3 |
| 区域网平差法 | 22.3 | 13.0 | 25.9 |
显然光束法精度高于独立模型法。用坐标差计算的全区域平面点位误差(19.3 mm)与外部符合精度相当，因而可以用定向后的点位精度来衡量外部符合精度。
5 结论与展望(1) TLS野外扫描时，平均每站架设2.5个定向标靶球，通过相邻站的公共标靶，使扫描站和标靶构形成的光束构成区域网，可用区域网平差法进行多站点云同时定向，并能减少部分标靶布设的工作量。
(2) 光束法区域网平差能使相邻站指向公共标靶的同名光束严格相交，根据观测值和参数选择不同，平差模型有很多种，本文将罗德里格矩阵的3个独立元素a、b、c作为姿态参数的平差方法分为6种，用实用模型进行试验，外部三维精度达到25.9 mm，比独立模型法的56.3 mm高出1倍多。
(3) 本文试验时标靶指定坐标用南方GNSS接收机采用GNSS RTK方法，以120次平滑存储测定，定位精度为厘米级。当工程建设对测量的精度要求更高时，宜用高精度全站仪和精密水准仪测量。
(4) 用光束法区域网平差进行多站点云定向，转换后的坐标能满足1∶500地形图测量的需要，要用于精密工程测量，还需作进一步研究。
| [1] | LI N, CHENG P, SUTTON M A,et al. Three-dimensional Point Cloud Registration by Matching Surface Features with Relaxation Labeling Method[J].Society for Experimental Mechanics,2005,45(1):71-82. |
| [2] | SEEGER S, LABOUREUX X. Feature Extraction and Registration: An Overview[J]. Principles of 3D Image Analysis and Synthesis, 2002(5): 153-166. |
| [3] | DRUON S, ALDON M J, CROSNIER A. Color Constrained ICP for Registration of Large Unstructured 3D Color Data Sets[C]//Information Acquisition, 2006 IEEE International Conference on. [S.l.]:IEEE, 2006: 249-255. |
| [4] | BESL P J, MCKAY N D. A Method for Registration of 3-D Shapes[J]. IEEE Transaction Pattern Annual Machine Intelligence,1992, 14:239-256. |
| [5] | SHAHAR B, SAGI F. Keypoint Based Autonomous Registration of Terrestrial Laser Point-clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008,63:19-35. |
| [6] | BORNAZ L, LINGUA A, RINAUDO F. A New Software for the Automatic Registration of 3D Digital Models Acquired Using Laser Scanner Devices[C]//CIPA WG 6 International Workshop Scanning for Cultural Heritage Recording. Corfu:[s.n.],2002: 1-2. |
| [7] | ALEXANDER C, TANSEY K, KADUK J, et al. Backscatter Coefficient as an Attribute for the Classification of Full-waveform Airborne Laser Scanning Data in Urban Areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(5): 423-432. |
| [8] | LI X, IGOR G, JACOB B. Robust Alignment of Multi-view Range Data to CAD Model[C]// Proceedings of the IEEE International Conference on Shape Modeling and Applications. Washington: IEEE, 2006. |
| [9] | SOONYONG Park. A Fast Point-to-Tangent Plane Technique for Multi-view Registration[C]//Proceedings of Fourth International Conference on Digital Object Identifier. Philadelphia:[s.n.],2003: 276-283. |
| [10] | ZHAI Ruifang,ZHANG Jianqing. Automatic Registration of Point Clouds Based on Laser Scanner[J].Geospatial Information,2004,2(6):37-39. (翟瑞芳,张剑清.基于激光扫描仪的点云模型的自动拼接[J].地理空间信息,2004,2(6):37-39.) |
| [11] | ZHANG Jianqing,ZHAI Ruifang,ZHENG Shunyi.Automatic Seamless Registration of 3D Multiple Range Views[J].Geomatics and Information Science of Wuhan University,2007,32(2):100-103. ( 张剑清,翟瑞芳,郑顺义.激光扫描多三维视图的全自动无缝镶嵌[J].武汉大学学报:信息科学版, 2007,32(2):100-103.) |
| [12] | SHAHAR B A,SAGI F. Keypoint Based Autonomous Registration of Terrestrial Laser Point-clouds[J].ISPRS Journal of Photogrammetry & Remote Sensing, 2008,63:19-35. |
| [13] | LI Deren,ZHENG Zhaobao. Analytical Photogrammetry[M]Beijing:Surveying and Mapping Press, 1992:161-165. (李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992:161-165.) |
| [14] | LI Deren, ZHAO Shuangming, LU Yuhong, et al. Combined Block Adjustment for Airborne Three line CCD Scanner Images[J]. Acta Geodaetica et Cartographica Sinica,2007, 36(3):245-250.(李德仁, 赵双明, 陆宇红,等. 机载三线阵传感器影像区域网联合平差[J].测绘学报,2007, 36(3):245-250.) |
| [15] | YUAN Xiuxiao. POS-supported Bundle Block Adjustment[J].Acta Geodaetica et Cartographica Sinica,2008,37(3):342-348.(袁修孝. POS辅助光束法区域网平差[J].测绘学报, 2008,37(3):342-348.) |
| [16] | ZHAO Xu. 3D Reconstruction Method for Large Scale Relic Landscape from Laser Point Cloud[J]. Geomatics and Information Science of Wuhan University,2008,33(7):684-687.(赵煦. 基于激光点云的大型文物景观三维重建方法[J]. 武汉大学学报:信息科学版, 2008,33(7):684-687.) |
| [17] | YANG Wei. Analysis Accuracy of 3D Coordinate Transformation for Laser Scanning Data[J]. Geotechnical Investigation and Surveying, 2004(3):61-63. (杨伟.激光扫描数据三维坐标转换的精度分析[J].工程勘察, 2004(3):61-63.) |
| [18] | RIEGL. RiSCAN PRO[EB/OL].[2014-02-06]. http://www.riegl.com/index.php?id=221. |
| [19] | ANTHONY M, JORGE L,MARTíNEZ,et al. Fast Range-independent Spherical Subsampling of 3D Laser Scanner Points and Data Reduction Performance Evaluation for Scene Registration[J]. Pattern Recognition Letters, 2010,31: 1239-1250. |
| [20] | YAO Jili. Rigorous Formula for Direct Calculating Parameter in 3D Transformation[J]. Bulletin of Surveying and Mapping, 2006(5):7-9.(姚吉利. 3维坐标转换参数直接计算的严密公式[J]. 测绘通报, 2006(5):7-9.) |
| [21] | YAO Jili, HAN Baomin, YANG Yuanxi. Applications of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12):1094-1096.(姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报:信息科学版, 2006, 31(12):1094-1096.) |
| [22] | LUO Dean.Whole Object Deformation Monitoring Based on 3D Laser Scanning Technology[J]. Bulletin of Surveying and mapping, 2005(7):40-42. (罗德安.基于3维激光影像扫描技术的整体变形监测[J]. 测绘通报,2005(7):40-42.) |
| [23] | YAO Jili. Method for Metal Mine Surveying Based on 3D Laser Scanning Technique[J]. Metal Mine,2011(7):114-117.(姚吉利.基于3D激光扫描的金属矿测量方法研究[J].金属矿山,2011(7):114-117.) |
| [24] | YAO Jili. SARC Model of Three-Dimensional Coordinate Transformation [J]. Geomatics and Information Science of Wuhan University, 2005, 30(9):825-828.(姚吉利. 三维坐标转换的静态滤波模型[J]. 武汉大学学报:信息科学版,2005, 30(9):825-828.) |
| [25] | YANG Yuanxi,XU Tianhe. The Combined Method of Datum Transformation between Different Coordinate Systems[J]. Geomatics and Informatic Science of Wuhan University. 2001, 26(6):509-512.(杨元喜,徐天河.不同坐标系综合变换法[J]. 武汉大学学报:信息科学版, 2001, 26(6):509-512.) |
| [26] | Subject Group of Survey Adjustment, School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment [M]. Wuhan:Wuhan University Press, 2003. (武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社, 2003.) |