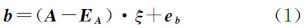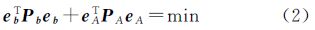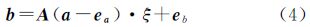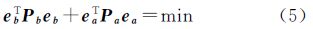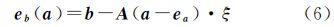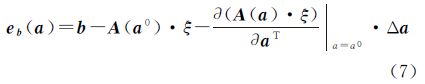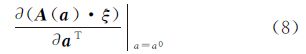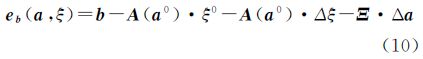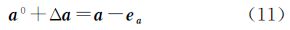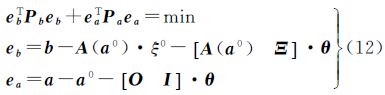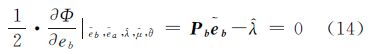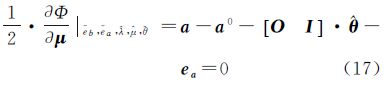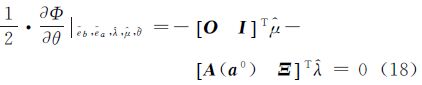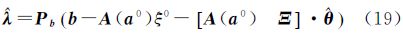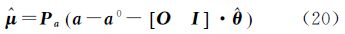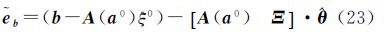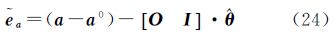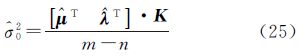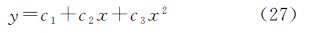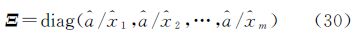2. 现代工程测量国家测绘地理信息局重点实验室,上海 200092
2. Key Laboratory of Modern Engineering Surveying of National Administration of Surveying,Mapping and Geoinformation,Shanghai 200092,China
1 引 言
整体最小二乘法(total least squares,TLS)的起源可以追溯到19世纪70年代[1],这种方法最初在统计领域开始流行,称为误差变量模型(error in variable,EIV)。 文献[2]在20世纪80年代初提出“total least squares”这一术语[2],实质是从数字分析角度对线性EIV模型重新进行定义。至此以后,TLS法迎来了快速发展期,广泛地应用于系统识别领域[3]、信号处理领域[4]、天文学领域[5]等。TLS平差法是最小二乘(least squares,LS)平差方法的一种自然扩展,在LS基础上考虑系数矩阵受误差干扰的情况,使平差理论更严密,因而越来越受到测绘领域的重视。但是,TLS法引入大地测量数据处理领域的时间相对较晚,1999 年文献[6]应用其进行曲线拟合。随后,文献[7]将TLS法引入GPS数据处理中以提高GPS的定位精度。2005年,文献[8]应用TLS法进行地理统计分析,指出该方法优于加权LS法。文献[9] 将TLS法应用于变形分析中,但其实质是用TLS法进行坐标变换。目前,TLS法(包含其扩展模型)的应用主要集中在坐标变换方面[10, 11, 12, 13, 14, 15, 16, 17, 18]。TLS平差法还频繁地出现在直线拟合[19]和线性回归分析[20]参数估计中。
根据测绘学科自身的特点,TLS平差模型本身也在不断扩展。考虑到估计参数之间满足某种函数关系,文献[21, 22, 23]提出约束TLS平差法;考虑到观测向量为多维情况,文献[11, 12]提出多维TLS平差法;考虑到观测向量和系数矩阵间异方差情况,文献[20]提出了加权TLS平差方法;针对文献[20]的解算方法相对复杂的情况,文献[24]提出了一种简化的加权TLS平差迭代算法。在坐标变换中系数矩阵可能含有重复变量,即结构TLS问题,除采用结构TLS法外也可以通过加权的方式处理[16]。文献[25]对含有随机参数的情况进行了详细讨论,并给出加权TLS解存在的必要条件。国内对TLS平差方法的研究也比较多,主要集中在三维坐标变换参数估计[26, 27, 28, 29, 30, 31]、三维激光扫描数据处理[28, 32]、应变参数反演[33]、自回归参数估计[34],对TLS平差算法也进行了一些研究[35, 36, 37]。在模型方面,文献[38]提出了稳健TLS平差法;文献[39]研究了广义正则化的TLS平差问题。
然而,上述研究都是在线性函数模型条件下进行的讨论,即系数矩阵的每个元素都是自变量(包括常数)。但是在测量平差中经常出现非线性的情况,例如非线性回归。此时,系数矩阵中的各元素不再是自变量,而是关于自变量的函数,即各元素为函数表达式。因此,有必要对非线性TLS问题进行讨论。尽管非线性EIV模型已经不是一个新问题,但是从测量平差和数据分析角度对非线性整体最小二乘问题(nonlinear total least squares,NTLS)进行讨论并不多见。本文采用拉格朗日极值条件式推导基于牛顿型解法的NTLS平差迭代算法,最后通过非线性回归和曲线拟合算例验证该方法在等精度和非等精度情况下的可行性和有效性。
2 非线性整体最小平差模型经典整体最小二乘法的观测方程可以描述为
式中,b∈Rm×1是观测向量;eb∈Rm×1是与观测向量相对应的误差向量;A∈Rm×n是含有误差的系数矩阵;EA∈Rm×n是系数矩阵相对应的误差矩阵;ξ∈Rn×1是参数向量。尽管在解算TLS问题时其可认为是一非线性问题,但是从系数矩阵元素的结构和类型角度分析其应该是一线性模型,因为系数矩阵中的各元素都是自变量。经典TLS法的平差准则是
式中,Pb∈Rm×m和PA∈Rmn×mn分别是观测向量和系数矩阵元素组成的列向量的权矩阵,在经典TLS平差中它们都是单位矩阵;eA∈Rmn×1=vec(EA),vec(·)表示矩阵的拉直计算,它是将矩阵按列重新排列成一新的列向量。对于经典TLS问题的解算方法,最常用的是SVD分解法,但是当系数矩阵元素之间存在相关性时,SVD分解就不能获得最或然估计结果[40]。如果上述权矩阵不是单位矩阵,最为常用的解算方法便是基于牛顿型的迭代算法[20]。值得注意的是,对于按行独立的加权TLS法与附加参数的条件平差法获得的估计结果具有等价性[41]。
如果系数矩阵元素不再是独立的自变量,而是关于某一自变向量a的函数,此时系数矩阵不再是线性关系,例如
此时,系数矩阵A的元素不再是自变量x本身而是关于变量的函数,即系数矩阵的各元素可以由自变矢量a计算得到。将这种TLS平差问题称为非线性整体平差(NTLS)。
根据经典TLS法的描述,NTLS平差的观测方程可以表达为
式中,a∈Rq×1是系数矩阵A的输入向量,该向量元素之间可以是相互独立的自变量也可以是相关量;ea∈Rq×1是输入向量a对应的误差向量。非线性TLS极小条件可以描述为
式中,Pa∈Rq×q是输入向量的权矩阵。
3 解非线性整体平差问题NTLS问题可以看成是一个双非线性问题。为能够解算NTLS问题,将式(4)表达成观测误差eb关于a的函数,即
将上式在a0处展开并整理,得
此时
是一个大小为m×q,关于ξ的非线性矩阵,需进一步进行线性化,将式(7)在ξ0处展开
略去二次极小项乘积整理后,得
在上述的公式推导过程中,隐含有如下的等式条件
以及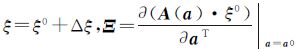 。
。
现在,NTLS就变成在极值条件(5)和方程(10)以及方程(11)的共同条件下求取参数的最佳估值以及观测向量和输入向量的最佳近似值的问题。即
式中,θ=[Δξ Δa]T;O和I分别是(m×n)的零矩阵和(q×q)的单位矩阵。
利用拉格朗日极值条件对方程组(12)构建如下的目标函数
对式(13)中各元素分别求导整理后,得
式中,“~”表示最佳近似值;“ ^ ”表示最佳估计值。将式(14)和式(15)分别代入式(16)和式(17)中整理后,有
将求得的拉格朗日参数和代入式(18)中可以求得
式中
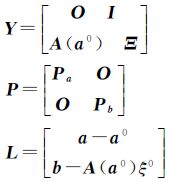
对式(21)的左边求逆后,可以得到
式中,N=YTPY。
获得最佳参数估计以后,联合式(19)和式(20)以及式(14)和式(15)可以解得误差量的最佳近似值计算公式
因此,可以得到方差分量的估计公式
式中
4 计算流程根据上一节的推导,将NTLS平差的算法流程设计如下。
输入数据:观测向量b,系数矩阵输入向量a、权矩阵Pb和Pa以及迭代终止条件ε(本文各次计算均设置其等于1e-8)。
第1步,令a(0)=a,仅考虑观测向量b的误差,采用LS平差法求得参数ξ的初始估计值ξ(0),并计算
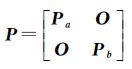
第2步,采用前一步获得的初始参数值和已知值分别计算
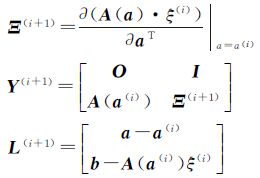
然后代入公式
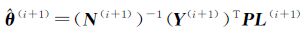
中计算参数θ的估计值,并将该估计值分解成Δξ(i+1)和Δa(i+1)两部分,并用公式ξ(i+1)=ξ(i)+Δξ(i+1)和a(i+1)=a(i)+Δa(i+1)计算新的最佳估计量。
第3步,重复第2步直到Δξ(i+1)和Δa(i+1)的2范数都小于指定的收敛条件ε,并根据式(25)计算验后方差估计值。
输出数据: 、a以及验后方差估计值
、a以及验后方差估计值 02。
02。
本文所讨论的NTLS问题经常出现在非线性回归分析中。多种模型可以通过取对数的方式线性化,然后得到各种新的观测方程。其中,二次曲线回归模型是最为常见的一种非线性回归分析模型。同时,在非线性回归分析当中,各观测量通常都是在相同条件下的观测值,即等权。因此,首先考虑二次曲线回归模型,用其来验证本文给出算法的可行性。
二次曲线回归模型通常可以表达为
式中,x和y都是含有误差的观测值;c1、c2、c3是回归系数。
假设在某处通过测量获得如表 1所示的20组观测数据,x和y坐标是等精度观测,中误差为0.05 m。
| 点号 | x | y | 点号 | x | y |
| 1 | 1.004 | 7.104 | 11 | 10.991 | 201.351 |
| 2 | 1.992 | 13.956 | 12 | 12.004 | 236.132 |
| 3 | 3.008 | 23.635 | 13 | 12.990 | 273.705 |
| 4 | 3.988 | 36.069 | 14 | 13.997 | 314.093 |
| 5 | 5.003 | 51.288 | 15 | 15.021 | 357.235 |
| 6 | 5.983 | 69.315 | 16 | 15.985 | 403.173 |
| 7 | 7.004 | 90.157 | 17 | 16.998 | 451.942 |
| 8 | 7.990 | 113.757 | 18 | 17.989 | 503.465 |
| 9 | 8.979 | 140.160 | 19 | 19.017 | 557.778 |
| 10 | 9.999 | 169.372 | 20 | 20.013 | 614.910 |
根据前面的讨论知道,在采用本文给出的NTLS平差迭代算法的过程中,在获得初始参数估计值以后,需要计算Ξ矩阵。在本次的回归系数估计中,该矩阵结构为
分别采用LS平差法和NTLS平差法对表 1中的观测数据进行回归系数估计,将估计得到的参数结果列于表 2中。
| LS | 绝对差 | NTLS | 绝对差 | 真值 | |
| c1 | 2.814 2 | -0.208 8 | 2.946 1 | -0.076 9 | 3.023 |
| c2 | 2.775 6 | 0.101 6 | 2.734 1 | 0.060 1 | 2.674 |
| c3 | 1.390 3 | -0.005 7 | 1.392 4 | -0.003 6 | 1.396 |
需要注意的是,在采用LS平差法的过程中,因为认为系数矩阵元素不含有任何误差,故直接采用x的值和元素表达式计算得到的结果作为系数据矩阵元素值。
从表 2获得的结果可以发现,NTLS法获得的估计值与真值之间的差值比LS平差法获得的估计值与真值之间的差值小很多,特别是截断参数的估计。这说明,本文给出的算法能够获得比LS平差法更好的估计结果。
上面的试验是在单独一次估计中获得的结果,为进一步说明NTLS法比LS法优越,将上面的试验进行改进,设计如下:
回归系数的真值仍然采用表 2中描述的值,对真值坐标附加上从0.001 m开始,步长为0.003 m,到0.1 m结束的中误差,在每个中误差情况下模拟500次。不同中误差情况下获得的参数估计值的平均值与真值之差同先验中误差值的关系如图 1所示。

|
| 图 1 参数估计值与真实值的差值 Fig. 1 Difference of the parameters between the estimated values and the true ones |
从图中可以看出,当误差比较小时,LS平差法和NTLS平差法获得的参数估计结果非常接近。在本例中,当中误差小于0.013 m时,它们的估计结果几乎完全相同。同时发现高次项对应的系数,不管在什么误差情况下两种方法都能够获得几乎与真值完成相同的结果。随着误差的增加以及幂的降低,系数的估计结果与真值的差距越来越大,但是NTLS方法获得的结果总比LS法获得的结果更接近于真实值。
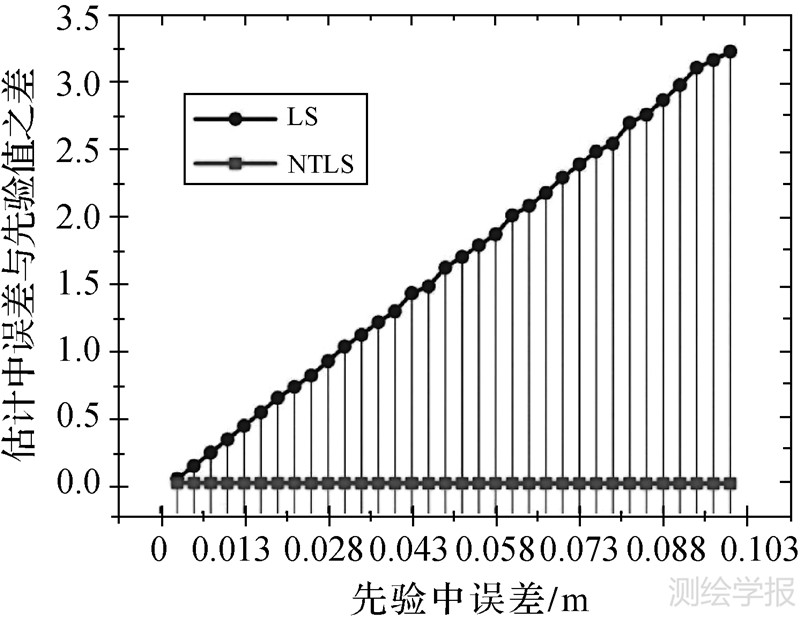
将模拟500次后获得的验后中误差平均值与先验的中误差值的差值随误差增长的变化关系描述在图 2中。
|
| 图 2 估计中误差与先验值的差值 Fig. 2 Difference of the MSE between the prior value and the estimated ones |
从图 2的描述来看,LS平差法很难获得正确的验后中误差估计,相反,NTLS平差法能获得与先验值几乎一致的估计结果。因为从图上看,其估计结果与先验值的差一直都在零附近波动。这些都说明,在等权情况下,NTLS平差法处理系数矩阵非线性情况下的平差问题时比LS平差法更好。
5.2 非等权情况(以对数函数曲线为例)前面对等权情况下的NTLS平差法进行了试验讨论,然而在测量数据处理中,非等精度观测的情况经常出现,有必要对非等权情况下的NTLS平差问题进行讨论。假设有如下的对数曲线模型
式中,a和b是待估计系数;x和y都是观测量。假设它们的观测精度分别为0.08 m和0.02 m。同样分别采用NTLS平差法和LS平差法进行估计。在NTLS平差的过程中,Ξ矩阵的结构应该为
两种方法都模拟500次,将获得的参数平均值以及平均值与设计真值的差值列于表 3。
| 参数 | LS平差法 | NTLS平差法 | 真值 | |||
| 估计值 | 绝对差 | 估计值 | 绝对差 | |||
| â | 2.341 91 | 0.001 91 | 2.340 98 | 0.000 98 | 2.34 | |
 | 3.099 38 | -0.000 62 | 3.099 68 | -0.000 32 | 3.10 | |
从表 3不难发现,NTLS平差法获得的参数估计值比LS平差法获得的估计值更接近于真值,这说明NTLS平差法比LS平差法在参数估计部分更有效。尽管在此取得平均值,但在试验过程中发现它同等权情况时一样,每个点的估计值都比LS平差法更接近真实值,因此,避免重复,此处就没有再将其列出。
在定权的过程中,先验单位权方差取为1 m2。LS平差法采用
计算验后单位权方差,而TNLS平差法采用式(25)计算。将模拟500次获得的单位权方差估计值作为y轴,模拟次数作为x轴绘制成图 3。

|
| 图 3 两种方法的估计单位权方差 Fig. 3 Estimated variance components of the classical LS and the NTLS algorithm |
图 3中的横线表示两种方法获得的单位权方差估计平均值。此图说明,NTLS平差获得单位权方差估计值与输入的先验单位权方差值几乎完全一致;而LS平差获得的单位权方差估计值出现较大偏差,这主要是因为其没有考虑系数矩阵中的误差。这说明本文给出的算法是有效并合理的。
6 结 论本文对NTLS问题进行了研究,并给出了一种迭代计算方法。可以得出以下几点结论:
(1) NTLS方法保证了系数矩阵中不同位置的非线性元素的同一自变量获得相同的误差改正,常数元素项不获得任何改正值,其平差理论相对严密。
(2) 本文给出的算法,对于初始值的要求相对较低,不需要非线性LS法来获取初始值,直接采用线性最小二乘结果即可。
(3) 不管是等权或是非等权情况,NTLS法获得参数估计结果都更接近真实值,方差估计结果也更接近先验值。
文章仅就一种算法进行了讨论,而对于NTLS问题的其他方面没有涉及,例如模型在测绘科学技术中更广泛的应用等,这是笔者需要进一步努力研究的方向。
| [1] | ADCOCK R J. Note on the Method of Least Squares[J]. The Analyst, 1877, 4(6):183-184. |
| [2] | GOLUB G H , VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980,17(6): 883-893. |
| [3] | GUILLAUME P, PINTELON R, SCHOUKENS J. A Weighted Total Least Squares Estimator for Multivariable Systems with Nearly Maximum Likelihood Properties[J].IEEE Transactions on Instrumentation and Measurement, 1998,47(4): 818-822. |
| [4] | DOWLING E M, DEGROAT R D, LINEBARGER D A. Total Least Squares with Linear Constraints[C]//Proceeding on ICASSP-92. San Francisco: IEEE, 1992: 341-344. |
| [5] | BRANHAM R L. A Covariance Matrix for Total Least Squares with Heteroscedastic Data[J].The Astronomical Journal, 1999,117:1942-1948. |
| [6] | DAVIS T G. Total Least-Squares Spiral Curve Fitting[J]. Journal of Surveying Engineering, 1999,125(4):159-176. |
| [7] | LIU L, TIAN Z, HUANG S. Using TLS Algorithm to Improve GPS Positioning Precision with Altitude Hold Mode[J]. Journal of Electronics , 2002,19(2):120-124. |
| [8] | FELUS Y A , SCHAFFRIN B. A Total Least-Squares Approach in Two Stages for Semivariogram Modeling of Aeromagnetic Data[J]. GIS and Spatial Analysis, 2005(1): 215-220. |
| [9] | ACAR M, ZLVDEMIR M T, AKYILMAZ O. Deformation Analysis with Total Least Squares[J]. Natural Hazards and Earth System Sciences, 2006, 6(4): 663-669. |
| [10] | AKYILMAZ O.Total Least Squares Solution of Coordinate Transformation[J]. Survey Review, 2007, 39(303): 68-80. |
| [11] | SCHAFFRIN B, FELUS Y A. Multivariate Total Least-Squares Adjustment for Empirical Affine Transformations[C]//Proceedings of the VI Hotine-Marussi Symposium of Theoretical and Computational Geodesy: Challenge and Role of Modern Geodesy. Wuhan:IEEE,2008:238-242. |
| [12] | SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-Squares Approach to Empirical Coordinate Transfor- mations:Three Algorithms[J].Journal of Geodesy,2008,82(6):373-383. |
| [13] | FELUS Y A, BURTCH R C. On Symmetrical Three-dimensional Datum Conversion[J]. GPS Solutions, 2009,13(1): 65-74. |
| [14] | SCHAFFRIN B, WIESER A. Empirical Affine Reference Frame Transformations by Weighted Multivariate TLS Adjustment[J]. Geodetic Reference Frames, 2009,13(4): 213-218. |
| [15] | NEITZEL F. Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010,84(12): 751-762. |
| [16] | MAHBOUB V. On Weighted Total Least-Squares for Geodetic Transformations[J]. Journal of Geodesy, 2011,86(6): 1-9. |
| [17] | ZHOU Y, DENG C, ZHU J. Weighted Total Least Squares for Rigid Body Transformation and Comparative Study on Heteroscedastic Points[C]// International Symposium on Lidar and Radar Mapping Technologies.Nanjing:SPIE, 2011. |
| [18] | MAHBOUB V. On Weighted Total Least-Squares for Geodetic Transformations[J]. Journal of Geodesy, 2012,86(5): 359-367. |
| [19] | KRYSTEK M, ANTON M. A Weighted Total Least-Squares Algorithm for Fitting a Straight Line[J]. Measurement Science and Technology, 2007, 18(11):3438-3442. |
| [20] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [21] | SCHAFFRIN B, FELUS Y A. On Total Least-Squares Adjustment with Constraints[C]//A Window on the Future of Geodesy. Berlin Heidelberg:Springer, 2005: 417-421. |
| [22] | SCHAFFRIN B.A Note on Constrained Total Least-Squares Estimation[J]. Linear Algebra and Its Applications,2006, 417(1):245-258. |
| [23] | SCHAFFRIN B, FELUS Y A. An Algorithmic Approach to the Total Least-Squares Problem with Linear And Quadratic Constraints[J]. Studia Geophysica and Geodaetica, 2009, 53(1): 1-16. |
| [24] | SHEN Y Z, LI B F,CHEN Y. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy, 2011,85(4): 229-238. |
| [25] | FANG X. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [26] | GE Xuming,WU Jicang. Iterative Method of Weight Constraint Total Least-Squares for Three-Dimensional Datum Transformation[J]. Geomatics and Information Science of Wuhan University, 2012,37(2):178-182.(葛旭明,伍吉仓.三维基准转换的约束加权混合整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版, 2012,37(2): 178-182.) |
| [27] | LU Jue,CHEN Yi,ZHENG Bo. Applying Total Least Squares to Three-dimensional Datum Transformation [J]. Journal of Geodesy and Geodynamics,2008,28(5):77-81.(陆珏, 陈义,郑波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2008,28(5):77-81.) |
| [28] | CHEN Weixian, CHEN Yi, YUAN Qing,et al. Application of Weighted Total Least-Squares to Target Fitting of Three-Dimensional Laser Scanning[J]. Journal of Geodesy and Geodynamics,2010,30(5):90-96.(陈玮娴, 陈义,袁庆, 等.加权总体最小二乘在三维激光标靶拟合中的应用[J].大地测量与地球动力学, 2010,30(5): 90-96.) |
| [29] | LU Jue,CHEN Yi,ZHENG Bo. Application of Weighted Total Least Squares in ITRF Transformation[J]. Journal of Geodesy and Geodynamics,2011,31(4):84-89.(陆珏, 陈义,郑波.加权总体最小二乘方法在ITRF转换中的应用[J].大地测量与地球动力学, 2011,30(04): 84-89.) |
| [30] | YUAN Qing,LOU Lizhi,CHEN Weixian. The Application of the Weighted Total Least-squares to Three Dimensional Datum Transformation[J]. Acta Geodaetica et Cartographica Sinica,2011,40(S1):115-119.(袁庆, 楼立志,陈玮娴.加权整体最小二乘在三维基准转换中的应用[J].测绘学报, 2011,40(S1):115-119.) |
| [31] | ZHOU Yongjun,DENG Caihua. Weighted and Unweighted Total Least Square Methods and Applications to Heteroscedastic 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University,2012,37(8): 976-979,1007.(周拥军,邓才华.加权和不加权TLS方法及其在不等精度坐标变换中的应用[J]. 武汉大学学报:信息科学版, 2012,37(8):976-979,1007.) |
| [32] | CHEN Weixian, YUAN Qing ,CHEN Yi. Application of Constrained Total Least-Squares to Cloud Point Registration[J]. Journal of Geodesy and Geodynamics,2011,31(2):137-141.(陈玮娴,袁庆,陈义.约束整体最小二乘在点云拼接中的应用[J]. 大地测量与地球动力学, 2011,31(2):137-141.) |
| [33] | WANG Leyang, XU Caijun, LU Tieding. Inversion of Strain Parameter Using Distance Changes Based on Total Least Squares[J].Geomatics and Information Science of Wuhan University,2010,35(2):181-184.(王乐洋, 许才军,鲁铁定.边长变化反演应变参数的整体最小二乘方法[J]. 武汉大学学报:信息科学版, 2010,31(2):181-184.) |
| [34] | HU Chuan,CHEN Yi.Parameters Estimation of Autoregression with Structured Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2013,33(1): 45-47(胡川,陈义.自回归模型参数的结构整体最小二乘估计[J].大地测量与地球动力学, 2013,33(1): 45-47.) |
| [35] | LU Tieding, ZHOU Shijian. An Iterative Algorithm for Total Least Squares Estimation[J].Geomatics and Information Science of Wuhan University, 2010,35(11): 1351-1354.(鲁铁定 ,周世健.整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版, 2010,35(11): 1351-1354.) |
| [36] | WANG Leyang, XU Caijun.Iterative Method of Weight Constraint Total Least-Squares for Three-Dimensional Datum Transformation[J].Geomatics and Information Science of Wuhan University, 2011,36(8): 887-890.(王乐洋,许才军.附有相对权比的整体最小二乘平差[J]. 武汉大学学报:信息科学版, 2011,36(8): 887-890.) |
| [37] | HU Chuan,CHEN Yi. An Innovated Algorithm for Solution of Weighted Total Least Squares Adjustments[J]. Journal of Geodesy and Geodynamics, 2012,32(6):106-110.(胡川,陈义.解加权整体最小二乘平差问题的一种新方法[J].大地测量与地球动力学,2012,32(6):106-110.) |
| [38] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares [J]. Acta Geodaetica et Cartographica Sinica,2012,41 (5) :715-722. (陈义,陆珏.以三维坐标转换为例解算稳健总体最小二乘方法 [J]. 测绘学报, 2012,41 (5) :715-722.) |
| [39] | GE Xuming,WU Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3): 372-377.(葛旭明,伍吉仓. 病态整体最小二乘问题的广义正则化[J].测绘学报, 2012,41(3): 372-377.) |
| [40] | VAN HUFFEL S, PARK H, ROSEN J B. Formulation and Solution of Structured Total Least Norm Problems for Parameter Estimation[J]. IEEE Transactions on Signal Processing,1996, 44(10): 2464-2474. |
| [41] | ZHOU Yongjun,ZHU Jianjun,DENG Caihua. The Consistency between Row-wised Weighted Total Least Squares and Condition Adjustment with Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(1):48-53,58.(周拥军, 朱建军, 邓才华.附参数的条件平差与按行独立的加权整体最小二乘法估计的一致性研究[J]. 测绘学报, 2012,41(1):48-53,58.) |