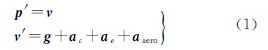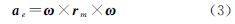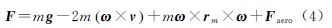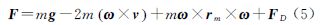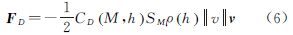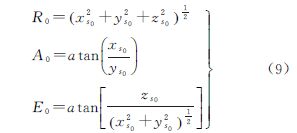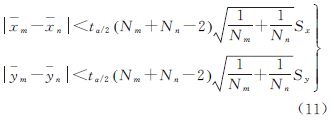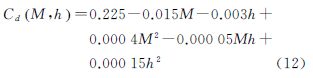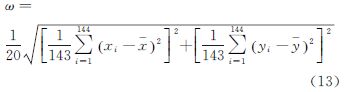2. 海军工程大学 导航工程系，湖北 武汉430033；
3. 91550部队，辽宁 大连116023；
4. 国家海洋局 海底科学重点实验室,浙江 杭州 310012
2. Department of Navigation,Naval University of Engineering,Wuhan 430033,China;
3. Troops 91550,Dalian 116023,China;
4. Key Lab of Submarine Geosciences,State Oceanic Administration,the People’s Republic of China,Hangzhou 310012,China
1 引 言
飞行器被动段运行轨迹解算是根据在轨飞行器当前所处位置、速度、形状和姿态等信息，确定其到达地球或其他星体表面前各时刻坐标位置及其他参数的数据处理技术[1]，其目的主要体现在以下4个方面：①航程安全性评估；②飞行器到达地面时刻预警；③飞行器拦截；④再入体搜索范围确定[2, 3]。飞行器运行轨迹解算涉及计算机仿真、空气动力学、数理统计、测量技术等多学科领域[4]，影响其计算精度的因素主要有飞行器位置观测误差、数据处理误差等。随着观测仪器精度的不断提升，目前飞行器位置和速度观测误差均可控制在亚米级，因此仪器观测误差对落点预报的影响在一定条件下可以忽略不计。此时，数据处理模型的优劣直接决定了运行轨迹的计算精度[5]。
运行在高空(高度大于90km)的无控制、常质量飞行器在无动力状况下的运行区间称为被动段，该阶段又可分为自由飞行段和再入段，这两个阶段受力状况不同，其数学处理模型也有所差异[6, 7]。在早期实时数据处理中，采用的数学模型通常是抛物线模型和椭圆模型等，这两种模型计算方法简单、速度较快，能大致计算出飞行器的运行轨迹。但因未考虑到空气阻力、科氏力以及离心力等因素的影响，且对引力加速度数值计算较为粗略，其计算结果精度较低。现阶段，飞行器运行轨迹模型考虑了上述因素的影响，采用数值积分法求解飞行器被动段运动方程初值问题，提升了计算结果精度，但仍存在一些不足之处，如对空气阻力影响考虑不够充分，通常将空气阻力系数设为常数[8]；同时，引力场模型一般仅取到2阶项，该做法是否合理以及精度如何还有待于进一步评估[9, 10]。为了精确确定飞行器落点位置，通常需要根据不同时刻的飞行器状态观测值分别计算落点位置，再结合统计分析、操作人员经验得到落点位置唯一值，这种做法受人为因素制约较大，具有一定偶然性。本文在空间直角坐标系中建立了高空飞行器被动段运行轨迹数学模型，引用了精度更高的全球引力场球谐模型(EGM2008)[11, 12]，分析了模型阶数、空气阻力和迭代步长等参数对解算轨迹的影响，并着重对落点冗余数据质量控制方案进行了研究。
2 飞行器运行状态方程在地心地固空间直角坐标系中，质量为m的无动力、无控制飞行器运动状态方程可表示为
式中，p和v分别为飞行器位置与速度；g、ac、ae和aaero分别表示引力加速度、科氏加速度、离心加速度以及空气对飞行器产生的加速度。
从状态方程式(1)可以看出，如果给定飞行器初始状态及其受力情况，就可以唯一确定飞行器运行轨迹。由力学知识可知，飞行器所受科氏加速度和离心加速度可用式(2)和式(3)表示
因此，飞行器所受作用力矢量形式为
式中，F为飞行器受力矢量；g为飞行器所处位置引力加速度矢量；ω=[0 0 ω]T为地球旋转角速度矢量；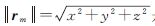
是地心与飞行器间矢径(x、y、z为飞行器在空间直角坐标系中位置坐标)；Faero=FD+FL为空气对飞行器作用力(FD和FL分别为空气阻力与升力，自由段中Faero=0，在零攻角情况下，FL=0)。
通常，飞行器是以任意姿态进入大气层的，其运动包含质心运动和绕质心运动[13]。对于再入式飞行器，当有攻角时，稳定力矩将使攻角减小，通常在气动力较小时就使飞行器稳定下来，速度方向与飞行器纵轴方向重合，攻角为零。此时，飞行器不受升力作用，其受力情况可简化为
空气阻力是物体在空气中运动所产生的，其数值大小与飞行器阻力系数CD(M,h)、参考面积SM(定义为物体在运动方向上投影面积，对于形状规则、无空洞物体，其参考面积即为截面积)、速度v以及空气密度ρ(h)有关[14]，其表达式为
式中，阻力系数CD(M,h)是一个无量纲系数；M=v/v0为马赫数(v和v0分别是飞行器速度及所在位置处音速)；ρ(h)为大气密度，其数值大小主要与高度h有关。
传统上，为了方便计算和加快运算速度，通常采用的引力加速度模型为
如前文所述，引力加速度是影响飞行器运行轨迹的主要因素，而利用式(7)计算的引力加速度精度偏低，无法精确地描述飞行器运行轨迹。最新推出的EGM2008模型最高可展开至2159阶，计算精度代表了目前模型最高精度，其数学模型及应用情况详见文献[15,16]。
综上所述，飞行器被动段运动状态方程可展开成如下形式
式中，当飞行器高度＞90km时，ρ(h)=0kg/m3。
如果给定飞行器质量和形状等参数，再结合t0时刻初始运行状态x0、y0、z0、vx0、vy0、vz0，就可利用数值积分方法解算出飞行器的运行轨迹，并确定其落点位置。在实践中，采集飞行器空间位置信息主要依靠外测和遥测两种手段[17, 18]，遥测需要事先在被观测目标上安装专用设备来传送该目标的相关参数信息，故该观测手段通常用于飞行器试验中。一般情况下，获取飞行器运行状态信息主要依靠外测手段，外测又可分为雷达测量(简称雷测)和光学测量(简称光测)两种方式。目前，雷测是外测手段中精度较高的一种测量方式，这里以该方式为例，对其数据处理方法进行研究。
建立测站直角坐标系，设雷达设备接收天线回转中心天文坐标经度、纬度和距离椭球面高度分别为λ、φ和hs；以该回转中心为坐标系原点Os；Ys轴指向子午线方向(向北为正)；Zs轴指向垂线方向(向上为正)；Xs垂直于Ys轴和Zs轴(向东为正)，构成右手坐标系。设雷达在t0时刻观测飞行器位置参数为距离R0、方位角A0和高度角E0，在测站坐标系中坐标为(xs0,ys0,zs0)。不计观测噪声影响，雷达观测值经过仪器系统误差和电波折射误差修正等数据处理后，有如下表达式
为了将测站坐标系中飞行器的坐标位置转换成地心地固空间直角坐标系中的坐标位置，需要给出二者之间的转换关系，限于篇幅，略去推导过程，直接给出转换关系式如下
式中，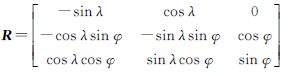
为坐标转换矩阵；
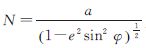为卯酉圈曲率半径；a和e分别是旋转椭球赤道长半径与第一偏心率。
联合式(9)和式(10)，可将雷达观测值R0、A0和E0换算成空间直角坐标系中的位置(xs0,ys0,zs0)。为了求解状态方程式(8)，还需要提供飞行器初始速度参数vx0、vy0、vz0，此时，可根据解算的空间位置信息采用二阶多项式中心平滑微分求得。目前，常用雷达观测设备基本上都具备采集被观测目标距离变化率功能，这时可在微分平滑获取vx0、vy0、vz0的基础上，将观测量应用递推最小二乘估计，获取更为精确的速度信息。
3 落点预报质量控制方案在回收高空飞行器试验中(特别是载人飞行试验)，为了确保人员与飞行器安全，需要根据在轨飞行器当前运行状态信息对其落点位置进行精确预报，该项工作有时需要在飞行器降落地面前数十分钟进行。目前，飞行器落点预报主要采用人机交互方式，即通过计算机计算出若干预示落点，再结合人工经验对飞行器落点进行预报。该方法受人为因素制约较大，不同人员给出的结果存在较大差异，因而其实用性存在一定限制。研究表明，飞行器经过风洞试验可以获取其阻力系数，再根据运行轨迹上任取点运行状态信息(x0、y0、z0、vx0、vy0、vz0)，就可以根据状态方程式(8)计算出落点位置解。理论上，最终落点位置解具有唯一性。但是，由于观测误差、气象环境等因素影响，实际计算得到的落点信息通常为一群离散解，在平面上呈散点状分布，实践中需要根据这些离散解进一步求解落点唯一估值。在随机误差影响下，根据不同时刻飞行状态数据计算的落点结果是比较集中的；反之，当观测数据中包含粗差时，计算的落点结果则是发散的。根据这一特征，本文选取层次聚类分析方法对解算结果进行处理，分以下3个步骤：
(1) 初步分类。如果第i个位置解与第j个位置解的平面位置距离dij小于给定阈值ω，则将第i个位置解与第j个位置解归为同一簇，阈值大小可视时间采样间隔而定。若某位置解与其他所有解平面位置距离都大于给定阈值，则称该位置解为孤立解。孤立解产生的主要原因是飞行器运行状态观测值中包含较大误差(甚至含有粗差)，因此在初步分类中，应对孤立解予以消除。
(2) 修正分类。步骤(1)采用较为苛刻的硬阈值法对位置解进行划分，使得即使是差异较小的位置解也归为不同簇，造成分类过多，为此再采用软阈值法对初步分类结果进行融合处理。视位置解平面坐标总体由一定数量的正态分布混合而成，借助统计检验理论判断两簇重心是否存在显著差异。假定Cm和Cn为初步分类后的两簇，所包含位置解个数分别为Nm与Nn，且方差相同，满足式(11)，说明两簇无显著差异，应合并为一簇，否则认为两者来自不同总体。
式中，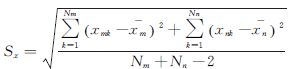
；
；
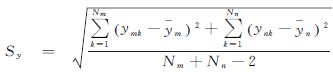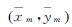与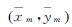分别为Cm和Cn簇平面位置重心位置；(xmk,ymk)与(xnk,ynk)分别为Cm和Cn簇内第k个位置解的平面坐标；tα/2(Nm+Nn－2)是置信度为α、自由度为Nm+Nn－2时t分布临界值。
(3) 消除伪解。初步分类结果经过修正分类后，部分簇所包含的位置解数目较多，有些则较少。由于实际落点附近对应的位置解通常较为密集，而包含位置解数目较少的类簇可能是由噪声或微扰动异常所引起，称其为伪解，因此对于这些伪解应予以淘汰。淘汰原则是对包含位置解个数较多的簇进行比较，如果其中一簇包含数目明显多于其他簇，则该簇重心位置对应飞行器落点位置；如果其中几簇包含个数较为接近，则再结合人工方式进行判读，经过多次实测数据验证表明，该情况发生的概率很小。
4 仿真计算与分析为检验提出的飞行器轨迹解算方法和落点质量控制方案的可行性与有效性，采用仿真数据进行说明。
4.1 要素影响分析飞行器阻力系数除了与自身形状有关外，还与速度以及所处高度等因素有关。一般情况下，当飞行器以超音速在大气层中运行时，其阻力系数大体变化趋势是：运行速度越大，阻力系数越小；所在高度越高，阻力系数越小[19, 20]。实践中，飞行器试验前可通过一系列风洞试验，获取飞行器阻力系数的离散值；在飞行器试验过程中，根据飞行器瞬时高度和速度利用Kringing或三次样条等二维插值方法实时计算其对应的阻力系数，再代入状态方程解算飞行器运行轨迹。
设某飞行器质量为500kg，横截面积为0.5m2，其阻力系数可用多项式表示为
假设雷达在t0时刻捕获飞行器瞬时位置，经转换得其在地心地固空间直角坐标系中坐标为(x0,y0,z0)=(-3131100{3731500,4840 900)，单位为m;速度是(vx0,vy0,vz0)=(-3485.74,-3547.36,360.68)，单位是m/s。设落点处和地心间距离为R，并取|rm-R|≤ε作为解算状态方程式(8)的终止条件。其中，阈值ε取值大小应根据飞行器运行速度v和积分迭代步长τ综合确定，如果ε取值过大，将使得满足终止迭代条件的飞行器落地计算时间提前于实际落地时间，并造成其他参数解算结果存在较大偏差；若ε取值过小，可能使得计算得到的最接近地表处的落点参数也无法满足终止条件，从而导致状态方程无解，这里设ε=v×τ。计算时选取引力加速度模型为120阶EGM2008球谐模型，大气密度及音速模型为1976年美国标准大气模型，数值积分采用四阶龙格—库塔法，积分迭代步长取0.05s。经计算，各作用力对飞行器产生的加速度以及其速度、高度与运行轨迹等变化情况分别如图 1—图 4所示，为简便计，图中以“0”时刻代替t0时刻。
|
| 图 1 在轨高度和速度变化 Fig. 1 he variation of altitude and velocity |
|
| 图 2 引力、科氏和离心加速度变化 Fig. 2 Acceleration of gravitation,coriolis and centrifugal force |
|
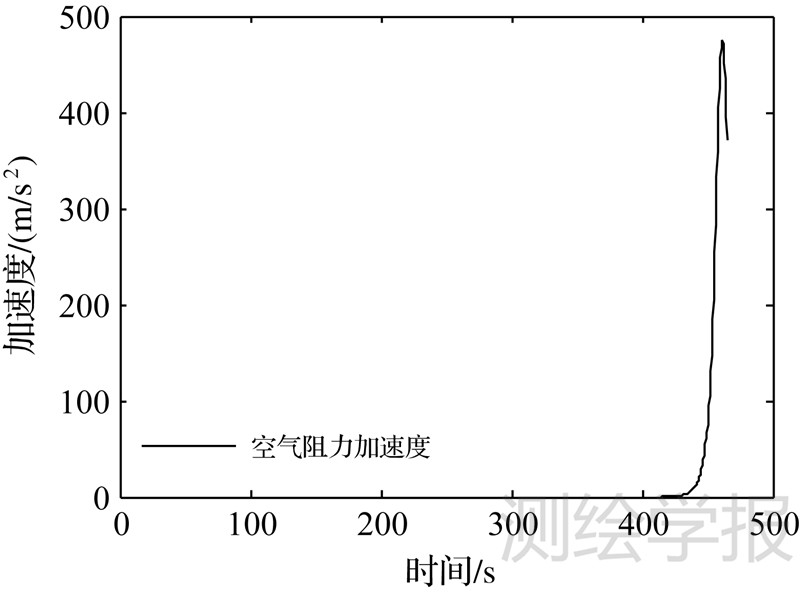
| 图 3 空气阻力加速度变化 Fig. 3 Acceleration of air drag |
|
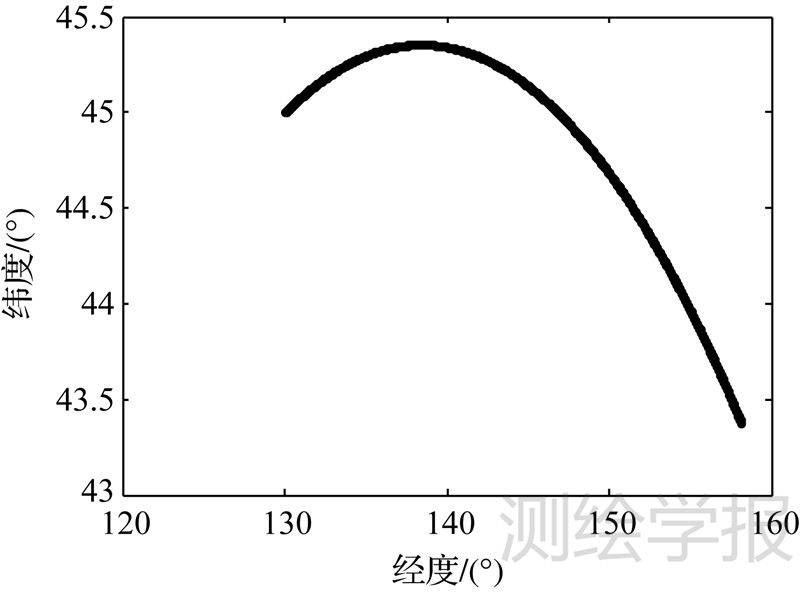
| 图 4 飞行器运行轨迹在地表投影 Fig. 4 The projection of vehicle’s flight trajectory at the earth’s surface |
由图 1可以看到，在上述各力作用下，飞行器在运行过程中，高度由499986.60m减小为0m；速度呈先增大后减小的变化趋势，最大值发生时刻为439.3s，数值是5737.92m/s，在坠落至地表处速度为最小值1793.13m/s。在图 2中，由于科氏加速度与飞行器运行速度成正比关系，在自由段，随着飞行器运行速度变大，科氏加速度也缓慢增加；而在再入段，飞行器受空气阻力作用，速度迅速下降，科氏加速度也快速减小，在整个运行过程中最大值为0.762718m/s2，最小值为0.234112m/s2，平均值为0.737062m/s2。离心加速度主要与飞行器空间位置有关，随着飞行器高度不断下降，离心加速度也逐渐减小，其最大值为0.025902m/s2，最小值为0.024694m/s2，平均值为0.025298m/s2。引力加速度主要和飞行器与地心间距离相关，随着两者之间距离缩小，引力加速度逐渐增大，其最大值为9.822472m/s2，最小值为8.445994m/s2，平均值为8.908313m/s2。可见，在整个飞行过程中，引力加速度影响最大，科氏加速度次之，离心加速度最小。由图 3可知，再入段中空气阻力加速度呈先增大后减小的变化趋势，最大值发生时刻为461s，数值为474.764751m/s2，约为引力加速度的48倍，此时高度为3573.93m，速度是2960.88m/s。经计算，从发现飞行器时刻开始到其落入地表时间间隔应为464.90s，其中再入段中运行时间为49.55s。在此期间，飞行器受各作用力综合影响下运行轨迹在地表投影如图 4所示。可以看到，轨迹在经度方向上不断增加，在纬度方向上先增加后减小，其中飞行器起始时刻地表投影点经度为129.999997°，纬度为45.000091°，最终计算落点位置经度为158.167845°，纬度为43.370071°，两者间大地线长为2248077.67m。
由上述分析可知，再入段中空气阻力是影响飞行器运行轨迹的最主要因素。在飞行器再入段运行轨迹常规解算时，通常的做法是忽略空气阻力影响或将空气阻力系数作为常值进行处理。本文对空气阻力为零这一情况进行了计算，结果为，飞行器从观测时刻开始到落入地表时间间隔为460.05s，计算落点位置经度为158.173531°，纬度为43.368967°，与考虑阻力情况下落点平面位置的点位误差476.90m相比，时间相差4.85s。
引力加速度是影响飞行器全程运行轨迹的重要因素，引力场模型阶数选取多少直接反映了计算精度的高低，即模型阶数越高，引力场计算越精确，飞行器运行轨迹解算精度也越高。然而，实践中不仅需要考虑运行轨迹解算精度，还要顾及实时计算速度，而引力场模型阶数过多，引入计算量便会迅速放大。因此，合理的做法是在保证飞行器运行轨迹解算精度的基础上，尽可能减少引力场模型阶数。为此，计算了引力场模型阶数和飞行器运行轨迹解算精度的关系(试验条件同上)，并以最终落点计算位置对轨迹计算精度进行评估，其结果如表 1所示。
| 阶数 | g最大值 /(m/s2) | g最小值 /(m/s2) | g平均值 /(m/s2) | 时间间隔 /s | 落点经度 /(°) | 落点纬度 /(°) | 点位误差 /m |
| 1 | 9.829117 | 8.451695 | 8.914558 | 464.60 | 158.153947 | 43.385006 | 2005.43 |
| 2 | 9.822734 | 8.445914 | 8.908278 | 464.90 | 158.168032 | 43.370042 | 15.50 |
| 5 | 9.822626 | 8.445869 | 8.908219 | 464.90 | 158.168007 | 43.370046 | 13.42 |
| 10 | 9.822552 | 8.445985 | 8.908304 | 464.90 | 158.167847 | 43.370065 | 0.68 |
| 20 | 9.822563 | 8.446000 | 8.908300 | 464.90 | 158.167838 | 43.370068 | 0.65 |
| 50 | 9.822626 | 8.445995 | 8.908298 | 464.90 | 158.167843 | 43.370073 | 0.27 |
| 100 | 9.822423 | 8.445994 | 8.908297 | 464.90 | 158.167845 | 43.370071 | 0.00 |
| 200 | 9.822488 | 8.445994 | 8.908297 | 464.90 | 158.167845 | 43.370071 | 0.00 |
| 500 | 9.822536 | 8.445994 | 8.908297 | 464.90 | 158.167845 | 43.370071 | 0.00 |
| 1000 | 9.822532 | 8.445994 | 8.908297 | 464.90 | 158.167845 | 43.370071 | — |
由表 1可以看到，随着EGM2008模型阶数的增加，飞行器落点计算位置差异逐渐减小，说明利用该模型解算结果是收敛的，其中10阶以上计算结果差异仅为亚米级。这里取模型阶数为1000时落点计算结果为真值，则模型阶数为1阶和2阶时，计算落点平面位置点位误差分别为2005.43m与15.50m，可见EGM2008模型1阶项和2阶项占整体模型的绝大部分。因此，引力场模型通常取至2阶项即可满足一般情况下飞行器运行轨迹解算的需求，当需要更为精确解算时，可将引力场模型进一步扩展至10阶项左右。
在利用龙格—库塔法对状态方程进行数值积分时，应先确定积分迭代步长。如果选取步长过大，不仅会在节点处增大截断误差，使得解算飞行器运行轨迹存在较大误差，还可能造成满足终止迭代条件的最后一点位置因距离椭球表面过大，导致计算落点位置存在较大偏差，难以满足精度要求。但是，步长选择过小，虽然在每一节点处截断误差得以控制，但一定求解区间内迭代步数将会增加，除了引起计算量增大外，还会导致截断误差大量积累与传播，同样会影响计算结果精度。因此，如何选择步长对于精确解算飞行器运行轨迹是一个关键环节。表 2列出了不同积分迭代步长情况下落点的计算结果(采用120阶EGM2008引力场模型，其他参数选择同上)。
| τ/s | 落地前 时间/s | 落点 经度/s | 落点 纬度/s | 点位 误差/m |
| 10 | 460 | 158.031504 | 43.397947 | 11540.71 |
| 5 | 460 | 158.032915 | 43.397660 | 11422.04 |
| 1 | 464 | 158.148023 | 43.374135 | 1735.69 |
| 0.5 | 464.5 | 158.159456 | 43.371793 | 773.81 |
| 0.1 | 464.9 | 158.167661 | 43.370109 | 82.43 |
| 0.05 | 464.90 | 158.167845 | 43.370071 | 66.93 |
| 0.02 | 464.94 | 158.168468 | 43.369943 | 14.47 |
| 0.01 | 464.94 | 158.168615 | 43.369912 | 2.07 |
| 0.005 | 464.945 | 158.168601 | 43.369916 | 3.28 |
| 0.001 | 464.947 | 158.168640 | 43.369908 | — |
由表 2可知，随着积分迭代步长的减小，飞行器计算落点位置差异也慢慢减小，当迭代步长大于0.001s时，计算结果未出现发散现象。以积分迭代步长为0.001s时的计算结果作为真值，迭代步长介于0.001～0.01s之间时，计算落点位置差异为米级。顾及积分迭代步长每减小一半运算量将增加一倍的关系，通常情况下可将积分迭代步长选为0.02～0.1s，如需精确解算飞行器的运行轨迹，积分迭代步长可选为0.001～0.02s。
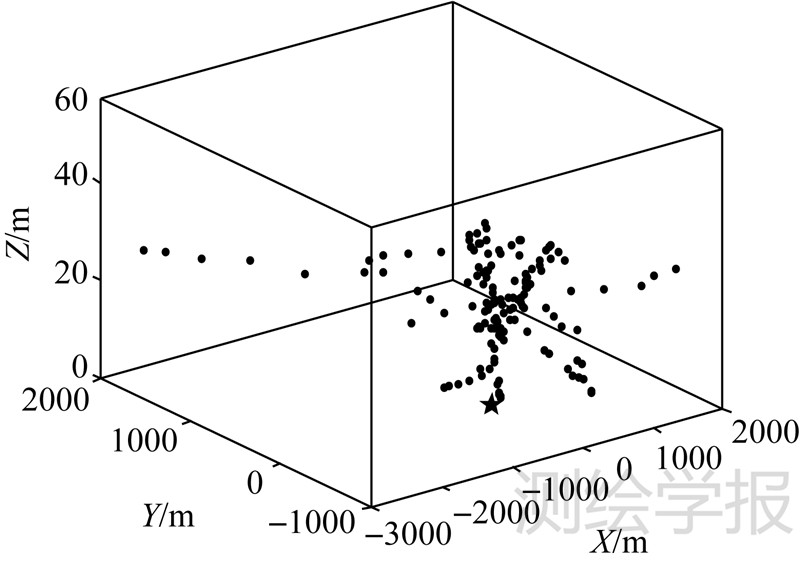
4.2 落点质量控制如前所述，为了精确计算飞行器落点位置，需要根据不同时刻的飞行器观测值计算出落点离散解，经过统计分析等质量控制后予以确定。为了表述理论落点与实际落点的差异，通常要建立以理论落点为坐标原点的落点坐标系，并以该坐标系中纵向偏差和横向偏差来评估飞行器实际落点的平面误差。在此次飞行器观测试验中，设观测时段为71.5s，时间采样分辨率是0.5s，共获取144个采样观测值，引力场模型为120阶EGM2008模型，积分迭代步长为0.02s。经计算，根据144个观测值计算的落点位置在落点坐标系中三维分布如图 5所示，其中“·”和“★”分别表示落点计算位置与理论位置。
|
| 图 5 落点位置三维分布图 Fig. 5 3D distribution graph of impact points |
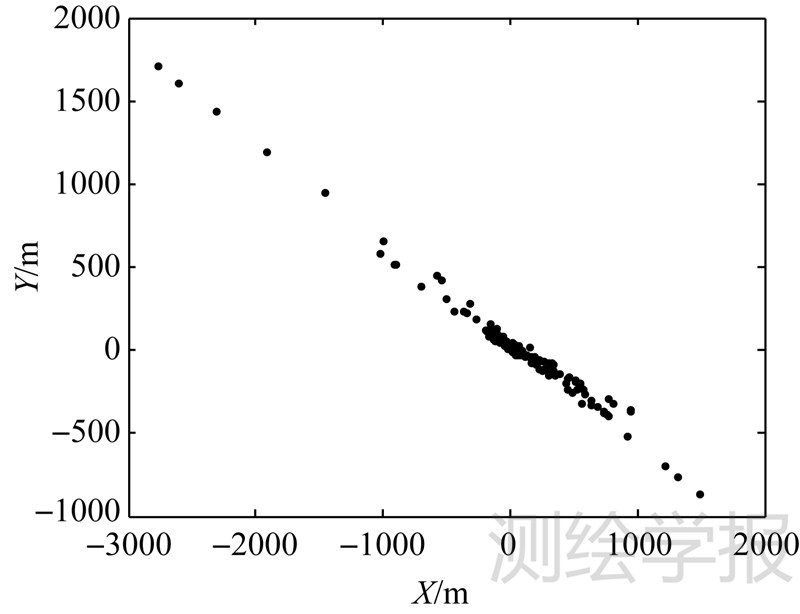
为直观反映质量控制的过程与结果，改用平面分布图分析，144个计算落点位置分布如图 6所示。
|
| 图 6 落点位置平面分布图 Fig. 6 2D distribution graph of impact points |
从分布形态上看，落点位置基本沿着飞行器运行方向呈条带状分布，在靠近理论落点处分布较为集中。在质量控制方案中，首先要给定消除孤立解阈值，取公式如下
式中，
。
经计算，ω数值为34m，消除孤立解后剩余有效解个数为97个，其平面位置分布如图 7所示。
|
| 图 7 消除奇点并初次分类 Fig. 7 First classifying and eliminating isolated point |
经初次分类得25簇，各簇中包含有效解个数如表 3所示。
| 簇号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 有效解个数 | 2 | 2 | 2 | 4 | 2 | 3 | 5 | 5 | 3 | 15 | 5 | 2 | 5 | 2 | 2 | 6 | 3 | 3 | 3 | 5 | 3 | 2 | 3 | 6 | 4 |
在表 3中，共有8簇含有效解最少，均为两个，第10簇含有效解最多，为15个，平均每簇含有3.88个，中误差为2.68个。置式(11)中置信度α＝0.05，经t检验各簇重心差异性，融合修正分类后共有15簇，重新编号后各簇包含有效解个数如表 4所示。
| 簇号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 有效解个数 | 11 | 2 | 2 | 4 | 28 | 13 | 5 | 13 | 2 | 2 | 3 | 3 | 2 | 3 | 4 |
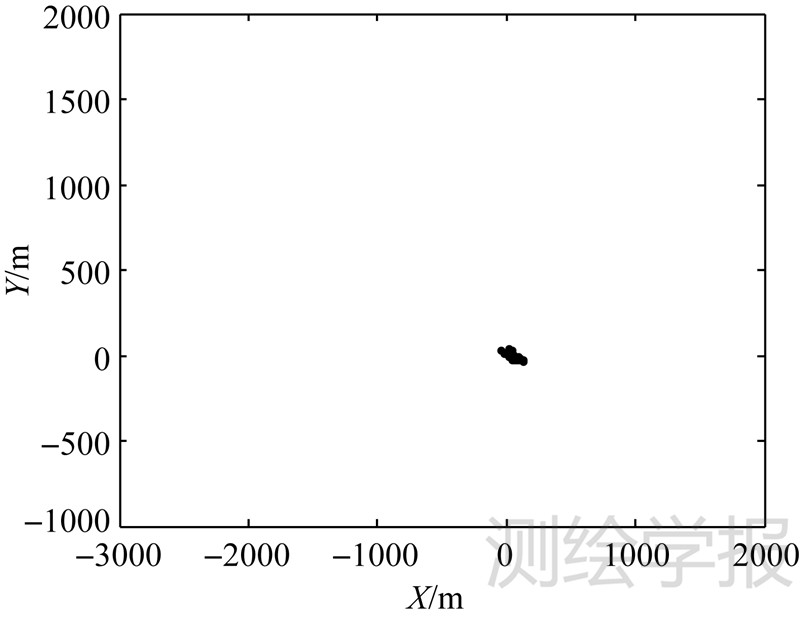
从表 4可以看到，经修正分类后，有效解介于2～5个的共有11簇，介于11～13个的有3簇，第5簇包含有效解最多，为28个(分布状况如图 8所示)，平均每簇包含有效解的个数是6.47个，中误差为7.17个。根据平差理论，选取大于3倍中误差(21.51个)簇的重心作为飞行器落点的最终计算位置，即第5簇重心(图 9中“★”所示)。在落点坐标系中，横向偏差和纵向偏差分别为56.34m与-7.93m。
|
| 图 8 合并分类并删除伪解 Fig. 8 Fusing cluster and eliminating clusters |
|
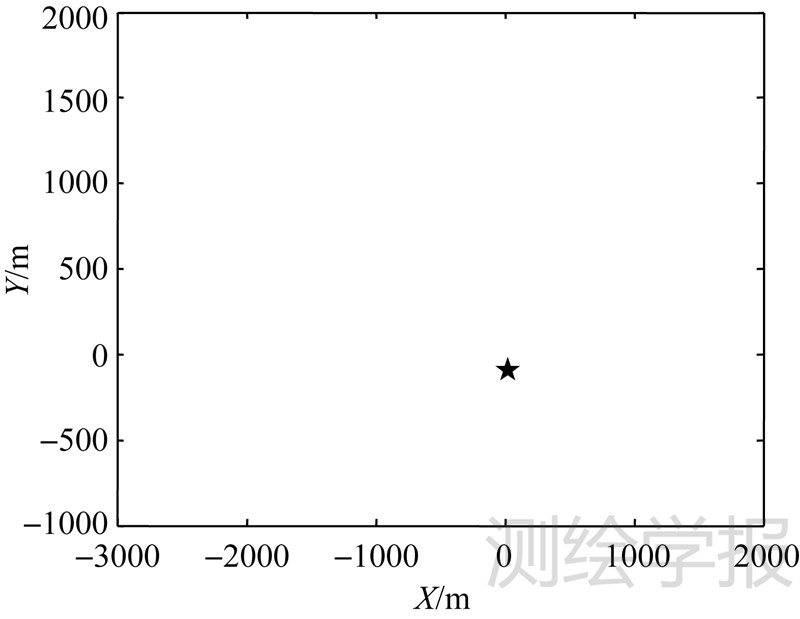
| 图 9 计算得到的飞行器落点位置 Fig. 9 The last position of vehicle |
此外，本文还采用飞行距离数千千米、运行时间数十分钟的飞行器试验实测数据对提出方法适用性进行了验证。结果表明，当采用10阶EGM2008模型，积分迭代步长取0.05s时，经落点质量控制后，计算落点位置与实际落点位置的点位误差可控制在百米以内，计算落点时间与实际落点时间相差量级仅为10-2s，进一步证明了本文方法的有效性。
5 结 论本文在分析无动力、无控制、常质量飞行器空间受力情况的基础上，构建其被动段运动状态方程，研究了空气阻力、地球引力和积分迭代步长等因素对飞行器运行轨迹影响，给出了落点预报质量控制方案，结论表明：
(1) 飞行器运行过程中，地球引力是影响其运行轨迹的主要因素。以EGM2008引力场模型为例，当引力场模型阶数为1阶时，因地球引力引入轨迹误差可达数千米；采用2阶模型时，误差量级可减小至数十米；如果取10阶左右可将误差进一步缩小至亚米级。从中也可以反映出，引力场球谐模型前两项占该模型的绝大部分。
(2) 空气阻力在再入段中对飞行器产生了主要影响。空气阻力加速度在数值上最大可达引力加速度的48倍左右，会给飞行器运行轨迹引入数百米的位置偏差，因此，在飞行器运行状态方程中有必要考虑空气阻力项影响。同时，应根据运算速度及精度因素，合理选择积分迭代步长，当步长介于0.02～0.1s，落点位置计算精度约几十米；积分迭代步长介于0.001～0.01s时，落点位置计算精度为米级。
(3) 落点预报质量控制方案实现了落点位置自动化处理。提出的层次聚类分析方法采用初次分类、修正分类和淘汰伪解3个步骤，有效删除了孤立解，将不同类有效解科学地划分为不同簇，保证了落点位置的准确确定。
本文在轨迹计算与落点预报方面取得了初步的研究成果，但仍然存在一些细节问题需要今后继续深入研究，诸如相关阈值参数最优化确定以及飞行器阻力系数数据库建立等。
| [1] | MINVIELLE P. Decades of Improvement in Re-Entry Ballistic Vehicle Tracking[J]. IEEE: Aerospace and Electronic Systems Magazine, 2005, 20(8):1-14. |
| [2] | LI Y C, THIAGALINGAM K, YAAKOV B S. Trajectory and Launch Point Estimation for Ballistic Missiles from Boost Phase LOS Measurements[C]//Proceedings of the 7th Mediterranean Conference on Control and Automation. Haifa: [s.n.],1999. |
| [3] | FARINA A, RISTIC B, BENVENUTI D. Estimation Accuracy of a Landing Point of a Ballistic Target[C]//Proceedings of the 5th Information Fusion International Conference. Annapolis:[s.n.],2002. |
| [4] | ZHANG Feng, TIAN Kangsheng, XI Mulin. The Ballistic Missile Tracking Method Using Dynamic Model[C]//Proceedings of the 2011 IEEE CIE International Conference. Chengdu:[s.n.],2011,10:24-27. |
| [5] | DODIN P, MINVIELLE P, CADRE J P. Re-Entry Ballistic Vehicle Tracking Observability and Theoretical Bound[C]//Proceedings of the 8th Information Fusion International Conference. Philadelphia: [s.n.],2005:197-204. |
| [6] | TAPLEY B D. SCHUTZ B E, BORN G H. Statistical Orbit Determination[M]. Amsterdam: Elsevier Academic Press, 2004. |
| [7] | AKGVL A, KARASOY S. Development of A Tactical Ballistic Missile Trajectory Prediction Tool[J]. Journal of Electrical & Electronics Engineering, 2005,5:1463-1467. |
| [8] | DODIN P, MINVIELLE P, CADRE J P. Estimation the Ballistic Coefficient of a Re-Entry Vehicle[J]. IET Radar Sonar Navigation, 2007,1(3):173-183. |
| [9] | FORDEN G. GUI_missile_Flyout: A General Program for Simulating Ballistic Missiles[J]. Science and Global Security, 2007, 15(2):133-146. |
| [10] | HARLIN W J, CICCI D A. Ballistic Missile Trajectory Prediction Using a State Transition Matrix[J]. Applied Mathematics and Computation, 2007,188:1832-1847. |
| [11] | QIAN Dong, LIU Fanming, LI Yan, et al. Comparison of Gravity Gradient Reference Map Composition for Navigation[J]. Acta Geodaetica et Cartographica Sinica ,2011,40(6):736-744. (钱东,刘繁明,李艳,等. 导航用重力梯度基准图构建方法的比较研究[J]. 测绘学报,2011,40(6):736-744.) |
| [12] | LIU Xiaogang, WU Xiaoping, ZHAO Dongming, et al.Comparison between Trajectory Disturbing Gravity Calculated with Earth Gravity Field Models of EGM96 and EGM2008[J]. Journal of Geodesy and Geodynamics, 2009,29(5):62-67. (刘晓刚,吴晓平,赵东明,等. EGM96和EGM2008地球重力场模型计算弹道扰动引力的比较[J]. 大地测量与地球动力学, 2009,29(5):62-67.) |
| [13] | CHARLES A B. Investigation of the Performance Characteristics of Re-Entray Vehicles[D]. Alabama:The Air Force University, 2005. |
| [14] | SIOURIS G M, CHEN G R, WANG J R. Tracking an Incoming Ballistic Missile Using an Extended Interval Kalman Filter[J]. Aerospace and Electronic Systems, 1997,33(1):232-240. |
| [15] | ZHANG Chuanyin, GUO Chunxi, CEHN Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica,2009,38(4):283-289. (章传银,郭春喜,陈俊勇,等. EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009,38(4):283-289.) |
| [16] | YANG Jinyu, ZHANG Xunhua, ZHANG Feifei, et al. On the Accuracy of EGM2008 Earth Gravitation Model in Chinese Mainland[J]. Progress in Geophysics, 2012, 27(4): 1298-1306. (杨金玉,张训华,张菲菲,等.EGM2008地球重力模型数据在中国大陆地区的精度分析[J]. 地球物理学进展, 2012, 27(4): 1298-1306.) |
| [17] | MaFarland. Modelling the Ballistic Missile Problem with the State Transition Matrix: An Analysis of Trajectories Including a Rotating Earth and Atmospheric Drag[R]. Virginia Tech. Blacksburg:[s.n.],2004. |
| [18] | LIU C Y, CHEN C T. Tracking the Warhead among Objects Separation from the Re-Entry Vehicle in a Clear Environment[J]. Defence Science Journal, 2009, 59(2):113-125. |
| [19] | ZHANG Yi, XIAO Longxu, WANG Shunhong. Ballistic Missile Trajectory[M]. Changsha: National University of Defense Technology Press,2005,2.(张毅,肖龙旭,王顺宏. 弹道导弹弹道学[M].长沙:国防科技大学出版社,2005.) |
| [20] | LI X R, VESSELIN P, JILKOV. A Survey of Maneuvering Target Tracking—Part Ⅱ: Ballistic Target Models[C]//Proceedings of SPIE Conference on Signal and Data Processing of Small Targets. San Diego:[s.n.],2001. |