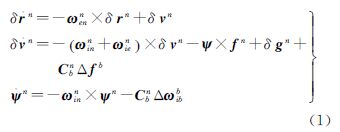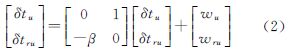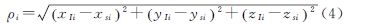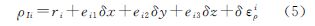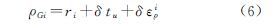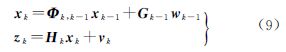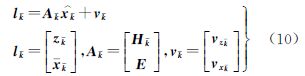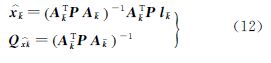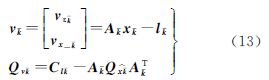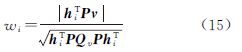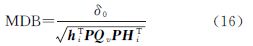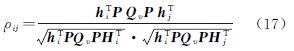2. 同济大学 测绘与地理信息学院,上海 200092
2. College of Surveying and Geo-informatics,Tongji University,Shanghai 200092,China
1 引 言
全球定位系统(GPS)已经被广泛地应用于定位、导航和授时等服务。随着GLONASS、Galileo以及BeiDou系统的完善,下一代全球卫星导航系统(GNSS)的性能将得到极大增强。然而与此同时,系统结构的复杂度也大幅度提升,从而导致故障发生的可能性显著增加,因此其完好性问题成为了普遍关注的研究热点[1, 2, 3, 4]。GNSS系统可靠性研究主要有两个方面,一是GNSS自主完好性监测,主要取决于可见星的冗余度和几何分布情况,因此组合多卫星系统是一种十分有效的途径[1];二是依靠其他导航信息来实现系统的完好性监测,例如在城区建筑物、隧道及桥梁密集的特殊环境中,单纯GNSS系统很难保证导航结果的可靠性[4],此时利用伪卫星、惯性导航(INS)等系统对GNSS系统进行辅助可有效提高其可靠性[5]。
20世纪60年代末,文献[6]最早在大地测量学领域提出了数据探测法并建立了其可靠性分析理论。随后,文献[7—9]在此基础上进一步研究了各局部检验量之间的相关性对检验效果的影响。在GNSS/INS数据处理与导航解算中,针对类似的问题逐渐形成了一套完整的故障检测与隔离(FDI)算法[10, 11]。文献[10]研究了基于预测残差的迭代滤波组合导航的完好性监测方法,文献[11]分析了GNSS/INS组合导航系统中的RAIM算法。文献[12]提出了神经网络算法辅助组合导航系统的故障探测方法。该方法是基于松组合模式,因此,不能对GNSS内部各卫星进行检测与隔离。文献[13]对GPS单系统精密单点定位算法的可靠性进行了研究,对比分析了最小二乘算法与卡尔曼滤波算法在系统内部可靠性及故障检测能力上的差异。文献[14—15]理论分析了多维备选假设检验中局部检验统计量之间的相关性对系统内部可靠性的影响,以及该相关性对GNSS定位精度和抗差性的影响。文献[16—17]考虑了残差之间的相关性,并通过大量统计计算为局部检验法确定更为精确的阈值。
然而,对于GNSS/INS组合导航系统而言,系统的内部可靠性及故障检测能力的强弱由多种因素的相互作用决定,不能一概而论。为此,本文将多GNSS系统与不同精度的INS系统进行组合,由此分析不同因素对组合系统内部的可靠性和故障探测与隔离能力的影响。仿真结果表明,集成多GNSS系统可以改善卫星星座的几何分布结构,从而提高系统的内部可靠性和对故障的区分能力;当GNSS系统与INS系统相结合时,也能大幅度提高系统的可靠性和区分性,并且使系统可靠性不易受卫星的几何结构影响,保持一个稳定状态;相较于低精度的INS系统,采用高精度的INS系统能够进一步地提高系统的可靠性和增强对故障的区分能力,尤其在大机动情况下依然可以保证系统的稳定性,并且可以一定程度上提高系统的导航精度。
2 GNSS/INS紧组合导航系统模型GNSS/INS紧组合导航中,系统的状态分别由INS和GNSS两部分误差状态组成。滤波方程的观测量为INS位置、速度推算得到的伪距、伪距率与GNSS的伪距、伪距率观测值的差值。紧组合导航算法同时可以主要对子系统(INS和GNSS)的误差进行实时补偿[18, 19]。图 1为紧组合导航系统结构图。

|
| 图 1 紧组合导航系统结构图 Fig. 1 Structure of the tight integration navigation system |
导航坐标系(n系)选择当地地理坐标系E—N—U,x、 y、 z轴分别指向当地东、北和垂线向上方向;惯性测量单元固定在载体坐标系(b系),x、y、z轴分别指向右前上方向,文中利用Psi角惯导误差模型,位置、速度和姿态误差方程为[20]
式中,δrn、δvn、ψn分别为导航坐标系下的位置、速度和姿态的误差矢量;fn为导航坐标系下的比力矢量;δgn为重力误差矢量;Cbn为载体坐标系相对于导航坐标系的旋转矩阵;Δfb为载体坐标系下加速度计测量误差矢量;ωien和ωenn分别为地球自转角速度和载体相对于地球旋转角速度;ωinn为ωien和ωenn两者之和;Δωibb为载体坐标系下陀螺测量误差矢量。
GNSS接收机时钟误差模型:接收机钟差δtu,接收机钟漂δtru,其微分方程模型为[18, 19]
式中,β为相关时间;wu和wru为接收机时钟白噪声。
将式(1)和式(2)写成卡尔曼滤波矩阵形式
式中,x包含了导航参数误差项,加速度计和陀螺的常值零偏以及GNSS接收机的钟差和钟漂项;F为状态转移矩阵;G为噪声驱动矩阵;w为系统高斯白噪声[20]。
2.2观测方程设地心地固坐标系中(ECEF),某一时刻INS输出的载体的坐标为(xIi,yIi,zIi),卫星i的坐标为(xsi,ysi,zsi),则可得卫地几何距离为
将式(4)在位置(x,y,z)处进行泰勒级数展开,忽略高阶项,则
式中,ri为载体到第i颗卫星的真实距离;ei1、ei2、ei3为卫星观测方向对3个坐标轴的方向余弦。
采用闭环反馈校正方式进行组合导航,以INS和GNSS的输出的伪距之差作为滤波器的观测量,由式(5)和式(6)得观测方程
因而,得到n颗卫星的导航观测方程为
式中,观测矩阵H=[D 0n×3 0n×3 0n×3 0n×3 -1n×1 0n×1]; ·v为观测噪声。
·v为观测噪声。
式(3)和式(8)对应的离散卡尔曼滤波方程为
式中,xk、xk-1分别为k和k-1时刻的状态向量;Φk,k-1为离散后的状态转移矩阵;Gk-1为k-1时刻噪声驱动矩阵;wk-1为方差是Qk-1的系统白噪声序列;zk为观测向量;Hk为观测矩阵;vk为方差是Rk观测噪声。
3 GNSS/INS完好性基本原理卡尔曼滤波方程式(9)的等价最小二乘形式为[11]
式中,lk为观测向量;Ak为系数矩阵;vk为残差;E为单位矩阵;vzk为观测噪声;vxk为系统噪声。则残差vk的方差-协方差矩阵可由观测噪声矩阵Rk和卡尔曼滤波预测噪声矩阵Pk组成
式中,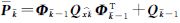 为状态预测的协方差阵。根据最小二乘求得状态参数的最优估计及其协方差矩阵为
为状态预测的协方差阵。根据最小二乘求得状态参数的最优估计及其协方差矩阵为
相应的估计残差及其协方差矩阵为
首先利用全局检验法来判断故障是否发生,构建方差因子[11]
式中,n为观测值维数;u为未知数个数;当系统无故障时,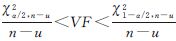 ,VF服从中心化的χ2分布,一旦方差因子大于给定的检验阈值,则判断存在故障,反之则认为无故障发生。
,VF服从中心化的χ2分布,一旦方差因子大于给定的检验阈值,则判断存在故障,反之则认为无故障发生。
通过全局检验法确定故障发生后,进一步利用w检验量对故障进行定位[6, 14]
式中,h=[0…1…0]T,为第i元素是1的单位向量。当该观测值上无故障时,wi服从标准正态分布。
系统的故障检测性能可由内部可靠性指标——最小可探测粗差(MDB)来衡量。MDB是指统计检验中以一定的检验功效所能发现该观测值上的最小粗差[6, 8, 9]
式中,δ0=u1-α/2+u1-β,为非中心化参数;α为显著水平;β为检验功效。本文取α=0.1%,β=20%,因此对应的δ0为4.13。
故障的可区分性表示故障发生在两观测值之间可正确被区分的能力,是由它们之间的相关系数ρij确定的[9, 16]
式中,||ρij||≤1。若两统计量之间的相关系数越大,则发生在这两观测值上的故障就越难被区分。相关性取决于观测值的冗余和几何分布,值得注意的是,当观测值冗余为1时,两两观测值间的相关系数都为1,则粗差只能被探测而不能被区分,因此为保证粗差能够被分离,多余观测量至少为2。
4 计算与分析在GNSS/INS组合导航系统中,根据INS和GNSS不同的数据特性,其故障处理的方式也各不相同,INS故障主要通过增加硬件冗余度来进行识别和隔离,而GNSS故障可以通过前文所述算法进行探测和剔除。本文的数据处理中,认为INS系统是可靠的,重点分析INS系统对GNSS系统的辅助性。本文所有的理论都是基于单个粗差进行假设的,对于多系统造成多粗差的影响将在后续的文章中进行研究。为了评估各种因素对组合系统可靠性及故障检测能力的影响,设计了如下3组试验。
试验1:比较GPS、GPS/GLONASS以及GPS/GLONASS/Galileo 3种解算方案的MDB随时间变化曲线和相关系数的统计情况,目的是为了分析多GNSS系统组合对系统可靠性和故障区分能力的影响。
试验2:计算GPS/INS、GPS/GLONASS/INS、GPS/GLONASS/Galileo/INS 3种解算方案的MDB随时间变化曲线和相关系数统计情况,并与试验1中的相应结果作比较,目的是为了分析加入INS对组合系统可靠性能力的提高程度和相关系数的影响比例。
试验3:计算GPS/INS_LOW、GPS/INS_MED、GPS/INS_HIG 3种解算方案的MDB随时间变化曲线和相关性的变化,目的是为了分析不同精度的惯性导航器件对组合系统可靠性及故障区分能力的影响。对本文仿真数据而言,不同精度惯性传感器的测量值仅存在精度差异,并不考虑因硬件成本的差异造成其出故障的可能性。
以南京某地区(32°02′N,118°51′E,15 m)为例进行数据仿真,GNSS的输出周期为1 Hz,卫星截止高度角为10°,IMU的输出周期为100 Hz,组合周期为1 Hz。仿真中,设计伪距观测噪声为1 m,并模拟3种精度的IMU观测值,分别为Xsens低精度的消费级MTi-G[21],Boeing中等精度的战术级CMIGITS-Ⅱ[22]以及Honeywell高精度的导航级HG9900[23],参数如表 1所示。
| 消费级(LOW)XsensMTi-G | 战术级(MED)Boeing CMIGITS-Ⅱ | 导航级(HIG)Honeywell HG9900 | |
| 加速度计零偏/μg | 2000 | 500 | 25 |
加速度计白噪声/(μg/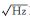 ) ) | 200 | 60 | 1.267 |
| 陀螺零偏/(deg/h) | 20 | 5 | 0.003 |
陀螺白噪声/(deg/ ) ) | 3 | 0.035 | 0.002 |
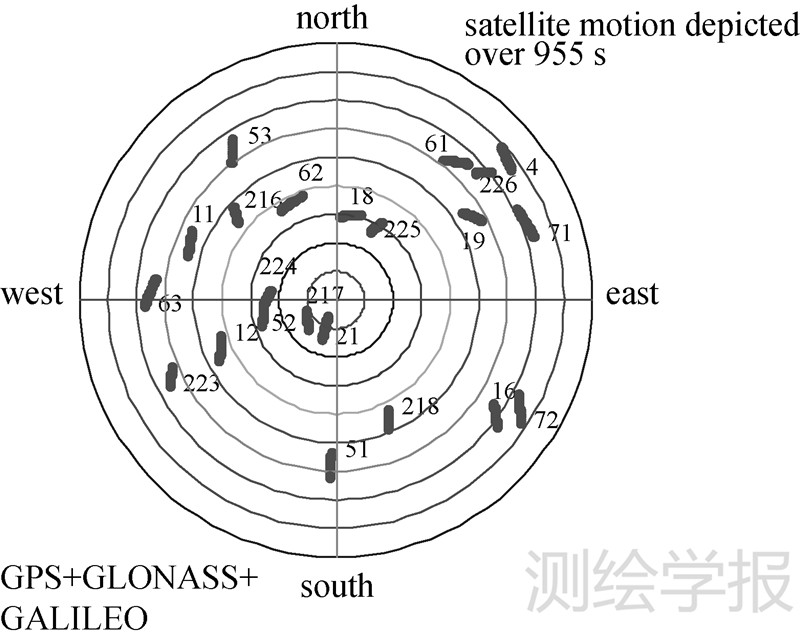
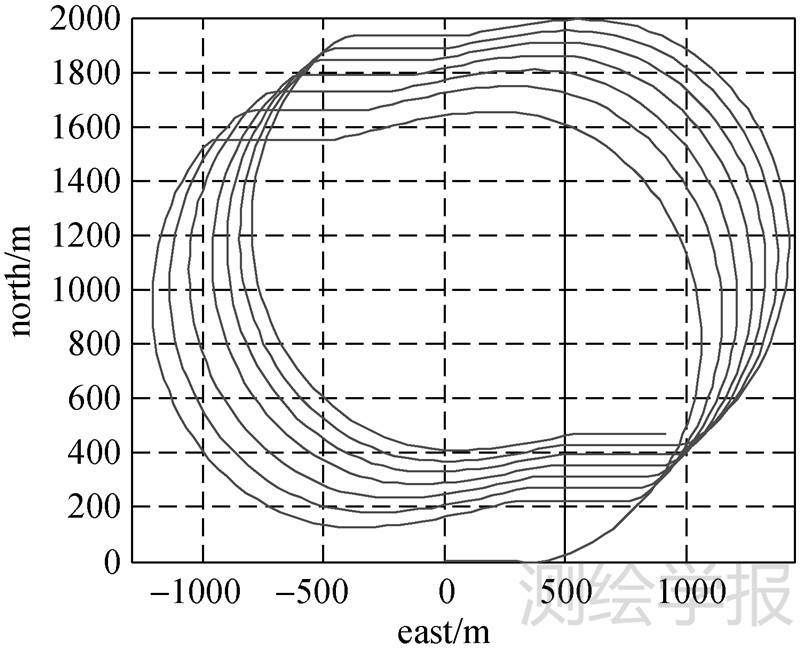
图 2为GPS/GLONASS/Galileo系统的卫星天空可视图,其中PRN号为[4 11 12 16 18 19 21]的是GPS的7颗卫星;GLONASS 8颗卫星的PRN号为[51 52 53 61 62 63 71 72];Galileo 7颗卫星的PRN号为[216 217 218 223 224 225 226]。图 3为仿真的运动参考轨迹。仿真中,载体运动了7圈,每一圈都有两个直线加速和大机动转弯两种运动模式,仿真时间共955 s。
|
| 图 2 卫星天空可视图 Fig. 2 Satellites skyplot |
|
| 图 3 运动参考轨迹 Fig. 3 Tracking reference trajectory |
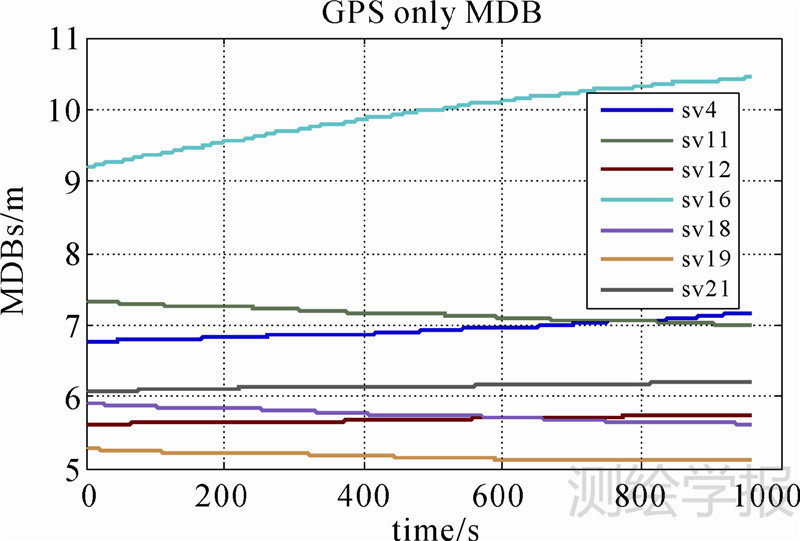
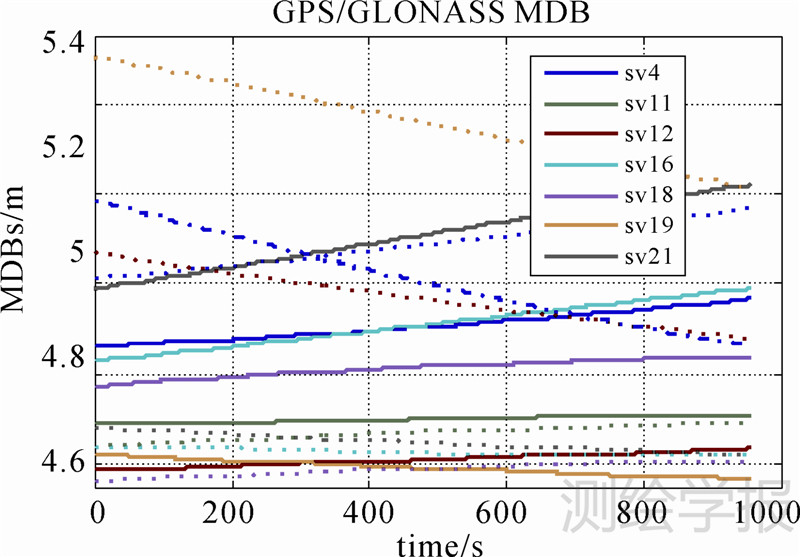
图 4至图 6为各组合方案的MDB随时间变化的曲线。表 2为不同组合方案中GPS第16颗卫星在0时刻和第955 s时刻的MDB值。以GPS第16颗卫星为例,单GPS系统导航解算时,其MDB从9.19 m逐渐增至10.43 m;GPS/GLONASS组合导航解算时,该MDB由4.83 m增至4.99 m;而GPS/GLONASS/Galileo组合时,该MDB仅从4.68 m增至4.78 m。当在单GPS系统中加入GLONASS系统时,系统的内部可靠性提高了近50%。而进一步加入Galileo系统时,系统的内部可靠性也有一定提高。图 4至图 6中,不同卫星的MDB呈现出不同的变化趋势。这是因为GNSS解算中卫星的MDB值受其高度角和几何分布变化的影响。卫星高度角的变化趋势各不相同,有升有降,从而导致MDB有增有减。但依次对比3幅图中的相应曲线可知,融合多个GNSS系统后,各卫星任意时刻的MDB值均有所降低。综合而言,多卫星组合导航系统较单系统能大幅度降低MDB值,从而提高系统的可靠性。
|
| 图 4 GPS单独MDBs Fig. 4 MDBs for GPS only measurements |
|
| 图 5 GPS/GLONASS组合MDBs Fig. 5 MDBs for GPS/GLONASS measurements |

|
| 图 6 GPS/GLONASS/Galileo组合MDBs Fig. 6 MDBs for GPS/GLONASS/Galileo measurements in integration |
| 时刻/s | GPS | GPS/GLONASS | GPS/GLONASS/Galileo | ||
| MDB/m | MDB/m | MDB/m | |||
| 0 | 9.19 | 4.83 | 4.68 | ||
| 955 | 10.43 | 4.99 | 4.78 |
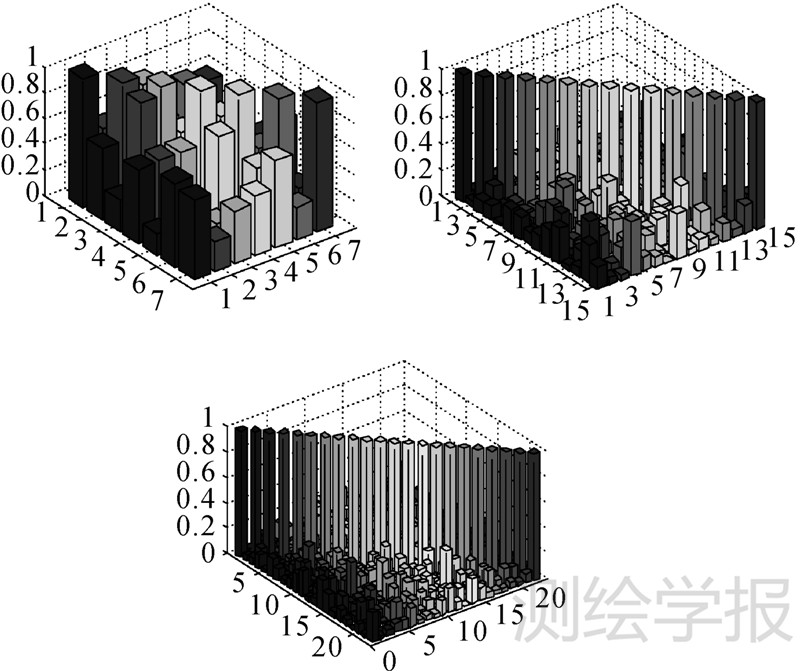
图 7从左至右依次为第100 s时刻GPS、GPS/GLONASS、GPS/GLONASS/Galileo组合导航解算的两两统计量之间的相关系数。该图显示随着卫星冗余度的增加,两两卫星间相关系数明显降低,因而故障的区分能力得到了提高。表 3为整段导航时间内,所有两两卫星间的相关系数的统计结果。从中可知,单GPS系统中,大量的相关系数在0.5以上,甚至存在大于0.8的情况。加入GLONASS卫星后,各卫星间的相关系数显著降低,全部都低于0.5,且95%以上低于0.4;而进一步地集成Galileo时,99%以上的相关系数都在0.3以下。综合而言,多GNSS组合导航系统能够显著改善卫星的几何分布,从而提高系统的抗粗差性能。
|
| 图 7 3种组合方法第100 s两两卫星之间的相关系数比较 Fig. 7 Comparisons for correlation coefficients at epoch 100 among 3 integration methods |
| >0.8 | 0.8~0.7 | 0.7~0.6 | 0.6~0.5 | 0.5~0.4 | 0.4~0.3 | 0.3~0.2 | 0.2~0.1 | <0.1 | |
| G | 955 | 1 116 | 3 647 | 3 285 | 1 630 | 1 191 | 3 982 | 3 294 | 955 |
| G/G | 0 | 0 | 0 | 0 | 2 725 | 5 701 | 12 365 | 30 407 | 49 077 |
| G/G/G | 0 | 0 | 0 | 0 | 0 | 1 910 | 12 495 | 51 484 | 154 716 |
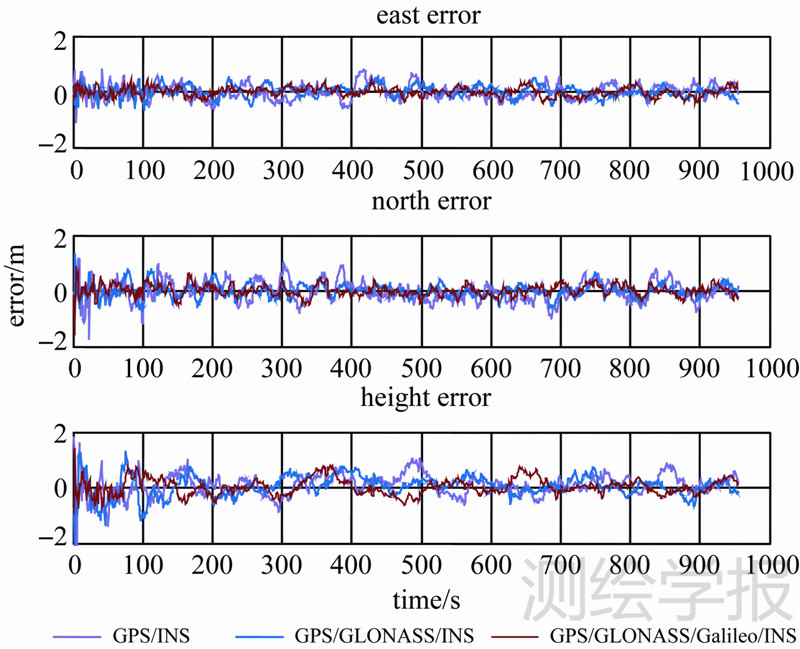
该组试验中INS系统选用Boeing的战术级CMIGITS-Ⅱ进行解算。图 8为3种组合方式导航结果的位置误差,表 4为其相应的误差统计结果。表 5为3种组合方案中导航解算的GPS第16颗卫星在0 s时刻和第955 s时刻的MDB值。图 8至图 10为各组合方案的MDB随时间变化曲线。
|
| 图 8 3种组合方式E-N-U位置误差比较 Fig. 8 Comparisons for E-N-U position errors among 3 integration methods |
| m | |||
| RMS | GPS/INS | GPS/GLONASS/INS | GPS/GLONASS/Galileo/INS |
| 东向位置误差 | 0.276 3 | 0.207 6 | 0.160 1 |
| 北向位置误差 | 0.361 3 | 0.247 9 | 0.210 2 |
| 天向位置误差 | 0.402 1 | 0.374 6 | 0.294 2 |
| 时刻/s | GPS/INS | GPS/GLONASS/INS | GPS/GLONASS/Galileo/INS | ||
| MDB/m | MDB/m | MDB/m | |||
| 0 | 9.03 | 4.82 | 4.67 | ||
| 955 | 4.61 | 4.33 | 4.29 |
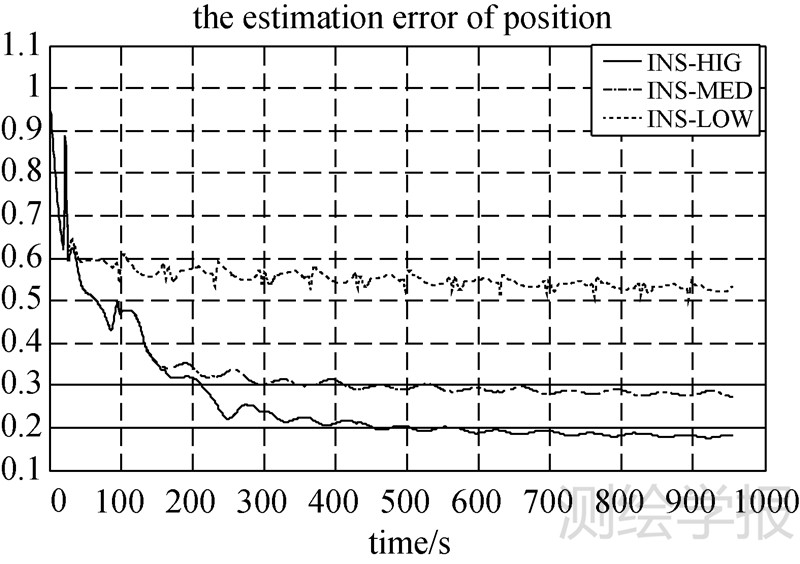
图 7显示3种组合方案的导航精度均在2 m以内。在导航解算刚开始的100 s内,因滤波尚未收敛导致位置误差抖动较大。在100 s之后3种方案的导航解算均收敛至1 m以内。相较而言,GPS/INS解算的位置误差抖动幅度最大,尤其是在机动转弯时有明显的峰值,GPS/GLONASS/Galileo组合解算的位置误差最为平稳。表 4进一步显示,与单独的GPS/INS组合相比,GPS/GLONASS/INS组合导航解算的位置精度提高了33.56%;当继续与Galileo系统组合时,导航解算的位置精度进一步提高了36.16%。
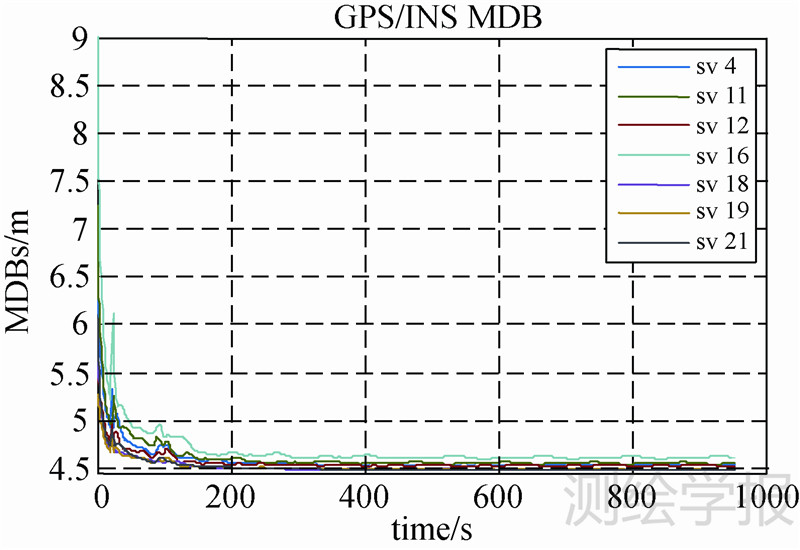
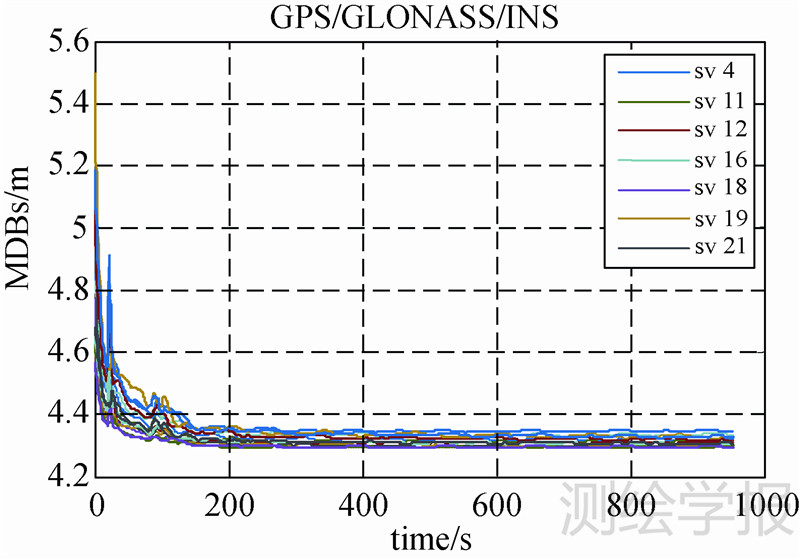
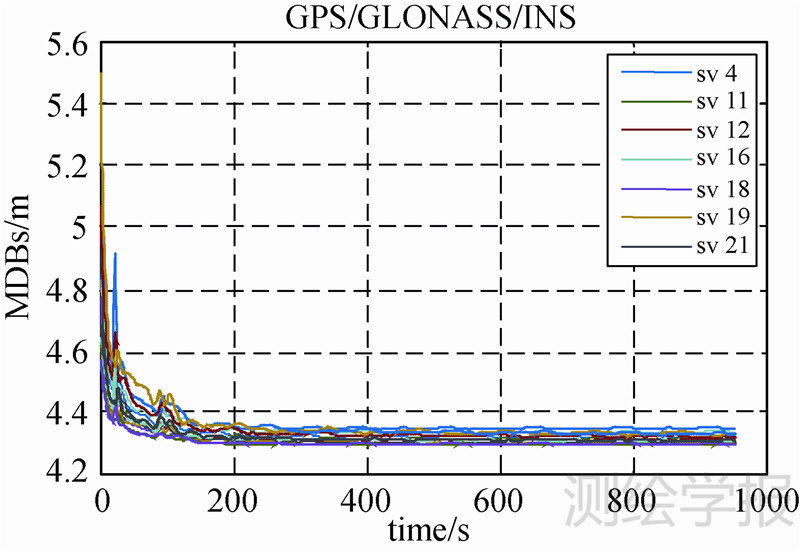
表 5显示GPS/INS组合导航时,GPS第16号卫星的MDB从9.03 m降至4.61 m;GPS/GLONASS/INS组合时,该MDB从4.82 m降至4.33 m;而GPS/GLONASS/Galileo/INS组合时,该MDB由4.67 m降至4.29 m。对比表 5与试验1和表 2中相应位置的数据发现,加入INS之后组合系统的MDB均有所下将。其中最为明显的变化表现在第955 s时GPS单独导航解算的MDB为10.43 m,而加入INS之后这一数值显著降低至4.61 m。图 9至图 11中,各观测卫星的MDB值均随解算时间迅速下降并且收敛,之后保持在一个稳定值上下浮动。这一点显著区别于图 4至图 6的GNSS系统的解算结果。这是因为GNSS/INS组合系统中,各卫星的MDB不仅受到卫星高度角及几何分布的影响,更大程度上依赖于卡尔曼滤波的估计精度。当卡尔曼滤波的解算精度随导航时间收敛后,各卫星的MDB值也相应地趋于稳定。
|
| 图 9 GPS/INS组合的MDBs Fig. 9 MDBs for GPS/INS measurements in integration |
|
| 图 10 GPS/GLONASS/INS组合MDBs Fig. 10 MDBs for GPS/GLONASS/INS measurements in integration |
|
| 图 11 GPS/GLONASS/Galileo/INS组合MDBs Fig. 11 MDBs for GPS/GLONASS/Galileo/INS measurements in integration |
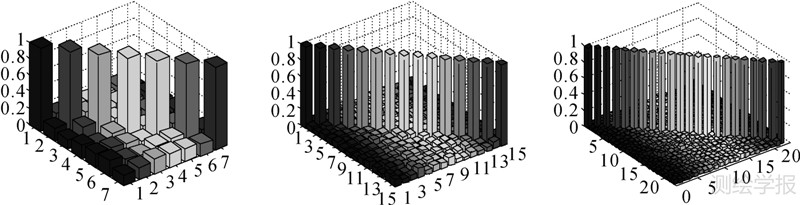
图 12为从左至右依次为GPS/INS、GPS/GLONASS/INS、GPS/GLONASS/Galileo/INS组合导航解算中,第100 s时刻两两卫星间的相关系数。图中所有相关系数均低于0.2,且组合越多的GNSS系统,其相关系数越低。表 6为整个导航时间内,所有卫星两两之间相关系数的统计结果,当GPS/INS组合时,相关系数集中在0.1~0.3,并有少量的相关系数大于0.5;对GPS/GLONASS/INS组合系统而言,所有相关系数均低于0.5,且95%以上都低于0.1;继续组合GPS/GLONASS/Galileo/INS时,相关系数进一步得到降低,99%以上都在0.1以下。
|
| 图 12 3种组合方法第100 s两两卫星之间的相关系数比较 Fig. 12 Comparisons for correlation coefficients at epoch 100 among 3 integration methods |
| >0.8 | 0.8~0.7 | 0.7~0.6 | 0.6~0.5 | 0.5~0.4 | 0.4~0.3 | 0.3~0.2 | 0.2~0.1 | <0.1 | |
| G/I | 1 | 0 | 7 | 10 | 23 | 79 | 1 106 | 17 800 | 1 029 |
| G/G/I | 0 | 0 | 0 | 0 | 3 | 18 | 115 | 4 559 | 95 580 |
| G/G/G/I | 0 | 0 | 0 | 0 | 0 | 5 | 41 | 1 147 | 219 412 |
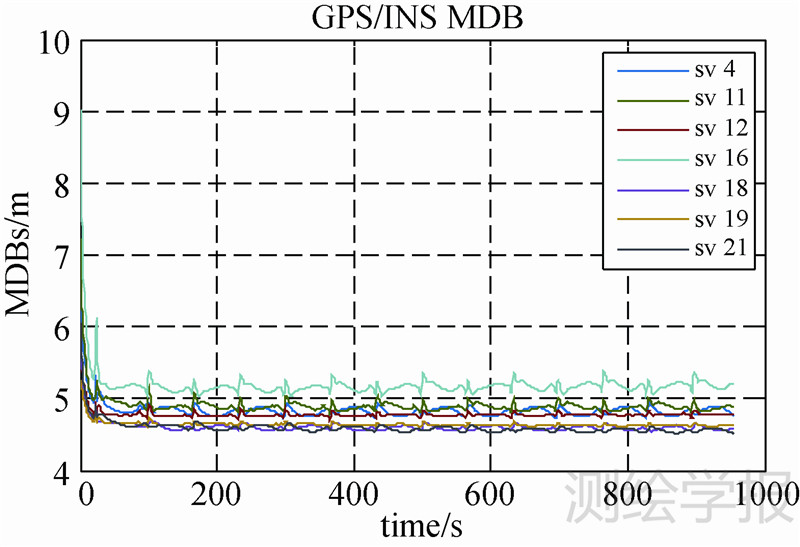
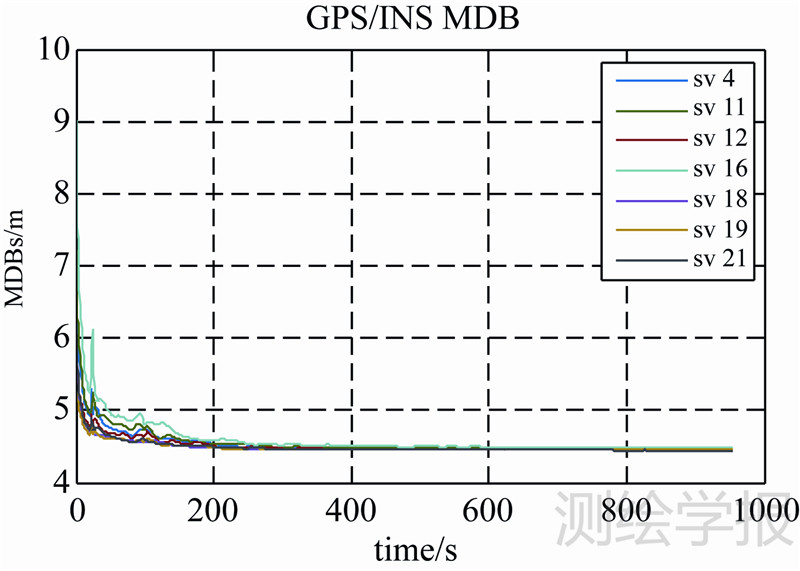
为分析不同精度的惯性导航器件对系统故障识别能力的影响,以第16颗GPS卫星为例(MDB为4.38 m),分析GPS与不同精度的惯导组合时该MDB的变化。试验2中的图 9为GPS/INS_MED的解算结果。图 13和图 14分别为GPS/INS_LOW和GPS/INS_HIG的解算结果。对比3图可知,GPS与消费级惯导系统组合时,该MDB从9.03 m降至5.20 m;与战术级惯导系统组合时,该MDB值降至4.61 m;与导航级惯导系统组合时,该MDB值降至4.48 m。由此可知,惯导系统的精度越高,MDB值越小,但MDB值的降低并不与惯导精度的提高成正比。由式(16)可知,MDB受观测值噪声阵R和残差方差阵Qv的影响,不同精度的惯导系统会造成状态估值的方差阵Q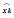 略有不同,并最终影响MDB的取值(由式(11)、式(13)和式(16)可知)。即便不同惯导系统的精度相差103倍,其对Q
略有不同,并最终影响MDB的取值(由式(11)、式(13)和式(16)可知)。即便不同惯导系统的精度相差103倍,其对Q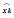 的影响并不会有103倍。这是由卡尔曼滤波中观测值噪声阵R及状态转移噪声阵Q的相互作用决定的。图 15和图 16为滤波过程中方差阵Q
的影响并不会有103倍。这是由卡尔曼滤波中观测值噪声阵R及状态转移噪声阵Q的相互作用决定的。图 15和图 16为滤波过程中方差阵Q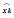 的水平位置和速度对应项的收敛过程。由图可知,对不同精度的惯导系统而言,Q
的水平位置和速度对应项的收敛过程。由图可知,对不同精度的惯导系统而言,Q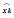 收敛后的速度和位置的估计方差基本在一个数量级上。虽然由惯导精度不同引起Q阵量级相差103倍,最终的导航解算精度却只相差了3倍左右,且中、低精度惯导系统间的差异更小。这也说明了提高惯导精度与MDB的改进能力不成线性递增关系。图 13至16显示,采用低精度惯导系统时的解算结果在载体大幅度转弯时呈现显著抖动,而采用高精度惯导系统可以保证整段运动过程中导航解算的稳定性。总而言之,高精度惯导系统相对于低精度惯导系统更主要的优势是一定程度上能提高导航的精度,当GNSS信号因故缺失时可以保证更长时间的持续导航能力,并保持大机动情况下导航解算的稳定性。此外,从硬件可靠性上考虑,高精度惯导系统出现故障的概率也大大降低。
收敛后的速度和位置的估计方差基本在一个数量级上。虽然由惯导精度不同引起Q阵量级相差103倍,最终的导航解算精度却只相差了3倍左右,且中、低精度惯导系统间的差异更小。这也说明了提高惯导精度与MDB的改进能力不成线性递增关系。图 13至16显示,采用低精度惯导系统时的解算结果在载体大幅度转弯时呈现显著抖动,而采用高精度惯导系统可以保证整段运动过程中导航解算的稳定性。总而言之,高精度惯导系统相对于低精度惯导系统更主要的优势是一定程度上能提高导航的精度,当GNSS信号因故缺失时可以保证更长时间的持续导航能力,并保持大机动情况下导航解算的稳定性。此外,从硬件可靠性上考虑,高精度惯导系统出现故障的概率也大大降低。

|
| 图 13 GPS/INS_LOW组合的MDBs Fig. 13 MDBs for GPS/INS_LOW measurements in integration |
|
| 图 14 GPS/INS_HIG组合的MDBs Fig. 14 MDBs for GPS/INS_HIG measurements in integration |
|
| 图 15 3种不同精度的INS估计的位置方差协方差(RMS) Fig. 15 Position RMS comparisons among 3 different INS systems |
|
| 图 16 3种不同精度的INS估计的速度方差协方差(RMS) Fig. 16 Velocity RMS comparisons among 3 different INS systems |
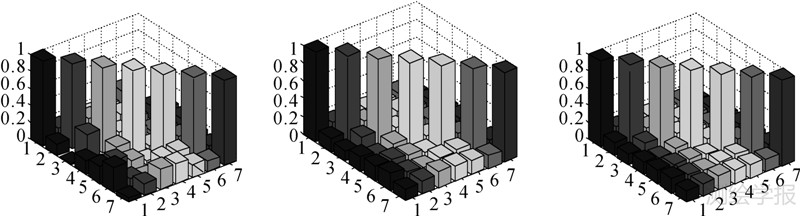
图 17为从左至右依次为第100 s时刻GPS/INS_LOW、GPS/INS_MED、GPSINS_HIG 3种组合导航中两两卫星间的相关系数。该图显示,当提高惯导系统精度时,卫星间的相关性进一步的降低。表 7为整段导航时间内,所有两两卫星间的相关系数的统计结果。表中数据显示惯导系统精度越高相关系数聚集在0.2以下区域的比重越大。对低精度惯导而言,71%以上的相关系数低于0.2,而对中、高精度的惯导系统而言,这一比例分别增至93%和96%。因此,提高惯导精度还可以进一步改善两两卫星间的相关性,从而增强系统对故障的可区分能力。
|
| 图 17 3种组合方法第100s时刻两两卫星间的相关系数 Fig. 17 Comparisons for correlation coefficients at epoch 100 among 3 integration methods |
| >0.8 | 0.8~0.7 | 0.7~0.6 | 0.6~0.5 | 0.5~0.4 | 0.4~0.3 | 0.3~0.2 | 0.2~0.1 | <0.1 | |
| G/IL | 1 | 0 | 7 | 10 | 25 | 758 | 4 921 | 8 576 | 5 757 |
| G/IM | 1 | 0 | 7 | 10 | 23 | 79 | 1 106 | 17 800 | 1 029 |
| G/IH | 1 | 0 | 7 | 10 | 23 | 79 | 621 | 18 524 | 790 |
本文分析了多GNSS系统与各种精度的INS系统组合,并比较了各组合方式在导航精度、可靠性及故障可区分性的能力等方面的区别,得到了以下结论:
(1) 组合GPS、GLONASS和Galileo系统可显著增强卫星星座的几何结构和冗余度,从而提高导航系统的可靠性,并增强系统对故障的可区分能力。
(2) GNSS系统与INS系统相结合也能大幅度提高系统的可靠性和对故障的可区分能力,并且使系统可靠性不易受卫星的几何结构影响。对文中几何精度最差的16号卫星而言,其最小可探测粗差降低了55.8%。
(3) GNSS/INS组合系统中,惯导系统的精度对系统的完好性也有一定影响。战术级IMU相对于消费级IMU的最小可探测粗差降低了0.59 m,导航级IMU相对于战术级IMU的最小可探测粗差降低了0.13 m。
| [1] | OCHIENG W, SHERIDAN K, SAUER K,et al. An Assessment of the RAIM Performance of a Combined Galileo/GPS Navigation System Using the Marginally Detectable Errors (MDE) Algorithm [J]. GPS Solutions, 2002, 5(3): 42-51. |
| [2] | CAI Changsheng, CAO Yang.A Combined GPS/GLONASS Navigation Algorithm for Use with Limited Satellite Visibility [J]. Journal of Navigation, 2009, 62(4): 671-685. |
| [3] | HEWITSON S, KYU L, WANG J. Localizability Analysis for GPS/Galileo Receiver Autonomous Integrity Monitoring[J]. Journal of Navigation, 2004, 57(2): 245-259. |
| [4] | JI Shengyue, CHEN Wu, DING Xiaoli, et al. Potential Benefits of GPS/GLONASS/GALILEO Integration in an Urban Canyon—Hong Kong [J]. Journal of Navigation, 2010, 63(4): 681-693. |
| [5] | ANGRISANO A, PETOVELLO M,PUGLIANO G. Benefits of Combined GPS/GLONASS with Low-cost MEMS IMUs for Vehicular Urban Navigation [J]. Sensors, 2012, 12(4): 5134-5158. |
| [6] | BAARDA W. A Testing Procedure for Use in Geodetic Networks [J].Netherland Geodetic Commission, 1968, 2(5): 1-97. |
| [7] | POPE A. The Statistics of Residuals and the Detection of Outliers [R]. Grenoble:[s.n.], 1976. |
| [8] | FöRSTNER W. Reliability and Discernability of Extended Gauss-Markov Models [C]//Proceedings of Seminar on Mathematical Models to Outliers and Systematic Errors. Munich:[s.n.], 1983, 98: 79-103. |
| [9] | LI Deren,YUAN Xiuxiao.Error Processing and Reliability Theory[M].Wuhan:Press of Wuhan University,2002.(李德仁,袁修孝.误差处理与可靠性理论[M].武汉:武汉大学出版社,2002.) |
| [10] | TEUNISSEN P.Quality Control in Integrated Navigation Systems [C]//Proceedings of Position Location and Navigation Symposium. Las Vegas: IEEE, 1990:158-165. |
| [11] | HEWITSON S, WANG Jinling. GNSS Receiver Autonomous Integrity Monitoring (RAIM) with a Dynamic Model [J]. Journal of Navigation, 2007, 60(2): 247-263. |
| [12] | GAO Weiguang, YANG Yuanxi. Neural Network Aided GPS/INS Integrated Navigation Fault Detection Algorithms [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 403-409.(高为广,杨元喜. 神经网络辅助的GPS/INS组合导航故障检测算法 [J]. 测绘学报,2008, 37(4):403-409.) |
| [13] | XU Changhui, GAO Jingxiang, ZHOU Feng, et al. Reliability Analysis of Precise Point Positioning [J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 709-713.(许长辉, 高井祥, 周锋, 等. 精密单点定位的可靠性研究 [J]. 武汉大学学报: 信息科学版, 2012, 37(6): 709-713.) |
| [14] | YANG Ling, WANG Jinling.Outlier Separability Analysis with a Multiple Alternative Hypotheses Test [J].Journal of Geodesy, 2013, 87(6): 591-604. |
| [15] | YANG Ling, KNIGHT N, LI Yong, et al. Optimal Fault Detection and Exclusion Applied in GNSS Positioning[J]. Journal of Navigation, 2013, 66(5): 1-18. |
| [16] | AYDIN C,DEMIREL H. Computation of Baarda’s Lower Bound of the Non-centrality Parameter [J]. Journal of Geodesy, 2005, 78(7-8):437-441. |
| [17] | AYDIN C. Power of Global Test in Deformation Analysis [J]. Journal of Surveying Engineering, 2012, 138(2):51-56. |
| [18] | WU Fumei, YANG Yuanxi. A New Two-step Adaptive Robust Kalman Filtering in GPS/INS Integrated Navigation System [J].Acta Geodaetica et Cartographica Sinica, 2010, 37(4): 522-527.(吴富梅,杨元喜. 一种两步自适应抗差Kalman滤波在GPS/INS组合导航中的应用 [J]. 测绘学报,2010,39(5): 522-527.) |
| [19] | GEORGY J, NOURELDIN A, GOODALL C. Vehicle Navigator Using a Mixture Particle Filter for Inertial Sensors/Odometer/Map Data/GPS Integration [J]. IEEE Transaction on Consumer Electronics, 2012, 58(2): 544-552. |
| [20] | SOON B, SCHEDING S, LEE H, et al. An Approach to Aid INS Using Time-differenced GPS Carrier Phase (TDCP) Measurements [J]. GPS Solutions, 2008, 12(4): 261-271. |
| [21] | LI Wei, WANG Jinling. Effective Adaptive Kalman Filter for MEMS-IMU/Magnetometers Integrated Attitude and Heading Reference Systems[J]. Journal of Navigation, 2013, 1(1): 1-15. |
| [22] | HAN Songlai, WANG Jinling. Quantization and Colored Noises Error Modeling for Inertial Sensors for GPS/INS Integration[J].IEEE Transactions on Sensors, 2011, 11(6): 1493-1503. |
| [23] | KAUFFMAN K, RAQUET J, MORTON Y, et al. Real-time UWB-OFDM Radar-based Navigation in Unknown Terrain[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1453-1466. |