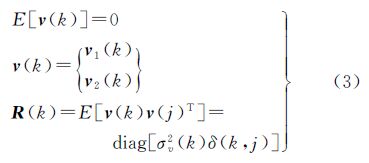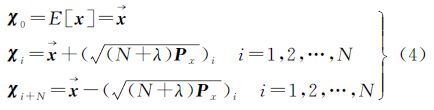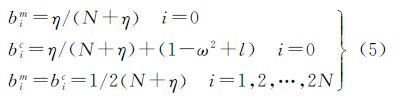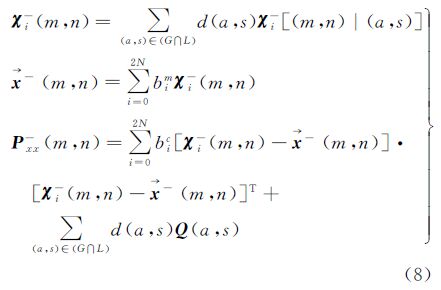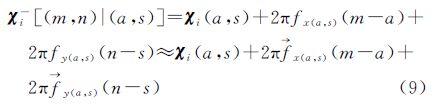干涉相位解缠(或展开、或估计)是InSAR数据处理中的关键环节，一直以来都是InSAR应用技术研究的热点和难点问题[1, 2]。传统相位解缠方法大致可以归纳为以枝切法、网络流法等为代表的路径积分法[3, 4, 5, 6]和以最小二乘法为代表的最小范数法[7, 8, 9, 10, 11]两大类。
经典路径积分算法通过鉴别不连续点(俗称相位残差点)或利用相位质量信息来选择最优解缠路径或孤立相位残差点或掩去可靠性较差的区域，从而解缠其他无相位残差点或可靠性较好的区域。这类方法可以较为精确地解缠相位残差点较少的干涉图，但当干涉图中存在较多的相位残差点时，则存在难以设置合适“积分路径”的问题，有时甚至形成积分路径无法达到的孤立区域，从而导致相位解缠精度下降，甚至完全失效。
最小范数法着眼于整体，利用最优化的思想寻求最小范数意义下的最佳解缠结果，具有计算量较小、数值计算较稳健等特点，但这类方法通常易将变化较为剧烈的相位平滑掉，从而导致其相位解缠精度下降，严重时甚至出现干涉条纹丢失现象，故难以有效解决条纹密集干涉图的解缠问题。随着InSAR技术的发展，多山或陡峭悬崖等复杂地形的高程测量也开始受到了极大关注。然而，复杂地形干涉图条纹通常较为复杂和稀疏不均，非常容易受相位噪声的影响，导致干涉图中存在着大量的相位残差点。为了尽可能地减少干涉图相位残差点数量，降低不连续点给相位解缠过程带来的不利影响，传统相位解缠方法须在相位解缠前须尽可能滤除干涉图中相位噪声[12]。而前置噪声滤波器很难在彻底滤除噪声的同时保持干涉图条纹的边缘特性，这导致传统方法通常难以解决条纹复杂且密集的干涉图的解缠问题。扩展卡尔曼滤波相位解缠算法(EKFPU)[13, 14, 15]和UPF相位解缠算法[16]等方法在完成干涉噪声滤波的同时实现相位解缠，可避免传统方法在相位解缠前须尽可能滤除干涉图中相位噪声的不足。但前者直接对非线性的观测模型做近似线性化处理，损失了高阶相位信息，易导致其相位解缠精度下降，而后者计算代价较大。此外，文献[17]中提出UKF相位解缠方法(UKFPU)。该方法能较为精确地解缠信噪比较高的复杂条纹干涉图，但由于没有与干涉图预滤波算法以及解缠相位后置平滑滤波有效地结合起来，故当干涉图信噪比较低时，该方法性能下降较为严重。
为了进一步解决上述方法易受干涉图条纹稀密程度或干涉图信噪比的制约，难以有效解决条纹密集的复杂地形干涉图的解缠问题，本文把干涉图小窗口预滤波算法与解缠相位后置平滑滤波、全方位局部相位梯度估计技术及传统路径跟踪策略结合起来，提出一种结合滤波算法的UKF相位解缠方法(AUKFPU)。该方法可根据干涉图信噪比情况进行适当预滤波以抑制干涉相位噪声，进而可利用全方位局部相位梯度估计技术较为精确地从复干涉图中提取相位梯度及其估计误差方差等信息，从而有效避免干涉图相位残差点导致的“相位梯度估计欠准”问题，随后利用UKF进行相位解缠，最后再对解缠相位进行平滑滤波以进一步消除解缠相位中的噪声。此外，AUKFPU算法本质上是非线性的，具有比EKFPU算法更高的估计精度，对非线性模型能精确到泰勒级数二阶以上，也不需要计算雅可比矩阵，且计算量仅与EKFPU相当。
2 UKF相位解缠模型用x(k)表示干涉图k像元真实干涉相位，沿某一确定路径用一维坐标k代替二维坐标(m,n)，利用干涉图相邻像元干涉相位之间的关系，以及把归一化的复干涉的同相分量和正交分量分别作为干涉相位的两个观测值，于是可得如下系统方程[17]
式中，u(k)表示干涉图k像元真实相位梯度，实际上是不可能获得的，但可以通过最大似然频率估计器来获得它的估计值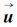
(k)[17]；w(k)为相位梯度估计误差，被认作是高斯白噪声，且满足
式中，σ2w(k)为干涉图k像元相位梯度估计误差方差。式(1)中，z(k)为干涉图k像元复干涉值；a(k)为干涉图k像元复干涉幅度；v1(k)和v2(k)被看作是高斯白噪声，有
式中，σ2v(k)可以由下式计算：
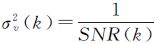，SNR(k)表示复干涉图k像元信噪比。
3 UKF相位解缠算法
3.1 一维UKF解缠算法[17]EKF算法是一种处理非线性问题的线性化方法，通常只使用非线性函数泰勒级数的第一阶，更高阶的展开量因为其较高的复杂度而很少被使用，这导致其高阶信息丢失，直接影响了EKF算法估计精度。UKF算法正是为了克服EKF算法这一缺点而被提出来的，它使用Sigma点来捕捉随机变量的后验均值和方差[18, 19, 20, 21]。
对于状态变量x∈CN×1，x的Sigma点可以表示为
式中，Px和(
)i分别表示状态变量x的估计误差协方差矩阵以及(N+λ)Px均方根矩阵的第i列向量，其相应权值系数为
式中，N表示状态变量x的维数(本文中N=1)；η=ω2(N+κ)－N，参数ω、l、κ用来调节Sigma点，通常可以取ω=0.01，l=2，κ=0[19, 20, 21]。
利用前述UKF相位解缠系统模型，设干涉图k像元的状态估计及其估计误差协方差分别为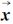
(k)和Pxx(k)，则其预测公式表示为
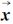－(k+1)分别表示干涉图k+1像元Sigma点的预测值及干涉图k+1像元状态预测值；Q(k)和Pxx－(k+1)分别表示干涉图k像元相位梯度估计误差方差及干涉图k+1像元预测误差协方差。与此同时，UKF相位解缠算法更新公式可以表示为
式中，Pxx－(k+1)表示干涉图k+1像元预测误差协方差；y(k+1)和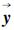
－(k+1)分别表示干涉图k+1像元观测值及预测值；
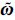(k+1)表示干涉图k+1像元增益矩阵；R(k+1)表示干涉图k+1像元测量误差方差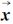；(k+1)和Pxx(k+1)分别表示干涉图k+1像元状态估计值及其估计误差方差。通过式(6)和式(7)，即可实现一维UKF相位解缠算法，同时完成干涉相位噪声滤波与相位解缠。
3.2 结合预置滤波的二维UKF相位解缠算法(AUKFPU)
3.2.1 全方位局部估计与二维UKF相位解缠算法[17]
把不敏卡尔曼滤波与传统路径跟踪策略结合起来，利用相位质量图(如微分偏差图，相关系数图等)引导不敏卡尔曼滤波器沿干涉图高质量区域到低质量区域的路径工作，从而避免直接穿过干涉图低可靠性区域导致的相位解缠精度下降。具体实现方法如下：首先，利用相位质量图(本文采用微分偏差图)，把干涉图可靠性较高区域某一像元作为起始像元，且设定其估计误差，并把与它直接相连的相邻像元列入待解缠像元矩阵之中；其次，对微分偏差最小的待解缠像元进行状态估计以获取其状态估计值
(k)及估计误差方差Pxx(k)，随即在待解缠像元矩阵中删除已解缠像元，并把与之直接相连的未解缠像元列入待解缠像元矩阵之中；最后，检测是否还有待解缠像元，若存在则重复上述第2步，若不存在则结束。
为了更有效利用相邻已解缠像元信息以达到提高估计精度的目的，在二维UKF相位解缠算法中，任一待解缠像元干涉相位预测值可由其相邻8个像元中已解缠像元相位估计值的优化加权而取得。于是，用二维坐标(m,n)代替一维k，则在二维UKF算法中仅有预测公式(6)需要修正为如下
式中，L和G分别指整个干涉图和待解缠像元已解缠邻域(即待解缠像元相邻8点中的已解缠像元)；χi－[(m,n)|(a,s)]指通过干涉图(a,s)像元估计得到的待解缠像元干涉相位的Sigma点的预测值，可以表示为 式中，fx(a,s)和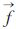
x(a,s)分别为以干涉图(a,s)像元为中心窗口列方向真实局部频率以及通过最大似然频率估计器获得的估计值；而fy(a,s)和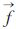y(a,s)分别为行方向真实局部频率及其估计值,其误差克拉美罗界为[22]
式中，Bm和Bn分别为干涉图局部窗口行方向和列方向的长度；r(a,s)为以干涉图(a,s)像元为中心的局部区域相关系数，根据上式很容易得出局部相位梯度估计误差方差。此外，式(8)中d(a,s)指优化权系数，可以表示为
式(11)表明信噪比较低且估计误差较大的相邻已解缠像元，则对当前待解缠像元的预测贡献较小；SNR(a,s)表示复干涉图(a,s)像元信噪比;g(a,s)取0或1，1表示干涉图(a,s)像元已解缠，0表示干涉图(a,s)像元未解缠。
3.2.2 干涉图小窗口预滤波与解缠相位后置平滑滤波矩形均值滤波具有简单快速、相位噪声抑制能力较为明显的特点，是目前最常用的干涉图滤波方法。窗口为(2M+1)×(2N+1)的均值滤波器为
式中，φ(i,j)表示干涉图在像素坐标i,j的相位值；
(m,n)表示滤波后相位。矩形均值滤波不足之处是随着滤波窗口的增大在干涉图条纹密集的局部区域容易出现条纹模糊，但由于UKF算法本身具有一定的噪声抑制能力，所以不必像传统相位解缠方法须在相位解缠之前尽可能完全消除干涉相位噪声，而是仅用小窗口均值滤波器适当抑制干涉图中的相位噪声，以确保干涉图条纹大致清晰即可，既可以降低预滤波复杂度与难度，又能保持干涉图条纹边缘特性，从而不损失干涉图条纹细节信息，为后续的精确相位解缠提供了基础。此外，考虑到尽管UKF相位解缠方法能在相位解缠的同时进行噪声抑制，克服了传统方法在相位解缠之前须尽可能去除干涉图中相位噪声的不足，但有时却较难彻底滤除干涉图中相位噪声。故通常可利用一个小窗口滤波器对UKF解缠相位进行适当平滑滤波，以进一步消除已解缠相位中的噪声，达到进一步增进相位解缠精度的目的。
4 试验结果与分析
4.1 仿真干涉图解缠试验与分析
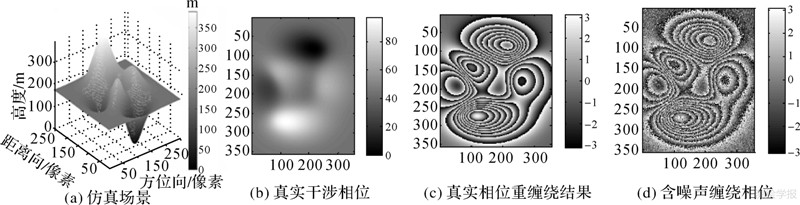
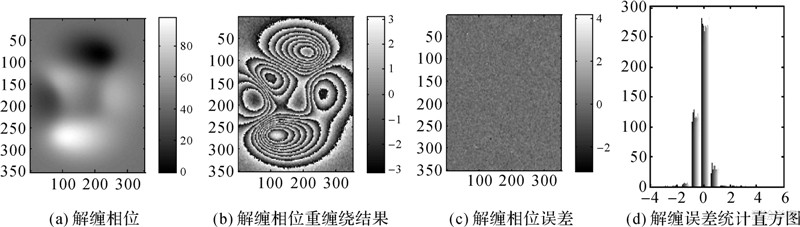
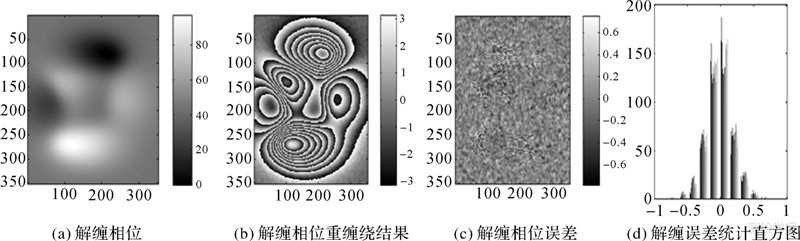
4.1.1 多山地形干涉图解缠试验为了验证本文算法性能和与其他方法进行比较，对一幅锥形场景作模拟成像干涉，即可获得一幅具有复杂条纹的干涉图。仿真参数如下：轨道高度为590 km，下视角为45°，波长为0.03 m，基线倾角为10°，地面分辨率为8 m×8 m，基线长度为350 m。仿真场景见图 1(a)，真实干涉相位见图 1(b)，真实干涉相位重缠绕图见图 1(c)，含噪声干涉图见图 1(d)，其信噪比为3.1 dB。EKFPU算法与UKFPU算法不受相位残点的影响同时完成噪声抑制与相位解缠，其解缠误差主要集中在[-1, 1]附近，解缠结果见图 2(a)—(d)，图 3(a)—图 3(d)。但由于EKFPU方法和UKFPU方法没有与干涉图滤波算法结合起来，故上述方法不能完全消除干涉图中的相位噪声，以致于其重缠绕相位图部分区域仍存在部分噪声，即重缠绕相位图条纹边缘存在毛刺现象，见图 2(b)和图 3(b)。本文AUKFPU算法不仅在全方位局部相位梯度估计中引入相邻已解缠像元信噪比对待解缠像元权重的贡献，而且把二维UKF相位解缠算法与干涉图预滤波算法及解缠相位后置平滑滤波算法等结合起来，利用一个窗口为3×3的均值滤波器对含噪声干涉图进行滤波，解缠相位图及其重缠绕图条纹较为平滑，且与真实干涉相位图及其重缠绕结果是非常一致的，见图 4(a)和图 4(b)。故本文AUKFPU方法解缠误差范围更小，且主要误差集中在[-0.5，0.5]，见图 4(c)和图 4(d)。需要注意的是本文AUKFPU方法中之所以采用小窗口的预滤波器，是因为待解缠干涉图条纹较为复杂，且部分区域条纹密集，而较大窗口的滤波器易导致干涉图条纹密集区域的干涉条纹边缘特性丢失，造成解缠结果失效。
|
| 图 1 仿真干涉图 Fig. 1 Synthetic interferogram over a peak |
|
| 图 2 EKFPU方法解缠结果 Fig. 2 The solution of the EKFPU algorithm |
|
| 图 3 UKFPU方法解缠结果 Fig. 3 The solution of the UKFPU algorithm |
|
| 图 4 本文AUKFPU方法解缠结果 Fig. 4 The solution of the AUKFPU algorithm |
图 5(a)和图 6(a)分别为斜坡和金字塔地形干涉图(仿真参数同上一节的多山地形仿真干涉图相同)，信噪比为0 dB。本文方法解缠斜坡和金字塔地形干涉图结果分别见图 5(b)—(c)和图 6(b)—(c)，可以看出本文方法有效地完成了上述缠绕相位图的解缠工作。
|
| 图 5 本文AUKFPU方法解缠斜坡地形干涉图结果 Fig. 5 The AUKFPU solution to the interferogram over a slope |
|
| 图 6 本文AUKFPU方法解缠金字塔地形干涉图结果 Fig. 6 The AUKFPU solution to the interferogram over a pyramid |
图 7(a)为经5×5均值预滤波处理后的意大利火山干涉图。本文AUKFPU方法解缠相位图及其重缠绕结果见图 7(b)和图 7(c)，可以看出本文方法解缠相位图较为光滑，且其重缠绕条纹与原始干涉条纹完全一致，这表明本文方法已有效地完成了上述缠绕相位图的解缠工作。
|
| 图 7 本文AUKFPU方法解缠Etna火山干涉图结果 Fig. 7 The solution of the AUKFPU algorithm |
本文AUKFPU算法以及EKFPU算法、UKFPU算法等方法是同属贝叶斯框架下的相位解缠算法，其计算量大致相当。由于本文AUKFPU方法与干涉图预滤波算法以及解缠相位后置平滑滤波算法结合在一起，故在相关数据处理试验中获得了优于EKFPU算法以及UKFPU算法等方法的结果。
| [1] | LIU Guolin, DU Zhixing, XUE Huaiping, et al. Application of Kalman Filters to Noise Eliminating and Phase Unwrapping of InSAR [J]. Journal of Geodesy and Geodynamics, 2006, 26(2):64-67. (刘国林,独知行,薛怀平,等.卡尔曼滤波在InSAR噪声消除与相位解缠中的应用[J].大地测量与地球动力学,2006, 26(2):64-67.) |
| [2] | LIU Guolin, HAO Huadong, TAO Qiuxiang. Kalman Filter Phase Unwrapping Algorithm and Comparison and Analysis with other Methods [J]. Geomatics and Information Science of Wuhan University, 2010, 35(10):1174-1178.(刘国林,郝华东,陶秋香.卡尔曼滤波相位解缠及其他方法的对比分析[J].武汉大学学报:信息科学版,2010,35(10):1174-1178.) |
| [3] | GOLDSTEIN R M, ZERBER H A, WERNER C L. Satellite Radar Interferometry: Two-dimensional Phase Unwrapping [J]. Radio Science, 1988, 23 (4):713-720. |
| [4] | COSTANTINI M. A Novel Phase Unwrapping Method Based on Network Programming [J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36 (3): 813-821. |
| [5] | FLYNN T J. Consistent 2-D Phase Unwrapping Guided by a Quality Map [C]//1996 International Geoscience and Remote Sensing Symposium (IGRASS).Lincoln: IEEE,1996:124-134. |
| [6] | CHING N H, ROSENFELD D, BRAUN M. Two-dimensional Phase Unwrapping Using a Minimum Spanning Tree Algorithm [J]. IEEE Transactions on Image Processing, 1992, 1(3), 355-365. |
| [7] | PRITT M D. Phase Unwrapping by Means of Multigrid Techniques for Interferometric SAR [J]. IEEE Transaction on Geoscience and Remote Sensing, 1996, 34(3):728-738. |
| [8] | GHIGLIA D C, ROMERO L A. Minimum LP-norm Two Dimensional Phase Unwrapping [J]. Journal of the Optical Society of America A, 1996, 13(10): 1999-2013. |
| [9] | GHIGLIA D C, ROMERO L A. Robust Two-dimensional Weighted and Unweighted Phase Unwrapping that Uses Fast Transforms and Iterative Methods [J]. Journal of the Optical Society of America, 1994, 11(1):107-117. |
| [10] | QIAN Xiaofan, ZHANG Yong'an, LI Xinyu, et al. Phase Unwrapping Algorithm Based on Mask and Least-squares Iteration[J]. Acta Optica Sinica, 2010, 30(2):440-444. |
| [11] | KAUFMANN G H, GALIZZI G E, RUIZ P D. Evaluation of a Preconditioned Conjugate-gradient Algorithm for Weighted Least-squares Unwrapping of Digital Speckle-pattern Interferometry Phase Maps [J]. Applied Optics, 1998, 37(14):3076. |
| [12] | WENG Jingfeng, LO Yulung. Robust Detection Scheme on Noise and Phase Jump for Phase Maps of Objects with Height Discontinuities: Theory and Experiment [J]. Optics Express, 2011,19(4):3086-3105. |
| [13] | LOFFELD O, KRAEMER R. Phase Unwrapping for SAR Interferometry-a Data Fusion Approach by Kalman Filtering[C]//1999 International Geoscience and Remote Sensing Symposium (IGARSS).Hamburg:IEEE,1999: 1715-1717. |
| [14] | HOLGER N, LOFFELD O, ROBERT W. Phase Unwrapping Using 2D-Kalman Filter Potential and Limitations [C] //2008 International Geoscience and Remote Sensing Symposium (IGARSS).Piscataway: IEEE, 2008: 1213-1216. |
| [15] | LOFFELD O, NIES H, KNEDLIK S, et al. Phase Unwrapping for SAR Interferometry: A Data Fusion Approach by Kalman Filtering [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1):47-58. |
| [16] | XIE Xianming, PI Yiming, PENG Bao. Phase Unwrapping Algorithm: An Unscented Particle Filtering Approach [J]. Acta Electronica Sinica, 2011, 39(3):705-709. (谢先明,皮亦鸣,彭保.一种基于UPF的干涉SAR相位展开方法[J].电子学报, 2011, 39(3):705-709.) |
| [17] | XIE Xianming, PI Yiming. A Phase Noise Filtering, and Phase Unwrapping Method Based on Unscented Kalman Filter [J]. Journal of Systems Engineering and Electronics, 2011, 22(3):365-372. |
| [18] | JULIER S J, UHLMANN J K. Unscented Filtering and Nonlinear Estimation [J]. IEEE Aerospace and Electronic Systems, 2004, 92(3): 401-422. |
| [19] | YANG Jun. Particle Filter Algorithm Research and Application [D]. Xi’an: Xi’an University of Technology, 2008. (杨裙.粒子滤波算法研究及应用[D].西安:西安理工大学, 2008.) |
| [20] | FAN Wei, LI Yong. Precision Analysis of Sigma-point Kalman Filtering Method [C] //Proceedings of 2009 Chinese Control and Decision Conference.Guilin:[s.n.],2009. (范炜,李勇. Sigma点卡尔曼滤波方法精度分析[C] //2009中国控制与决策会议论文集.桂林:[s.n.], 2009.) |
| [21] | MA Ye, WANG Xiaotong, DAI Yao. Study on Nonlinear Optimal Estimation for Neural Networks Data Fusion [J]. Acta Electronica Sinica, 2005, 33(10):1915-1916. (马野,王孝通,戴耀.基于UKF的神经网络自适应全局信息融合方法[J].电子学报,2005,33(10):1915-1916.) |
| [22] | WU Nan, FENG Dazheng, LIU Baoquan. Phase Unwrapping Approach Based on Local Frequency Estimation and Finite Element Method for Interferogram[J]. Journal of System Simulation, 2007, 19(19):4574-4578. (武楠,冯大政,刘宝泉.基于局部频率估计和有限元的相位展开方法[J].系统仿真学报, 2007,19(19):4574-4578.) |