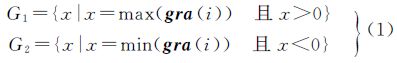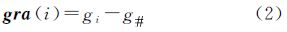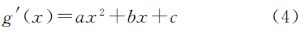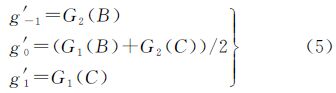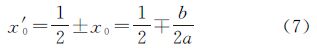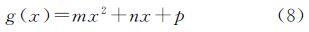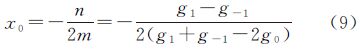2. 河南工业大学 粮食信息处理与控制教育部重点实验室,河南 郑州 450052
2. Key Laboratory of Grain Information Processing and Control of Ministry of Education,Henan University of Technology,Zhengzhou 450052,China
1 引 言
作为图像最基本的特征,边缘有较强的稳定性,并且包含了目标的诸多有用信息,可以为目标的描述与识别以及图像的解译提供有价值的重要参数信息。因此,边缘检测是遥感影像分割、目标识别及地物提取等领域的核心技术,但也一直是计算机视觉、数字摄影测量等领域的难点之一[1]。在诸多经典梯度算子的基础上,基于信号处理[1, 2, 3]、人工智能[4]、分形[5]及形态学[6]等理论的新方法不断涌现。
随着计算机视觉技术在各领域的应用不断深入,人们期望在现有影像数据的条件下,获取目标更精确的位置及尺寸信息,亚像素边缘检测已成为一个研究热点,目前常用的亚像素边缘检测算法可分为插值法[7, 8]、拟合法[8, 9]和矩方法[10, 11, 12, 13, 14]等几类。插值法重复性好,计算量小,但抗噪声能力差,定位精度较低。文献[15]在插值法的基础上,利用改进水平集重构的方法在保持亚像素精度的同时消除了插值法产生的锯齿效应,得到了平滑的边缘,但计算量大。拟合法精度较高,对噪声不敏感,但其模型复杂求解速度较慢,并且要求边缘满足特定的函数模型,有一定局限性[16]。矩方法中的空间矩法、Zernike矩法、正交Fourier-Mellin矩(OFMM)法以及Pseudo-Zernike矩(PZM)法等方法因精度高和抗噪能力好而被广泛应用,但其定位原理是针对理想边缘模型,存在原理性误差,并且计算量普遍较大。此外,上述各种方法的共同缺点是对屋顶状边缘不能有效检测,即不具有良好的通用性[16, 17]。文献[1]也指出不同方法对两种边缘的检测结果存在明显差异,这在很大程度上影响着遥感影像中目标的检测、识别以及精确定位。为提高检测精度、改善对各种边缘的通用性,本文提出一种利用极值梯度的通用亚像素边缘检测算法。
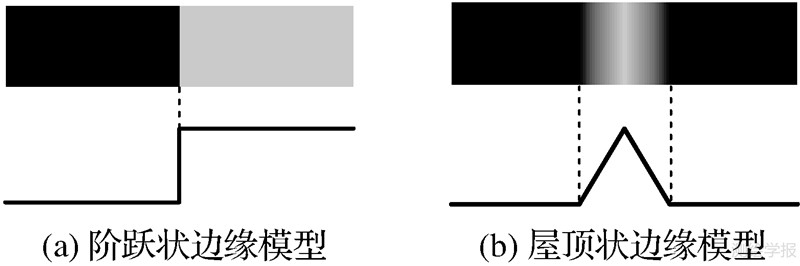
2 边缘初定位的基本原理常见的图像边缘可分为阶跃状边缘和屋顶状边缘两种[18],其理想模型及相应的灰度剖面如图 1所示。
|
| 图 1 两种边缘的理想模型及相应的灰度剖面 Fig. 1 Ideal models and gray section planes of two types of edge |
大部分的典型一阶导数边缘检测算子仅在两个方向上计算边缘强度,且只在灰度变化最大的方向上求解梯度,未考虑到可将梯度细分为灰度增加最大的正梯度和灰度减小最大的负梯度进行处理,并不完全符合实际影像中灰度的分布情况。因此,本方法将梯度分解为灰度增加最大的正梯度和灰度减小最大的负梯度两个部分,并分别进行求解。
极值梯度的大小由当前像点与其8邻域像点之间灰度差值的极值(式(1))所确定,方向为当前像点指向差值极值所对应的邻域像点
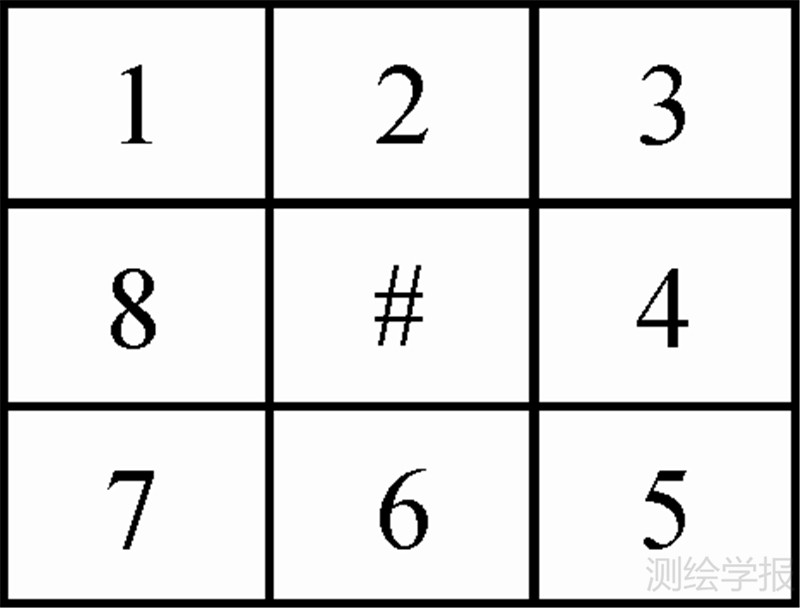
式中,max()、min()分别为最大值函数、最小值函数;gra(i)由式(2)确定,表示当前像点在i号邻域点所在方向上的灰度变化,各邻域点的编号如图 2所示;G1、G2分别表示正梯度和负梯度的大小,实际计算中,用极值对应的邻域点号i表示梯度的方向;i=1,2,…,8 式中,g#、gi分别表示当前像点与i号邻域点的灰度值。
|
| 图 2 当前像点(#)各邻域点的编号示意图 Fig. 2 Number of eight neighborhood points of current pixel(#) |
通过分析gra(i)的特点,发现当其出现全为负数(正数)的情况时,式(1)并不能有效求得正梯度(负梯度)的大小,因此对式(1)进行改进,利用式(3)代替式(1)作为正梯度和负梯度的定义式
式中,各函数和变量的含义同式(1)。需要说明的是,一般通过式(3)求得的梯度大小为正数。根据上述原理可得,每个像点对应两个梯度向量,与典型一阶导数边缘算子同理,梯度的大小代表了该像点的“边缘强度”,为确定初始边缘,本方法分别对两个梯度采用阈值化处理和局部非极大抑制处理。在进行阈值化处理时,“边缘强度”大于设定阈值的边缘点被保留,反之则视为弱边缘或者非边缘点而被剔除,阈值的设定与影像本身所含特征量及所提取边缘的应用目的有关。局部非极大抑制实质上是仅保留在梯度方向上灰度变化最剧烈的像点,具体方法与Canny算子[19]类似。
经过上述两步处理,得到由局部灰度增加最大和减小最大的两类像点共同组成的初始边缘。
2.2 初始边缘的特性分析本小节以阶跃状边缘为例,对利用上文中所得的初始边缘进行亚像素定位的可行性进行分析,并对其所具有的特性进行讨论。
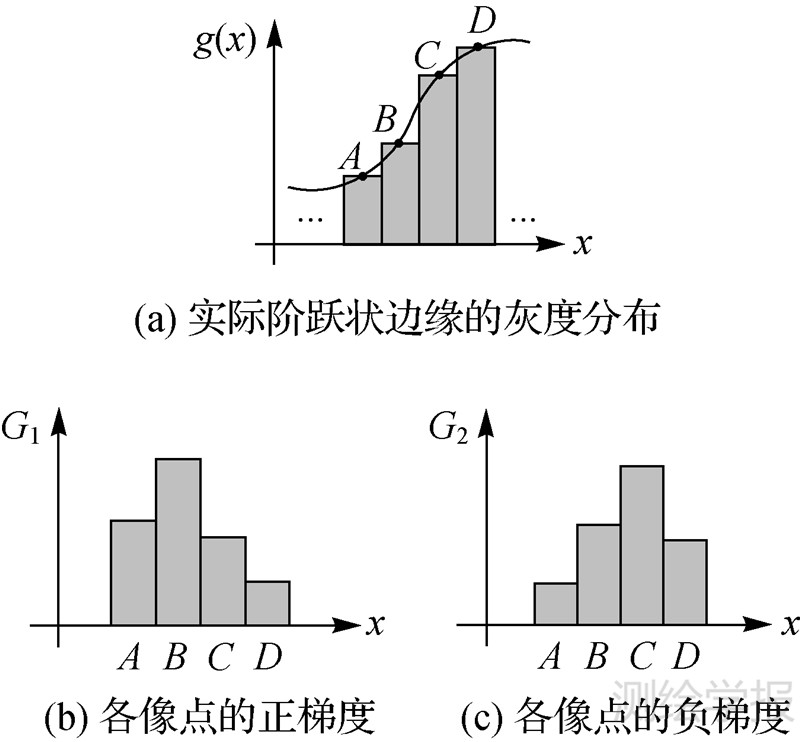
在实际影像中,阶跃状边缘在物方空间剧变的灰度值变成了如图 3(a)所示的渐变形式,A、B、C、D 4点是阶跃状边缘处梯度方向上的4个像点,各像点对应的柱状长度代表灰度值大小,曲线为灰度函数曲线;图 3(b)、(c)分别为各像点的正梯度、负梯度示意图。需说明的是,为便于讨论,此处假设这4个像点的正负梯度在同一直线方向上。
|
| 图 3 实际阶跃状边缘的灰度和梯度 Fig. 3 Gray and gradient of actual step edge |
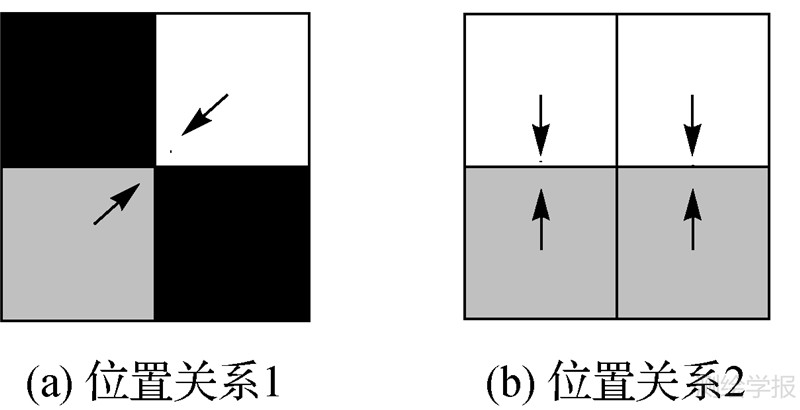
图 3(b)、(c)所示的梯度经过阈值化及局部非极大抑制处理后,仅B点(正梯度局部最大)和C点(负梯度局部最大)被保留,而图 3(a)所示边缘的理论精确位置正是介于B点和C点之间,因此初始边缘与精确边缘的位置关系可由图 4表示(图 4仅仅是两种可能的位置关系)。图中灰色框表示局部灰度增加最大的像点,白色框表示局部灰度减小最大的像点,黑色框表示非边缘点,方框中箭头的方向表示该边缘点的梯度方向,小黑点表示边缘的精确位置。因此,利用由局部灰度增加最大和减小最大的两类像点共同组成的初始边缘进行边缘的亚像素定位具有一定的可行性。
|
| 图 4 初始边缘与精确边缘的两种位置关系示意图 Fig. 4 Two cases of ubiety between initial edge and accurate edge |
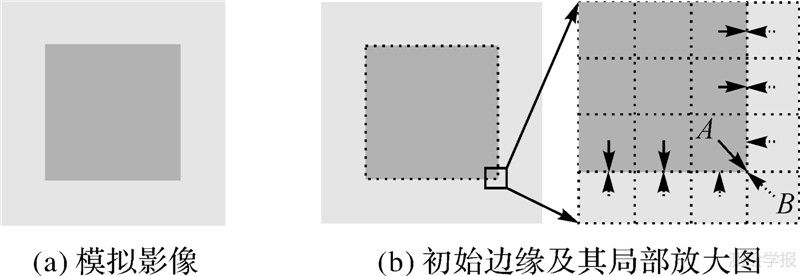
对如图 5(a)所示的模拟影像进行边缘初定位的结果如图 5(b)所示,局部放大图中每一个虚线框表示一个像点,实线箭头和虚线箭头所在像点分别是局部灰度增加最大、减小最大的像点,箭头方向表示对应的梯度方向。由图可知,在非角点边缘处,两类像点一一对应,这种由两种梯度共同确定的边缘,保证了提取结果的可靠性与稳定性;在角点附近,两类像点出现了多对一的情形,因此,不仅可以较好地提取角点,在角点附近还能提取到更密集的边缘点,这更有益于边缘检测的后续工作边缘跟踪的进行。
|
| 图 5 模拟影像及本文方法提取的初始边缘 Fig. 5 Simulative image and initial edge from the proposed algorithm |
通过对极值梯度的求解与处理得到了初始边缘,下面着重分析阶跃状边缘和屋顶状边缘的初始边缘所具有的特点,然后建立各自的亚像素定位拟合模型。
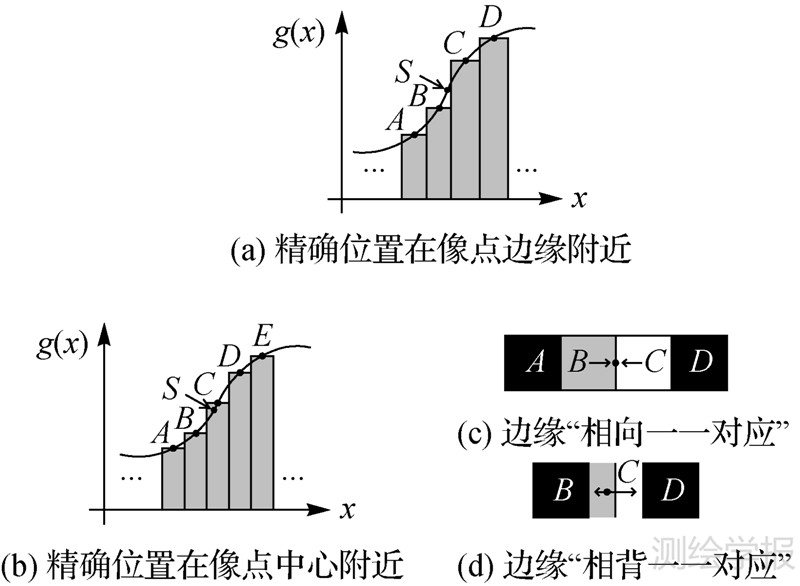
3.1 阶跃状边缘的亚像素定位模型对于阶跃状边缘,根据灰度变化最剧烈处(即边缘精确位置)与各像点中心的位置关系,可细分为如图 6(a)、(b)所示的两种情形。图 6中柱状长度、方框颜色、箭头方向及黑点的含义与图 3(a)、图 4相同,图 6(a)、(b)中x轴上的坐标代表边缘梯度方向上的各像点,图 7、图 8与此同理。
|
| 图 6 阶跃状边缘初始边缘的两种情况 Fig. 6 Two cases of initial edge of step edge |
|
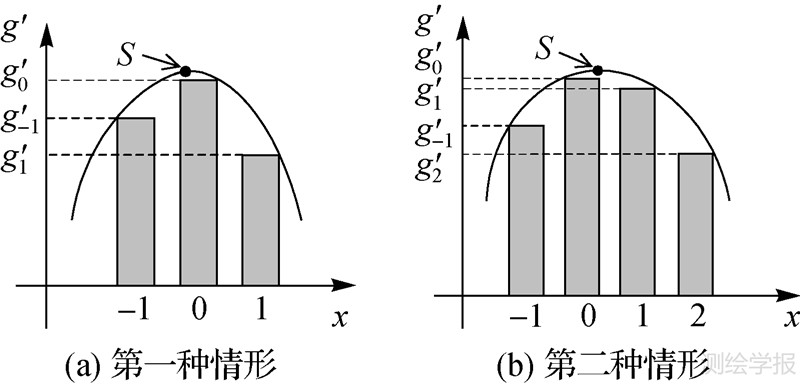
| 图 7 阶跃状边缘的亚像素定位模型 Fig. 7 Sub-pixel edge detection models for step edge |

|
| 图 8 屋顶状边缘的亚像素定位模型 Fig. 8 Sub-pixel edge detection models for roof edge |
图 6(a)代表边缘的精确位置S位于像点边缘附近的情形,其初始边缘如图 6(c)所示,像点B、C分别被检测为局部灰度增加最大、减小最大的像点,即两类像点相向一一对应。
图 6(b)代表边缘的精确位置S位于像点中心附近的情形,由于像点C的正梯度和负梯度均为局部极大值,即同时是局部灰度增加最大和减小最大的像点(如图 6(d)所示)。因此,两类像点相背一一对应。
根据中心极限定理,物方空间灰度剧变的边缘经光学成像后灰度变化应符合高斯分布,曲线顶点为边缘的精确位置。由于二次曲线是高斯曲线的高次逼近,利用二次曲线来近似高斯曲线,不仅误差较小,还可大大提高计算效率。因此,本文利用式(4)所示的二次曲线对阶跃状边缘的梯度函数进行拟合。
对于上述两种情形,边缘精确位置S附近的梯度分布如图 7所示。为解算方便,将像点B、C之间梯度值对应的横坐标置为0,然后利用式(5)和式(6)所示的拟合数据分别对两种情形的模型参数进行求解
式中,G1(·)、G2(·)分别表示对应点的正梯度、负梯度;g′i表示用于拟合梯度函数的梯度值。因此,边缘的精确位置相对于基准像点中心的位移量为
式中,x0为二次曲线的顶点坐标,式中后半部分的“-”、“+”分别在第一种情形和第二种情形中取得。位移方向与位移量的正负有关,当x′0>0时,位移方向为基准像点的正梯度方向;反之,则为负梯度方向。这里的基准像点在两种情形中分别为像点B和像点C。
此处仅对灰度增大时的阶跃状边缘的定位模型进行了讨论,而灰度减小时的阶跃状边缘的定位模型与其同理,不再赘述。
3.2 屋顶状边缘的亚像素定位模型对于屋顶状边缘,边缘的精确位置位于灰度增大和减小的变化处,灰度变化(先增大后减小或者先减小后增大)的整个过程是在较小的空间距离内完成的,因为若平缓区域较宽则变成了一对阶跃状边缘。因此,本方法在讨论屋顶状边缘的定位模型时仅考虑其覆盖的空间距离较小的情形,并利用如式(8)所示的二次曲线模型对屋顶状边缘的灰度曲线进行拟合,曲线顶点即为边缘的精确位置。需要指出的是,这里提到的边缘所覆盖的空间距离指局部灰度增加(或减小)最大的像点在梯度方向上的间距,而不是由图像直观判断得到的边缘宽度。此处仅讨论m<0的情形,即灰度先增大后减小的屋顶状边缘(如图 8(a)所示),而m>0的情形与其同理,不再赘述
图 8(a)是屋顶状边缘附近的灰度分布示意图,曲线是屋顶状边缘处的灰度函数模型,S点是边缘的理论精确位置。图 8(b)、(c)表示屋顶状边缘处初始边缘的两种情形,其中像点A、C均是局部灰度增加最大的像点,且正梯度方向均指向像点B,不同之处在于图 8(b)中像点B不是局部灰度减小最大的像点,但这对边缘的定位没有实质性的影响,边缘的精确位置(小黑点)均应位于像点B中心附近。
在求得初始边缘后,通过对各像点处初始边缘进行分析判断,若符合图 8(b)、(c)所示的情形,即判定为屋顶状边缘,然后利用梯度方向上相邻像点(如此处的像点A、B、C)的灰度值对式(8)所示的灰度模型参数进行求解,边缘的精确位置为
式中,g-1、g0、g1分别表示像点A、B、C的灰度值。此时x0即为边缘精确位置相对于像点B中心的位移量,位移方向与位移量的正负有关,当x0>0时,位移方向为像点C的正梯度方向;反之,则为负梯度方向。
4 算法实现步骤前文对边缘初定位和亚像素定位等关键步骤的相关原理进行了说明,本方法的具体步骤如下:
(1) 利用高斯双边滤波[20]对影像进行保边平滑处理。
(2) 边缘初定位。逐像点求解极值梯度,并分别对两个梯度向量进行阈值化处理和局部非极大抑制处理得到初始边缘。实际计算中,为减小噪声的影响,保证算法的可靠性和稳定性,利用式(2)计算像点在各方向上的灰度变化时,用当前邻域点及其两侧相邻邻域点的灰度均值代替当前邻域点的灰度值,例如用图 2中的1、2、3号邻域点的灰度均值g2'代替g2参与计算。
(3) 边缘的精确定位。由于不同边缘类型的初始边缘具有不同的表现形式,在利用初始边缘进行精确定位时首先需要判断边缘类型,然后再利用相应的定位模型进行精确定位。具体步骤如下:
a. 首先寻找“多对一”的初始边缘,若这多个同种边缘点中存在两个边缘点在同一直线上且梯度方向相对(如图 8(b)、(c)),即边缘“二对一”情形,则将其判定为屋顶状边缘,并按照3.2中的定位模型进行求解;否则,将这多个同种边缘点分别与另一种边缘点组成“相向一一对应”边缘,按照3.1中定位模型的第一种情形进行求解。
b. 然后寻找“相背一一对应”的初始边缘,并将其按照3.1中定位模型的第二种情形进行求解。
c. 最后对“相向一一对应”的初始边缘按照3.1中定位模型的第一种情形进行求解。
(4) 离散边缘点剔除。剔除检测出的离散边缘点和噪声点。
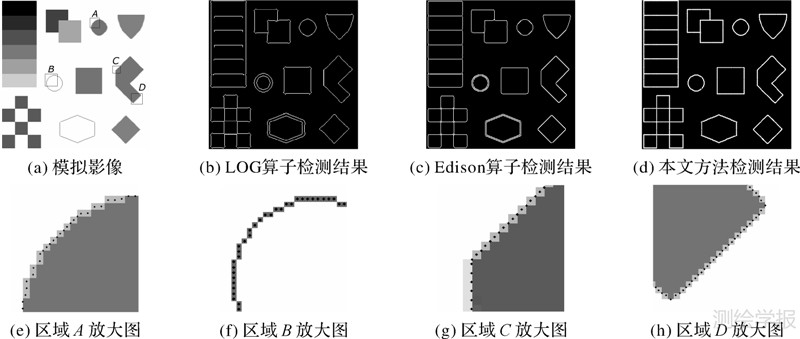
5 试验与结果分析 5.1 试验1 利用模拟影像检验算法的通用性、定位能力LOG算子是高斯滤波和拉普拉斯算子的结合,能有效抑制噪声的影响。Edison算子[21]是Canny算子的改进,通过增加边缘置信度这一指标增强了弱边缘检测能力以及对噪声的抑制效果。下面利用LOG算子、Edison算子以及本文的方法对如图 9(a)所示的模拟影像进行边缘检测,结果如图 9(b)-(d)所示。图 9(a)中A-D 4个区域包含各种边缘:区域A包含曲线状阶跃状边缘、区域B包含曲线状屋顶状边缘、区域C包含倾斜和竖直直线状阶跃状边缘、区域D包含倾斜直线状阶跃状边缘和角点。为了更直观地显示检测结果,将本文方法检测所得的亚像素边缘点投影到原始影像上,上述4个区域检测结果的放大图分别如图 9(e)-(h)所示,图中小黑点为检测所得的亚像素边缘点。
|
| 图 9 模拟影像及3种方法的边缘检测结果 Fig. 9 Simulative image and edge detection results from three detectors |
由试验结果可知,LOG算子和Edison算子仅能检测阶跃状边缘,不能有效地检测屋顶状边缘,其原因是Edison算子在确定边缘置信度时采用阶跃状边缘模型建立标准边缘模板。另外这两种算子对角点及多条边缘的交点不能较好地提取,还可能出现漏检的情况。而本文方法对不同的边缘类型都能较好地识别与检测,具有良好的通用性,并且对角点以及边缘的交点也能有效地提取,能较好地保持目标的形状。
5.2 试验2 利用标准边缘影像定量评价算法的定位能力文献[22]以CCD成像原理为基础,根据方形孔径采样定理,给出了生成理想直线型阶跃边缘的方法。考虑到实际成像时光学成像系统对图像的平滑作用,本文以文献[22]的理想边缘经过平滑处理所得结果作为试验用的标准阶跃状边缘。在Intel 2.93 GHz、2GRAM和Matlab R2012a的软硬件环境下,利用大小为201像素×201像素、倾斜角为0°至45°且以5°为间隔的一组标准阶跃状边缘影像比较几种典型的亚像素检测算子以及本方法的定位能力。各方法的定位精度(如表 1所示)是利用其对不同倾斜角的边缘的定位精度的平均值来衡量,而对某倾斜角边缘的定位精度则是所检测的各边缘点与理论边缘直线的距离平均值。
下面比较各方法对屋顶状边缘的定位精度。此处用于试验的标准屋顶状边缘是对水平直线型的理想屋顶状边缘按一定角度进行旋转,再经过平滑处理所得,图 10(a)所示为倾斜角为40°的标准边缘。

|
| 图 10 标准屋顶状边缘及各算法的检测结果 Fig. 10 Standard roof edge and edge detection results from different algorithms |
Edison算子、OFMM法及本文方法对如图 10(a)所示的标准屋顶状边缘的检测结果分别如图 10(b)-(d)所示,图中小白(黑)点为检测边缘点的精确位置。由结果可知,Edison算子和OFMM法在检测屋顶状边缘时会在真实边缘两侧分别检测出一条边缘,即无法对其进行有效检测,不具有通用性。显然,讨论这些非通用算法对屋顶状边缘的定位精度无实际意义,故后文仅比较通用算法对屋顶状边缘的定位精度。
利用本文方法与基于质心的方法[16]对上述标准屋顶状边缘进行检测,对比试验结果见表 2。
| 基于质心的方法 | 本文方法 | |
| 定位精度/像素 | 0.292 | 0.147 |
| 检测时间/ms | 39 | 85 |
从表 1、表 2及图 10可知,插值法计算时间短、精度最低;拟合法和几种矩方法计算效率较低,精度相对插值法有较大提高,特别是OFMM法和PZM法的定位精度很高,达到了0.1像素,但它们均不能对屋顶状边缘进行有效检测。基于质心的方法计算效率高,对两种标准边缘都能有效检测,对阶跃状边缘有较高的定位精度。相比而言,本文方法检测时间稍长,但对两种边缘的检测性能更稳定,有更高的定位精度。综合比较可得,本方法通用性好,边缘定位精度高,并且精度与效率达到了一个较好的平衡。
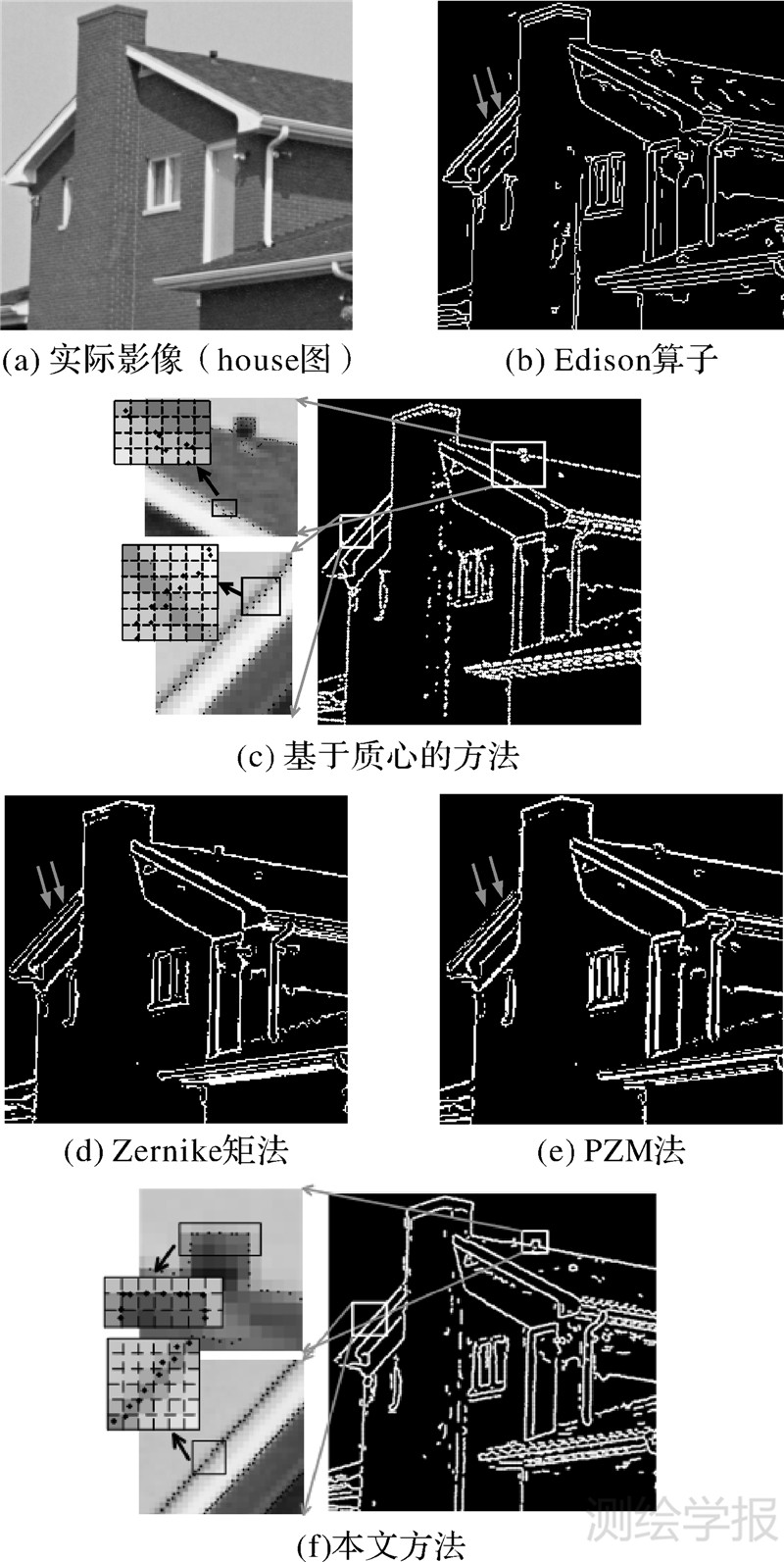
5.3 试验3 利用实际影像验证算法各方面的性能为进一步验证本算法各方面的性能,利用图 11(a)所示的影像进行对比试验。图 11(b)-(f)分别为Edison算子、基于质心的方法、Zernike矩法、PZM法以及本文方法的检测结果,其中图 11(c)、(f)进行了两次局部放大,黑点为检测所得的边缘点,第二次放大图中每一个虚线框表示一个像素。
|
| 图 11 实际影像及其边缘检测结果 Fig. 11 Real image and edge detection results |
由试验结果可知,Edison算子有较好的弱边缘检测性能,所得边缘连续性较好,但也会因此检测出一些非边缘点,如图 11(b)中屋顶位置处的一些虚假边缘;Zernike矩法和PZM法抗噪能力强,但其边缘响应较宽,弱边缘检测能力较差,仅能检测到强边缘。此外,上述3种方法在检测屋顶状边缘时都会检测出两条边缘,如图 11(b)、(d)、(e)中灰色箭头所指的两条边缘。基于质心的方法对各种边缘均有效,但却出现了部分像素内有多个边缘点,而部分像素内无边缘点的情况(如图 11(c)所示),这造成了边缘连续性较差,这是由于其在对初始边缘点进行平移改正时未考虑边缘方向等因素,这也使得其改正量很容易受噪声的影响,因此尽管该方法能达到亚像素级定位精度,但仅适用于简单边缘的检测。本文方法对屋顶状边缘的检测结果优于基于质心的方法,并且在角点处能得到相对较密集的边缘点(如图 11(f)左上方的放大图所示),这不仅有助于提取角点,还对下一步边缘跟踪有重要意义,此外本文方法能检测出图中墙体上的大部分弱边缘,并且虚假边缘较少,这是由于所提取的每一个边缘点均由两种边缘点共同确定,有较强的可靠性,这也在一定程度上降低了噪声的影响。因此,本文方法有较好的可靠性和通用性,对各种边缘以及角点均有较高的定位精度,并对噪声有一定的抑制作用。
6 结 论边缘检测在遥感影像分割、目标识别以及地物提取等影像分析处理中起着重要的作用。本文针对传统方法通用性和精度需进一步提高等问题,提出一种利用极值梯度的通用亚像素边缘检测算法。为了更符合梯度的实际分布情况,本算法首先将梯度分解为正梯度和负梯度并分别进行求解,在经过阈值化和局部非极大抑制处理后得到由两种边缘点共同构成的初始边缘。对亚像素定位的可行性进行分析之后,针对不同边缘类型的初始边缘所具有的特点,分别建立了阶跃状边缘和屋顶状边缘的亚像素定位拟合模型。由于本方法最终检测所得的边缘由两种边缘点共同确定,结果具有较好的可靠性和稳定性,几组对比试验的结果验证了本方法对不同类型边缘都能较好地提取,通用性较好,对包括角点在内的边缘均有较高的定位精度,并且对噪声有一定的抑制作用。
在后续研究中,将着重进行边缘跟踪的相关研究,并利用不能与另一类边缘像点组合的某一类边缘像点对边缘进行补充,以解决部分边缘存在断裂的问题,实现影像分割和地物的高精度自动提取。另外,如何提高本方法对弱边缘的检测性能以及强噪声干扰下的稳定性也值得进一步研究。
| [1] | ZHAO Xi’an, LI Deren. Constructing Two Dimension Symmetric Wavelets for Extracting Edge Features of Image at Multiscales[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 313-319. (赵西安, 李德仁. 二维对称小波与多尺度影像边缘特征提取[J]. 测绘学报, 2003, 32(4): 313-319.) |
| [2] | WANG Ke, XIAO Pengfeng, FENG Xuezhi, et al. The Modified Algorithm of Image Edge Features Detection Based on 2D Discrete Hilbert Transform[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. (王珂, 肖鹏峰, 冯学智, 等. 基于改进二维离散希尔伯特变换的图像边缘检测方法[J]. 测绘学报, 2012, 41(3): 421-427.) |
| [3] | WU Guiping, XIAO Pengfeng, FENG Xuezhi, et al. A Method of Edge Feature Detection from High-resolution Remote Sensing Images Based on Frequency Spectrum Zone Energy[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 587-591. (吴桂平, 肖鹏峰, 冯学智, 等. 一种基于频谱段能量的高分辨率遥感图像边缘特征检测方法[J]. 测绘学报, 2011, 40(5): 587-591.) |
| [4] | MEFTAH B, LEZORAY O, BENYETTOU A. Segmentation and Edge Detection Based on Spiking Neural Network Model[J]. Neural Processing Letters, 2010, 32(2): 131-146. |
| [5] | DEMERS M. Edge Detection Using Fractal Imaging[J]. International Journal of Mathematical Modelling and Numerical Optimisation, 2012, 3(4): 266-280. |
| [6] | HUANG C P, WANG R Z. An Integrated Edge Detection Method Using Mathematical Morphology[J]. Pattern Recognition and Image Analysis, 2006, 16(3): 406-412. |
| [7] | HERMOSILLA T, BERMEJO E, BALAGUER A, et,al. Non-linear Fourth-order Image Interpolation for Subpixel Edge Detection and Localization[J]. Image and Vision Computing, 2008, 26(9): 1240-1248. |
| [8] | QU Yufu, PU Zhaobang, WANG Yaai. Contrast Study of Subpixel Edge Detection in Vision Measuring System[J]. Chinese Journal of Scientific Instrument, 2003, 23(3): 460-462. (屈玉福, 浦昭邦, 王亚爱. 视觉检测系统中亚像素边缘检测技术的对比研究[J]. 仪器仪表学报, 2003, 23(3): 460-462.) |
| [9] | LI Zhe, DING Zhenliang, YUAN Feng. Subpixel Algorithm Based on Level Interpolation and Least Squares Fitting[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2008, 32(5): 615-618. (李喆, 丁振良, 袁峰. 基于分层插值和最小二乘拟合的亚像素细分算法[J]. 南京理工大学学报: 自然科学版, 2008, 32(5): 615-618.) |
| [10] | DA F P, ZHANG H. Sub-pixel Edge Detection Based on an Improved Moment[J]. Image and Vision Computing, 2010, 28(12): 1645-1658. |
| [11] | QU Y D, CUI C S, CHEN S B, et al. A Fast Subpixel Edge Detection Method Using Sobel-Zernike Moments Operator[J]. Image and Vision Computing, 2005, 23(1): 11-17. |
| [12] | GAO Shiyi, ZHAO Mingyang, ZHANG Lei. Improved Algorithm about Subpixel Edge Detection of Image Based on Zernike Orthogonal Moments[J]. Acta Automatica Sinica, 2008, 34(9): 1163-1169. (高世一, 赵明扬, 张雷. 基于Zernike正交矩的图像亚像素边缘检测算法改进[J]. 自动化学报, 2008, 34(9): 1163-1169.) |
| [13] | BIN T J, LEI A, CUI J W, et al. Subpixel Edge Location Based on Orthogonal Fourier-Mellin Moments[J]. Image and Vision Computing, 2008, 26(4): 563-569. |
| [14] | ZHANG K, CHEN H Q, LIANG Q W, et al. Subpixel Edge Detection Algorithm Based on Pseudo-Zernike Moments[C]// Proceedings of International Society for Optical Engineering. Dalian: The International Society of Optical Engineering, 2010: 765-771. |
| [15] | YI Mo, LIU Zhongxuan, PENG Silong. Subpixel Edge Location Using Improved LSR[J]. Journal of Image and Graphics, 2005, 10(10): 1314-1319. (易沫, 刘忠轩, 彭思龙. 水平集重构方法改进及亚像素边缘定位[J].中国图象图形学报, 2005, 10(10): 1314-1319.) |
| [16] | LIN Xintang, WANG Zongyi. A Novel Universal and Fast Algorithm for Two-dimensional Subpixel Edge Detection[J]. Applied Science and Technology, 2010, 37(8): 35-39. (林欣堂, 王宗义.一种新的快速通用二维图像亚像素边缘检测算法[J]. a href="http://www.cnki.com.cn/Article/CJFDTOTAL-YYKJ201008010.htm" target=_blank title="点击浏览原文">应用科技, 2010, 37(8): 35-39.<) |
| [17] | SHENG Zunbing, CUI Xianyu, GAO Guo’an. A Universal Algorithm for Subpixel Edge Detection[J]. Journal of Shanghai Jiaotong University, 2007, 41(6): 911-915. (盛遵冰, 崔贤玉, 高国安. 通用亚像素边缘检测算法[J]. 上海交通大学学报, 2007, 41(6): 911-915.) |
| [18] | GENG Zexun, ZHANG Baoming, FAN Dazhao. Digital Photogrammetry[M]. Beijing: Surveying and Mapping Press, 2010. (耿则勋, 张保明, 范大昭. 数字摄影测量学[M]. 北京: 测绘出版社, 2010.) |
| [19] | CANNY J F. A Computational Approach to Edge Detection[J]. IEEE Transactions on PAMI, 1986, 8(6): 679-698. |
| [20] | KUNAL N C, SAGE D, UNSER M. Fast O(1) Bilateral Filtering Using Trigonometric Range Kernels[J]. IEEE Transactions on Image Processing, 2011, 20(12): 3376-3382. |
| [21] | MEER P, GEORGESCU B. Edge Detection with Embedded Confidence[J]. IEEE Transactions on Pattern Analysis and Machine Intellegence, 2001, 23(12): 1351-1365. |
| [22] | HE Zhonghai, WANG Baoguang, LIAO Yibai. Study of Method for Generating Ideal Edges[J]. Optics and Precision Engineering, 2002, 10(1): 89-93. (贺忠海, 王宝光, 廖怡白. 理想边缘产生方法的研究[J]. 光学精密工程, 2002, 10(1): 89-93.) |