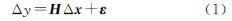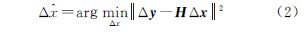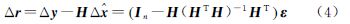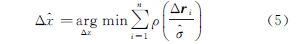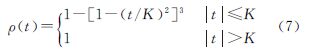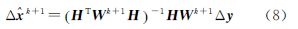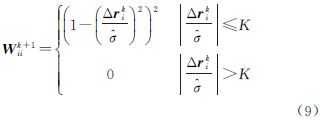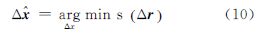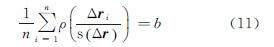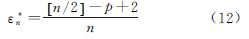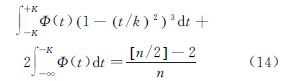1 引 言
随着北斗、伽利略以及GPS现代化的推进,未来的用户机将拥有更多、更精确的伪距观测值。由于可见星的增多,伪距中粗差发生的概率增大,但常用的最小二乘定位结果容易受到粗差的影响。一种简单且成熟的方法是采用RAIM(receiver autonomous integrity monitoring)算法进行粗差的探测和排除。由于RAIM算法设计之初是为了处理GPS应用中可能出现的单个较大的粗差,所以在处理多个粗差以及单个较小的粗差时暴露出诸多不足[1]。同时,以M估计为代表的抗差(稳健)估计[1, 2, 3, 4]在多卫星导航系统组合定位中的应用得到了越来越多的关注。
目前,基于M估计的卫星导航定位算法研究主要集中在两个方面:一方面是针对特定的观测噪声模型,构建合适的目标函数对单历元的观测数据进行处理。当观测噪声互相关时,文献[5, 6]提出了IGGIII算法以及改进后的双因子方法抑制粗差,其采用三段式ρ函数与传统M估计的Huber函数不同。类似的,通过对Danish函数的改进,文献[7]给出了更一般的表达式来应对相关的观测噪声。当观测噪声为理想高斯模型时,经典的Huber函数可有效地抵制单个粗差,基于牛顿迭代的快速计算方法[8]使其工程应用成为可能。当观测噪声为混合模型时,文献[9]提出了一种自适应的抗差估计方法,通过误差统计量的假设检验,自适应调整ρ函数。另一方面充分利用多个历元的观测数据,将M估计应用于时域滤波过程中以提高抗差性,文献[10]解决了抗差估计在卡尔曼滤波应用中的秩亏问题。自适应的抗差卡尔曼滤波[11]不仅能有效抑制粗差,而且适应观测噪声模型的变化,进一步优化了定位结果。
以上两个方面的研究和探讨均以迭代计算的初值没有严重偏离真值为前提条件。当粗差污染较严重且接收机运动状态没有先验信息时,传统的最小二乘初值计算结果作为初值时会含较大的偏差,从而使M估计抗差性受影响[12,13]。通过预测残差的方法[14],虽然可以改善卡尔曼滤波的抗差性,但对用户的动态范围有一定的限制且不适用于单历元的抗粗差定位。通过改进S估计的目标函数,解决了多个粗差引起的初值偏离问题,使得基于M估计的定位算法能够有效抑制多个粗差。
2 传统M估计抗差定位的局限性为减少观测数据的粗差对定位结果的影响,可采用抗差M估计。该估计方法与最小二乘估计不同之处主要是目标函数的选取。下面简单介绍基于M估计的定位原理,然后分析与最小二乘估计的不同之处以及该估计在抗差中的局限性。
GPS定位解算时,初始值x0=[x0y0z0b0]T处线性化的观测方程后,得
式中,Δy是n×1矢量,其元素为各卫星观测伪距与线性化点预测的伪距之差,n是可见卫星数;Δx是n×1矢量,其元素是相对于线性化点的偏差;H是Δx和Δy的关联矩阵,也称观测矩阵;ε是n×1的测量误差矢量,其元素一般假设为相互独立的高斯随机过程。为求解线性方程(1),常见的最小二乘估计的目标函数如下
相应的 伪距残差矢量为当测量噪声为高斯分布时,最小二乘估计为最优估计,但实际观测量中常常含有粗差,由式(2)和式(4)可知,粗差会直接影响定位结果,从而使得观测矩阵H偏离真值,导致粗差向伪距残差投影时产生偏差。因此,采用最小二乘准则解算后,伪距残差的大小不能正确反映粗差的大小,整个定位结果会受粗差影响而远远偏离真值。
对于M估计,式(2)可用如下形式表示
式中,函数ρ(·)为一阶可导的偶函数,由M估计根据具体情况可设计不同的加权函数;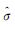 是Δy方差的估计值,通常由下式计算[9]
式中,med(·)表示取向量元素的中值。
是Δy方差的估计值,通常由下式计算[9]
式中,med(·)表示取向量元素的中值。
M估计主要通过选择合适的函数ρ,自动为含粗差观测值分配小的加权值,从而达到抑制粗差的目的。根据观测噪声模型的不同,国内外学者对多种有效的ρ函数进行了深入的研究[15,16]。从抑制幅值较大的粗差方面考虑,本文采用文献[16]中的双边加权函数
式中,K是根据M估计方差性能确定的常数。此时,M估计结果的迭代式如下 式中,Wk+1称为等价权矩阵,满足 式中,Wiik+1和Δrik的上标均为迭代次数,在实际计算过程中,为避免加权引起秩亏,上式中0常以较小的实数代替。由于式(3)和式(8)相似的特点,M估计又可看做是选择权迭代最小二乘估计。文中称该估计为传统M估计,其计算流程总结如下:(1) 采用最小二乘计算结果作为初值。
(2) 根据式(4)计算伪距残差矢量并估计方差,再由式(9)得到等价权矩阵。
(3) 由M估计的迭代式(8)计算第k+1次估计结果,其中k=0,1,2,…。
(4) 返回步骤 (2),直到max|xk+1-xk|小于门限值。
由上述计算流程可知,传统基于M估计的抗差前提条件是初值不能偏离真值太远。由于伪距观测值与用户位置、钟差之间是非线性关系,而H矩阵是观测方程在初值点展开的雅可比矩阵。当粗差的幅值较大时,最小二乘估计结果会出现远远偏离真值的情况,此时矩阵H不再是伪距和用户位置线性关系的有效近似。受到卫星几何结构的影响,每个伪距测量值精度对定位结果的影响各不相同。当粗差存在于影响最大的伪距上时,定位结果会产生明显偏移,这种情况的定量分析可参考接收机自主完好性算法。由此可见,当初值远远偏离真值时,伪距残差不能有效反映伪距测量精度,那么基于伪距残差加权的抗差M估计性能将会受到严重影响。
3 改进后的M估计定位解算方法由前一节的分析可知,用户位置和钟差的初值误差会直接影响到抗差定位的性能。当可用的观测数据量趋于无穷大时,文献[17]给出了一种抗差估计方法即S估计,该估计方法能有效抑制多个粗差。S估计的目标函数如下
式中,s(Δr)满足 式中,0≤b≤1且b=EΦρ(t),Φ是标准正态分布函数。在样本数趋于无穷多时,b通常取0.5,相应的双边加权函数ρ(t)中的K=1.547,而此时S估计的效率约为0.287。可见S估计抗差性能的提高是以方差增大为代价的。本文将利用S估计的这个特点,把其估计结果作为M估计迭代开始的初值,从而进一步提高定位结果的精度和可靠性。
GPS用户通常可见卫星数为7~12颗。当伪距观测值数量有限时,S估计的抗差性能会有所下降[18],崩溃点(breakdown point,BP)描述了该估计所能容忍的含粗差样本比例上限[19]。样本数为n时,S估计的BP可通过式(12)计算
式中,符号[·]表示取整数;p为待估参数的数量。在本文中,n表示可用的卫星数,待估参数为接收机的X、Y、Z坐标和钟差,即p=4。当含粗差观测值的数量增多到满足式(12)时,S估计的抗差性将无法保证。那么S估计用于定位初值解算时最多能抑制的粗差数m满足 由式(13)可知,当n=10时,m=2;当n=12时,m=3。即10颗卫星可用时最多能有效抑制2个粗差,12颗卫星可用时最多能有效抑制3个粗差。随着可用卫星数的增多,抗差性能也不断增强。直接将S估计用于求解方程(1)得到定位结果不是高斯噪声下的最优估计,且定位精度下降明显。比较式(11)和式(12),发现有限个观测值无法达到接近0.5抗差极限,而此时双边加权函数的K仍取1.547不仅不能得到预期的抗差性能,而且使得估计结果方差过大。为了让估计值的方差减小,同时不影响S估计的抗差性能,令b=εn*,展开后得到
式中,n为可见卫星数;K为待确定的参数。通过数值计算方法,得到K与n的对应关系如表 1所示。| n | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| K | 2.937 | 3.189 | 2.561 | 2.756 | 2.349 | 2.510 | 2.212 |
在利用S估计计算初值前,将加权函数中的系数K根据可用观测伪距的数量进行合理选择,避免由于固定K引起的发散,从而在不降低抗差性能的前提下提高估计效率。
综合以上分析,基于改进后M估计的定位解算流程可总结:首先,根据可用卫星数n查表选择K;其次,结合所选K,联立式(7)、式(10)和式(11)求解抗差初值;最后,以抗差初值代替迭代最小二乘法得到的初值进行M估计的定位解算,基于M估计的迭代过程见上一节流程步骤(2)—步骤(4)。通过M估计的迭代计算将进一步减小估计结果的方差,提高定位精度。
4 实测GPS数据处理结果分析GPS实测数据采用美国联邦航空局提供的参考站观测数据,文件为“Acv_EPak_1330_1616_06”,其观测值更新频率为1次/s,持续时间为1h,可见卫星数为10~12颗,图 2(c)中给出了可见卫星数随时间的变化情况。采用斯坦福大学开发的Matlab工具包SGMP[20]进行LS定位解算。目前,该工具包仅提供最小二乘的定位解算,将基于Huber函数的M估计[8]和本文改进后的抗差估计分别替换RAIM得到传统的M估计和本文改进后的M估计定位结果。为比较3种定位算法的抗差性,设计了4个场景:一是不含粗差,即粗差为0;二是指定PRN3卫星含粗差且粗差随时间增大,最大幅值为300m;三是指定PRN3和PRN6两颗卫星含粗差,两个粗差随机生成且互不相关,服从0到300的均匀分布;四是指定PRN3、PRN6和PRN9共3颗卫星同时含有粗差且3个粗差之间相互独立,服从场景三中的均匀分布。

|
| 图 2 改进后的M估计 Fig. 2 The modified M-estimate |
将RAIM、传统M估计和改进后的M估计3种抗差定位算法分别对粗差污染程度不同的4种场景数据进行处理。3种定位算法在不同场景下的三维位置(地心地固系)的定位精度比较详见表 2。从表中可以看出,在无粗差情况下,3种定位解算结果一致;改进前后的M估计结果与RAIM相比,Z轴方向精度均略有下降。随着粗差个数的增加,RAIM算法定位误差明显增大。传统M估计可有效抵制一个粗差,由于较小的粗差的存在,RAIM算法抑制粗差的性能受到了影响,定位精度有所下降。当两个粗差出现时,RAIM算法的定位精度明显下降,传统M估计的Z轴方向方差明显增大。与前两种算法相比,无论是在单个还是多个粗差情况下改进后的M估计表现出更强的抗差性。
| 粗差 个数 | RAIM | 传统M估计 | 改进后的M估计 | ||||||||
| σx | σy | σz | σx | σy | σz | σx | σy | σz | |||
| 0 | 0.964 | 0.650 | 0.979 | 0.867 | 0.660 | 1.266 | 0.827 | 0.623 | 1.393 | ||
| 1 | 2.713 | 3.032 | 3.975 | 0.895 | 0.669 | 1.529 | 0.926 | 0.656 | 1.566 | ||
| 2 | 9.381 | 12.107 | 10.862 | 13.609 | 8.032 | 61.048 | 0.882 | 0.627 | 1.299 | ||
| 3 | 30.532 | 28.460 | 46.037 | 26.612 | 13.742 | 59.683 | 3.433 | 1.253 | 9.359 | ||
为了进一步验证初值误差对抗差性能的影响,将初值相对于真值的误差进行了统计。表 3给出了M估计算法改进前和改进后初值的三维误差。从表 3中可以看出,传统M估计的初值容易受到粗差影响,随着粗差个数增多,初值偏差显著增大;而改进后的M估计初值具有稳定的粗差抑制性能,受粗差数量变化影响较小。
| m | ||||
| 粗差数 | 0 | 1 | 2 | 3 |
| 改进前 | 1.520 | 25.599 | 80.051 | 142509.131 |
| 改进后 | 26.294 | 26.273 | 25.847 | 46.553 |
图 1和图 2分别给出了传统M估计和改进后M估计两种算法在不同粗差个数下定位误差随时间变化的趋势,其中定位精度用球误差概率来衡量,图示中的SEP95表示95%的球误差概率,即以真值为圆心,SEP95为半径的圆球,估算的三维位置误差落在球内的概率是95%。在图 1中,传统M估计的定位精度随着粗差个数的增加而急剧恶化。相比之下,图 2中定位结果具有很强的抗差性。同时,在图 2(c)中出现了一段时间内定位精度较差的情况,这是因为该时间段历元数据中可用卫星数小于12,卫星数的减少使得改进的M估计算法无法有效抑制3个粗差。

|
| 图 1 传统M估计 Fig. 1 The traditional M-estimate |
结合以上数据处理结果,分析总结如下:
(1) 无粗差时,3种算法的定位精度相差不大,由于M估计是次优估计,所以传统的和改进后的M估计的位置误差都略大于带RAIM功能LS算法。两种M估计均以精度的略微下降来换取抗差性能的提高。
(2) 当有1颗卫星含粗差时,传统的和改进后的M估计的定位精度基本不受粗差影响。当粗差污染严重增至两颗卫星时,带RAIM功能的定位精度变差;传统M估计在少部分历元上抑制了粗差,但是产生100m以上偏差的概率明显增加,定位精度无法满足需要;改进后的M估计有效地抵制了两个粗差,最大三维定位偏差仍在10m以内,且精度与0和1个粗差时基本一致。
(3) 随着可见卫星数的增多,改进后的M估计抗差性能增强。在含3个粗差的图 2(c)中,当卫星数为12时,三维定位偏差在5m以下;当卫星数较少为11时,定位误差达20m左右,当卫星数较少到10颗时,定位误差将近300m。同时该结果也初步验证了式(13)的准确性:从式(13)可知当卫星数大于等于12颗时,改进后的M估计才能有效抑制3个粗差。
4 结 论在高斯噪声假设下,基于LS的定位解算是近似最优的定位算法,但是容易受到粗差的影响。传统RAIM算法和M估计无法有效抵制多个粗差,改进后的抗差定位算法提高了M估计的抗差性能,实现了多个粗差的抑制,并且给出了可见卫星数与所能抑制粗差数之间的关系。GPS数据处理结果验证了该方法的有效性。如何检验粗差个数未超出上限以及提供类似RAIM的保护水平值得进一步深入研究。
| [1] | WANG J L, WANG J. Mitigating the Effect of Multiple Outliers on GNSS Navigation with M-Estimation Schemes[C] //International Global Navigation Satellite Systems Society Symposium. Sydney: Menary Pty Limited, 2007: 1-9. |
| [2] | ANDERSEN R. Modern Methods for Robust Regression [M]. London: Corwin Press, 2008: 48-70. |
| [3] | HUBER P J, RONCHETTI E M. Robust Statistics[M].2nd ed, Hoboken: John Wiley & Sons Inc, 2009:125-144. |
| [4] | KHODABANDEH A, AMIRI-SIMKOOEI A R. GPS Position Time-series Analysis Based on Asymptotic Normality of M-estimation [J]. Journal of Geodesy, 2012, 86(1):15-33. |
| [5] | YANG Y. Robust Estimation for Dependent Observations [J]. Manuscripta Geodaetica, 1994, 19(1): 10-17. |
| [6] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights [J]. Journal of Geodesy, 2002, 76(6-7): 353-358. |
| [7] | WIESER A, FRITZ B K. Short Static GPS Sessions: Robust Estimation Results [J]. GPS Solutions, 2002, 5(3): 70-79. |
| [8] | CHANG X W, GUO Y. Huber's M-estimation in Relative GPS Positioning: Computational Aspects [J]. Journal of Geodesy, 2005, 79(6-7): 351-362. |
| [9] | YANG Yuanxi. Adaptively Robust Least Squares Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 206-211. (杨元喜. 自适应抗差最小二乘估计[J]. 测绘学报, 1996, 25(3): 206-211.) |
| [10] | KOCH K R, YANG Yuanxi. Robust Kalman Filter for Rank Deficient Observation Models [J]. Journal of Geodesy, 1998, 72(7-8): 436-441. |
| [11] | YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning [J]. Journal of Geodesy, 2001, 75(2-3): 109-116. |
| [12] | CROUX C, DHAENE G. Robust Standard Errors for Robust Estimators [J]. CES-Discussion Paper Series (DPS), 2004, 16(3): 1-20. |
| [13] | TONG H, ZHANG G, OU G. Iterative Reweighted Recursive Least Squares for Robust Positioning[J]. Electronics Letters, 2012, 48(13): 789-791. |
| [14] | CHEN Mingjian, ZHOU Fengqi ,HAO Jinming. Improved Robust Filtering Based on Residuals in Real Time Single Point Positioning [J]. Journal of Chinese Inertial Technology, 2009, 17(6): 692-696. (陈明剑, 周凤岐, 郝金明. 在实时单点定位中基于残差信息的改进抗差滤波方法[J]. 中国惯性技术学报, 2009, 17(6): 692-696.) |
| [15] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory [M]. Wuhan: Wuhan University Press, 2002.(李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002.) |
| [16] | KNIGHT N L, WANG J. A Comparison of Outlier Detection Procedures and Robust Estimation Methods in GPS Positioning [J]. The Journal of Navigation, 2009, 62(4): 699-709. |
| [17] | SALIBIAN M, YOHAI V J. A Fast Algorithm for S-Regression Estimates [J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 414-427. |
| [18] | BERRENDERO J R, MENDES B M. On the Maximum Bias Functions of MM-estimates and Constrained M-estimates of Regression [J]. The Annals of Statistics, 2007, 35(1): 13-40. |
| [19] | MARONNA R A. Robust Statistics Theory and Method [M]. Singapore: John Wiley & Sons, 2006: 58-62. |
| [20] | DO Juyong. Stanford GPS/GNSS Matlab Platform [EB/OL]. [2013-01-08]. http://waas. stanford.edu/sgmp/sgmp.html. |