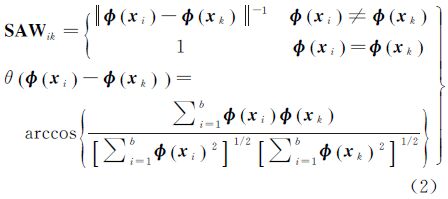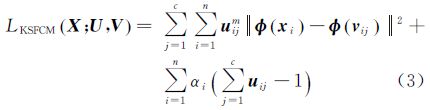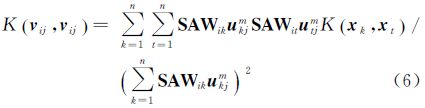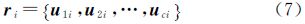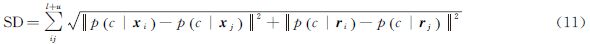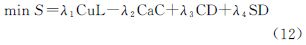1 引 言
许多应用中高光谱遥感影像分类器的设计都是利用类标签的训练样本训练得到,即监督学习。但是对于高光谱遥感影像分类,由于类标签样本少、获取困难,少量的类标签样本很难准确地反映样本点的空间分布特征,导致传统的监督学习算法很难取得较好的分类效果。半监督学习可以利用大量无类标签的样本信息,将少量类标签的样本和大量无类标签的样本相结合提高学习的泛化能力,从而提高分类的准确率。常用的半监督高光谱影像分类方法主要有基于图模型[1, 2]、马尔可夫随机场和稀疏多项式回归[3]、主动学习[4]、判别学习[5]、神经网络[6]、最大期望算法[7, 8]等。而基于核的方法已经被证明是处理高光谱影像的有效工具[9, 10]。支持向量机(support vector machine,SVM)是建立在VC维和结构风险最小化(structural risk minimization,SRM)原理上的基于统计学习理论的机器学习方法。它将模式向量从低维特征空间映射到高维特征空间,在高维特征空间中构造最优分类超平面,用于高光谱影像分类可以取得较好的分类效果[11, 12]。因此半监督SVM应用到高光谱影像分类中能够较好地解决小样本、高维数据的非线性分类问题,具有很好的泛化能力[13, 14, 15, 16, 17, 18]。但是这些半监督方法只是根据分类模型或者分类函数预测类标签未知的对象,并没有从聚类数据结构的角度探索高光谱影像分类。
聚类算法使属于同一聚类的样本相似度最大,属于不同聚类的样本相似度最小,能够很好地反映样本的分布特点,揭示数据结构特征。因此聚类算法也逐渐应用到高光谱影像分类中[19, 20],并表现出一定的优势。本文针对高光谱影像分类提出一种聚类特征和SVM组合的高光谱影像半监督协同分类新方法。该方法利用聚类特征将聚类和分类相结合,达到优势互补,从聚类结构的角度提高分类准确率,降低误分率。
2 基于KSFCM的聚类特征由于高光谱影像光谱分辨率高,不同波段鉴别地物类别的能力具有差异性。为了充分利用各个波段对不同地物的分类能力,本文提出基于光谱角加权模糊核c-均值聚类(kernel-spectral fuzzy c-means,KSFCM)算法。该方法是在基于核函数的模糊c均值聚类(fuzzy kernel c-means,FKCM)[21]算法上进行改进,引入了光谱角权值(spectrally angle weighted,SAW),得到更精确的高光谱影像聚类结果。
FKCM将模式空间的样本非线性映射到高维特征空间,以增加类别之间的可分性,使非线性映射后的样本在高维特征空间达到线性聚类的目的。但是FKCM算法在计算聚类中心时,仅使用了各样本对聚类中心的隶属度,忽略了样本之间固有存在的光谱特征信息。而KSFCM聚类算法在计算模糊核聚类中心时,能够根据SAW使得每个核聚类中心随着样本的光谱信息不同而各有不同。
假定高光谱影像某一样本xi属于某一类别j,j∈1,2,…,c,c为类别数。每一个高维特征空间样本为Φ(xi),i=1,2,…,n,计算不同的模糊核聚类中心Φ(vij)时,根据与Φ(xi)之间的SAW可以得到样本Φ(xi)对类别j的核聚类中心
式中,u为隶属度矩阵;m为聚类的模糊度;权值SAW为 式中,b为波段数;Φ(xk)为初始聚类中心;θ∈[0,π/2]。SAW利用光谱角角度大小决定权值大小。光谱角判断样本光谱与聚类中心光谱之间的近似程度。SAW充分利用了光谱维的信息,强调了光谱的形状特征,夹角越小相似度越大,则权值SAW越大。光谱角度量考虑光谱形状特征,可以在一定程度上消除高光谱影像分类过程中光照、地形等因素的影响,因此SAW能充分利用样本的光谱信息,即光谱夹角θ小的样本应属于此聚类中心类别。定义KSFCM拉格朗日函数
其最小化式LKSFCM的隶属度函数为 式中 样本xi的聚类特征ri,即表示样本xi对每一个聚类中心的隶属度 式中,c为聚类数。聚类特征是从聚类的角度描述数据内在结构特征,用以建立聚类与分类之间的连接,从而使聚类和分类达到优势互补。ri是样本xi对每一聚类的隶属度矢量,因此,满足eTri=1,i∈{1,2,…,N},e为单位列向量。 3 聚类特征和SVM组合的高光谱影像半监督协同分类本文主要思想是建立两个SVM分类器,一个是对原始数据进行SVM半监督分类,另一个是对聚类特征进行SVM分类。由于类别信息一致,两个分类器之间的差异应最小化,因此可以通过对两个分类器建立一定的约束条件求解使得目标函数达到极值的最优分类。本文提出了聚类损耗函数(ClusterLoss,CuL)、分类一致函数(ClassConsistent,CaC)、分类差异性(classification difference,CD)、样本差异性(sample difference,SD)构建协同分类框架,将聚类与分类相结合,充分利用大量无类标签和少量类标签样本信息,实现半监督高光谱影像分类。
高光谱样本X={x1,x2,…,xN},x1={x11,x12,…,x1p},p为波段数。类标签为Y={y1,y2,…,yN},N为样本数。对于类标签有yi∈Y,yi∈{1,2,…,C},其中C为类别数。K是聚类数,在KSFCM算法中定义第K类的聚类中心为vk。矩阵V={v1,v2,…,vK}包含了所有的聚类中心。
3.1 聚类损耗函数聚类损耗函数CuL主要用于判断聚类损失,CuL值越小,聚类结果越好
式中,l表示类标签样本数;u表示无类标签样本数。由于隶属度矩阵是每个样本对聚类中心的隶属度表示,因此聚类损耗函数可以根据样本对每一个聚类中心的隶属度,得到使聚类损失最小的聚类中心。传统的利用聚类算法进行高光谱影像分类往往将隶属矩阵中每一样本隶属度最大的聚类类别赋予此样本,因此可能造成误分,而聚类损耗函数则可以避免该问题,减少样本误分率。 3.2 分类一致函数分类一致函数CaC主要用于判断分类器的分类损失,CaCO表示对原数据进行分类的分类器一致性,CaCC表示对聚类特征进行分类的分类器一致性
分类一致函数是根据概率统计,利用已有的类标签信息,判断SVM分类器分别对原始数据和聚类特征分类的结果与原始类标签的一致性。CaC值越大,表明分类结果与类标签一致性越大,分类效果越好。分类一致函数可以用于约束分类误差样本,使得误差率最小化。
3.3 分类差异性分类差异性CD用于判断两个分类器分类结果的差异。由于类别信息一定,两个分类器之间CD值越小,分类效果越好。本文采用Kullback-Leibler散度计算CD
式中,c={1,2,…,C}。两个分类器的目标分类结果应保持一致,因此,其差异性约束条件能够降低误分率,保证分类结果正确率最大化。 3.4 样本差异性样本差异性SD用于判断类别内样本差异大小。同一类别的两个样本SD值越小,分类效果越好。SD采用欧氏距离计算
由类别准则可知样本类内差异性越小,则样本间的相似程度越大,分类效果越好。
3.5 协同分类框架本文提出的半监督协同分类新方法将聚类与分类结合,使聚类过程有类别信息的指导,而分类过程也可以依据聚类得到的数据内部结构,即聚类特征。协同分类框架建立两个分类器,并根据聚类损耗函数、分类一致函数、分类差异性、样本差异性使目标函数最小化,从而得到最佳分类结果
式中,λ1、λ2、λ3、λ4表示各个约束因子的权重,λ1+λ2+λ3+λ4=1,本文设置λ1=λ2=λ3=λ4=0.25。求解目标函数S最小值,保证聚类损耗最小、分类一致性最高、分类差异性最小、样本差异性最小,从而得到最佳分类结果。其中,聚类损耗函数是对KSFCM的约束,保证聚类算法得到的聚类特征能够最大限度代表高光谱数据内部结构;分类一致性是利用类标签样本进行两个分类器的分类结果验证;分类差异性是对两个分类器结果进行限制,减少样本的误分率;样本差异性函数则是对此算法的一个评价因子,作为判断算法分类效果的评价指数。其中使用SVM对原始数据进行半监督分类步骤为:
(1) 设有样本集X={Xl,Xu},其中,Xl为类标签样本集,Xu为无类标签样本集,输入类标签样本集Xl,无类标签样本集Xu。
(2) SVM对Xl训练,得到分类器C1、C2,其中,C1的参数为默认值,C2的参数为遗传算法优选的参数。
(3) 利用分类器C1对Xu进行预测,并得到标记结果p1。
(4) 利用分类器C2对Xu进行预测,并得到标记结果p2。
(5) 比较p1、p2,选择置信度高的无标签样本及其预测标签加入到训练集中,即将标记结果一致的样本加入到训练集Xl中,并更新Xl。
(6) 返回步骤(2),若满足迭代终止条件,则退出循环。
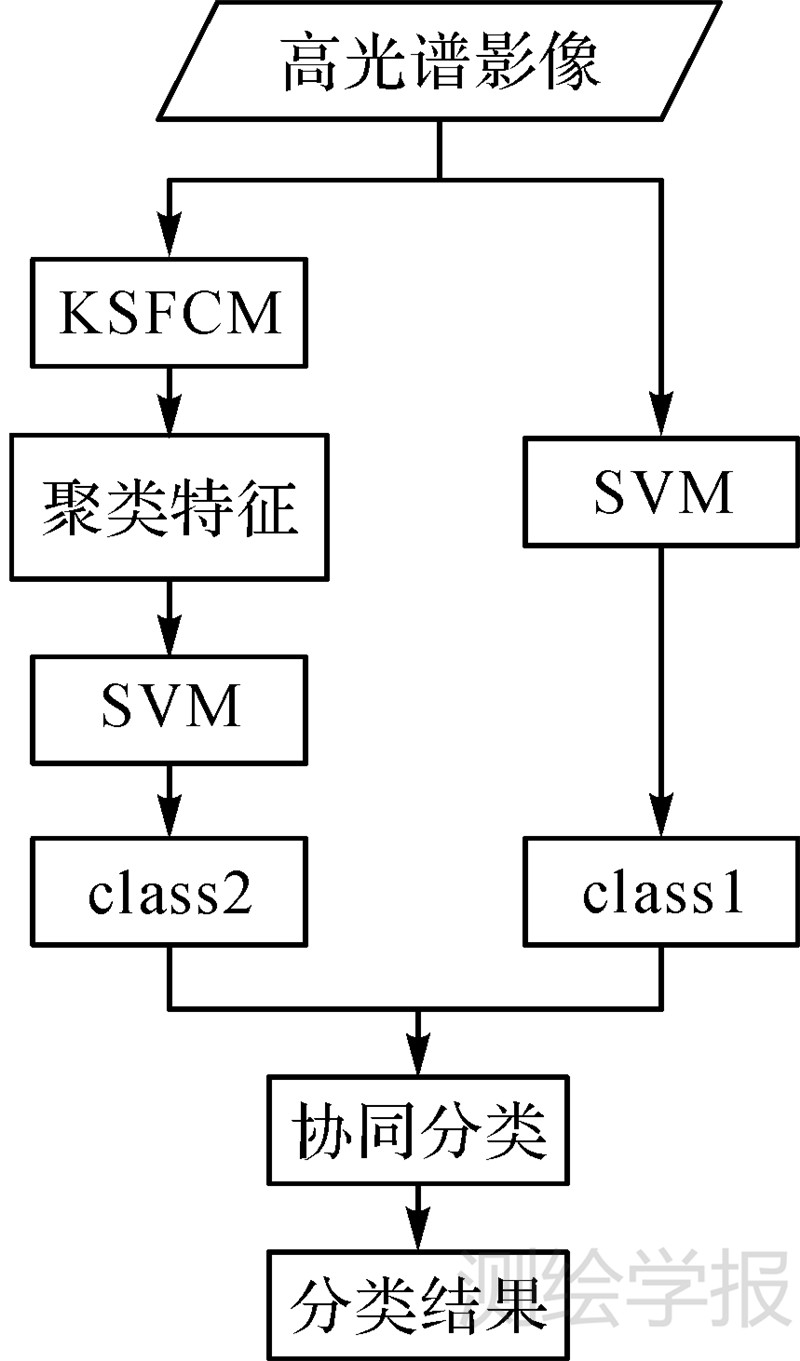
本文首先对高光谱影像原始数据利用少量类标签样本和大量无类标签样本建立SVM分类器,得到分类结果class1。然后对原始影像进行KSFCM聚类算法,得到聚类结果以及每个样本的聚类特征,由于聚类特征反映的是数据内部结构,因此对聚类特征建立SVM分类器,得到分类结果class2。最后构建协同分类框架,即利用本文提出的聚类损耗函数、分类一致函数、分类差异性、样本差异性函数使目标函数最小化,得到最佳分类结果。半监督协同分类算法流程图见图 1。
|
| 图 1 半监督协同分类算法流程图 Fig. 1 Flow chart of semi-supervised collaborative classification |
试验采用AVIRIS数据,来源于美国的普渡大学,获取时间是1992年6月,地点是印第安纳州。AVIRIS数据有220个波段,共145行、145列,包含16类地面真实类别地物,数据覆盖印第安纳西北部地区的混合农业和森林区。此数据集作为最常用的土地分类数据集,主要农作物是生长期中的玉米和大豆。原始数据经过主成分分析的RGB合成影像见图 2,普渡大学实验室提供的地面实测数据见图 3。本试验选取8类地物进行算法验证,试验中class1为玉米略耕地(corn-min),class2为玉米地(corn),class3为牧草(grass/pasture),class4为收割牧草(grass/pasture-mowed),class5为大豆未耕地(soybeans-notill),class6为大豆已耕地(soybeans-clean),class7为树林(woods),class8为玉米未耕地(corn-notill)。

|
| 图 2 RGB影像 Fig. 2 RGB image |

|
| 图 3 地面实测数据 Fig. 3 Field survey data |
对试验数据选取少量类标签样本,利用SVM算法对试验数据进行半监督分类,其中,核函数采用高斯径向基核函数,惩罚系数参数σ为0.5,间隔c为8,分类结果见图 4,总体分类精度为86.718 2%,Kappa系数0.846 7,其生产者精度和用户精度见表 1。

|
| 图 4 SVM半监督分类 Fig. 4 Semi-supervised SVM classification |
| SVM半监督 | 基于聚类特征的SVM | 本文方法 | ||||||
| 生产者精度 | 用户精度 | 生产者精度 | 用户精度 | 生产者精度 | 用户精度 | |||
| class1/(%) | 95.58 | 87.82 | 89.56 | 93.31 | 97.99 | 96.83 | ||
| class2/(%) | 100 | 86.06 | 100 | 100 | 100 | 100 | ||
| class3/(%) | 97.79 | 68.56 | 97.06 | 97.78 | 99.26 | 100 | ||
| class4/(%) | 43.66 | 83.04 | 61.03 | 84.42 | 99.06 | 96.79 | ||
| class5/(%) | 76.74 | 70.97 | 70.93 | 42.07 | 91.86 | 97.53 | ||
| class6/(%) | 99.63 | 98.55 | 100 | 100 | 100 | 100 | ||
| class7/(%) | 98.32 | 90.72 | 100 | 99.44 | 100 | 100 | ||
| class8/(%) | 79.66 | 92.61 | 90.68 | 86.99 | 96.61 | 97.44 | ||
| 总体分类精度/(%) | 86.72 | 89.68 | 98.52 | |||||
| Kappa系数 | 0.846 7 | 0.881 | 0.982 8 | |||||
对试验数据进行KSFCM聚类算法,得到隶属度矩阵U,以及每个样本的聚类特征。其中,初始聚类中心从地面实测数据中获取,根据各样本与聚类中心的光谱角大小,设定光谱角权值,得到更加精确的聚类结果。每一样本的聚类类别根据隶属度矩阵中隶属度最大的类别进行初始化,聚类结果见图 5。直接对聚类特征进行SVM分类,得到分类结果见图 6,总体分类精度为89.68%,Kappa系数0.881,虽然比半监督SVM算法精度有所提高,但是效果并不明显。

|
| 图 5 KSFCM聚类 Fig. 5 KSFCM clustering |

|
| 图 6 基于聚类特征的SVM分类 Fig. 6 SVM classification based on cluster features |
使用协同分类算法,根据聚类损耗函数、分类一致函数、分类差异性、样本差异性使目标函数最小化,从而得到最佳分类结果见图 7,总体分类精度为98.52%,Kappa系数0.9828,其生产者精度和用户精度见表 1。

|
| 图 7 半监督协同分类 Fig. 7 Semi-supervised collaborative classification |
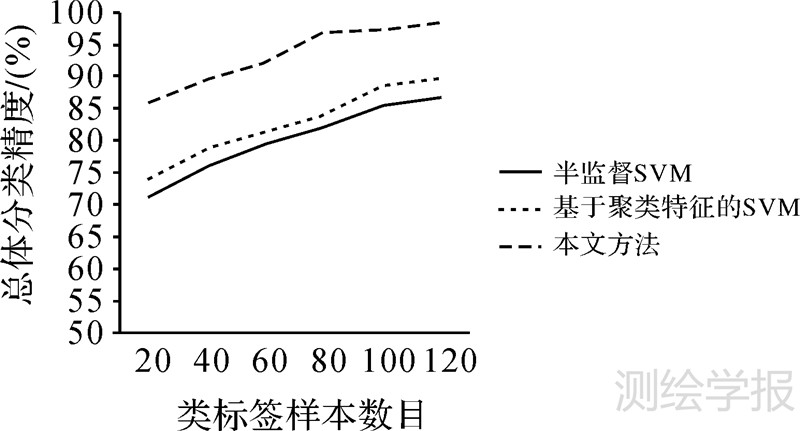
为了验证本文算法对类标签样本数量的敏感性,本文针对每一类别分别选择了20、40、60、80、100、 120个类标签样本进行试验,得到的分类精度比较图见图 8。由图 8可知,随着类标签样本的增加,分类精度逐渐提高,但是当类标签样本增加到一定程度,精度基本稳定。当类标签样本数为60,本文方法总体分类精度为92.25%,已经超过半监督SVM的最高分类精度(86.72%)和基于聚类特征的SVM最高分类精度(89.68%)。因此,本文算法能够充分利用少量类标签样本信息,得到最佳分类精度。
|
| 图 8 不同类标签样本数目下各方法的分类精度 Fig. 8 Classification accuracy of each method with different number of labeled samples |
本文算法能够结合聚类和分类的各自优势,并避免类标签样本的选取困难问题以及聚类算法隶属度最大类别作为最终样本类别造成的误分率问题。协同分类利用聚类损耗函数、分类一致函数、分类差异性、样本差异性使目标函数最小化得到最佳分类结果,通过试验得到的分类精度与直接利用SVM进行半监督分类精度相比有所提高。
5 结 论本文针对高光谱数据类标签样本获取困难的特点,提出了聚类特征和SVM组合的高光谱影像半监督协同分类新方法。该算法利用少量的类标签样本,从聚类结构的角度能够更好地反映样本空间的分布特征,从而使训练出的分类器具有更好的推广性能,一定程度上解决了支持向量数量随着训练样本增加而线性增加的问题。并且,该算法将聚类算法KSFCM与分类器SVM相结合,在协同分类框架下寻求最佳分类,避免了单独利用聚类算法进行分类造成的误分率过大问题,因此能够获得比较好的分类效果。但是本文方法目标函数需要通过多次迭代得到目标函数最小值,因此迭代运算带来的算法优化问题以及协同分类框架中各约束因子的权重问题将是下一步研究的重点。
| [1] | CAMPS-VALLS G, BANDOS MARSHEVA T, ZHOU D Y. Semi-supervised Graph-based Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3044-3054. |
| [2] | BANDOS T V, ZHOU D Y, CAMPS-VALLS G. Semi-supervised Hyperspectral Image Classification with Graphs[C]//Proceedings of IEEE International Conference on Geoscience and Remote Sensing Symposium. [S. l.]: IEEE, 2006: 3883-3886. |
| [3] | LI J, BIOUCAS-DIAS J M, PLAZA A. Semi-supervised Hyperspectral Image Classification Based on a Markov Random Field and Sparse Multinomial Logistic Regression[C]//Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium: IGARSS 2009.Cape Town: IEEE, 2009:817-820. |
| [4] | RAJAN S, GHOSH J, CRAWFORD M M. An Active Learning Approach to Hyperspectral Data Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(4): 1231-1242. |
| [5] | LI J, BIOUCAS-DIAS J M, PLAZA A. Semi-supervised Hyperspectral Image Classification and Segmentation with Discriminative Learning[C]//SPIE Europe Remote Sensing 2009. Berlin:[s.n.], 2009: 74-77. |
| [6] | RATLE F, CAMPS-VALLS G, WESTON J. Semisupervised Neural Networks for Efficient Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(5): 2271-2282. |
| [7] | GOMEZ-CHOVA L, CALPE J, CAMPS-VALLS G, et al. Semi-supervised Classification Method for Hyperspectral Remote Sensing Images[C]//2003 IEEE International Geoscience and Remote Sensing Symposium: IGARSS 03. Toulouse: IEEE, 2003: 1776-1778. |
| [8] | GÓMEZ-CHOVA L, CALPE J, SORIA E, et al. Semi-supervised Method for Crop Classification Using Hyperspectral Remote Sensing Images[C]//Recent Advances in Quantitative Remote Sensing. València: Universitat de València, 2002: 488-495. |
| [9] | MULLER K R, MIKA S, RATSCH G, et al. An Introduction to Kernel-based Learning Algorithms[J]. IEEE Transactions on Neural Networks, 2001, 12(2): 181-201. |
| [10] | CAMPS-VALLS G, BRUZZONE L. Kernel-based Methods for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(6): 1351-1362. |
| [11] | YANG Guopeng, YU Xuchu, ZHOU Xin, et al. Research on Relevance Vector Machine for Hyperspectral Imagery Classification[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 572-578. (杨国鹏, 余旭初, 周欣, 等. 基于相关向量机的高光谱影像分类研究[J]. 测绘学报, 2010, 39(6): 572-578.) |
| [12] | TAN Kun, DU Peijun. Wavelet Support Vector Machines Based on Reproducing Kernel Hilbert Space for Hyperspectral Remote Sensing Image Classification[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 142-147. (谭琨, 杜培军. 基于再生核 Hilbert 空间小波核函数支持向量机的高光谱遥感影像分类[J]. 测绘学报, 2011, 40(2): 142-147.) |
| [13] | BRUZZONE L, CHI M, MARCONCINI M. A Novel Transductive SVM for Semisupervised Classification of Remote-sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(11): 3363-3373. |
| [14] | CHI M, BRUZZONE L. Semisupervised Classification of Hyperspectral Images by SVMs Optimized in the Primal[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1870-1880. |
| [15] | BRUZZONE L, MARCONCINI M. An Advanced Semi-supervised SVM Classifier for the Analysis of Hyperspectral Remote Sensing Data[C]//Proceedings of SPIE 6365: Image and Signal Processing for Remote Sensing XII. Stockwolm: SPIE, 2006: 362-373. |
| [16] | HOSSEINI R S, HOMAYOUNI S, SAFARI R. Modified Algorithm Based on Support Vector Machines for Classification of Hyperspectral Images in a Similarity Space[J]. Journal of Applied Remote Sensing, 2012, 6(1): 355-364. |
| [17] | MARCONCINI M, CAMPS-VALLS G, BRUZZONE L. A Composite Semisupervised SVM for Classification of Hyperspectral Images[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 234-238. |
| [18] | BRUZZONE L, CHI M, MARCONCINI M. A Novel Transductive SVM for Semisupervised Classification of Remote-sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(11): 3363-3373. |
| [19] | INMACULADA D, ALBERTO V, ANTONIO P. Unsupervised Clustering and Spectral Unmixing for Feature Extraction Prior to Supervised Classification of Hyperspectral Images[C]//Proceedings of SPIE 8175: Satellite Data Compression, Communications, and Processing VII. San Diego: SPIE, 2011: 137-144. |
| [20] | TARABALKA Y, BENEDIKTSSON J A, CHANUSSOT J. Spectral: Spatial Classification of Hyperspectral Imagery Based on Partitional Clustering Techniques[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2973-2987. |
| [21] | ZHANG D Q, CHEN S C. Clustering Incomplete Data Using Kernel-based Fuzzy c-mMeans Algorithm[J]. Neural Processing Letters, 2003, 18(3): 155-162. |