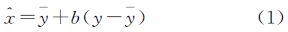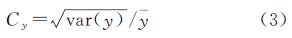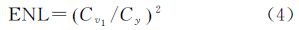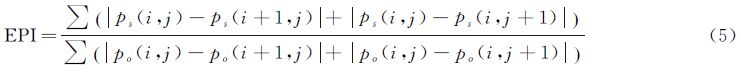1 引 言
由于SAR系统采用相干成像,SAR图像中不可避免地存在相干斑噪声。相干斑噪声降低了数据的信噪比,令SAR图像解译、参数反演等工作变得更加困难。为了减小相干斑噪声的影响,通常在进一步处理之前首先对SAR图像进行相干斑噪声滤波,以尽可能地抑制噪声,同时尽量保持图像的细节信息。因此,自从SAR系统产生以来,SAR图像滤波算法的研究就从未停止过,并且到目前为止仍然是一个热点[1, 2, 3, 4, 5, 6, 7, 8, 9]。
相对于单极化SAR,全极化SAR系统可以获取HH、HV、VH和VV共4个通道的数据,从而提供更加丰富的全极化信息。因此全极化SAR系统正在逐渐代替单极化SAR在地表分类、目标识别、变化监测、参数反演等方面扮演越来越重要的角色[20, 21, 22, 23, 24]。但同时,对于极化SAR来说,相干斑滤波不仅要分别考虑4个通道的滤波,还要考虑4个通道之间的相关性,因此相比于单极化SAR,全极化SAR图像的相干斑抑制问题更加复杂[4]。尽管如此,很多经典的极化SAR滤波算法已经被提出。文献[1]提出极化白化滤波器,通过将各极化通道最优加权组合,获得单通道的降噪图像,损失了极化信息。文献[2]提出最优加权滤波器,文献[3]提出极化矢量滤波器,均利用了乘性噪声模型和最小均方差(MMSE)思想,但是输入输出均为多通道的强度或幅度图像,不能对协方差矩阵的非对角线元素进行滤波。针对以上问题,文献[4]提出精制极化Lee滤波算法,采用非方形的边缘方向窗口达到保持边缘信息的目的,并且对协方差矩阵的所有元素利用相同的参数进行滤波,以防止通道间串扰。这种防止通道间串扰的思想对极化SAR滤波算法的研究影响深远,成为极化SAR滤波的一个基本原则[20]。虽然之后人们又提出很多优秀的极化SAR滤波算法[5, 6, 7, 8, 9],但是,精制极化Lee滤波仍然是目前应用较广泛的滤波算法[6, 21, 23]。然而,此滤波算法存在明显的缺陷:扇贝效应和虚假细线[8, 9]。因此对于有些应用如道路提取、图像分割等会造成较大影响。目前已经有一些改进的Lee滤波算法[13, 16],这些算法的改进思路主要有两个:①增加同质像素选择步骤[14, 15, 16];②令滤波窗口大小自适应[13]。第1种思路在非方形窗口中进一步筛选同质像素,会降低噪声抑制能力,增加算法复杂度;第2种思路仅能改善虚假细线问题,但不能从根本上克服这两种缺陷。本文针对这两种缺陷提出一种新的自适应增强Lee滤波算法,旨在保持原始精制极化Lee滤波简单、高效、健壮等优点的同时,克服扇贝效应和虚假细线的问题。
2 精制极化Lee滤波算法精制极化Lee滤波算法主要包括两步:模板窗口选择和局部统计滤波。具体步骤为:
(1) 模板窗口选择。将滤波窗口分解为3×3的9个子窗格,计算各子窗格内的总功率均值,然后采用如图 1所示4个边缘梯度算子进行检测,每个边缘梯度算子对应图 1(e)-(l)中每列的2个边缘方向窗口。选择梯度最大的算子所对应的两个边缘方向窗口中均值与中心像素均值比较接近的那个。
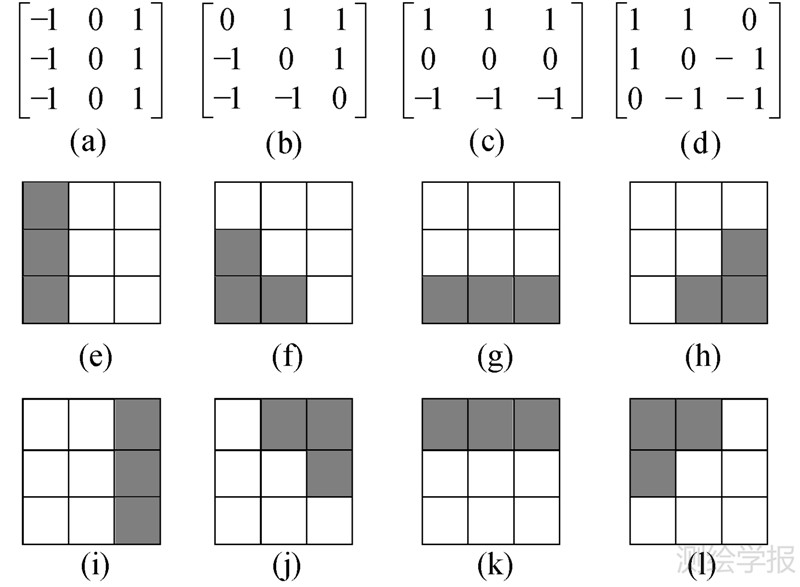
|
| 图 1 边缘梯度算子与3×3边缘方向窗口 Fig. 1 Edge gradient operators and 3×3 edge-aligned windows |
(2) 局部统计滤波。在边缘方向窗口中,利用线性最小均方差(LMMSE)滤波器进行滤波。LMMSE的数学表达式为
式中, 表示滤波后的像素值; 表示局部均值; y是中心像素值; b是权值参数,其计算公式为
表示滤波后的像素值; 表示局部均值; y是中心像素值; b是权值参数,其计算公式为
式中,var(y)表示局部方差; σv2表示噪声方差。
对于全极化SAR数据,首先用Span图像计算权重b,然后对相干矩阵或协方差矩阵的所有元素用相同的权重及滤波窗口进行滤波。
3 自适应增强Lee滤波算法 3.1 新模板设计经过试验分析发现,由于原始的精制极化Lee滤波仅定义了一组边缘方向窗口,在滤波时将均匀区域与非均匀区域都在边缘方向窗口内进行滤波。在边缘区域滤波效果很好,但是在均匀区域,由于滤波窗口的原因使得滤波后反而变得不再均匀,从而导致扇贝效应;另一方面,当滤波窗口大于图像中的线性目标宽度时,由于边缘方向窗口不能正确拟合线性目标,无论最终选择哪个边缘方向窗口,窗口内总存在异质像素,从而导致虚假细线的产生。针对以上第1个问题,可以考虑增加一个方形窗口;针对第2个问题,则需要增加一组线性方向窗口。本文所采用的线性方向窗口如图 2(a)-(d)所示,它们又分别对应图 2(e)-(l)中每列的两个线性梯度算子。在计算时,将两个算子所得梯度中较大的那个作为最终线性方向窗口的梯度。
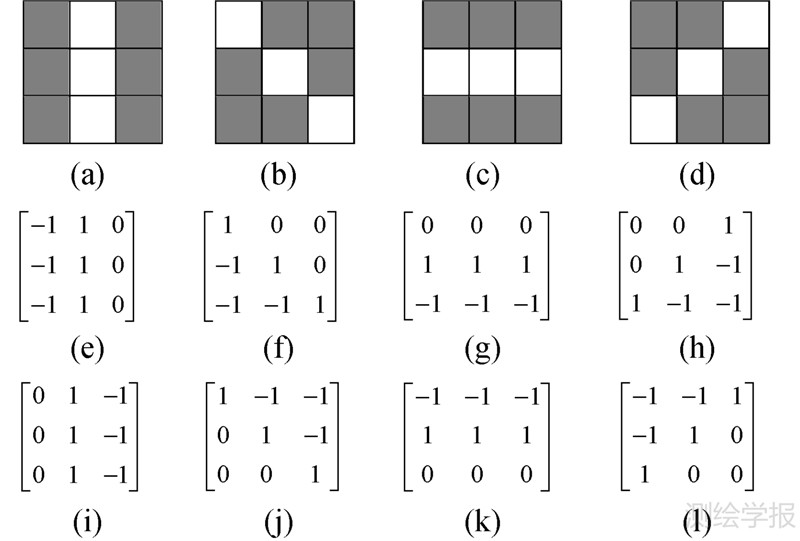
|
| 图 2 3×3线性方向窗口与线性梯度算子 Fig. 2 3 ×3 linear windows and linear gradient operators |
增加线性方向窗口后,精制极化Lee滤波效果有所改善,但是当选择较大窗口时,无论是边缘还是细线都将不能再用直线近似拟合,此时方向窗口的适应性大大下降,从而导致滤波效果的下降。为避免此问题,最好采用小窗口进行滤波。但是另一方面,对于同质区域,窗口越大,相干斑抑制能力越强,滤波效果越好。为了克服此矛盾,本文采用大小自适应的窗口:在同质度较低的区域采用小窗口进行滤波,在同质度较高的区域采用大窗口进行滤波。从而在保持图像中细节信息的同时,尽可能地提高相干斑抑制能力。
从以上分析中可以看出,自适应窗口技术的关键在于同质度量度的选择。目前提出的同质度量度主要是变差系数(CoV)[17, 18, 19],其计算公式为
但是,CoV理论阈值的设置要用到等效视数(ENL),而一幅SAR图像的ENL往往是未知的,需要事先估计。而且由于SAR图像中每个像素对应的ENL是不同的[25, 26],而需要估计的ENL只是一个全局值,并不能代表所有像素,因此会导致偏差。另外,由于CoV的物理意义不够直观,使得手动设置阈值也比较困难。基于以上原因,本文不采用CoV作为同质度度量,而提出用局部ENL作为同质度度量。强度及幅度SAR图像ENL的计算公式为
式中,Cv1表示单视SAR图像噪声的理论CoV值,对于强度图,Cv1=1,对于幅度图,Cv1=0.522 7;Cy表示SAR图像局部CoV。从式(4)中可以看出,ENL是CoV的函数,因此两者在同质度度量方面具有同等的效力。但是,由于ENL的物理意义比CoV更加直观,因此在阈值设置时更加方便。
自适应窗口技术的另一个关键问题是窗口变化顺序,即窗口是由小到大变化还是由大到小变化。文献[13]采用的是由小到大的变化策略,而本文采用由大到小的变化策略。理由如下,如果采用由小到大的变化策略,当图像噪声较严重时,小窗口计算的ENL是不可信的,而且往往是偏低的,此时会导致窗口停止增长,反映在滤波结果上,图像中会出现很多明显的椒盐状斑点。而反过来,如果采用由大到小的变化策略,先计算大窗口的ENL,则在同质区,即使噪声比较大,也能保证计算出的ENL的准确度,因此与小窗口计算的ENL相比会比较大,从而会选择大窗口进行滤波,避免了椒盐斑点的出现。
3.3 新的滤波算法基于前面的分析,本文提出一种新的自适应增强Lee滤波算法,其流程如图 3所示。具体计算步骤如下:
(1) 设置最小滤波窗口Wmin和最大滤波窗口Wmax,以及ENL阈值。由于不同大小的窗口所估计的ENL范围不同,因此其对应的阈值也应该不同,所以ENL阈值实际上是一系列阈值的集合,每个阈值对应一个窗口。令当前窗口大小W=Wmax。
(2) 利用式(4)计算W×W矩形窗口内的局部ENL,并判断是否小于阈值。如果是,则表明此窗口内像素同质度较低,转到第(3)步;如果否,则表明此窗口内像素同质度较高,因此选择方形窗口,转到第(6)步。
(3) 判断是否当前窗口大小W=Wmin。如果是,则选择非方形窗口进行滤波,转到第(4)步;如果否,令W=W-2,转到第(2)步。
(4) 将窗口分解为3×3的9个子窗口,分解方法采用精制极化Lee滤波算法中的方法,然后利用图 1和图 2中共12个梯度算子计算梯度,并求出最大梯度所对应的梯度算子代号ID。
(5) 判断是否ID∈{a,b,c,d}。如果是,则说明窗口位于边缘,此时选择梯度算子对应的两个边缘方向窗口中均值与中心像素均值较接近的那个。如果否,则说明窗口位于线上,需要进一步判断:如果ID∈{e,g,i,k},则选择线性方向窗口(图 2(a)、图 2(c))中均值与中心像素均值较接近的那个;如果ID∈{f,h,j,l},则选择线性方向窗口(图 2(b)、图 2(d))中均值与中心像素均值较接近的那个。
(6) 在所选择的窗口内利用LMMSE滤波器对极化SAR数据进行滤波。

|
| 图 3 算法流程图 Fig. 3 Flowchart of the proposed algorithm |
为了验证本文提出的滤波算法的有效性,本文分别采用机载和星载全极化SAR数据进行试验,对比分析Boxcar滤波器、精制极化Lee滤波器、改进的Sigma滤波器[8]及自适应增强Lee滤波器间的优劣。
4.1 机载数据首先采用机载全极化SAR数据进行试验。本文所使用的数据为DLR ESAR系统在德国Oberpfaffenhofen试验区获取的L波段全极化SAR数据。原始数据大小为2861像素×1540像素,为了方便展示,本文首先对其在方位向进行了2视处理,然后截取其中540像素×888像素大小的一块区域进行滤波试验。如图 4所示,为所截取区域的Pauli-RGB合成图像。从图中可以看出,试验区地物覆盖类型非常丰富,点、线、边缘等细节信息较多,并且图像中有较强的相干斑噪声。这些因素给SAR图像处理解译带来很大困难,反过来,又有利于评价滤波算法在噪声抑制、细节信息保持等方面的优劣。

|
| 图 4 ESAR L波段全极化SAR数据Pauli-RGB合成图 Fig. 4 Pauli-RGB image of ESAR L-band PolSAR data |
由于精制极化Lee滤波器采用边缘方向窗口,因此其滤波窗口中所包含的实际像素数比同尺度窗口的Boxcar滤波器所包含的像素数要少。为达到相当的相干斑抑制效果,精制极化Lee滤波器的窗口需要设置的比Boxcar滤波器的窗口略大。并且在选择窗口大小时为了保持细节信息,往往设置为与图像中点、线等目标的尺寸相当。对于改进的Sigma滤波器和自适应增强Lee滤波器,由于其实际参与滤波的像素数是自适应的,因此可以选择较大的滤波窗口,不会导致细节信息的严重丢失。本小节中考虑试验数据中点、线等细节信息的尺寸,分别用5×5的Boxcar滤波器、7×7的精制极化Lee滤波器、11×11的改进的Sigma滤波器及最小窗口为3×3、最大窗口为11×11的自适应增强Lee滤波器对试验数据进行滤波处理,所得部分结果如图 5所示。

|
| 图 5 滤波结果对比图 Fig. 5 Comparison of different filters |
从图中可以看出,精制极化Lee滤波结果中有明显的扇贝效应(图 5(a)中区域1),并且在暗线中心有虚假亮线(图 5(a)中区域2)。而自适应增强Lee滤波结果在同质区域滤波效果较平滑,并且能很好地保持点、线等细节信息(图 5(b))。为了定量评价滤波器的边缘保持能力,根据以下边缘保持指数(EPI)[27]公式对几种滤波结果进行比较
利用Span图计算得到的结果如表 1所示。从表 1可以看出,自适应增强Lee滤波的EPI比Boxcar和精制极化Lee滤波都高。但是改进的Sigma滤波EPI却远远高于其他滤波器。其中部分原因是因为改进的Sigma滤波对散射回波较高的像素不进行滤波处理,因此与原始图像是一样的。从式(5)中可以看出,如果滤波前后像素值不变,则EPI为1,从而这些未滤波的像素使EPI估计值偏高。另外,从表 2中可以看出,改进的Sigma滤波噪声抑制能力比自适应增强Lee滤波弱,因此其高EPI是以弱噪声抑制力为代价的。
| 滤波方法 | EPI |
| 原始图像 | 1 |
| Boxcar | 0.306 |
| 精制极化Lee | 0.354 |
| 改进的Sigma | 0.754 |
| 自适应增强Lee | 0.412 |
| 区域1 | 区域2 | 区域3 | 平均 | |
| 原始图 | 0.686 3 | 0.665 7 | 0.720 2 | 0.690 7 |
| Boxcar | 0.231 4 | 0.244 1 | 0.275 8 | 0.250 4 |
| 精制Lee | 0.199 0 | 0.209 8 | 0.253 7 | 0.220 8 |
| Sigma | 0.183 3 | 0.258 3 | 0.239 2 | 0.226 9 |
| 自适应增强Lee | 0.158 2 | 0.156 7 | 0.212 7 | 0.175 9 |
为了进一步评价滤波器在噪声抑制方面的能力,选择如图 4所示3个矩形区域,利用Span图统计其滤波前后的CoV值,统计结果见表 2。从表 2中可以看出,精制Lee滤波与改进的Sigma滤波的噪声抑制效果大致相当,略优于Boxcar滤波,而本文提出的自适应增强Lee滤波所得CoV值明显低于其他滤波结果,具有最优的噪声抑制能力。
4.2 星载数据本小节利用ALOS PALSAR系统对武汉市获取的全极化SAR数据进行进一步试验。原始数据大小为18 432像素×1248像素,为了方便展示,本文首先对其在方位向进行了8视处理,然后截取其中460像素×640像素大小的一块区域进行滤波试验。如图 6所示,为所截取区域的Pauli-RGB合成图像。从图中可以看到,试验区地物覆盖情况非常复杂,河流、湖泊、道路纵横交错,线性目标非常丰富,并且图像中同样伴有明显的相干斑噪声。

|
| 图 6 PALSAR L波段全极化SAR数据Pauli-RGB合成图 Fig. 6 Pauli-RGB image of PALSAR L-band PolSAR data |
考虑试验数据中点、线等细节信息的尺寸,分别用3×3的Boxcar滤波器、5×5的精制极化Lee滤波器、7×7的改进的Sigma滤波器及最小窗口为3×3、最大窗口为7×7的自适应增强Lee滤波器对试验数据进行滤波处理,所得部分结果如图 7所示。从图中可以看出,精制极化Lee滤波结果在暗线中心有明显的虚假亮线(图 7(a)中区域1),并且较小的水体(可视为暗的点目标)及较细的亮线会被模糊掉(图 7(a)中区域2)。而自适应增强Lee滤波能很好地保持暗线、亮线、暗的点目标等细节信息,并且在同质区域滤波效果比精制极化Lee滤波更加平滑(图 7(b))。

|
| 图 7 滤波结果对比图 Fig. 7 Comparison of different filters |
利用Span图计算滤波前后EPI,得到的结果如表 3所示。从表 3可以看出,自适应增强Lee滤波的EPI远高于精制极化Lee滤波,但低于改进的Sigma滤波。
| 滤波方法 | EPI |
| 原始图像 | 1 |
| Boxcar | 0.357 |
| 精制极化Lee | 0.279 |
| 改进Sigma | 0.608 |
| 自适应增强Lee | 0.490 |
为了进一步评价自适应增强Lee滤波对极化散射特性的保持效果,选取图 6中所示的一小块同质区域,绘制其滤波前后平均相干矩阵的极化响应图,结果如图 8所示。从图中可以看出,滤波前后共极化与交叉极化的极化响应图均有高度的一致性,说明自适应增强Lee滤波 器能很好地保持图像中地物的极化散射特性。

|
| 图 8 滤波前后共极化与交叉极化的极化响应图 Fig. 8 The original and filtered co-polarization and cross-polarization signatures |
本文针对精制极化Lee滤波结果中存在扇贝效应和虚假细线的问题,提出增加一组均匀窗口及一组线性方向窗口,并采用大小自适应窗口机制,在同质度高的区域用大窗口滤波,在同质度低的区域用小窗口滤波,从而使得滤波窗口在形状和尺寸上都能自动适应实际场景。利用机载和星载全极化SAR数据进行的滤波试验结果表明,本文提出的自适应增强Lee滤波算法在同质区域的噪声抑制能力明显强于精制极化Lee滤波算法及改进的Sigma滤波算法,同时在保持较暗的与较亮的点、线等细节信息方面也优于精制极化Lee滤波算法,并且能很好地保持图像中地物的极化散射信息。
然而,由于窗口自适应机制需要设置更多的参数,尤其是同质度阈值参数的设置,使得自适应增强Lee滤波算法在易用性上面不如精制极化Lee滤波。后续将研究同质度参数阈值的自适应设置方法,提高算法的易用性。
| [1] | NOVAK L M, BURL M C. Optimal Speckle Reduction in Polarimetric SAR Imagery[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(2): 293-305. |
| [2] | LEE J, GRUNES M R, MANGO S A. Speckle Reduction in Multipolarization, Multifrequency SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(4): 535-544. |
| [3] | GOZE S, LOPES A. A MMSE Speckle Filter for Full Resolution SAR Polarimetric Data[J]. Journal of Electromagnetic Waves and Applications, 1993, 7(5): 717-737. |
| [4] | LEE J S, GRUNES M R, DE GRANDI G. Polarimetric SAR Speckle Filtering and Its Implication for Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2363-2373. |
| [5] | VASILE G, TROUVE E, BUZULOIU V. Intensity-driven Adaptive-neighborhood Technique for Polarimetric and Interferometric SAR Parameters Estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(6): 1609-1621. |
| [6] | LEE J, GRUNES M R, SCHULER D L, et al. Scattering-model-based Speckle Filtering of Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1): 176-187. |
| [7] | LOPEZ-MARTINEZ C, FABREGAS X. Model-based Polarimetric SAR Speckle Filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3894-3907. |
| [8] | LEE J, WEN J-H, AINSWORTH T L, et al. Improved Sigma Filter for Speckle Filtering of SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 202-213. |
| [9] | CHEN J, CHEN Y, AN W, et al. Nonlocal Filtering for Polarimetric SAR Data: A Pretest Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1744-1754. |
| [10] | HUANG Shiqi, LIU Daizhi. Research on Method and Application of Speckle Noise Reduction of SAR Image[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 245-250. (黄世奇,刘代志.SAR图像斑点噪声抑制方法与应用研究[J].测绘学报,2006, 35(3): 245-250.) |
| [11] | YANG Shenbin, LI Bingbai, SHEN Shuanghe, et al. Structure Retaining Linear Multi-channel SAR Image Speckle Filter[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 364-370. (杨沈斌,李秉柏,申双和,等.基于特征保持的线性多通道最优求和SAR图像滤波算法[J].测绘学报, 2006, 35(4): 364-370.) |
| [12] | ZHANG Zhongshan, YU Jie, YAN Qin, et al. Research on Polarimetric SAR Image Speckle Reduction Using Kernel Independent Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 289-295. (张中山,余洁,燕琴,等.基于核独立成分分析的极化SAR图像相干斑抑制[J].测绘学报,2011,40(3):289-295.) |
| [13] | JIANG Yong, ZHANG Xiaoling, SHI Jun. Speckle Reduction for Polarimetric SAR Images by Improved Lee Filter [J]. Journal of University of Electronic Science and Technology of China, 2009, 38(1): 5-8. (江勇, 张晓玲, 师君. 极化SAR改进Lee滤波相干斑抑制研究 [J]. 电子科技大学学报, 2009, 38(1): 5-8.) |
| [14] | YANG Dahai, MA Debao. Refined Polarimetric SAR Speckle Lee Filtering Algorithm Based on Relativity of Polarization Vector[J]. Journal of Information Engineering University, 2010, 11(6): 737-740. (杨大海, 马德宝. 基于极化矢量相似系数的极化Lee滤波改进算法[J]. 信息工程大学学报, 2010, 11(6): 737-740.) |
| [15] | OUYANG Qundong, WU Zhaocong, PENG Jiangui. An Improved Method of Lee Refined Polarized Filter[J]. Science of Surveying and Mapping, 2011, 36(5): 136-138. (欧阳群东, 巫兆聪, 彭检贵. 一种改进的精制极化Lee滤波算法[J]. 测绘科学, 2011, 36(5): 136-138.) |
| [16] | LIU Rong, LOU Xiaoguang. An Improved Speckle Reducing Algorithm for Lee Filtering Based on Edge Direction[J]. Science Technology and Engineering, 2011, 11(11): 2497-2501. (刘蓉, 娄晓光. 基于边缘特性的极化Lee滤波改进算法 [J]. 科学技术与工程, 2011, 11(11): 2497-2501.) |
| [17] | NEZRY E, LOPES A, TOUZI R. Detection of Structural and Textural Features for SAR Images Filtering[C]// IGARSS ’91: Proceedings of IEEE 1991 International Geoscience and Remote Sensing Symposium.Espoo: IEEE, 1991: 2169-2172. |
| [18] | NICOLAS J M, TUPIN F, MAITRE H. Smoothing Speckled SAR Images by Using Maximum Homogeneous Region Filters: An Improved Approach[C]// IGARSS ’01: Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium. Sydney: IEEE, 2001: 1503-1505. |
| [19] | TOUZI R. A Review of Speckle Filtering in the Context of Estimation Theory[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2392-2404. |
| [20] | LEE J, POTTIER E. Polarimetric Radar Imaging: From Basic to Application[M]. New York: CRC Press, 2009. |
| [21] | YANG Jie, LANG Fengkai, LI Deren. An Unsupervised Wishart Classification for Fully Polarimetric SAR Image Based on Cloude-Pottier Decomposition and Polarimetric Whitening Filter [J]. Geomatics and Information Science of Wuhan University. 2011, 36(1): 104-107. (杨杰,郎丰铠,李德仁.一种利用 Cloude-Pottier分解和极化白化滤波的全极化SAR图像分类算法[J].武汉大学学报: 信息科学版, 2011, 36(1): 104-107.) |
| [22] | LANG Fengkai, YANG Jie, ZHAO Lingli, et al. Polarimetric SAR Data Classification with Freeman Entropy and Anisotropy Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 556-562. (郎丰铠,杨杰,赵伶俐,等.基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J].测绘学报, 2012, 41(4): 556-562.) |
| [23] | YANG Jie, ZHAO Lingli, SHI Lei, et al. Interpretation of Oblique Buildings Based on Optimal Polarimetric Coherence Coefficient[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 577-583. (杨杰,赵伶俐,史磊,等.基于最优极化相干系数的倾斜建筑物解译研究[J].测绘学报, 2012, 41(4): 577-583.) |
| [24] | TAN Lulu, YANG Libo, YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 296-300. (谈璐璐,杨立波,杨汝良.基于ESPRIT算法的极化干涉SAR植被高度反演研究[J].测绘学报, 2011, 40(3): 296-300.) |
| [25] | ANFINSEN S N, DOULGERIS A P, ELTOFT T. Estimation of the Equivalent Number of Looks in Polarimetric Synthetic Aperture Radar Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(11): 3795-3809. |
| [26] | CUI Y, ZHOU G, YANG J. Unsupervised Estimation of the Equivalent Number of Looks in SAR Images[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 710-714. |
| [27] | HAN Chunming, GUO Huadong, WANG Changlin, et al. Edge-preserving Filter for SAR Images[J]. High Technology Letters, 2003, 13(7): 11-15. (韩春明,郭华东,王长林,等.保持边缘的SAR图像滤波方法[J].高技术通讯,2003, 13(7): 11-15.) |