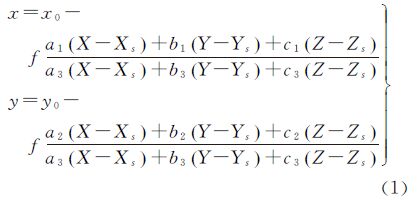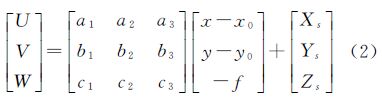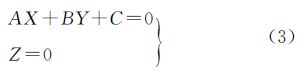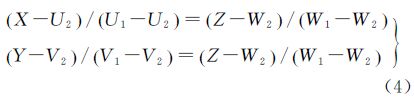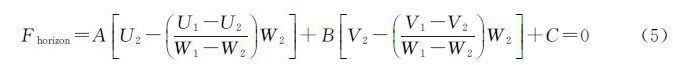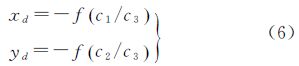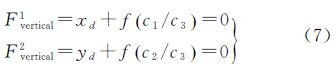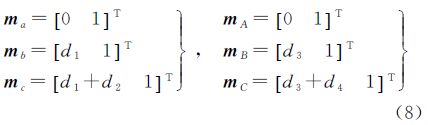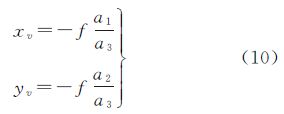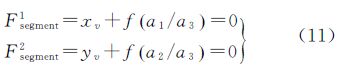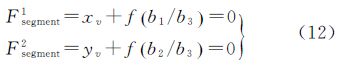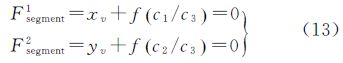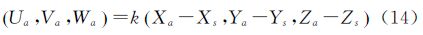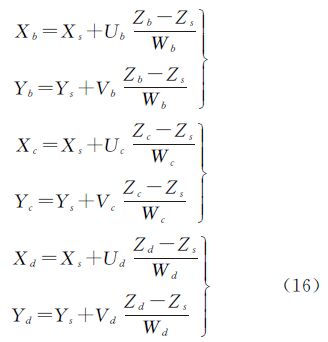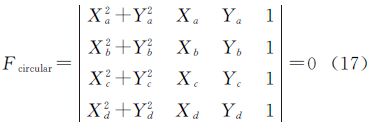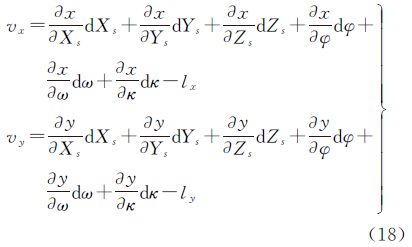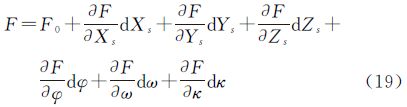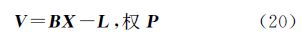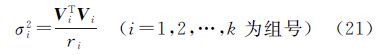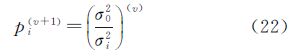2. 浙江省地理信息中心，浙江 杭州 310012
2. Geographic Information Center of Zhejiang Province，Hangzhou 310012，China
1 引 言
后方交会是摄影测量、计算机视觉等相关领域的一个基础性问题，它是通过一定的物方控制点及其在影像上对应像点的坐标反算出相机的位置与姿态(也称为相机的外方位元素)。它的解法有多种，如共线条件方程法[1, 2]、角锥体法[3, 4]、直接线性变换法[5, 6]以及四元数法[7, 8, 9, 10]。其中，共线方程法需要已知外方位元素的初始值，一般适用于垂直摄影；角锥体法也需要已知外方位线元素的初始值；直接线性变换法无须初始值，适合于非量测相机，能够满足中、低精度的测量任务；四元数法是利用数学意义上的四元数来描述相机的旋转矩阵，可以解决大倾角影像后方交会计算中初值不易选择的问题。上述方法各有其独自的优点与适用范围，主要是基于点来计算相机的外方位元素，但在相机成像的过程中，除了点之外，还存在着直线、曲线等几何要素以及灭点、绝对二次曲线等概念要素。这些要素在投影变换中也蕴含了相机方位元素的相关信息，它们也可以用来求解相机的外方位元素。
广义点摄影测量理论[11]扩展了共线方程的使用范围，使其不再仅仅满足空间点与像点之间严格的对应关系，这非常适用于特征点较少但存在其他几何特征情况下的相关问题求解。基于该理论的相关方法已经在相对定向、绝对定向、三维重建等方面取得了较好的应用。文献[12, 13]基于广义点摄影测量理论提出了利用铅垂线辅助的城区影像的绝对定向与空中三角测量；文献[14, 15, 16]是借助于广义点摄影测量理论在工业摄影测量方面的应用；文献[17, 18]也基于广义点摄影测量理论提出了综合多种同名特征的航空影像相对定向方法。
本文在此基础上提出了一种综合多种特征的后方交会法，该方法将水平线、垂直线、线段与水平圆等多种特征都纳入共线方程，构成统一的平差解算模型，能够较大程度上减少传统后方交会法对特征点数量与分布的依赖，使基于共线方程的后方交会法具有更广的适用范围。在特征点数量一定的情况下，该方法由于引入了更多的观测量，也能够在一定程度上提高计算结果的精度和稳定性。
2 多种特征的后方交会传统摄影测量中的“点”指的是物理意义上的点，如圆点、端点、交叉点、拐点等，在现实世界中除了物理点外还存在着大量的线，如直线、曲线等，另外还有一些概念上的点或线，如灭点、绝对二次曲线等。将摄影测量中的一些特征归结为“点”，代入共线方程，进行统一平差，即所谓的广义点摄影测量。将尽可能多的数学特征归结为“点”，既能够在一定程度上提高计算结果的精度，也能够减少对“物理”意义上对应点的依赖。因此，基于该理论的方法非常适用于特征点相对较少、先验知识比较缺乏的特殊环境。
摄影测量的基本理论公式为[1]
式中，(x,y)为像点坐标；(x0,y0)为像主点坐标；(X,Y,Z)表示物方点在地面测量坐标系中的坐标；(Xs,Ys,Zs)表示相机所在的位置；f为相机的焦距；[ai bi ci] (i=1，2，3)表示旋转矩阵，是影像外方位角元素φ、ω、κ的函数。另外，像点在像空间直角坐标系的坐标(x,y,-f)与在地面测量坐标系的坐标(U,V,W)之间的转换关系为
本文主要分析了水平线、垂直线、线段与水平圆对相机外方位元素的几何约束，为了简化公式，影像点的坐标主要使用的是像点在地面测量坐标系中的(U,V,W)坐标。因此，基于式(2)可以实现相机外方位元素、像点坐标观测值与中间变量(U,V,W)之间的转换。
2.1 水平线如图 1所示，若在地面P上存在水平线L，线上有M、N两点，它在像平面P0的成像为l，线上有m、n两点，其中M、m、N、n不要求互为对应点。
|
| 图 1 基于水平线的几何关系 Fig. 1 Geometric relationships based on horizon lines |
假设地面P的高程值Z为0，则可以列出L在地面测量坐标系中的直线方程为
式中，A、B、C为直线方程的系数，将直线方程进行归一化处理，即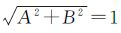
，然后可以由地面P上的M、N两点计算得出。设在地面测量坐标系中m点的坐标为(U1,V1,W1),n点的坐标为(U2,V2,W2)，可以列出l在地面测量坐标系中的直线方程为
由于直线L与l的相交于c点，且c点也在地面P上，因此，c的Z值为0，再将式(4)代入式(3)，并结合c点Z值为0的条件可以推导得出
式中的地面测量坐标(U1,V1,W1)与(U2,V2,W2)可以由m点与n点像点坐标观测值代入式(2)求得，Fhorizon表示由水平线所提供的等量关系，以该等量关系可以对相机的外方位元素提供一个约束条件。
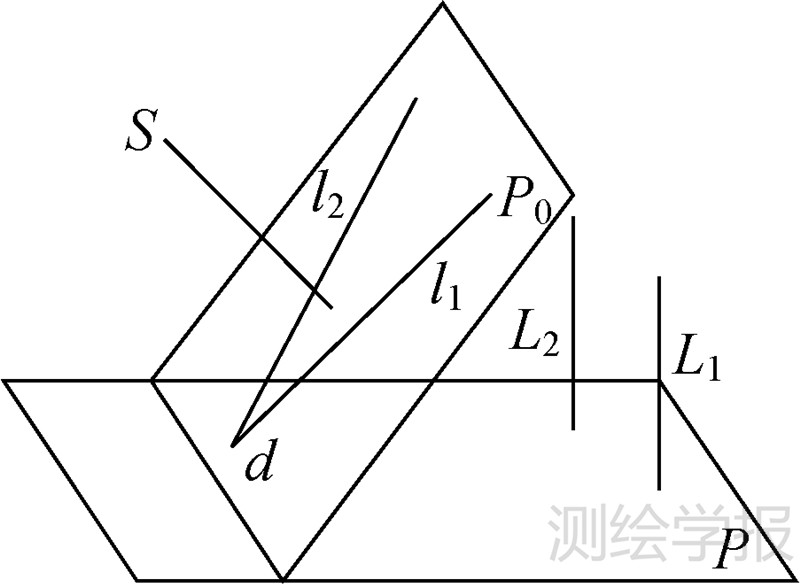
2.2 垂直线根据计算机视觉与摄影测量的灭点理论，物方空间的一组平行线在影像平面上的中心投影应当严格的相交于一点[5]，即所谓的灭点。而垂直线是一组特殊的平行线，它在影像平面上的灭点既是投影垂直线的交会点，也是通过投影中心的垂直线与像平面的交点，称为像底点。如图 2所示，设地面上存在垂直线L1与L2，在像平面上的成像为L1与L2，交点为d，那么d点即为像底点，对应于过投影中心的垂直线上的无穷远点(Xd,Yd,Zd)，因此，Xd=Xs，Yd=Ys，Zd=∞，代入式(1)可以求得像底点的像平面坐标为
式中，像底点(xd,yd)可以用两条或多条垂直线的投影直线相交求得，以该等量关系可以对相机的内方位元素中的f与外方位角元素提供两个约束条件
|
| 图 2 基于垂直线的几何关系 Fig. 2 Geometric relationships based on vertical lines |
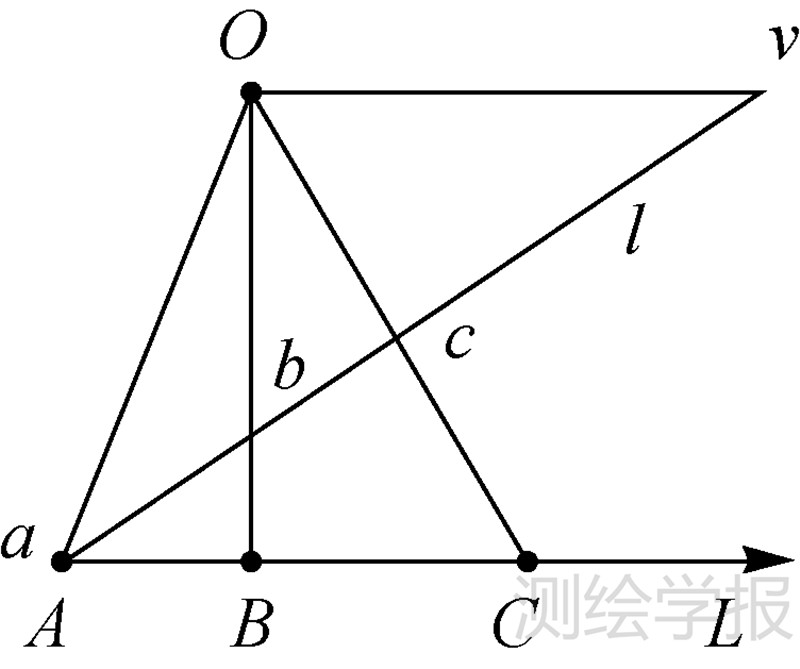
若视场中存在可以量测间距的线段，则由此可以计算出该线段方向上的灭点。如图 3所示，像平面上有直线l，线上存在端点a、b、c，间距比为d(a,b):d(b,c)=d1:d2。以a为端点作另外一条直线L，设L上有端点A、B、C，其中A点与a点重合，其他几点的间距比为d(A,B):d(B,C)=d3:d4，再连接Cc与Bb的延长线交于O点，可以认为直线l是直线L的一维投影所成的像[4]，O点为投影中心，a、b、c是A、B、C 3点一维投影所成的像。则可以列出上述6个点的一维齐次坐标与转换关系为
式中，H2×2为一维投影变换矩阵，自由度为3，由上述3组对应点可以计算得出该变换矩阵。则L上的无穷远点[1 0]T乘以H2×2，就可以算出l上灭点v的坐标。
再假设该直线l所对应的物方直线的方向即为地面测量坐标系中的X轴方向，将式(1)中两个等式的右端分子分母均除以X，并令X趋于无穷远，可以获得平行于X轴直线方向上对应灭点v的方程为
因此，一条已知间距的线段可以对相机内方位元素f与外方位角元素提供两个约束条件
同理，若l所对应的物方直线的方向为地面测量坐标系中的Y轴或Z轴的方向，则可以获得约束条件式(12)或式(13)
2.4 水平圆
如图 4所示，a、b、c、d分别为地面圆形上的任意4点A、B、C、D所对应的像点，设A的坐标为(Xa,Ya,Za)，a点在地面测量坐标系中的坐标为(Ua,Va,Wa)，由三点共线可得
式中，k为比例系数，化简后得
同理可得B、C、D的关系
设该圆所在面为水平面，则可令Za=Zb=Zc=Zd=0，结合克莱姆法则平面上四点共圆的充要条件为
再将式(15)、式(16)代入式(17)，可以得到4个像点地面测量坐标的关系方程，再结合式(2)转换为像点坐标与外方位元素的关系方程，能够对外方位元素提供一个约束条件。
|
| 图 4 基于水平圆的几何关系 Fig. 4 Geometric relationships based on circle |
传统摄影测量中利用特征点求解相机外方位元素的线性化误差方程式为式(18)，再结合式(5)、式(7)、式(11)、式(17)可以列出水平线、垂直线、线段与水平圆的线性化误差方程式为式(19)。其中，F0为外方位元素的近似值分别代入对应式所计算的F值，dXs、dYs、dZs、dφ、dω、dκ为外方位元素近似值的改正数，联合式(18)与式(19)可以列出统一的平差模型为式(20)
其中，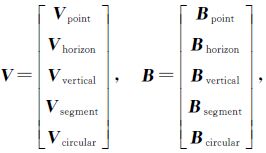
式(20)中的X为外方位元素近似值的改正数;Vpoint、Vhorizon、Vvertical、Vsegment、Vcircular分别为特征点、水平线、垂直线、线段、水平圆的观测值改正数；Bpoint、Bhorizon、Bvertical、Bsegment、Bcircular为相应的系数矩阵；Lpoint、Lhorizon、Lvertical、Lsegment、Lcircular为相应观测值的残差项；Ppoint、Phorizon、Pvertical、Psegment、Pcircular为各个观测值的权值，可以由观测值的可靠性、稳定度与多余观测来决定[19]。具体的定权方法可以通过选权迭代的方式来实现：将特征点、水平线、垂直线、线段、水平圆划分为不同组的观测值，设每组内的观测值具有相同的精度，观测值互不相关，则可按FÖrstner提出的方法来计算各组观测值的后验方差[20]
式中，ri=ni-pitr(AiQAiT)，是该组观测值多余观测数的分量。其中，Q为权系数矩阵；ni为该组的观测值个数；pi是该组观测值的权值，迭代初始值设定为1，则下一步迭代中各组观测值的权为
式中，v为迭代次数；σ0为单位权均方差，计算方法为
式中，r是总的多余观测数。
至此，就将常规意义上的特征点与水平线、垂直线、线段与水平圆纳入了统一的平差模型中，构建方程式的对应关系已经不再局限于狭义上的点与点之间的对应。另外，后方交会计算过程中共有6个未知数，理论上讲3个特征点就可以计算出外方位元素(为了保证数据的可靠性，一般多于3个特征点)，加入多种特征后，相对于传统的共线方程，水平线与水平圆可以提供1个约束条件，垂直线与线段可以提供两个约束条件。
3 试验与讨论为了验证该方法的正确性和实用性，特别是在特征点较少情况下对相机的定位效果，分别进行了模拟数据与真实数据的对比试验。
3.1 模拟数据模拟试验所采用的方法是先给出特征点的地面坐标和外方位元素的模拟值，然后根据严格的共线方程生成模拟的像点坐标数据，在像点坐标值中加入高斯噪声以模拟像点的观测值，再利用上述的方法来解算影像的外方位元素，以计算结果的均方差来检验方法的正确性与有效性。
模拟生成的影像包括6个特征点、4条水平线、4条垂直线、3条线段以及2个水平圆，在影像上均匀分布；模拟的影像数据分为3组，分别模拟近景影像、航空大倾角影像与航空小倾角影像，相关参数如表 1所示。
| 数据类别 | Xs/m | Ys/m | Zs/m | φ/rad | ω/rad | κ/rad | f/mm | 像素大小/μm |
| 近景影像 | 35 | 166 | 1 | 1.605 7 | 0.558 5 | 0 | 20 | 8 |
| 航空大倾角影像 | 1500 | 1500 | 2000 | 0.785 4 | 0.785 4 | 0.523 6 | 100 | 12 |
| 航空小倾角影像 | 3500 | 3500 | 2000 | 0.087 2 | 0.087 2 | 0 | 100 | 12 |
在所有模拟的像点坐标值中加入均值为0、均方差为两个像素的高斯噪声，进行对比试验，结果如表 2所示，表中的(pt.sp.cz.xd.yh)依次表示特征点、水平线、垂直线、线段与水平圆的个数，计算结果均取小数点后6位。另外，为了保证多条线段的约束条件同时有效，模拟的3条线段是相互垂直的。
| (pt.sp.cz.xd.yh) | σXs/m | σYs /m | Zs/m | σφ/rad | σω/rad | σκ/rad | |
| 模拟近景影像计算结果值 | (6.0.0.0.0) | 0.003 023 | 0.004 139 | 0.004 023 | 0.000 393 | 0.000 313 | 0.000 378 |
| (4.4.0.0.0) | 0.004 287 | 0.005 719 | 0.005 990 | 0.000 428 | 0.000 674 | 0.000 796 | |
| (4.0.4.0.0) | 0.003 923 | 0.004 843 | 0.004 523 | 0.000 311 | 0.000 591 | 0.000 780 | |
| (4.0.0.3.0) | 0.002 694 | 0.004 936 | 0.004 815 | 0.000 299 | 0.000 468 | 0.000 681 | |
| (4.0.0.0.2) | 0.005 001 | 0.005 123 | 0.004 089 | 0.000 422 | 0.000 337 | 0.000 678 | |
| (6.4.4.3.2) | 0.001 972 | 0.001 174 | 0.002 023 | 0.000 207 | 0.000 190 | 0.000 223 | |
| 模拟航空大倾角影像计算结果值 | (6.0.0.0.0) | 0.007 258 | 0.006 876 | 0.007 023 | 0.001 142 | 0.000 891 | 0.000 871 |
| (4.4.0.0.0) | 0.007 921 | 0.008 625 | 0.009 990 | 0.001 365 | 0.001 204 | 0.001 541 | |
| (4.0.4.0.0) | 0.009 384 | 0.007 731 | 0.007 523 | 0.000 954 | 0.000 879 | 0.001 336 | |
| (4.0.0.3.0) | 0.008 120 | 0.008 976 | 0.008 289 | 0.001 123 | 0.001 321 | 0.000 891 | |
| (4.0.0.0.2) | 0.011 514 | 0.009 857 | 0.011 081 | 0.001 545 | 0.000 979 | 0.001 102 | |
| (6.4.4.3.2) | 0.006 765 | 0.005 619 | 0.004 223 | 0.000 897 | 0.000 521 | 0.000 456 | |
| 模拟航空小倾角影像计算结果值 | (6.0.0.0.0) | 0.005 984 | 0.004 341 | 0.005 651 | 0.000 741 | 0.000 693 | 0.000 794 |
| (4.4.0.0.0) | 0.006 321 | 0.006 787 | 0.005 365 | 0.000 684 | 0.000 701 | 0.000 820 | |
| (4.0.4.0.0) | 0.007 251 | 0.005 556 | 0.007 477 | 0.000 732 | 0.000 745 | 0.000 729 | |
| (4.0.0.3.0) | 0.007 761 | 0.008 592 | 0.007 842 | 0.000 822 | 0.000 893 | 0.000 895 | |
| (4.0.0.0.2) | 0.008 618 | 0.009 265 | 0.008 029 | 0.000 758 | 0.001 016 | 0.000 967 | |
| (6.4.4.3.2) | 0.004 441 | 0.002 313 | 0.002 321 | 0.000 443 | 0.000 337 | 0.000 423 | |
从表 2可以看出：在模拟的3种影像环境下，利用少量的特征点与水平线、垂直线、线段与水平圆进行综合求解均可以获得比较理想的结果，证明了综合多种特征的后方交会法有比较广泛的适用范围。再比较各组数据在不同约束条件下的外方位元素计算结果的均方差可以看出：6个特征点联合4个水平线、4个垂直线、3个线段与2个水平圆计算获得的均方差最小，对噪声的敏感性最低，这也说明了联合更多的几何特征与特征点进行求解，对噪声的抑制能力更强。
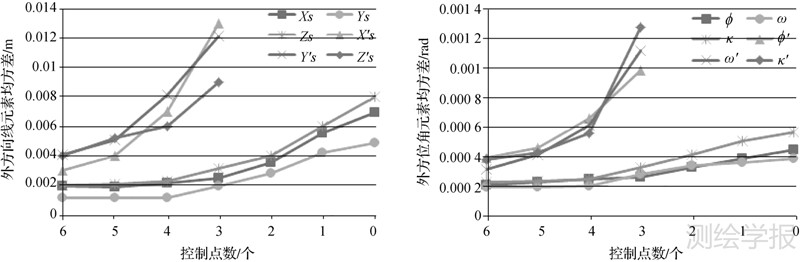
另外，为了进一步分析在特征点逐渐减少情况下综合多种特征后方交会法的效果，以上述模拟的近景试验数据为例，作两组对比试验：使用6个特征点作为控制条件，进行传统后方交会计算；使用6个特征点加上4条水平线、4条垂直线、3条线段以及2个水平圆作为控制条件，进行综合多种特征的后方交会计算。逐渐减少两组对比试验中的特征点的个数，以外方位元素结果值的均方差为评价依据，结果如图 5所示，图中的(Xs′，Ys′，Zs′，φ′，ω′，κ′)为仅使用特征点的后方交会法结果；(Xs，Ys，Zs，φ，ω，κ)为综合多种特征的后方交会法结果。
|
| 图 5 减少特征点情况下两种后方交会方法对比结果 Fig. 5 The results of two space resection method under the reducing control points |
从图 5可以看出，综合多种特征后方交会法相对于传统后方交会法外方位元素计算结果的均方差更小，随着特征点数量逐渐减少，前者均方差的增长幅度也更小一些。另外，当特征点数量少于3个，传统后方交会法无法进行计算时，综合多种特征的后方交会法依然能够求得比较合理的结果值。因此，综合多种特征后方交会法能够在一定程度上解决特征点不足时的后方交会难题。同时，引入多余的观测量也能在一定程度上提高计算结果的精度与稳定性。
3.2 真实数据如图 6所示，试验数据为同一场景的两幅航空影像，影像大小为3000像素×4000像素，镜头焦距为105.2 mm，像素大小为0.009 mm。
|
| 图 6 基于多种特征的后方交会影像图 Fig. 6 Space resection based on multiple features |
在该场景中选取8个特征点，分别以全部的8个特征点(图 6中以“×”与“+”表示)和其中的4个特征点(图 6中以“×”表示)为控制条件，使用传统后方交会法计算两幅影像的外方位元素。再以其中的4个特征点加上3条水平线、3条垂直线与4个水平圆为控制条件，使用综合多种特征的后方交会法计算两幅影像的外方位元素。为了评价3组试验的结果，引入6个检查点(图 6中以“Δ”表示)以检验物方实际测量点的精度，考虑到单张影像无法获得物方点的三维坐标值，所以采用该航向相邻的两张影像通过“后方交会+前方交会”的计算方式得到6个检查点的物方三维坐标值，验证结果如表 3所示。另外，在表 4中列出了综合多种特征后方交会法中各组观测值的权值。
| 类别 | 检查点数 | 特征点数 | 检查点均方差/m | 检查点最大残差/m | |||||
| X | Y | Z | X | Y | Z | ||||
| 传统后方交会法 | 6 | 4 | 0.125 | 0.194 | 0.242 | 0.286 | 0.221 | 0.573 | |
| 传统后方交会法 | 6 | 8 | 0.061 | 0.080 | 0.095 | 0.148 | 0.120 | 0.153 | |
| 本文方法 | 6 | 4 | 0.064 | 0.081 | 0.098 | 0.153 | 0.124 | 0.168 | |
| 影像 | 特征点 | 水平线 | 垂直线 | 水平圆 | 迭代次数 |
| 图 6(a) | 0.856 | 3.546 | 0.542 | 4.254 | 5 |
| 图 6(b) | 0.758 | 3.365 | 0.645 | 5.365 | 5 |
从表 3可以看出，传统后方交会法在特征点为4个时，计算获得的结果精度较低，检查点的均方差和最大残差都比较大，当特征点为8个时，计算获得的结果精度得到了明显的提高。而综合多种特征的后方交会法使用了4个特征点及3条水平线、3条垂直线与4个水平圆，检验结果与使用8个特征点的传统后方交会法精度相当。这说明了当特征点比较少时，利用多种特征进行后方交会计算能够在一定程度上提高计算结果的精度与稳定性，减少对特征点的依赖。
从表 4中可以看出：各组观测值在运算中的权值是不同的，水平圆的权值最大，其次是水平线，特征点的权值较小，垂直线的权值最小。这主要是由于水平线与水平圆的等量方程式(式(5)与式(17))包含了多个地面控制点，且水平线与水平圆在像平面上的观测值可以由多个特征点拟合而来，因此在平差运算中的残差较小，权值较大。而垂直线虽然也可以通过多个特征点来进行拟合，但是该试验数据是航空小倾角影像，图 6中楼房边缘的垂直线几何特征相对来说并不十分明显。另外，基于垂直线的等量方程式(式(7))仅包含像底点的像平面坐标，不包含地面控制点。因此，垂直线的观测值在平差运算中的残差最大，权值最小。
在实际的运用中，近景影像的外方位线元素初始值可以由相机安装的位置与高度尝试进行估计判断，外方位角元素中的φ、ω的初始值可由图像中心点所对应的地面点位置和相机位置的连线(即主光轴)估算得出，相机的云台一般是水平安装，所以κ的初始值可以设定为0°。航空影像的外方位线元素初始值可以由GPS等辅助手段获得，角元素可以设定为0°或者由航线朝向估算得出。另外，如果影像上存在3个以上的特征点，也可以先使用其他类型的后方交会方法获得影像外方位元素的初始值。
4 结 论本文详细论述了综合多种特征的后方交会法，该方法可以将水平线、垂直线、线段与水平圆等都纳入共线方程中进行联合平差，通过模拟数据与真实数据的后方交会对比试验，验证了该方法的有效性与实用性。它解决了特征点数不足时的后方交会问题，引入更多的观测值也能够保证后方交会计算结果的精度和可靠性，相对于传统的方法具有更强的优越性。但文中仅讨论了水平线、垂直线、线段与水平圆4种特征，对于一般意义上的直线与圆并未涉及，另外，本文的方法是基于共线方程改进而来的，对选取合适的初始值存在着一定的依赖，上述问题有待进一步研究解决，以增强该方法的普适性。
| [1] | WANG Zhizhuo. Principles of Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1979. (王之卓. 摄影测量原理[M]. 北京:测绘出版社,1979.) |
| [2] | JIN Weixian, YANG Xianhong, SHAO Hongchao, et al. Photogrammetry[M]. Wuhan: Wuhan University Press, 1996. (金为铣, 杨先宏, 邵鸿潮, 等. 摄影测量学[M]. 武汉:武汉大学出版社, 1996.) |
| [3] | GUAN Yunlan, ZHOU Shijian, ZHOU Ming, et al. Improved Algorithm of Spatial Resection Based on Pyramid[J]. Science of Surveying and Mapping, 2006, 31(2): 27-28. (官云兰, 周世健, 周铭, 等. 基于角锥体原理的空间后方交会改进算法[J]. 测绘科学, 2006, 31(2): 27-28.) |
| [4] | HARALICK B M, LEE C N, OTTENBERG K, et al. Review and Analysis of Solutions of the Three Point Perspective Pose Estimation Problem[J]. International Journal of Computer Vision, 1994, 13(3): 331-356. |
| [5] | HARTLEY R, ZISSERMAN A, EBRARY I. Multiple View Geometry in Computer Vision [M]. Cambridge: Cambridge University Press, 2003. |
| [6] | FENG Wenhao. Close Range Photogrammetry [M]. Wuhan: Wuhan University Press, 2002. (冯文灏. 近景摄影测量 [M]. 武汉: 武汉大学出版社, 2002.) |
| [7] | JIANG Gangwu, JIANG Ting, WANG Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2):169-175. (江刚武, 姜挺, 王勇, 等. 基于单位四元数的无初值依赖空间后方交会[J]. 测绘学报, 2007, 36(2): 169-175. ) |
| [8] | SHOEMAKE K. Animating Rotation with Quaternion Curves[J]. ACM SIGGRAPH Computer Graphics, 1985, 19(3): 245-254. |
| [9] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. A Globally Convergent Algorithm of Space Resection Based on Quaternion[J]. Acta Geodaetice et Cartographica Sinica, 2011, 40(5): 639-645.(龚辉, 姜挺, 江刚武, 等. 一种基于四元数的空间后方交会全局收敛方法[J]. 测绘学报, 2011, 40(5): 639-645.) |
| [10] | GUAN Yunlan, CHENG Xiaojun, ZHOU Shijian, et al. A Solution to Space Resection Based on Unit Quaternion [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 30-35.(官云兰, 程效军, 周世健, 等. 基于单位四元数的空间后方交会解算[J]. 测绘学报, 2008, 37(1): 30-35.) |
| [11] | ZHANG Zuxun, ZHANG Jianqing. Generalized Point Photogrammetry and Its Application[J]. Geomatics and Information Science of Wuhan University , 2005, 30(1): 1-5. (张祖勋, 张剑清. 广义点摄影测量及其应用[J]. 武汉大学学报: 信息科学版, 2005, 30(1): 1-5.) |
| [12] | ZHANG Zuxun, ZHANG Yong. Study of the Vertical Lines Supported Aerial Triangulation over Urban Areas[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 659-662.(张祖勋, 张勇. 城区铅垂线辅助空中三角测量研究[J]. 武汉大学学报: 信息科学版, 2007, 32(8): 659-662.) |
| [13] | ZHANG Jianqing, ZHANG Yong, FANG Fang. Absolute Orientation of Aerial Imagery over Urban Areas Combined with Vertical Lines [J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 197-200.(张剑清, 张勇, 方芳. 铅垂线辅助城区航空影像的绝对定向 [J]. 武汉大学学报: 信息科学版, 2007, 32(3): 197-200.) |
| [14] | ZHANG Yongjun, HU Binghua, ZHANG Jianqing. Relative Orientation Based on Multiple Conjugate Features [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 194-199.(张永军, 胡丙华, 张剑清. 基于多种同名特征的相对定向方法研究 [J]. 测绘学报, 2011, 40(2): 194-199.) |
| [15] | ZHANG Y, HU B, ZHANG J. Relative Orientation Based on Multi-features[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5): 700-707. |
| [16] | ZHANG Yongjun. Reconstruction of Circles and Round Rectangles by Generalized Point Photogrammetry[J]. Journal of Harbin Institute of Technology, 2008, 40(1): 36-39.(张永军. 基于广义点摄影测量的圆和圆角矩形三维重建[J]. 哈尔滨工业大学学报, 2008, 40(1): 36-39.) |
| [17] | ZHENG Shunyi, GUO Baoyun, LI Cailin. 3D Reconstruction and Inspection of Cylinder Based on Geometric Model and Generalized Point Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 477-482.(郑顺义, 郭宝云, 李彩林. 基于模型和广义点摄影测量的圆柱体自动三维重建与检测[J]. 测绘学报, 2011, 40(4): 477-482.) |
| [18] | TANG Min, ZHANG Zuxun, ZHANG Jianqing. 3D Reconstruction and Inspection of Industrial Sheet Metal Parts with Multiple Baseline Images Based on Generalized Point Photogrammetry Theory[J]. Geomatics and Information Science of Wuhan University, 2007, 32(12): 1095-1098.(唐敏, 张祖勋, 张剑清. 基于广义点理论的多基线影像钣金件3D重建与尺寸检测[J]. 武汉大学学报: 信息科学版, 2007, 32(12): 1095-1098.) |
| [19] | SUI Lifeng, SONG Lijian, CHAI Hongzhou. Error Theory and Measurement Adjustment Basis[M]. Beijing: Surveying and Mapping Press, 2010.(隋立芬, 宋力杰, 柴洪洲. 误差理论与测量平差基础 [M]. 北京:测绘出版社, 2010.) |
| [20] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002.(李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002. ) |