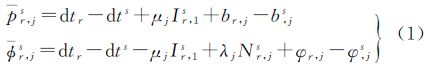1 引 言
联合处理多参考站的GNSS数据,可服务高精度大地测量。数据处理模式包括双差基线解(简称“DD模式”)和非差精密单点定位解(简称“PPP模式”)两种策略。基于全球参考站网,各IGS(international GNSS service)分析中心采用DD模式确定卫星轨道[1, 2],而采用PPP模式估计卫星钟差[3]。上述各类产品已广泛应用于授时和导航等领域[4, 5]。此外,广域/局域GNSS参考网数据处理,还是实现广域差分[6]、大气延迟提取[7]、形变监测[8, 9]和实时动态定位(RTK)[10]等技术的前提。
DD模式与PPP模式各有利弊。DD模式下,通过最优独立基线选取,可确定一组整周相位模糊度[11]。经由模糊度固定,其余参数的估计精度将得到改善[12]。然而,独立基线选取易受共视卫星个数、基线长度等因素的限制,影响了观测数据利用效率;PPP模式下,基本观测量为消电离层组合观测值,摆脱了对卫星需共视的要求,更充分地利用了观测数据[3, 4]。然而,由于吸收了接收机和卫星相位偏差,可估模糊度一般为实数,网解参数的可靠性将由此受到影响[13]。
通过S-基准变换和消秩亏理论[14],文献[15]推导了基于非差观测值的GNSS参考网数据处理模型:一方面,相位偏差参数被当作时变参数,并与钟差参数进行了合并;另一方面,通过定义一组基准模糊度,消除了模糊度与钟差参数的线性相关,并确保了剩余可估模糊度的整周特性。这两方面因素致使所导出的非差模型与DD模式具备完全等价性[15]。针对PPP模式,文献[12]对其实施了改进:首先,将实数解的非差模糊度映射成双差模糊度,以便于发掘模糊度的整周特性;随后,实施整周模糊度固定,以改善网解的可靠性。
依照文献[15]所提供的思路,基于非差、非组合的GNSS参考网观测值,通过选取两组基准参数,本文分别推导了对应于DD和PPP模式的满秩观测方程,以此为基础,对比分析了两种模式的特点和不足。随后,借鉴文献[12]中的算法思想,在综合考虑相位偏差的时不变性、双差模糊度的整周性基础上,提出一种基准参数的精选方案,实现了新的参考网数据处理策略。其优点包括:①相位偏差独立可估,其时间稳定性可在参数估计中加以考虑[16];②既有效利用了所有观测信息,又确保了可估模糊度的整数性。
2 非差网观测方程消秩亏从GNSS非差、非组合观测值出发,推导了对应于DD和PPP模式的列满秩观测方程。为了简化推导,本节假定测站和卫星位置,对流层延迟等无法引起秩亏的几何参数已知。而在实际中,当该假设不成立时,则还需在观测方程中引入未知的几何参数(如本文随后算例),但这并不会引起额外的列秩亏,更不会影响本节所导出的满秩模型和相关结论的适用性。
2.1 GNSS观测方程GNSS伪距和相位方程分别为[17]
式中,pr,js和Φr,js为测站r至卫星s第j个频率的伪距、相位观测值,几何参数均已事先改正,单位为m;dtr、br,j和φr,j分别为接收机的钟差、伪距偏差以及相位偏差参数;dts、b,js和φ,js则为对应的卫星参数;Nr,js为非差整周模糊度;Ir,1s 表示L1频率电离层群延迟;μj=λj2/λ12,λj表示频率j相位观测值的波长。除Nr,js单位为周外,式(1)中其余参数的单位均为m。若实施多历元数据处理,还需考虑各类参数的时变特性:例如,钟差历元间变化较大,需每历元估计一组新参数;伪距和相位偏差、模糊度等随时间变化极为缓慢,通常被模型化为时不变参数等。
若某历元时刻,构成参考网的n个测站(r=1,2,…,n)同步观测到m颗共视卫星(s=1,2,…,m)的双频观测值(j=1,2),式(1)设计矩阵的零空间维数,即列秩亏个数为4(n+m)+1[18]。为确保参数可估性,须将一部分参数约束为“基准”以消除秩亏,并遵循如下准则:①凡构成设计矩阵零空间的子矩阵,其对应的一组未知参数均可被选取为基准;②基准参数的个数须与秩亏数相等;③基准参数的取值可任意假定,但一般设为零值。
2.2 消秩亏策略Ⅰ:DD模式DD模式下的消秩亏步骤和基准选取原则可简述如下:
(1) 将n+m个dtr和dts选取为基准,消除钟差与伪距和相位偏差的相关性。
(2) 将4个φ1,j和b1,j选取为基准,消除卫星和接收机偏差之间的相关性。
(3) 将n+m-1个φ,1s和φi,1(i≠1)选取为基准,消除电离层和相位偏差之间的相关性。
(4) 将2(n+m-1)个λjNp,jq(p=1∨q=1)选取为基准,消除相位偏差和模糊度之间的相关性,其中∨表示并集运算符。
表 1第1列列举了DD模式下所选取的基准参数,第2列给出了可估参数,主要包括(由上到下):(第2个频率的)接收机和卫星相位偏差,双频的接收机和卫星伪距偏差、电离层以及模糊度参数。值得注意的是,所有可估参数均包含了基准参数,其物理含义与式(1)中的对应项有所不同。
| 基准参数 | 可估参数 |
| dtr、dts φ1,j、b1,j φ,1s、φi,1 i≠1 λjNp,jq p=1∨q=1 |
Δφi1,2-λ2ΔN1i,21-μ2(Δφi1,1-λ1ΔN1i,11)+(1-μ2)Δdti1 i≠1 φ,2s-b1,2-λ2N1,2s+(1-μ2)(dts-dt1)-μ2(φ,1s-b1,1-λ1N1,1s) Δbi1,j+μj(Δφi1,1-λ1ΔN1i,11)+(1+μj)Δdti1 i≠1 b,js-b1,j+μj(φ,1s-φ1,1-λ1N1,1s)+(1+μj)(dts-dt1)  λj(Np,jq-Np,j1-N1,jq+N1,j1) p≠1∧q≠1 |
| 注:Δ为站间单差运算符,如Δζab=ζa-ζb;∧为交集运算符 | |
考察DD模式下可估参数,可得几点结论:首先,模糊度参数具备双差形式和整数特性,经由整周模糊度解算,可有效改善其余参数的估计精度和可靠性;但另一方面,伪距和相位偏差中均吸收了钟差参数,致使其随时变性受不稳定的钟差变化支配。这就意味着,在多历元数据处理中,该类偏差的时变模型将“不得不”选取为白噪声过程,进而导致待估参数个数的增加(详见后文算例)。
2.3 消秩亏策略Ⅱ:PPP模式类似的,PPP模式下消秩亏步骤和基准参数选取原则为:
(1) 将2(n+m)个br,j和b,js选取为基准,消除伪距偏差和钟差以及电离层间的相关性。
(2) 将2(n+m)个φr,j和φ,js选取为基准,消除相位偏差和模糊度之间的相关性。
(3) 将1个dt1选取为基准,消除接收机和卫星钟差之间的相关性。
表 2中列举了PPP模式下的基准参数和可估参数的形式,其中后者主要包括(从上到下):接收机和卫星钟差、电离层和模糊度参数。与表 1对比可知,由于基准参数选取的差异,两种模式下可估参数的含义发生变化,主要表现为两个方面:首先,前文已述,由于将钟差选取为基准,DD模式下相位偏差独立可估,但时不变性受到影响,而PPP模式下,相位偏差选为基准,进而被模糊度吸收,有效保留了其时间稳定性;其次,为消除模糊度和相位偏差之间的线性相关,DD和PPP模式分别选取部分模糊度和相位偏差作为基准,致使两种模式下的可估模糊度分别保留和丧失了整数特性。
| 基准参数 | 可估参数 |
| br,j、b,js φr,j、φ,js dt1 |
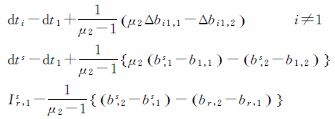 λjNr,js+(φr,j-φ,js)-{r2(br,j1-b,1s)-r1(br,2-b,2s)} |
| 注:γl=(μj+μl)/(μ2-1),l=1,2 | |
针对上述两种模式下,选取不同基准所引起待估参数的特性变化,提出一种新的基准参数选取策略,同时顾及了模糊度的整数特性和相位偏差参数的时间稳定性。具体的消秩亏模式可简述为:
(1) 将2(n+m)个br,j和b,js选取为基准,消除伪距偏差和钟差以及电离层间的相关性。
(2) 将2个φ1,j选取为基准,消除卫星和接收机相位偏差偏差间的相关性。
(3) 将1个dt1选取为基准,消除接收机和卫星钟差之间的相关性。
(4) 将2(n+m-1)个λj·Np,jq(p=1∨q=1)选取为基准,消除相位偏差和模糊度之间的相关性。
与DD和PPP模式下的消秩亏过程相比,新模式的特性包括:①借鉴PPP模式,将偏差参数选取为基准,保留了可估相位偏差的时不变性;②借鉴DD模式,将部分模糊度选取为基准,使得可估模糊度具有整数特性。因此,新模式融合了DD和PPP模式的优点,进而在多历元数据处理中,可发掘更多的有用信息,以增强参数解的可靠性。值得注意的是,在估计浮点模糊度的条件下,新模式和PPP模式下的时不变参数个数相同,且存在一一对应的转换关系,故两种模式下,各类参数的模糊度浮点解等价。表 3中给出了新模式下可估参数的具体形式,由上到下分别为:接收机和卫星钟差、(双频的)接收机和卫星相位偏差、电离层和模糊度参数。
| 基准参数 | 可估参数 |
| br,j、b,js φ1,j dt1 λjNp,jq p=1∨q=1 |
 ΔΦi1,j-λjΔN1i,j1+γ1Δbi1,2-γ2Δbi1,1 i≠1 Φ,js-Φ1,j-λjN1,js+γ1(b,2s-b1,2)-γ2(b,1s-b1,1) 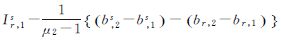 λj(Np,jq-Np,j1-N1,jq+N1,j1) p≠1∧q≠1 |
试验基于某4个测站在2009-08-08采集的双频GPS观测值(L1-L2-C1-P2),采样间隔为15s。各测站的空间分布、DD模式下的独立基线和长度等如图 1所示。设计4种网数据处理模式(均采用动态基线解算):S1-DD模式,浮点模糊度解;S2-DD模式,整数模糊度解;S3-PPP模式;S4-新模式,整数模糊度解,以便于单独考察相位偏差时变模型选取、整周模糊度固定对位置解的影响。试验选取的测站均是某省级连续运行参考系统的参考站,其先验坐标精度优于1cm,将用作S1-S4模式下解算的参考值。试验还采用了IGS精密卫星轨道和钟差产品,以尽可能地降低星历误差的影响。

|
| 图 1 试验所采用的4测站参考网 Fig. 1 The 4-station reference network used in the experiment |
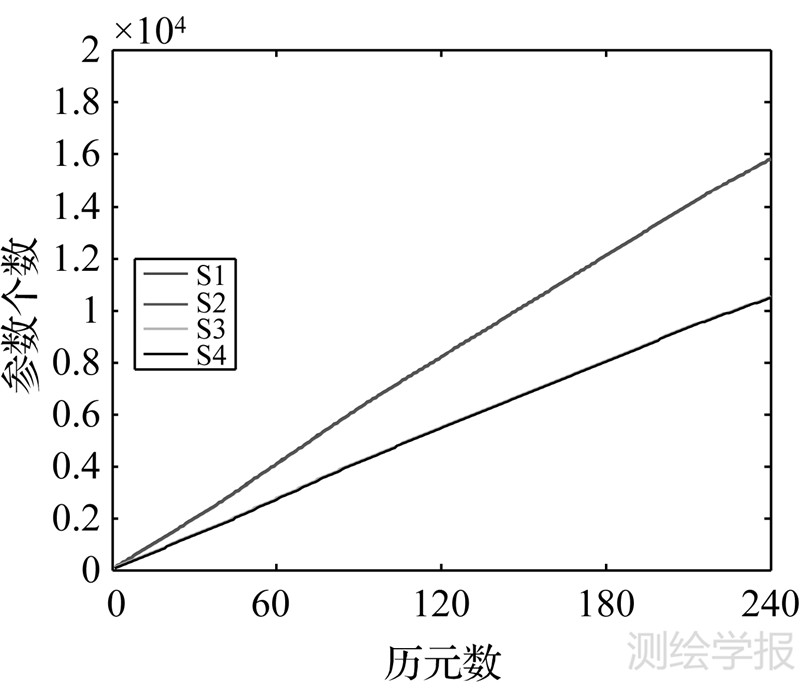
假定某观测时段共包含t个历元,且不存在卫星的升降变化,上述4种模式下的时变和时不变参数个数随历元数变化如表 4所示。基于1h的上述试验数据,图 2中由上而下绘出了4条直线,依次对应4种模式下参数总数随时间变化规律。显见,S1和S2模式下总的参数个数随历元迅速增加,1h后均接近16000个。但由于整周模糊度解算,S2模型的参数个数略少于S1;而在S3和S4模式中,由于考虑了相位偏差的时间稳定性,1h后参数总数仅为8000个。因此,通过解算整周模糊度和约束相位偏差,可以显著地减少待估参数,提高相应的模型强度。
| 网处理模式 | 时变参数个数 | 时不变参数个数 |
| S1 | t[3(n+m-1)+nm] | 2(n-1)(m-1) |
| S2 | t[3(n+m-1)+nm] | 0 |
| S3 | t(n+m-1+nm) | 2nm |
| S4 | t(n+m-1+nm) | 2(n+m-1) |
|
| 图 2 4种模式下参数个数随历元变化(1h内) Fig. 2 The numbers of unknown parameters versus the epochs for four schemes (in 1h) |
试验的参数估计策略可概括为:①基于正、反向卡尔曼滤波,仿动态求解各历元基线分量的全局最优解;②待估参数包括基线分量(白噪声过程)、天顶对流层延迟(批参数,每2h估计一组)、模糊度(时不变)、相位偏差(S1和S2模式,白噪声过程;S3和S4模式,时不变)、钟差(仅S3和S4模式,白噪声过程);③观测值的截止高度角为15°,伪距和相位观测值的先验中误差选为3dm和3mm;④S2和S4模式中,采用LAMBDA和固定失败率的FFRatio实施模糊度固定和有效性检验[19, 20]。
特别的,S1-S2模式下,电离层参数包含时变的接收机钟差基准,失去短期内平稳变化的特性;而S3-S4模式下,电离层参数吸收稳定的伪距偏差基准,其时变性未受影响,可因此对其引入适当的动态模型[21, 22]。在试验中,为便于考察相位偏差和模糊度固定对基线解的影响,S1-S4模式下的电离层参数均统一地模型化为白噪声过程。
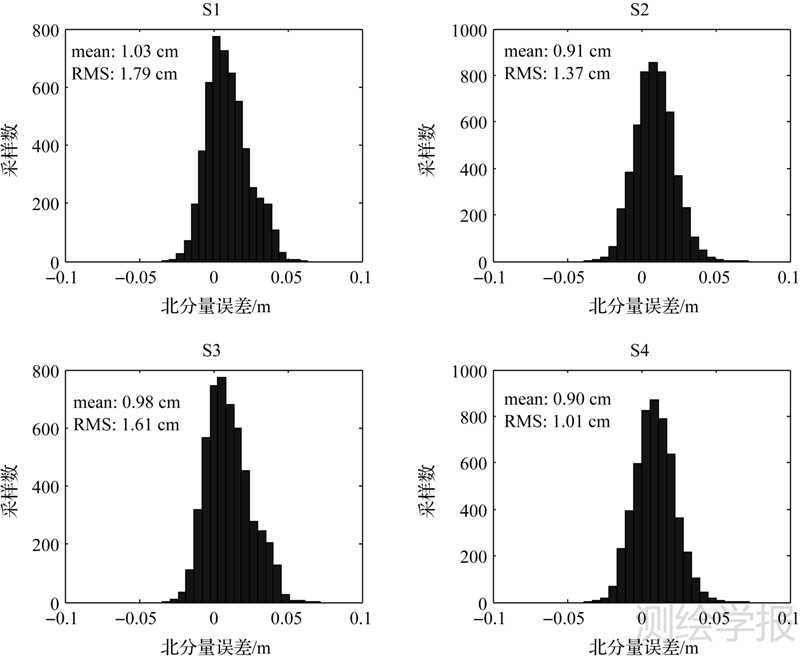
以基线TSLT-TSZH为例,分析了4种模式下的三维(北、东和天顶)基线解误差(单位:m)及其两类统计量:均值和RMS(单位:cm)。可得到如下结论(图 3中仅绘出北分量误差,以节约篇幅):
|
| 图 3 4种模式下,基线TSLT-TSZH的北分量误差 (动态解) Fig. 3 The north component errors of baseline TSLT-TSZH (kinematic solution) in four schemes |
(1) 模糊度固定之前,S3模式下的三维基线解误差RMS分别为1.61cm、1.46cm和5.30cm。较之S1的北、东和天顶基线分量RMS改善可分别达10%、8.8%和1.7%;模糊度固定之后,S4模式下的三维基线解误差RMS则分别为1.01cm、0.93cm和3.26cm,较之S2模式的三维基线分量改善则分别为26%、24%和24.2%。相位偏差的不同时变模型是上述RMS差异的主因,且对基线分量固定解的影响远大于浮点解。
(2) 对比S2和S1模式的位置解可知,DD模式下,整周模糊度固定对三维基线分量RMS改善程度分别为23.4%、21.8%和20.2%;而通过比较S4和S3模式可知,新模式下,模糊度固定所引起的基线分量改善则分别为37.3%、36.3%和38.5%。后两种模式中,由于对相位偏差的历元间变化施加了合理的约束,在减少待估参数个数的同时,增强了模型的可靠性,此时,整周模糊度固定更加明显地改善了基线解。
(3) S4较之S1模式位置解的精度改善,源于相位偏差的时变模型选取和整周模糊度固定的综合作用,3分量上分别为43.6%、41.9%和39.5%。
总之,通过分析RMS指标,上述试验方案量化了S1-S4模式下,不同的模型假设对动态基线分量解的影响。另一方面,若在解算静态基线的条件下重复该试验,前述若干量化性的结论(如不同模式之间,RMS改善量级等)将发生改变,但有关不同模式优劣的结论(如S4模式下,RMS改善最显著)将依然成立。
4 总结和展望目前,GNSS参考站网数据处理模式包括两种:基于双差观测值的DD模式和基于非差观测值的PPP模式。本文从秩亏的非差GNSS观测方程出发,选取两组基准参数消秩亏,导出了分别对应于DD和PPP模式的满秩函数模型。随后,归纳了两种模式下,各类待估参数的具体形式和时变特性。分析表明,DD模式和PPP模式分别顾及了模糊度的整数性和相位偏差的时间稳定性。通过精选另一组基准参数,本文推导了一种参考网数据处理模式。该模式同时发掘了相位偏差的稳定性和模糊度的整数性条件,因此保留了DD和PPP模式的优势,并回避了各自的不足。基于某4测站的实测GPS双频数据,通过设计不同的参考网数据处理方案,考察了相位偏差动态模型或(和)整周模糊度固定对北、东和天顶基线分量仿动态解的影响,证实了该模式能提供较DD和PPP模型更为可靠的结果。
针对基于局域参考网的网络RTK技术,本文模式能估计非差形式的大气延迟。与双差大气延迟相比,内插非差大气延迟将不再受参考测站(卫星)的影响,用户站处改正信息的生成将更为简单、直观;针对基于广域参考网的PPP-RTK技术,本文模式能提供基准一致的卫星相位偏差、卫星钟差等,以用作实现单站PPP模糊度固定所必须的改正信息。
| [1] | DOW J, NEILAN R, RIZOS C. The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems[J]. Journal of Geodesy, 2009, 83(3-4): 191-198. |
| [2] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines Up to 2000km[J]. Journal of Geophysical Research, 1989, 94(B8): 10187-10203. |
| [3] | ZUMBERGE J, HEFLIN M, JEFFERSON D, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102: 5005-5017. |
| [4] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning (PPP) Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478-483. (张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39 (5): 478-483.) |
| [5] | TEUNISSEN P J G, ODIJK D, ZHANG B C. PPP-RTK: Results of CORS Network-based PPP with Integer Ambiguity Resolution[J]. Journal of Aeronautics, Astronautics and Aviation: Series A, 2010, 42(4): 223-230. |
| [6] | WUEBBENA G, SCHMITZ M, BAGGE A. PPP-RTK: Precise Point Positioning Using State-space Representation in RTK Networks[C]//Proceedings of the ION GNSS 2005, Long Beach: [s. n.], 2005: 2584-2594. |
| [7] | YUAN Y B, TSCHERNING C C, KNUDSEN P. The Ionospheric Eclipse Factor Method (IEFM) and Its Application to Determining the Ionospheric Delay for GPS[J]. Journal of Geodesy, 2008, 82(1): 1-8. |
| [8] | HAMMOND W C, BLEWITT G, KREEMER C. Block Modeling of Crustal Deformation of the Northern Walker Lane and Basin and Range from GPS Velocities[J]. Journal of Geophysical Research: Solid Earth, 2011, 116 (B4): 10-37. |
| [9] | GAGNON K, CHADWELL C, NORABUENA E. Measuring the Onset of Locking in the Peru-Chile Trench with GPS and Acoustic Measurements[J]. Nature, 2005, 434(3): 205-208. |
| [10] | ZHANG B C. Determination of Un-differenced Atmospheric Delays for Network-based RTK [C]//Proceedings of Institute of Navigation GNSS 2009. Savannah: [s. n.], 2009: 2727-2738. |
| [11] | BOCK Y, ABBOT R, COUNSELMAN Ⅲ C, et al. Establishment of Three-dimensional Geodetic Control by Interferometry with the Global Positioning System[J]. Journal of Geophysical Research: Solid Earth, 1985, 90(B9): 7689-7703. |
| [12] | BLEWITT G. Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing: Ambizap[J]. Journal of Geophysical Research, 2008, 113(B12): 7689-7703. |
| [13] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135-149. |
| [14] | TEUNISSEN P J G. Generalized Inverses, Adjustment, the Datum Problem and S-transformations[C]//Optimization and Design of Geodetic Networks. Berlin: Springer, 1985: 11-55. |
| [15] | JONGE P J D. A Processing Strategy for the Application of the GPS in Networks [M]. Amsterdam: NCG Nederlandse Commissie voor Geodesie, 1998: 37-59. |
| [16] | OU Jikun. Uniform Expression of Solutions of Ill-posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 283-288. (欧吉坤. 测量平差中不适定问题解的统一表达与选权拟合法[J]. 测绘学报, 2004, 33(4): 283-288.) |
| [17] | TEUNISSEN P J G, KLEUBERG A. GPS for Geodesy [M]. 2nd ed. Berlin: Springer, 1998: 188-194. |
| [18] | LANNES A, TEUNISSEN P J G. GNSS Algebraic Structure[J]. Journal of Geodesy, 2011, 85(5): 273-290. |
| [19] | TEUNISSEN P J G. The Least-square Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Resolution[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |
| [20] | TEUNISSEN P J G, VERHAGEN S. The GNSS Ambiguity Ratio-test Revisited: A Better Way of Using It[J]. Survey Review, 2009, 41(312): 138-151. |
| [21] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver’s Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40 (4): 446-453. (张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40 (4): 446-453.) |
| [22] | ZHANG Baocheng, OU Jikun. On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40 (6): 710-716. (张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40 (6): 710-716.) |