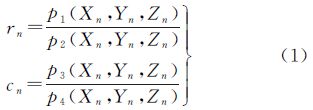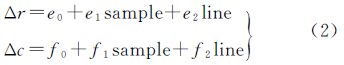2. 国家测绘地理信息局 卫星测绘应用中心,北京 100830;
3. 湖南省测绘科技研究所,湖南 长沙 410018
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 100083, China;
3. Hunan Provincial Mapping and Science and Technology Investigation Insitute, Changsha 410018, China
随着第一颗民用高分辨率立体测绘卫星资源三号的发射,我国的高分辨率对地观测能力正在逐步增强[1, 2]。卫星影像的区域网平差技术是卫星影像稀少控制点条件下精确几何定位的一种重要手段,区域网平差的精度直接决定了后续测绘生产产品的精度。国家测绘地理信息局启动的地理国情监测项目中明确提出了“要建成全国范围1∶50 000比例尺,重点区域优于1∶10 000比例尺的地表三维立体系统,形成二、三维一体化、高精度、全覆盖、空间连续的全国地理国情一张图”。作为地理国情监测最重要的数据源——高分辨率卫星遥感影像,首先要解决的核心问题是卫星遥感影像区域网平差所解算的影像定向精度。目前,卫星影像区域网平差方式都是基于影像间重叠区域内同名光线对对相交这一基本光线交会的原理来构建区域网,且在具有良好的几何交会条件下进行的立体区域网平差,对此国内外的很多专家学者都进行了大量研究。
在利用严密成像几何模型进行卫星影像立体区域网平差方面,文献[3]提出了PPM(piecewise polynomial model)模型并将其应用在TLS和MOMS-02影像的区域网平差,取得了子像素级的精度。文献[4]针对VIR和SAR影像的多源遥感影像联合平差,有效地合并了严密成像几何模型中的强相关项,提出了TM(Toutins model)模型,亦取得了很好的效果。文献[5]将扩展共线方程和定向片模型分别成功地应用于SPOT-5和MOMS-02影像。文献[6]根据EFP(equivalent frame photo)原理提出了卫星遥感三线阵CCD影像光束法平差的控制方案和CCD相机的改善措施。文献[7]提出了针对长条带卫星遥感影像的区域网平差方法。就利用通用几何模型进行卫星遥感影像区域网平差而言,最具代表性的通用几何模型为有理函数模型(rational function model,RFM)[8]。RFM模型是对严密成像几何模型的高精度近似,可以适用于任意航天传感器平台。文献[9]将其应用于IKONOS影像的区域网平差,取得了平面和高程均优于±1像素的定位精度。文献[10]在进行IKONOS影像的区域网平差研究中,证明了RFM模型比严密几何模型更加稳定,并且在精度上能够达到一致的水平。文献[11]将RFM模型用于SPOT-5 HRS立体影像对的平差,在缺少控制点情况下得到了很好的平差精度。文献[12]将RFM模型应用于SPOT-5 HRS立体影像的区域网平差,仅用少量控制点就可满足我国西部1∶50 000地形图测绘的要求。文献[13]利用RFM模型对资源三号卫星影像进行立体平差,在四角布控方案下获得了平面3.2 m、高程1.8 m的精度。
以上的研究均是在卫星影像具有良好的交会条件下进行的。但是,地理国情监测以及国土二调等项目中的需求是进行大区域影像的正射纠正以及保障纠正后正射影像间的拼接精度。在该方面,如果已经有该区域的DEM,一般采用正视影像进行正射纠正并基于此影像进行拼接。在这种情况下,参与纠正处理的卫星影像重叠区域均较小且交会角也非常之小(一般情况下小于10°),难以构成立体影像对,即呈现弱交会状态。在这种情况下,针对良好交会条件下的卫星影像立体区域网平差方法无法满足精度需求。
基于大区域正射纠正中所遇到的实际问题出发,本文提出了弱交会条件下卫星影像平面区域网平差的方法,推导了卫星影像平面区域网平差的误差方程,设计了平面区域网平差的解算流程。在此基础上,为了验证本文所提出平面区域网平差方案的有效性和可行性,采用资源三号三线阵全色影像中的正视影像和三线阵影像进行区域网平差试验。试验结果证明了本文所提出的卫星影像平面区域网平差可以达到与立体区域网平差相当的平面精度。
2 弱交会条件下平面区域网平差的基本原理 2.1 卫星影像平面区域网平差的数学模型考虑到卫星拍摄时的长焦距和窄视场角导致近似平行投影的特点,在基于严密几何成像模型的卫星影像区域网平差时会造成定向参数之间存在很强的相关性。因而,利用严密几何成像模型处理高分辨率卫星影像虽然在理论上严密,但其优越性却往往被求解参数众多、数值解算不稳定等缺点所淹没[12]。文献[10, 13]的研究表明利用RFM进行卫星影像的区域网平差,其精度能够达到基于严密几何模型的区域网平差精度。再加之RFM具有形式简单和计算速度快等优势,综上所述,平面平差选择RFM作为平差的几何处理模型。
RFM是将像点坐标(r,c)表示为含地面点坐标(X,Y,Z)的多项式的比值[7, 14],一般形式为
式中,多项式pi (i=1,2,3,4)中每一项的各个坐标分量Xn、 Yn、 Zn的幂次及其幂之和最大不超过3。 2.2 弱交会条件下的平面区域网平差参与区域网平差的卫星影像间交会角较小(小于10°)时,一般称之为弱交会条件。此时,若采用传统的卫星影像平差方式会造成平差结果不收敛、连接点处高程求解异常等问题。针对这个问题,笔者对弱交会条件下卫星影像的平面平差进行了深入的研究。卫星影像的平面平差是指在区域网平差过程中不求解连接点地面坐标的高程值,仅计算卫星影像的定向参数和连接点物方平面坐标的一种区域网平差方式[15],这种平差方式可以保证平差解算的稳定以及平差后物方点平面坐标的精度。与基于RFM的立体区域网平差类似,平面区域网平差并不改正RPC参数(rational polynomial coefficients,RPCs),而是仅仅改正RPC模型的系统误差补偿参数。RPC模型的系统误差补偿模式可以分为物方补偿和像方补偿两种方案[16]。研究表明,基于像方补偿方案能够很好地消除影像的系统误差[17],从而提高基于RFM的影像几何处理精度。
基于像方的系统误差补偿模型中最为常用的是仿射变换模型,即6个未知数,最少需要3个控制点进行参数求解。利用一个控制点可以求解偏移参数,即e0和f0,这样几乎可以吸收大部分的误差。利用两个控制点即可同时求解平移和漂移(由于陀螺随时间漂移等引起)量
式中,line和sample为由RFM计算得到的影像坐标;(e0,e1,e2)和(f0,f1,f2)为仿射变换系数;Δr、Δc为像方改正值[18]。在式(1)和式(2)的基础上,将像方补偿的仿射项参数(e0,e1,e2)和(f0,f1,f2)作为未知数与地面点平面坐标(X,Y)等未知数一并求解,即得到基于RFM模型的区域网平差误差方程式
式中,ΔX、ΔY为待定点的地面坐标改正数。在每次平差结束之后得到连接点新的物方平面坐标,此时加入数字高程模型DEM作为高程约束,在连接点处通过DEM内插该点的地面点坐标高程值Z(而非通过多片前方交会得到),将其与平面坐标(X,Y)一起代入平差系统中进行下一次迭代计算,直到整个平差过程收敛。
3 试验结果与分析 3.1 试验数据笔者采用经过几何检校的[19]资源三号测绘卫星的传感器校正产品[20]作为试验数据,包含影像和RPC参数。
采用两个试验区数据,分别为黑龙江省的齐齐哈尔测区和陕西省的渭南测区。齐齐哈尔测区范围为122.107°E—124.614°E,45.082°N—48.723°N,试验区的地貌包括平原和山地,平原为主,高程范围130~300 m。该测区共有5轨数据,每轨分别含有1景前、后、正视全色影像,共15幅影像。其中有2景是长条带影像数据(沿轨方向分别为2、3个标准景),该测区的内设置了73个均匀分布的控制点。
陕西渭南测区范围为107.738°E —109.335°E和33.983°N —35.316°N。试验区地势南北高,中间低,东西开阔。按地表形态可粗分为山地、平原两大土地类型,平原为主。该测区共有3轨数据,每轨分别含有3景前、后、正视全色影像,共27幅影像。该测区同样采用人工量测的方式刺了52个控制点。
试验区基本参数如表 1所示。
| 项目 | 齐齐哈尔5×1试验区 | 渭南3×3试验区 |
| 正视影像分辨率 /m | 2.1 | 2.1 |
| 前后视影像分辨率/m | 3.5×3.7 | 3.5×3.7 |
| 轨道数/条 | 5 | 3 |
| 控制点/个 | 73 | 52 |
| 连接点/个 | 62 | 28 |
| 最大地形起伏/m | 300(平原和山地) | 767(平原和山地) |
所有在影像上量测的控制点均为明显地物点,如道路交叉口、房屋拐角点等,通过人工比对控制影像和资源三号卫星影像上的同名点得到。控制影像满足1∶10 000国家基础测绘生产成果的精度,平面位置精度为±5 m,高程值是通过1∶50 000 DEM内插获得的。但是本测区控制点片对应的影像分辨率差异较大,这对于资源三号卫星2.1 m的分辨率会导致控制点不易识别(高分辨率影像上的地物在资源三号卫星影像上对应的位置较难准确找到),且部分控制点布设在围墙角、房顶等起伏较大区域,刺点精度在±1个像素甚至更低。图 1中左影像为1∶10 000测图的控制影像,其影像上可识别地物远远多于资源三号影像(右影像)上的地物,这种分辨率不一致给控制点的像点坐标量测带来了一定的精度损失。

|
| 图 1 控制点在控制影像与资源三号影像上对比 Fig. 1 Comparison of GCP in the control image and ZY-3 image |
为了比较和验证资源三号影像的平面区域网平差和立体区域网平差的精度差异,以及不同精度的DEM对平面区域网平差精度的影响,每个试验区域在同一套控制数据和同一套检查数据的保障下,主要采用以下几种方案进行对比试验:
试验1:平面区域网平差与立体区域网平差对比试验,平面区域网平差采用1∶50 000 DEM作为高程约束,格网大小是25 m×25 m。该试验目的是为了验证弱交会条件下的平面区域网平差和立体区域网平差所能达到的平面精度。
方案1:仅采用资源三号卫星的正视影像进行无控制点的自由网平面区域网平差,所有的控制点都作为独立检查点。
方案2:仅采用资源三号卫星的正视影像进行带控制点的区域网平面区域网平差,在区域中均匀分布稀少的控制点,其余控制点作为独立检查点。
方案3:采用资源三号卫星的前正后视影像进行无控制点的自由网立体区域网平差,所有的控制点都作为独立检查点。
方案4:采用资源三号卫星的前正后视影像进行带控制点的区域网立体区域网平差,在区域中均匀分布稀少的控制点,其余控制点作为独立检查点。
试验2:验证不同DEM精度对平差区域网精度的影响。该试验仅采用资源三号正视影像,其目的是为了验证平面平差所需要DEM的精度,以及DEM精度对最终平面平差精度的影响。
方案1:采用全球SRTM作为高程控制,格网大小是90 m×90 m,无控制点的自由网平面平差。
方案2:采用全球SRTM作为高程控制,格网大小是90 m×90 m,带控制点的控制网平面平差。
方案3:采用全球DEM作为高程控制,格网大小是1000 m×1000 m,无控制点的自由网平面平差。
方案4:采用全球DEM作为高程控制,格网大小是1000 m×1000 m,带控制点的控制网平面平差。
3.3 立体与平面区域网平差对比试验采用3.2节所设计的试验方案,进行了资源三号立体和平面区域网平差的对比试验,依据检查点统计的结果列于表 2。
| 试验区 | 平差类型 | 平差方案 | 控制点/个 | 检查点/个 | 最大残差/m | 中误差/m | |||||||
| E | N | 平面 | 高程 | E | N | 平面 | 高程 | ||||||
| 齐齐哈尔 | 立体平差 | 无控平差 | 0 | 73 | 20.516 | 9.817 | 22.585 | 16.048 | 8.748 | 5.125 | 10.139 | 6.400 | |
| 带控平差 | 12 | 61 | 7.531 | 8.125 | 8.319 | 7.911 | 2.806 | 3.172 | 4.235 | 3.366 | |||
| 平面平差 | 无控平差 | 0 | 73 | 25.122 | 8.843 | 26.287 | - | 10.970 | 3.598 | 11.545 | - | ||
| 带控平差 | 12 | 61 | 6.710 | 8.781 | 9.134 | - | 2.837 | 3.136 | 4.229 | - | |||
| 陕西渭南 | 立体平差 | 无控平差 | 0 | 52 | 13.315 | 15.689 | 18.865 | 20.759 | 9.282 | 10.252 | 13.830 | 13.902 | |
| 带控平差 | 9 | 43 | 6.218 | 7.130 | 7.159 | 6.861 | 3.317 | 2.967 | 4.450 | 2.622 | |||
| 平面平差 | 无控平差 | 0 | 52 | 15.154 | 18.304 | 20.130 | - | 9.478 | 9.429 | 13.370 | - | ||
| 带控平差 | 9 | 43 | 6.049 | 7.227 | 7.425 | - | 2.523 | 2.999 | 3.919 | - | |||
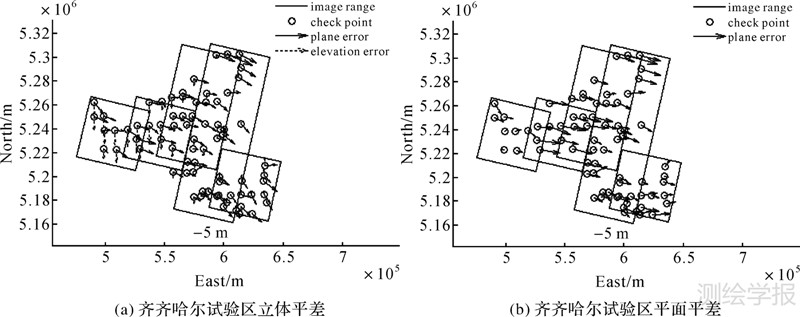
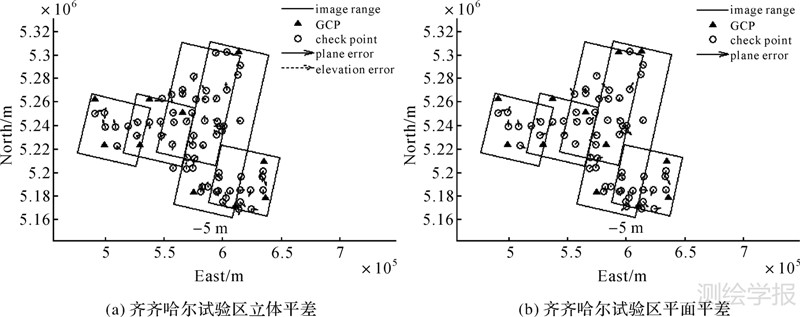
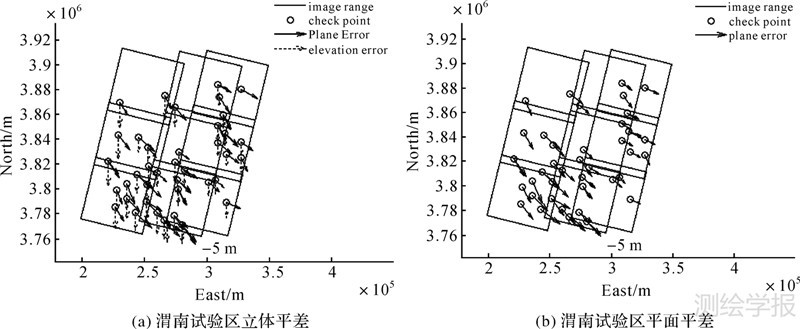
从表 2的结果可以看出,无论是平面平差或是立体平差,从自由网平差后检查点的残差来看均带有明显的系统性,即检查点残差的大小和方向在图中表现得较为一致,如图 2和图 4所示。在测区内分别布设了少量控制点后再进行带控制的区域网平差,此时通过控制点确定了平差的空间基准,并经最小二乘法则将误差进行了合理的配赋,再通过迭代计算使各点较好地收敛到一个最或是位置,从而明显提高了影像间的连接点和独立检查点的空间位置精度,如图 3和图 5。
|
| 图 2 齐齐哈尔测区自由网平差检查点的残差分布图 Fig. 2 Residual distribution of check points of free network adjustment in Qiqihar |
|
| 图 3 齐齐哈尔测区控制网平差检查点的残差分布图 Fig. 3 Residual distribution of check points of control network adjustment in Qiqihar |
|
| 图 4 渭南测区自由网平差检查点的残差分布图 Fig. 4 Residual distribution of check points of free network adjustment in Weinan |

|
| 图 5 渭南测区控制网平差检查点的残差分布图 Fig. 5 Residual distribution of check points of control network adjustment in Weinan |
其次,分别比较齐齐哈尔和陕西渭南两个试验区的结果不难发现,每个试验区在同一套控制和检查体系下,平面平差和立体平差所能达到的平面精度是一致的。这说明,在弱交会下的平面区域网平差中,DEM的作用相当于三线阵平差中的前后视影像所起到的高程约束作用。试验验证了平面区域网平差的平面精度能达到立体平差平面精度相当的水平。
3.4 不同精度DEM支持下平面平差试验对比表 2和表 3的结果中可以看出,在平面区域网平差中,连接点的高程控制无论是选择全球1000 m格网的DEM、90 m格网SRTM还是25 m格网的1∶50 000 DEM,均可以获得一致的平面精度。这是因为参与平面区域网平差的资源三号影像仅采用的是近似于垂直观测的正视全色影像,地形起伏引起的投影差非常小。对于资源三号正视全色影像,全球1000 m格网的DEM和90 m格网的SRTM可以起到同样高程约束的效果,并不会造成平面区域平差后检查点平面精度的下降。若对于侧摆角较大的卫星影像,平面区域网平差还是建议采用精度较高的DEM数据作为高程约束。
| 试验区 | DEM格网 | 平差方案 | 控制点/个 | 检查点/个 | 最大残差/m | 中误差/m | |||||
| E | N | 平面 | E | N | 平面 | ||||||
| 齐齐哈尔 | 90 | 无控平差 | 0 | 73 | 20.886 | 8.948 | 21.997 | 9.964 | 3.627 | 10.604 | |
| 带控平差 | 12 | 61 | 6.992 | 8.781 | 9.134 | 2.626 | 3.111 | 4.071 | |||
| 1000 | 无控平差 | 0 | 73 | 21.344 | 8.949 | 22.462 | 9.822 | 3.623 | 10.469 | ||
| 带控平差 | 12 | 61 | 6.794 | 8.781 | 9.135 | 2.624 | 3.106 | 4.066 | |||
| 陕西渭南 | 90 | 无控平差 | 0 | 52 | 15.710 | 18.368 | 20.315 | 9.611 | 9.450 | 13.478 | |
| 带控平差 | 9 | 43 | 5.953 | 7.227 | 7.439 | 2.485 | 3.010 | 3.903 | |||
| 1000 | 无控平差 | 0 | 52 | 18.666 | 18.854 | 22.694 | 10.350 | 9.623 | 14.133 | ||
| 带控平差 | 9 | 43 | 6.098 | 7.287 | 7.635 | 2.568 | 3.019 | 3.964 | |||
此外,由于平面平差中采用的DEM高程值均是不包含人工建筑的高度值的,因此在进行平面平差时控制点以及影像间的连接点一般不要选择在人工建筑上或者其附近。这是因为平面平差时地面点高程的初始值非常重要,若所赋地面点高程的初始值较差,该点通过迭代计算后可能无法收敛,导致平差发散。同理,地形陡峭以及地形变化剧烈的位置不能选择控制点和检查点。
4 结 论采用本文提出的弱交会条件下卫星影像平面区域网平差的方法,分别对两个不同地形区域的资源三号卫星正视全色影像进行了试验,并将其结果与资源三号卫星前正后三线阵立体平差的结果进行了比较。试验结果证实:
(1) 针对弱交会条件下卫星影像立体平差无法正确求解的问题,采用本文提出的平面平差方法是必要的,而且也是可行的。
(2) 在同一个区域采用相同的控制和检查体系的前提下,无论是自由网还是控制网,平面平差能够达到与立体平差相当的物方平面精度。
(3) 对于资源三号正视影像进行平面平差,利用1000 m格网、90 m格网和25 m格网的DEM作为平差过程中的高程约束,均可以保证平面区域网平差达到一致的精度。
| [1] | TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of ZY-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198. (唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191-198.) |
| [2] | LI Deren. Chinas First Civilian Three-line-array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica. 2012. 41(3):317-322. (李德仁. 我国第一颗民用三线阵立体测图卫星: 资源三号卫星[J]. 测绘学报, 2012, 41(3): 317-322.) |
| [3] | POLI D. General Model for Airborne and Spaceborne Linear Array Sensors[J]. International Archives of Photogrammetry and Remote Sensing, 2002, 34(B1): 177-182. |
| [4] | TOUTIN T. Spatiotriangulation with Multisensor VIR/SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2096-2103. |
| [5] | SHAO Juliang, WANG Shugen, LI Deren. Determination of Satellite Sensor Orientation[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(4): 329-333. (邵巨良, 王树根, 李德仁. 线阵列卫星传感器定向方法的研究[J]. 武汉测绘科技大学学报, 2000, 25(4): 329-333.) |
| [6] | WANG Renxiang. EFP Aerial Triangulation of Satellite Borne Three-line Array CCD Image (II) [J]. Science of Surveying and Mapping, 2002, 27(1): 1-7. (王任享. 卫星摄影三线阵CCD影像的EFP法空中三角测量(二)[J]. 测绘科学, 2002, 27(1): 1-7.) |
| [7] | CHENG Chunquan, DENG Kazhong, SUN Yushan, et al. Study of Block Adjustment for Long-strip Satellite CCD Images[J]. Acta Geodaetica et Cartographica Sinica. 2010, 39(2): 162-168. (程春泉, 邓喀中, 孙玉山, 等. 长条带卫星线阵影像区域网平差研究[J]. 测绘学报, 2010, 39(2): 162-168.) |
| [8] | TAO C V, HU Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347-1357. |
| [9] | FRASER C S, HANLEY H B, YAMAKAWA T. Three-dimensional Geopositioning Accuracy of IKONOS Imagery[J]. Photogrammetric Record, 2002, 17(99): 465-479. |
| [10] | GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59-68. |
| [11] | LI Deren, ZHANG Guo, JIANG Wanshou, et al. SPOT-5 HRS Satellite Imagery Block Adjustment without GCPs or with Single GCP[J]. Geomatics and Information Science of Wuhan University, 2006, 31(5): 377-380. (李德仁, 张过, 江万寿, 等. 缺少控制点的SPOT-5 HRS影像RPC模型区域网平差[J]. 武汉大学学报: 信息科学版, 2006, 31(5): 377-380.) |
| [12] | ZHANG Li, ZHANG Jixian, CHEN Xiangyang, et al. Block-adjustment with SPOT-5 Imagery and Sparse GCPs Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302-310. (张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302-310.) |
| [13] | WANG Taoyang, YUAN Xiuxiao. Block Adjustment for High-resolution Satellite Images[C]//Proceedings of the First Symposium on High Resolution Remote Sensing Data Processing and Applications. Xi’an: [s.n.], 2011, 63-69. (汪韬阳, 袁修孝. 高分辨率卫星遥感影像的区域网平差[C]//第一届全国高分辨率遥感数据处理与应用研讨会论文集, 西安: [s.n.], 2011, 63-69.) |
| [14] | ZHANG Guo. Rectification for High Resolution Remote Sensing Image under Lack of Ground Control Points[D]. Wuhan: Wuhan University, 2005. (张过. 缺少控制点的高分辨率卫星遥感影像几何纠正[D]. 武汉: 武汉大学, 2005.) |
| [15] | TEO T A, CHEN L C, LIU C L, et al. DEM-aided Block Adjustment for Satellite Images with Weak Convergence Geometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 8(4): 1907-1918. |
| [16] | LIU Jun, ZHANG Yongsheng, WANG Donghong. Precise Positioning of High Spatial Resolution Satellite Images Based on RPC Models[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 30-34. (刘军, 张永生, 王冬红. 基于RPC模型的高分辨率卫星影像精确定位[J]. 测绘学报, 2006, 35(1): 30-34.) |
| [17] | FRASER C S, HANLEY H B. Bias-compensated RPCs for Sensor Orientation of High-resolution Satellite Imagery[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(8): 900-9157. |
| [18] | TAO C V, HU Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347-1357. |
| [19] | JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. Research on the High Accuracy Band-to-band Registration Method of ZY-3 Multispectral Image [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 884-890. (蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星多光谱影像高精度谱段配准[J]. 测绘学报, 2013, 42(6): 884-890.) |
| [20] | PAN Hongbo, ZHANG Guo, TANG Xinming, et al. Accuracy Analysis and Verification of ZY-3 Products[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 738-744. (潘红播, 张过, 唐新明, 等. 资源三号测绘卫星影像产品精度分析与验证[J]. 测绘学报, 2013, 42(5): 738-744.) |