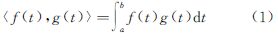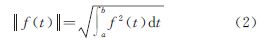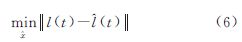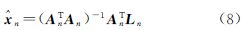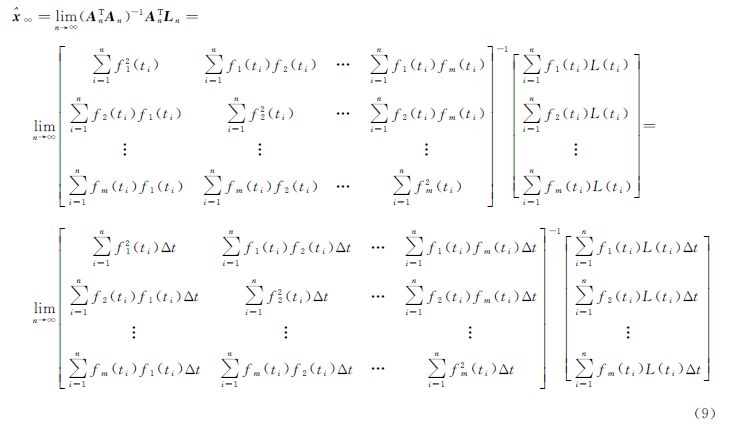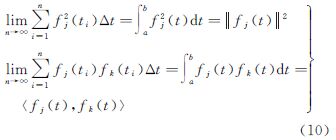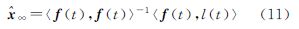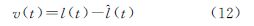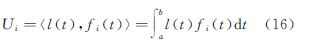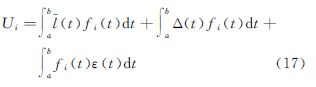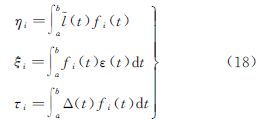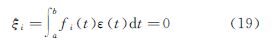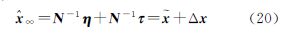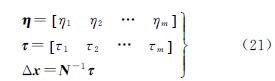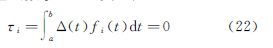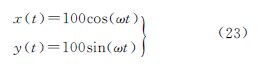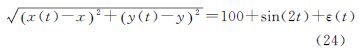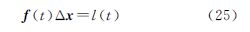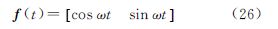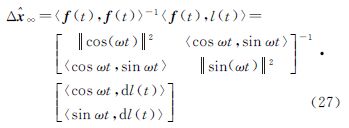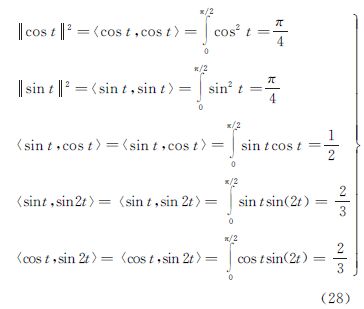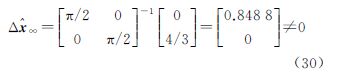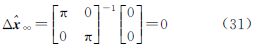2. 中国测绘科学研究院，北京 100830；
3. 西安测绘研究所 地理空间信息工程国家重点实验室，陕西 西安 710054
2. Chinese Academy of Surveying and Mapping,Beijing 100830,China;
3. National Key Laboratory of Geo-spatial Information,Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China
1 引 言
在误差理论中，一般将测量误差分为随机误差、系统误差和粗差，测量平差的研究对象多限于随机误差。包括有色噪声在内的各类系统误差处理是测量上的棘手问题之一，困难在于它既有系统性(某种规律性)，又有随机性[1]。若将有色噪声视为一种随机过程，则可通过其“延续性”对其进行数学处理，同时也可讨论有色噪声对平差的影响[1, 2]。文献[3]从导航定位观测量角度，论述了各种误差的区别、联系与转化，特别指出有色噪声是随时间变化而有规律变化的误差，观测时间越长有色噪声的影响一般越大。
连续观测是现代测量技术的重要特点之一，如GNSS卫星与地面连续观测站形成一个空间连续观测网络。利用时间序列分析和随机过程理论可以实现连续观测数据的噪声补偿和信息挖掘，如利用GNSS连续观测信息可提取对流层、电离层、地壳运动、地心运动等时变信号。在系统观测方案制定阶段，需要讨论有色噪声的抵偿方法，在测量数据平差阶段则需要考虑有色噪声的建模补偿方法[1, 2]。
连续观测系统的优化设计、观测结构分析与参数估计等离不开近代数学分析的支撑。在数学分析中，Hilbert空间是欧氏空间向无穷维空间的推广，其研究对象是函数空间[4]，是傅里叶分析和小波分析的理论框架。自20世纪50年代以来，利用Hilbert空间理论框架对测量平差问题进行了大量有益的探讨。这些研究通过将欧氏空间几何学理论和泛函分析思想引入测量平差，简化了有关公式的推导，揭示了测量平差问题的实质[5, 6, 7, 8, 9, 10]。基于Hilbert空间的傅里叶分析和小波分析在测量信号处理中也得到了非常广泛的应用[11, 12, 13]。
连续观测系统的平差一般在特定采样率下进行讨论，并将问题置于欧氏空间(有限维Hilbert空间)中研究。在动态测量系统平差方面，卡尔曼滤波也通常基于离散时间内分析其性能[2, 14]。表面上，可能会简化问题的复杂性，但是却可能掩盖连续观测系统平差的实质。不同的是，文献[15]提出了将积分多普勒定位的离散型误差方程组改化为分区间连续型的方法。
本文基于附加有色噪声的连续平差模型，从积分的定义和经典最小二乘解出发，探讨有限维测量平差问题向无穷维空间推广的方法。基于Hilbert空间理论，提出了连续平差模型；从经典最小二乘解出发，导出矛盾连续观测方程的最小二乘解，其解的严密性由连续平差模型的正交条件给出；讨论了连续平差模型参数无偏估计应满足的条件；以连续定位系统为例讨论了连续平差模型的求解方法和有色噪声的消除策略。
2 连续函数空间和连续平差模型 2.1 函数空间的基函数Hilbert空间是具有几何结构(度量或内积)的函数空间。在平方可积函数空间L2(a,b)={f(t)|∫abf2(t)dt＜∞}中，任意连续函数f(t),g(t)∈L2(a,b)的内积可定义为[4, 16]
由上述内积所定义的无穷维空间常代之以Hilbert空间。形象的，Hilbert空间是无穷维欧氏空间。令g(t)=f(t)，则由内积导出的范数为
在Hilbert空间中，若〈f(t),g(t)〉=0，称f(t)和g(t)是正交的。对于函数族f1(t)，f2(t)，…，f∞(t)∈L2(a,b)，若任意的i和j满足〈fi(t),fj(t)〉=0且||fi(t)||=||fj(t)||=1，则称该函数族为Hilbert空间的一组标准正交基。傅里叶分析的实质是函数在标准正交基下的一种正交投影。
2.2 连续观测系统的平差模型从信号处理角度，有色噪声泛指各种低频观测误差。在动态测量系统中，观测方程连续依赖于观测时间，一般存在大量有色噪声。若要揭示这些连续观测系统的平差实质，可将这些问题置于函数空间中进行讨论。从观测信息中提取这些低频信号所用的基函数选取较为灵活，既可选用正交基函数(如三角函数、小波函数等)，也可选取非正交基函数。而在测量平差中，基函数一般由观测方程的函数模型所唯一确定。本文将由基函数f(t)=[f1(t)f2(t) …fm(t)]和参数x=[x1x2…xm]T∈Rm所构成的方程
为连续观测方程。式中，l(t)∈L2(a,b)为连续观测值；l(t)∈L2(a,b)为连续观测真值；ε(t)∈L2(a,b)为连续观测高斯白噪声；Δ(t)∈L2(a,b)为有色噪声。若将有色噪声归为随机模型，则需要构建基于有色噪声的观测方差协方差模型，并需要讨论如何实现平差解的无偏性，若将其归为函数模型，则需要使用有色噪声经验函数模型进行改正，或者对有色噪声信号进行参数估计。若无有色噪声先验函数，可使用低频三角函数、小波函数等对其进行模拟[17]。 3 矛盾连续观测方程的最小二乘解
对于有限维Hilbert空间(欧氏空间)中的最小二乘问题Ax=l，因观测误差存在导致观测向量l∉R(A)={y|y=Ax,x∈Rm}[6, 7, 8]，其中，R(A)为系数矩阵A的列向量所确定的值域空间(子空间、子流形)[6, 18, 19]。类似于有限维平差，若克莱姆行列式det(N(t))≠0 [16, 20]，其中
且 det〈[f(t)l(t)],[f(t)l(t)]〉≠0(5) 则连续观测方程(3)为矛盾方程组，可使用最小二乘准则 确定观测信号的最佳逼近元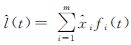
。
联系积分的定义和经典最小二乘平差理论，不难导出连续观测方程(3)在准则(6)下的最小二乘解。对连续观测方程(3)施加等时采样，可得离散观测方程
若将上式简记为Anxn=Ln，则观测方程(7)的最小二乘解为
数学家Hilbert研究积分方程时，曾将无穷维空间中的积分方程视为无穷多个线性方程组进行研究[4]。类似的，考虑式(8)给出的最小二乘解的极限，则
式中，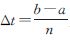
为采样间隔。由积分的定义可得
将式(10)代入式(9)，可得
可见，矛盾连续观测方程的最小二乘解可由经典最小二乘解的极限导出，且其形式与有限维空间中的经典最小二乘解十分类似。然而，连续平差模型(3)及其最小二乘解建立在信号分析的基础上，这为讨论连续观测中各类信号的提取和有色噪声的消除提供了方便。现代数学分析常将这类问题的解称为Hilbert空间中的最佳逼近元，并由正交投影定理导出[4]。
相应的，残差函数为
式中，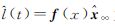
为观测信号的最小二乘逼近。||v(t)||反映了观测信号与基函数族f(t)所确定的值域空间的距离。
证明最小二乘解式(11)满足准则式(6)，仅需验证正交条件〈f(t),v(t)〉=0。
正交条件(13)与准则(6)的等价性由正交投影定理也不难得知[4]。
特别的，若f(t)为一组标准正交基，则最小二乘解(11)退化为
式(14)即为观测函数l(t)的傅里叶分析。可见，连续平差模型(3)及最小二乘解(11)是傅里叶分析的一种推广，即空间基函数f(t)从正交基向非正交基的一种推广。
4 有色噪声对平差解的影响分析下面讨论白噪声和有色噪声对平差解的影响。方便起见，记N=〈f(t),f(t)〉、U=〈f(t),l(t)〉，则
式中 为向量U的第i个分量。将l(t)=l(t)+Δ(t)+ε(t)代入式(16)，可得 设 式中，ηi为Ui的真值；τi为有色噪声Δ(t)在对Ui的影响。随机噪声ε(t)为高频信号，与信号fi(t)不相关，即 由此可得 式中 为参数估值的系统性偏差。当且仅当有色噪声信号Δ(t)与基函数fi(t)正交，即 时，参数估计才是无偏的，即Δx=0。
可见，当存在有色噪声时，连续平差模型的最小二乘解一般是有偏的。式(22)给出最小二乘解的无偏估计条件，即有色噪声函数正交于基函数。高频白噪声一般认为正交于基函数，故通过连续观测可以削弱。连续观测应尽量覆盖所有有色噪声的最大周期。对于低频有色噪声，则需长时间观测或模型改正。该结论也同样适用于观测误差(残差)的傅里叶分析。
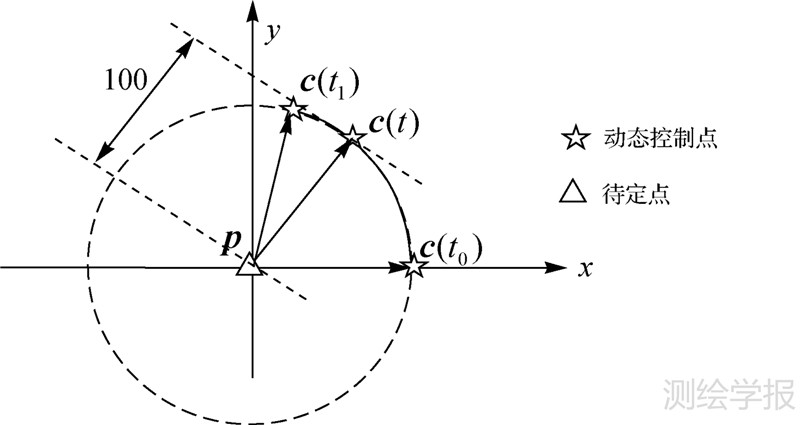
5 算例分析如图 1所示，构造一个二维连续测距定位系统：控制点围绕坐标原点p以角速度ω=1作匀速圆周运动(圆周半径为100)，控制点在t0=0时刻通过x轴，在t1时刻停止观测。控制点坐标可参数化为
使用正弦函数sin(2t)模拟有色噪声，则可将距离观测方程表示为
式中，[xy]为待定点p的坐标；ε(t)为高斯白噪声。在未知点初值[x0=0y0=0]处对距离观测方程(24)线性化可得 式中， 为观测方向余弦。则由式(11)可得矛盾方程组(26)的最小二乘解为
下面分别在3个观测时段t∈[0,π/2],t∈[0,π],t∈[0,2π]，采用连续平差模型和离散平差模型分析不同观测时长条件下有色噪声对坐标参数解的影响。
5.1 方案1：连续平差模型假设∫abcos(t)ε(t)dt=0、∫absin(t)ε(t)dt=0
(1) 当t∈[0,π/2]时，将关系式
代入式(27)，可得 此时，有色噪声引起的系统偏差在两个坐标分量方向均十分明显。
(2) 当t∈[0,π]时，可得
此时，有色噪声引起的系统偏差仅对第一个坐标方向明显。
(3) 当t∈[0,2π]时，可得
此时，参数估计无系统偏差。
事实上，只要观测时长不等于2π的整数倍，理论上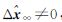
，即有色噪声不可能得到补偿，参数估计不满足无偏估计条件。由此不难理解，GNSS高精度定位观测方案观测时间长一般采用GNSS卫星运动的整数周期是十分合理的，否则应考虑使用更多的有色噪声改正模型。
设式(24)中的观测白噪声服从均值为零、方差为0.01的正态分布，即ε(t)～N(0,0.01)，分别在观测区间[0,π/2]、[0,π]和[0,2π]上的0.1s均匀采样观测进行最小二乘参数估计，并考察有色噪声对参数估计的影响。计算结果表明，方案1和方案2的最小二乘估值十分接近，当在区间[0,π/2]和[0,π]进行均匀采样时，离散最小二乘解为有偏估计量，仅当在观测区间[0,2π]进行均匀采样时，离散最小二乘解为无偏估计量。
若进一步将采样间隔提高为0.01s，则方案1和方案2的结果将趋于一致。这验证了式(9)、式(10)和式(11)的合理性，即连续平差模型的最小二乘解是经典离散最小二乘解的极限情形。在实践中，若基于动态控制点的参数方程(如GNSS卫星轨道)，将用户采样观测改化为连续观测信号(如傅里叶分析法)，则可有望利用本文提出的连续平差模型进行平差。
6 结 论(1) 本文提出的连续平差模型是经典测量平差模型向无穷维空间的一种推广。连续平差模型的最小二乘解是经典离散最小二乘解的极限。经典测量平差的许多结论对于连续平差模型也是成立的。
(2) 当连续平差模型的基函数为一组标准正交基时，连续观测方程平差退化为观测信号的傅里叶分析。
(3) 通过合理的观测系统设计和采样设计，可消除有色噪声，从而实现平差解的无偏估计。有色噪声函数正交于连续平差模型的基函数，是消除有色噪声的前提条件。
(4) 提高系统的采样频率只能消除观测高频噪声，有色噪声的消除取决于连续观测系统的重复观测周期和观测时长。最佳观测时长应覆盖有色噪声的整数周期，而并非采样时间越长越好。
(5) 在测量中，许多观测模型为连续数学模型，对这些模型进行采样不但增加计算成本，而且会损失精度。若使用傅里叶分析将离散实测数据消噪后建立连续观测函数，并建立连续观测平差模型，则有望简化计算。
| [1] | ZHOU Jiangwen. Mathematical Processing of Problems with Systematic Errors[J]. Engineering of Surveying and Mapping, 1999, 8(2): 1-4. (周江文. 系统误差的数学处理[J]. 测绘工程, 1999, 8(2): 1-4.) |
| [2] | YANG Yuanxi, CUI Xianqiang. Influence Functions of Colored Noises on Kinematic Positioning: Taking the AR Model of First Class as an Example[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 6-10. (杨元喜, 崔先强. 动态定位有色噪声影响函数: 以一阶AR模型为例[J]. 测绘学报, 2003, 32(1): 6-10.) |
| [3] | YANG Yuanxi. Some Notes on Uncertainty: Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650. (杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650.) |
| [4] | HUANG Zhenyou, YANG Jianxin, HUA Tahong, et al. Functional Analysis[M]. Beijing: Science Press, 2003.(黄振友, 杨建新, 华踏红, 等. 泛函分析[M]. 北京: 科学出版社, 2003.) |
| [5] | ZENG Linghou. Applications of Functional Analysis Method in Adjustment: Basic Theory[J]. Acta Geodaetica et Cartographica Sinica, 1962, 5(3): 176-183. (曾令候. 泛函方法在测量平差中的应用: 基本理论[J]. 测绘学报, 1962, 5(3): 176-183.) |
| [6] | YANG Yuanxi. Funcutional Analysis and Its Applications to Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 1986, 15(2): 110-114. (杨元喜. 泛函分析在最小二乘平差中的应用[J]. 测绘学报, 1986, 15(2): 110-114.) |
| [7] | DANG Songshi. Some Problems on the Adjustment in Surveying[J]. Acta Geodaetica et Cartographica Sinica, 1983, 12(3): 208-213. (党诵诗. 关于测量平差中的几个问题[J]. 测绘学报, 1983, 12(3): 208-13.) |
| [8] | ZHU Yonggang, BAI Yitong. Study of the Mathematical Structure of Adjustment Computation Based upon the Theory of Functional Analysis[J]. Geomatics and Information Science of Wuhan University, 1985, 29(4): 50-56. (祝永刚, 白亿同. 按泛函分析理论来剖析平差计算中的数学结构[J]. 武汉大学学报:信息科学版, 1985, 29(4): 50-56.) |
| [9] | TEUNISSEN P J G. Adjustment Theory: An Introduction[M]. 1st ed. Delft: Delft University Press, 2000: 168-173. |
| [10] | GRAFAREND E W. Linear and Nonlinear Models: Fixed Effects, Random Effects, and Mixed Models[M]. Berlin: Walter de Gruyter, 2006: 86-97. |
| [11] | WANG Ke, XIAO Pengfeng, FENG Xuezhi, et al. The Modified Algorithm of Image Edege Features Detection from Phase Congruency Model Based on 2-D Hilbert Transformt[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. (王珂, 肖鹏峰, 冯学智, 等. 基于改进二维离散希尔伯特变换的图像边缘检测方法[J]. 测绘学报, 2012, 41(3): 421-427.) |
| [12] | TAN Kun, DU Peijun. Wavelet Support Vector Machines Based on Reproducing Kernel Hilbert Space for Hyperspectral Remote Sensing Image Classification[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 142-147. (谭琨, 杜培军. 基于再生核Hilbert空间小波核函数支持向量机的高光谱遥感影像分类[J]. 测绘学报, 2011, 40(2): 142-147.) |
| [13] | LI Xinwu, GUO Huadong, LIAO Jingjuan, et al. Baseline Estimation of Interferometric SAR Based on Fast Fourier Transform[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 70-72. (李新武, 郭华东, 廖静娟, 等. 基于快速傅里叶变换的干涉SAR基线估计[J]. 测绘学报, 2003, 32(1): 70-72.) |
| [14] | LIU Dajie, YU Zhenglin. Dynamic Surveying System and Kalman Filter[J]. Acta Geodaetica et Cartographica Sinica, 1988, 17(4): 254-262. (刘大杰, 于正林. 动态测量系统与卡尔曼滤波[J]. 测绘学报, 1988, 17(4): 254-262.) |
| [15] | WANG Jiazhen. A Solution of Doppler Single Point Positioning by Fitting Free Terns[J]. Acta Geodaetica et Cartographica Sinica, 1988, 17(1): 9-20. (汪嘉祯. 拟合自由项解算多普勒单点定位[J]. 测绘学报, 1988, 17(1): 9-20.) |
| [16] | COURANT R, HILBERT D. Methods of Mathematical Physics[M]. New York: John Wiley & Sons, 1989. |
| [17] | CHEN Yongqi, WU Zian, WU Zhongru. Deformation Monitoring Analysis and Forecasting[M]. Beijing: Surveying and Mapping Press, 1981: 136-148. (陈永奇, 吴子安, 吴中如. 变形监测分析与预报[M]. 北京: 测绘出版社, 1998: 136-148.) |
| [18] | XUE Shuqiang, DANG Yamin, CHEN Wu. Matrix Volume Method of the Mean Square Deviation Computation of Least Square Solution[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1106-1119. (薛树强, 党亚民, 陈武. 最小二乘估值均方差计算的矩阵体积法[J]. 武汉大学学报: 信息科学版, 2009, 34(9): 1106-1119.) |
| [19] | XUE Shuqiang. Matrix Volume and Its Applications in Network Design[D]. Beijing: Chinese Academy of Surveying and Mapping, 2007. (薛树强. 矩阵体积及其在网形设计中的应用[D]. 北京: 中国测绘科学研究院, 2007.) |
| [20] | SERRE D. Matrices: Theory and Applications[M]. 2nd ed. New York: Springer, 2010. |
| [21] | XUE S Q,YANG Y X, DANG Y M, et al. Dynamic Positioning Configuration and Its First-order Optimization[J]. Journal of Geodesy, 2014, 88(2): 127-143. |