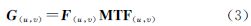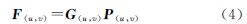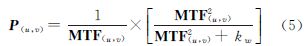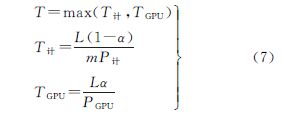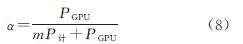1 引 言
高分辨率卫星影像在成像过程中受大气扰动、平台震颤、传感器性能下降等因素影响,致使影像质量退化。基于调制传递函数(modulation transfer function,MTF)理论的图像复原方法是目前较为常用的改善高分辨率卫星影像质量的方法。该方法通过计算成像系统的MTF曲线在不同空间频段的下降程度来反推实际影像频谱中高频部分的上升程度,达到改善影像质量的目的[1]。由于需要对影像进行较为复杂的逐像素频域滤波处理,因此MTF补偿的计算量很大。特别是在卫星数据源快速增多、空间分辨率大幅提高、需要处理的影像数据量急剧增长的背景下,传统的MTF补偿计算时间长、效率低下等问题日益明显,已无法满足在许多应急应用领域(如军事情报判读、抢险救灾)中对卫星影像进行实时或准实时MTF补偿处理的要求,成为制约整个高分辨率卫星数据处理快速完成的瓶颈。
近年来,随着半导体技术和计算机技术的发展,图形处理单元(graphics processing unit,GPU)的计算性能以超过摩尔定律的速度不断提高,已成为当前计算机系统中具备高性能处理能力的部件。目前,国内外相关学者对使用GPU提高计算密集型遥感数据处理算法的效率开展了一些研究:文献[2]使用GPU进行高光谱影像非监督波段选取试验,算法效率提高22倍;文献[3]使用GPU对光学航空影像进行几何校正,算法加速比达到45倍;文献[4]在GPU上建立红外大气探测干涉仪的辐射传输模型,获得了上百倍的加速比。在国内,文献[5]实现了基于GPU的并行影像匹配算法,将影像匹配速度提高了7倍。从上述应用可以看出,虽然各算法加速比不一致(与硬件环境、算法特点有关),但处理效率都明显提高。MTF补偿计算密集,且逐像元进行,具有先天并行性,非常适合于在GPU上进行处理。文献[6]使用CPU/GPU对资源三号卫星影像进行MTF补偿,取得了较好的效果,但其性能优化并不充分,算法效率仍有进一步提高空间。本文使用基于Fermi架构的新一代GPU,综合考虑充分利用CPU的计算性能,系统地探讨使用CPU/GPU协同处理理论对高分辨率卫星影像进行MTF补偿的方法,涉及方法在GPU上的实现、性能的充分优化以及CPU和GPU间负载分配等一系列问题。
2 原理与方法 2.1 MTF补偿原理设f(x,y)为原始未退化影像,g(x,y)为观测到的退化影像,退化的数学模型为[7]
式中,h(x,y)为点扩散函数;*代表卷积操作。对两边进行傅里叶变换,得频域表达形式
式中,H(u,v)的值是复数,若对幅值作归一化,使得零频率的幅值为1,则称此归一化的幅值为调制传递函数(MTF)[1]。因此,退化模型可变为计算上式中MTF的理论和方法有许多,主要包括点脉冲法、正弦输入法、刀刃法和脉冲法[8, 9, 10],其中后两种方法运用情况更为普遍。这两种方法需要从卫星在轨运行获取的影像中抠取靶标子图,通过子图中的边缘地物或线性地物生成MTF曲线,并构造二维MTF矩阵。由于靶标子图较小,计算量不大,因此所需时间较短。关于MTF曲线生成和二维MTF矩阵构造可参见文献[10, 11]。
MTF补偿是退化模型的逆过程,在实际应用中对退化影像进行MTF补偿时,需要选取一个包含MTF矩阵的滤波算子P,其表达形式为
常用的滤波算子包括逆滤波、维纳滤波、修正反转滤波、约束最小二乘方滤波和Lucy-Richardson滤波等。其中维纳滤波考虑了噪声的影响,是一种很常用的图像恢复算子,可直接应用于频率域[7, 11, 12]。频率域的维纳滤波算子如下式所示
式中,MTF(u,v)是二维MTF矩阵;kw是与图像信噪比有关的先验常数。 2.2 CPU/GPU协同处理在当前主流的CPU/GPU协同处理系统中,通常包含一个多核CPU和一片众核GPU。其中在多核CPU上应用最广泛的编程模型是OpenMP。OpenMP是共享存储系统并行编程的工业标准,提供对并行区域、工作区间共享、同步等处理的支持。OpenMP可直接在高级语言(如C、Fortran)的串行代码上实现并行:在源代码中嵌入编译制导语句,编译后执行时制导语句启动多线程环境实现并行计算,不需要对程序做大的修改[13]。关于OpenMP的详细内容可参见文献[13]。
早期的GPU开发直接使用图形学API(如OpenGL、DirectX等)进行编程,程序员需要对图形学硬件和编程接口有深入的了解,开发难度较大,因此应用并不广泛。2007年,NVIDIA公司推出了统一计算设备架构(compute unified device architecture,CUDA),该架构通过简单易用的类C语言进行开发,能够比较容易地获得几倍、几十倍,乃至上百倍的加速效率,得到了非常广泛的使用[14]。CUDA 实际上是一种“串行—并行”混合的CPU/GPU协同编程模型:需要并行处理的部分被组织成“核函数”,“核函数”启动时产生大量线程,这些线程以线程网格和线程块的形式进行层次性组织,同时对数据进行并行化处理;其余串行执行步骤由CPU进行处理,这些步骤主要包括在CPU和GPU间传输数据、配置核函数执行参数、启动核函数并行执行程序等[15, 16, 17]。此外,CUDA设计了一个层次性存储体系,包括全局存储器、常数存储器、共享存储器等,这些存储器的存储容量和访问速度互不相同。关于CUDA编程模型、线程组织结构和层次性存储体系等详细内容可参见文献[15, 18]。
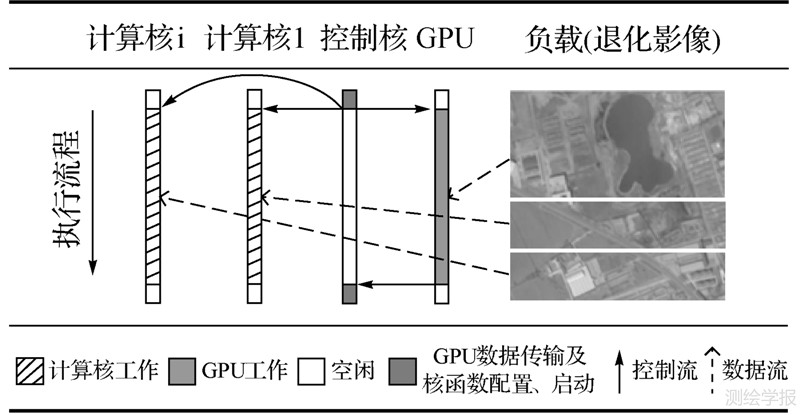
2.3 负载分配的CPU/GPU MTF补偿方法在CPU/GPU协同处理系统中进行MTF补偿时,需要单独指派一个CPU核与GPU进行交互(CPU和GPU之间的数据传输、核函数执行参数配置、核函数启动等),本文将其命名为“控制核”;此外,为充分利用系统中其余CPU核的计算性能,将其作为“计算核”,与GPU一起共同完成对负载(即退化影像)的MTF补偿处理,如图 1所示。其中GPU方法实现及性能优化、控制核和GPU之间的交互使用CUDA实现;计算核并行区域构造、控制核与计算核之间的交互使用OpenMP实现。GPU和计算核之间的负载分配依据负载分配策略进行,该策略根据计算核的数量和方法的实际加速比为计算核和GPU合理分配对应的负载量,使得方法的总执行效率达到最优。
|
| 图 1 负载分配的CPU/GPU MTF补偿方法 Fig. 1 The workload-distribution based CPU/GPU MTF compensation approach |
由于需要进行逐像素频域滤波,计算较为复杂,因此GPU上的MTF补偿被划分为3个核函数实现:ConvertToComplex、Compensation和ConvertFromComplex。其中ConvertToComplex将影像数据类型转为在GPU上进行傅里叶变换所需的Complex数据类型,Compensation执行频域维纳滤波,ConvertFromComplex将Complex数据类型转回为影像数据类型。傅里叶变换使用NVIDIA提供的CUDA快速傅里叶变换(CUDA fast Fourier transform,CUFFT)函数库实现。在核函数中,将线程块中线程数量设置为Fermi架构GPU的上限1024(32×32),且每个线程负责对一个像素进行处理。因此,若设退化影像的大小为lwidth×lheight,则共需产生[lwidth/32]×[lheight/ 32]个线程块完成对整幅影像的处理(进行向上取整的原因是保证所有像素皆被覆盖)。
上述方法仅为基本实现,可保证MTF补偿在GPU上顺利完成,但无法充分发挥GPU的计算能力。因此需对方法进行性能优化,主要通过以下3个方面展开:
(1) 执行配置优化可进一步细分为提高流式多处理器中线程占有率和线程多元素重访两个策略。在提高流式多处理器中线程占有率方面,基于Fermi架构的GPU需要在满足如下两个限制条件的前提下,使流式多处理器中线程占有率达到最高(流式多处理器中包含1536个线程)[18],以提高GPU线程调度的性能:①线程块中线程数量小于1024;②流式多处理器中线程块数量小于8。
经过分析,当线程块中线程数量设置为256或512时,流式多处理器中线程块数量分别为6或3,同时满足限制条件。在这两种情况下,流式多处理器都包含1536个线程,线程占有率达到最高。
线程多元素重访策略利用GPU上多次显存访问可被流水化以及线程寻址可重用等特点,令一个GPU线程同时处理多个像素,以提高GPU上线程运行的性能。需要注意的是,GPU线程运行的性能并不会随着线程访问像素量的增加而无限增长,而是存在一个峰值,因此需根据实际情况找出性能达到峰值时GPU线程对应处理的像素量,使算法执行效率达到最优。
(2) 存储访问优化也可细分为两个策略:存储层次性访问和传输计算堆叠。在存储层次性访问方面,基于Fermi架构的GPU除全局存储器外,还提供了由共享存储器和一级缓存共同组成的容量为64KB的片上缓存。该片上缓存可柔性重组,提供两种容量分配模式:①48KB共享存储器+16KB一级缓存;②16KB共享存储器+48KB一级缓存[19]。在核函数Compensation进行维纳滤波的过程中,MTF矩阵被多次使用,因此可将其载入至共享存储器中,减少程序访问全局存储器的次数;又为了一次性尽可能多地载入MTF矩阵,故选择分配模式①,并通过式(6)确定每个线程对应处理的像素量,使得共享存储器空间被完全利用。ConvertToComplex和ConvertFromComplex两个核函数无数据重复性访问,因此选择分配模式②,将更多影像缓存至一级cache;由于没有使用共享存储器,因此这两个核函数的每个线程仍然对应处理一个像素。
在CUDA中,数据在内存和GPU显存之间的传输默认为串行阻塞式传输,即数据完全从内存拷贝至GPU显存后,GPU核函数才能执行;当GPU核函数执行完毕后,数据再从GPU显存中拷回至内存。基于Fermi架构的GPU内部固化有一个数据拷贝引擎和一个核函数执行引擎,因此可使用流机制来实现数据传输和计算的堆叠。流是一个“先进先出”的命令流水线[18],包含1次内存至显存数据拷贝操作、5次核函数执行操作(ConvertToComplex、傅里叶正变换、Compensation、傅里叶逆变换和ConvertFromComplex)和1次显存至内存数据拷贝操作。当程序开始执行时,GPU底层硬件将数据拷贝操作映射至数据拷贝引擎,将核函数执行操作映射至核函数执行引擎,随后这两个引擎异步执行相应的任务,实现数据传输和计算的堆叠。
(3) 指令优化。为达到更高的处理效率,GPU上放置了数百个计算核心,远多于CPU上计算核心的数量。因此与CPU相比,GPU上控制部件较少,使得GPU对控制逻辑的处理能力较弱:一些高级语言中常用的控制逻辑(如线程束内部“if-else”分支、“for”循环等)在GPU上的执行时间远长于在CPU上的执行时间,导致GPU性能损失。在3个核函数中,由于横纵坐标方向的线程数大于影像像素个数,因此在边界像素处理时引入了逻辑分支,但这些分支语句为逐像素分支,不属于线程束内部的逻辑分支,故不会导致性能损失;在核函数Compensation中,为充分利用共享存储器,每个线程对应处理的像素量会多于1个,因此会产生“for”循环的使用,并使程序执行性能下降;为提高性能,需进行循环解缠处理(将循环逻辑展开为顺序逻辑执行)。ConvertToComplex和ConvertFromComplex两个核函数中每个线程仍对应一个像素的工作量,因此无需循环解缠。循环解缠前后核函数Compensation的执行流程如表 1所示(假设每个线程对应处理n个像素)。
| 算法1:循环解缠前Compensation执行流程 | 算法2:循环解缠后Compensation执行流程 |
| 01: For i=1 to n do | 01: 将第1部分MTF矩阵载入共享存储器 |
| 02: 将第i部分MTF矩阵载入共享存储器 | 02: …… |
| 03: Endfor | 03: 将第n部分MTF矩阵载入共享存储器 |
| 04: 线程同步 | 04: 线程同步 |
| 05: For i=1 to n do | 05: 对第1部分影像进行MTF补偿 |
| 06: 对第i部分影像进行MTF补偿 | 06: …… |
| 07: Endfor | 07: 对第n部分影像进行MTF补偿 |
| 08: 线程同步 | 08: 线程同步 |
综上所述,性能优化后的CPU/GPU MTF补偿流程如图 2所示,其中灰色标记的步骤表示使用流实现了传输计算堆叠。

|
| 图 2 性能优化后的CPU/GPU MTF补偿流程(灰色标记步骤表示使用流实现了传输计算堆叠) Fig. 2 The CPU/GPU MTF compensation approach after performance tuning (the gray-marked steps are streamed for the overlap of data transfer and computation) |
为充分利用系统中计算核的计算性能,将其与GPU一起共同完成对负载(即退化影像)的MTF补偿处理。在这种情况下,需为两者合理分配负载量,使方法的总执行效率达到最优。令P计、PGPU、m和α分别代表计算核的理论峰值计算性能(假设所有计算核的计算性能都相同)、GPU的理论峰值计算性能、计算核的数量以及分配给GPU的负载率。若总负载量为L,则方法总执行时间T由下式确定
容易发现,当计算核和GPU同时完成处理时(T计= TGPU),整个方法执行时间最短,即当α由下式决定时,T值最小
通常情况下,计算核和GPU的理论峰值计算性能都无法达到。因此,在实际应用中,可用MTF补偿的GPU版本相对CPU串行版本的加速比替代PGPU和P计。令s代表加速比,替换PGPU/P计,则由式(8)可得
3 试验结果与分析2013年4月26日,我国高分辨率对地观测卫星系统首星“高分一号”成功发射升空,该卫星搭载两台2m分辨率全色/8m分辨率多光谱相机和4台16m分辨率多光谱相机。其中全色相机采用10bit量化,标准景影像大小为18192像素×18499像素,数据量较大(约642MB),具有较好的代表性,因此本节选择该影像作为试验影像。
本节使用加速比来评价本文方法相对于传统串行方法执行效率的提升,定义如下
式中,TCPU为传统串行方法在CPU上的执行时间;TCPU/GPU为本文方法在CPU/GPU系统上的执行时间,由两部分组成:数据在内存和GPU显存之间的传输时间和GPU实际执行时间;s为加速比。此外,使用性能提升比来评价某一优化手段作用前后方法执行效率的提升,定义如下
式中,Tbef和Taft分别为某一优化手段作用前后方法的执行时间;p为性能提升比。 3.1 方法性能本文试验环境中的CPU为Intel Xeon E5650,含6个处理核心,单精度浮点峰值运算能力约为128Gflops;GPU选择当前主流的基于Fermi架构的NVIDIA Tesla C2050,含448个处理核心,单精度浮点峰值运算能力约为1030 Gflops。此外,NVIDIA Tesla C2050的片上缓存大小为64KB(可柔性重组),全局存储器容量为3GB,内部含有一个数据拷贝引擎和一个核函数执行引擎;主机内存大小为24GB;全局存储器和内存之间通过PCIE2.0×16接口进行通信;试验平台为Win32(在此平台上编译和执行的程序为32位)。由于影像数据量较大,超过了32位程序一次能分配的最大内存,本试验将影像划分为1024像素×1024像素大小的数据块进行分块载入和处理,保证内存的成功分配。试验影像标准景大小为18192像素×18499像素,若将左上边数据块与影像左上角对齐,则划分给最右边和最下边数据块的像素不足1024(分别为784和67),可采取将无像素部分填0的方法将数据块补齐至1024像素×1024像素,然后再与其余数据块相同的方式进行MTF补偿,补偿完毕后只保存对应像素即可。
首先测得在试验环境的CPU上MTF曲线生成、二维MTF矩阵构造以及MTF补偿的执行时间,如表 2所示。其中MTF曲线生成选用刀刃法,作用于从退化影像扣取的靶标子图上(30像素×30像素,1.8KB);二维MTF矩阵构造选择文献[11]中方法,矩阵大小与数据块大小保持一致(1024像素×1024像素,4MB);MTF补偿按分块策略进行,作用于高分一号全色标准景影像上(18192像素×18499像素,641MB)。补偿过程中的傅里叶正/反变换采用快速傅里叶变换(fast Fourier transform in the west,FFTW)函数库实现。
| s | |
| 算法类别 | CPU执行时间 |
| MTF曲线生成 | 0.15 |
| 二维MTF矩阵构造 | 0.05 |
| MTF补偿 | 77.47 |
从表中可知,与MTF曲线生成和二维MTF矩阵构造相比,MTF补偿执行时间最长,约占整个图像复原处理执行时间的99.7%,成为制约整个处理流程快速完成的瓶颈。故需使用本文方法对其进行加速处理,提高处理效率。
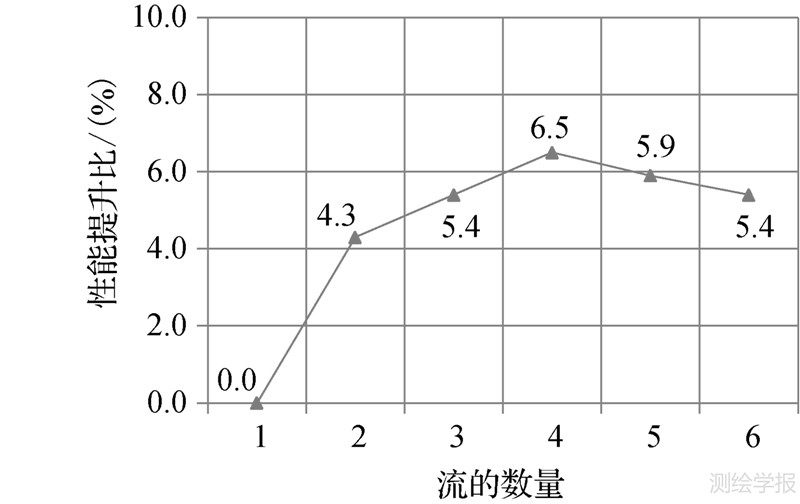
经测试,在试验环境的GPU上,仅进行基本实现(未进行性能优化)的MTF补偿方法的执行时间为3.39s,对应的加速比达到22.85倍。接下来使用3种性能优化策略对方法进行优化:首先进行执行配置优化,将线程块中线程数量设置为256,使流式多处理器中的线程占有率达到最高,并使用线程多元素重访策略令一个GPU线程处理多个像素,图 3列出了随着GPU线程处理像素数量变化,方法性能提升比的变化情况,从图中可以发现,当GPU线程对应处理4个像素时,方法的执行效率最优,对应的性能提升比为5.1%;其次使用存储层次性访问策略,对片上缓存进行动态分配并将MTF矩阵载入至共享存储器中,又为了充分利用共享存储器,根据式(6)计算核函数Compensation中每个线程对应处理的像素量:动态分配后共享存储器容量为48KB;流式多处理器中线程数量经优化后为1536;数据类型为4字节单精度浮点型(Complex数据类型中的实部[20]),因此可算出每个线程对应8个像素的工作量;接下来使用流实现传输计算堆叠,从图 4可知,当创建4个流的时候,方法的性能提升比最高(6.5%),由于流的创建和销毁会带来额外的开销,因此创建过多的流反而会导致方法性能下降;最后进行指令优化,对核函数Compensation进行循环解缠处理。

|
| 图 3 使用线程多元素重访策略后方法的性能提升比 Fig. 3 The performance improvement ratio after assigning each GPU thread the workload of multiple pixels |
|
| 图 4 使用流实现传输计算堆叠后方法的性能提升比 Fig. 4 The performance improvement ratio after creating multiple streams |
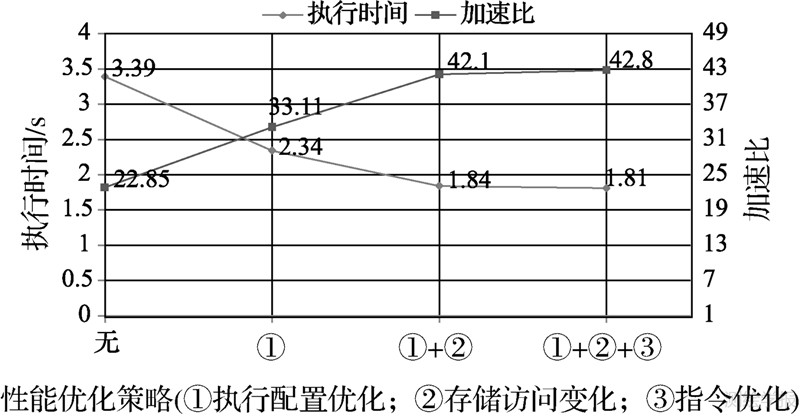
图 5列出了逐步使用3种性能优化策略后,在试验环境的GPU上MTF补偿的执行时间和加速比。可以看出,执行配置优化后,方法加速比从22.85倍提高到33.11倍,性能提升最为明显,达到44.9%;在此基础上进行存储访问优化后,方法性能进一步提升,加速比达到42.10倍;当对核函数Compensation进行循环解缠处理后,整个方法的处理时间压缩至1.81s,相应的加速比达到42.80倍。此外,还采用了文献[6]中的方法对试验影像进行了MTF补偿,由于未使用线程多元素重访和传输计算堆叠进行性能优化,整个方法的执行时间为2.02s,相应的加速比仅为38.35倍。故本文方法的执行效率较优。
|
| 图 5 逐步使用性能优化策略后GPU上MTF补偿的执行时间和加速比 Fig. 5 The run time and speedup ratio of MTF Compensation after gradually applying three optimization approaches on GPU |
接下来使用CPU/GPU负载分配策略将部分负载(退化影像)分配给CPU计算核进行处理,进一步提高方法的执行效率。试验环境中的CPU为6核Intel Xeon E5650,其中1个核用作控制核,其余5个核可作为计算核;此外,方法加速比已知。因此可通过式(9)计算出理论上分配给GPU和计算核的负载率。令式(9)中m为5,s为42.80,可得到α的理论值为0.895。即理论上,分配给GPU的负载百分比为89.5%;相应的,分配给计算核的负载百分比为10.5%。在具体实施时,使用OpenMP的parallel子句创建6个线程,然后通过相应的OpenMP API(omp_get_thread_num()函数)获取线程号并给其指派任务,其中1个线程作为控制核线程与GPU交互,其余5个线程作为计算核线程,共同对分配给计算核的负载进行并行处理(其中正反傅里叶变换的并行化通过调用FFTW函数库内嵌的多线程接口实现,影像数据类型和Complex数据类型的相互转换以及维纳滤波的并行化通过线程间任务分配进行)。
为验证理论值的正确性,本文实测了在GPU对应负载率变化的情况下GPU和CPU的执行时间,如图 6所示。从图中发现,当GPU对应负载率为0.893时,GPU和CPU的执行时间相等(1.62s),实际值与理论值之间存在一个大小为0.002细微误差。可将该误差归结于CUDA运行时环境初始化带来的时间开销,使得GPU执行时间不与其对应负载率严格成正比关系:当GPU对应负载率趋近于0时,GPU执行时间并不趋近于0(当GPU对应负载率仅为0.005时,GPU执行时间仍为0.31s),而是趋近于该额外的时间开销。因此,在实际应用中,可首先根据式(9)计算得到理论上的GPU负载分配率,然后再减去一个微小修正量,得到更为精确的分配率。

|
| 图 6 GPU对应负载率变化时GPU和CPU的执行时间变化情况 Fig. 6 The variation of GPU and CPU run time with different workload ratio for GPU |
对各版本MTF补偿方法执行时间和加速比进行统计,如表 3所示。在使用负载分配策略后,方法执行效率进一步提高,最终加速比达到47.82倍,相应的执行时间压缩至1.62s,可以满足对高分辨率卫星影像进行近实时MTF补偿的需求。
| 版本 | CPU执行 时间/s | GPU执行 时间/s | 加速比 |
| CPU串行 | 77.47 | — | — |
| GPU性能优化前 | — | 3.39 | 22.85 |
| GPU性能优化后 | — | 1.81 | 42.80 |
| GPU性能优化后 +负载分配 | 1.62 | 1.62 | 47.82 |
为验证本文方法的正确性,将经CPU处理得到的影像和由GPU处理得到的影像进行逐像素比对,发现两者完全相同,说明方法的正确性得到了保证。实际上,基于Fermi架构的GPU的浮点运算精度完全满足IEEE 754-2008浮点运算标准[20],因此对于需要进行浮点运算的程序,选择基于Fermi架构的GPU可完全保证计算结果的准确性和精度。
4 结 论本文系统地探讨了负载分配的CPU/GPU高分辨率卫星影像MTF补偿方法。首先阐述了方法的基本实现,然后通过3种GPU性能优化策略(执行配置优化、存储访问优化和指令优化)对方法性能进行优化。使用本文方法在NVIDIA Tesla C2050 GPU上对高分一号卫星全色影像进行MTF补偿,与传统CPU串行方法相比,加速比达到42.80倍,优于文献[6]中方法。此外,为充分利用CPU的计算性能,提出了负载分配策略,该策略根据系统中计算核的数量和方法的实际加速比为计算核和GPU分配对应的负载量,保证方法的总执行效率达到最优。使用该策略后,方法执行效率进一步提高,最终加速比达到47.82倍,相应处理时间压缩至1.62s,可以满足对高分辨率卫星影像进行近实时MTF补偿的处理需求。此外,由于Tesla C2050 GPU的浮点运算精度完全满足IEEE 754-2008浮点运算标准,使用本方法处理得到的影像与使用传统串行CPU方法处理得到的影像完全相同,说明了方法的正确性。
| [1] | CHEN Qiang,DAI Qiyan,XIA Deshen. Restoration of Remote Sensing Images Based on MTF Theory [J]. Journal of Image and Graphics,2006,11(9):1299-1305.(陈强,戴奇燕,夏德深. 基于MTF理论的遥感影像复原[J]. 中国图象图形学报,2006,11(9):1299-1305.) |
| [2] | YANG H,DU Q,CHEN G S. Unsupervised Hyperspectral Band Selection Using Graphics Processing Units [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2011,4(3):660-668. |
| [3] | JAVIER R S,MARIA C C,JULIO M H. Geocorrection for Airborne Pushbroom Imagers [J]. IEEE Transactions of Geoscience and Remote Sensing,2012,50(11):4409-4419. |
| [4] | MIELIKAINEN J,HUANG B,HUANG H L. GPU-accelerated Multi-profile Radiative Transfer Model for the Infrared Atmospheric Sounding Interferometer [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2011,4(3):691-699. |
| [5] | XIAO Han, ZHANG Zuxun. Parallel Image Matching Algorithm Based on GPGPU [J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):46-51.(肖汉,张祖勋. 基于GPGPU的并行影像匹配算法[J]. 测绘学报,2010,39(1):46-51.) |
| [6] | FANG L Y,WANG M,LI D R,et al. CPU/GPU Near Real-time Preprocessing for ZY-3 Satellite Images: Relative Radiometric Correction, MTF Compensation and Geocorrection [J]. ISPRS Journal of Photogrammetry and Remote Sensing,2014,87:229-240. |
| [7] | GE Ping,WANG Mi,PAN Jun,et al. A Study of Adaptive Image Restoration of High Resolution TDI-CCD Image Data [J]. Remote Sensing for Land and Resources,2010 (4):23-28.(葛苹,王密,潘俊,等. 高分辨率TDI-CCD成像数据的自适应MTF图像复原处理研究[J]. 国土资源遥感,2010 (4):23-28.) |
| [8] | ZHANG Ying,HE Binbin,LI Xiaowen. Remote Sensing Image Fusion of Beijing-1 DMC+4 Microsatellite Based on MTF Filter [J]. Acta Geodaetica et Cartographica Sinica,2009,38(3):223-228.(张瑛,何彬彬,李小文. 基于MTF滤波的北京一号小卫星遥感影像融合[J]. 测绘学报,2009,38(3):223-228.) |
| [9] | LEE D H,YANG J Y,SEO D C,et al. Image Restoration of the Asymmetric Point Spread Function of a High-resolution Remote Sensing Satellite with Time-delayed Integration [J].Advances in Space Research,2011,47:690-701. |
| [10] | CAI Xinmin. MTF Calculation and Analysis Based on Satellite Remote Sensing Images [D]. Nanjing:Nanjing University of Science and Technology,2007.(蔡新明. 基于卫星遥感图像的MTF计算和分析[D]. 南京:南京理工大学,2007.) |
| [11] | GU Xingfa,LI Xiaoying,MIN Xiangjun,et al. MTF On-orbit Measurement and Image Compensation for CBERS-02 CCD Imager [J]. Science in China Information Sciences,2005,35(1):26-40.(顾行发,李小英,闵祥军,等. CBERS-02卫星CCD相机MTF在轨测量及图像MTF补偿[J]. 中国科学E辑:信息科学,2005,35(1):26-40.) |
| [12] | LI Xiaoying,GU Xingfa,YU Tao,et al. Image-derived MTF Method and MTF Compensation for CBERS-02B WFI Imager [J]. Journal of Remote Sensing:2009,13(3):371-384.(李小英,顾行发,余涛,等. CBERS-02B卫星WFI成像在轨MTF估算与图像MTF补偿[J]. 遥感学报,2009,13(3):371-384.) |
| [13] | KUCK D J, CHAPMAN B, JOST G,et al. Using OpenMP: Portable Shared Memory Parallel Programming[M]. Massachusetts:MIT Press,2007. |
| [14] | YANG Jingyu. Study on Parallel Processing Technologies of Photogrammetry Data Based on GPU [D]. Zhengzhou:Information Engineering University,2011.(杨靖宇. 摄影测量数据GPU并行处理若干关键技术研究[D].郑州:信息工程大学,2011.) |
| [15] | ZHANG Shu,CHU Yanli. GPU High Performance Computing: CUDA [M]. Beijing:China Waterpower Press,2009.(张舒,褚艳利. GPU 高性能运算之CUDA [M]. 北京:中国水利水电出版社,2009.) |
| [16] | ZHAO Jin. Study of Remote Sensing Image Parallel Processing Algorithms based on GPU and Optimization Techniques [D]. Changsha:The National University of Defense Technology, 2011.(赵进. 基于GPU的遥感图像并行处理算法及其优化技术研究[D]. 长沙:国防科学技术大学,2011.) |
| [17] | LU Fengshun,SONG Junqiang,YIN Fukang et al. Survey of CPU/GPU Synergetic Parallel Computing [J]. Computer Science,2011,38(3):5-10.(卢风顺,宋君强,银福康,等. CPU/GPU协同并行计算技术研究综述[J]. 计算机科学,2011,38(3):5-10.) |
| [18] | KIRK D B,HWU W M W. Programming Massively Parallel Processors [M]. Amsterdam:Elsevier,2010. |
| [19] | NVIDIA. NVIDIA’s White Paper of Next Generation CUDA Compute Architecture: Fermi [R]. California:NVIDIA Corporation,2009. |
| [20] | NVIDIA. CUDA: CUFFT Library [S]. California:NVIDIA Corporation,2011. |