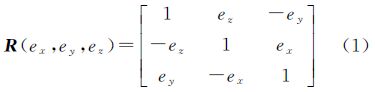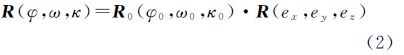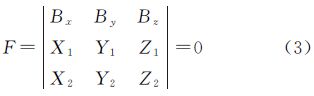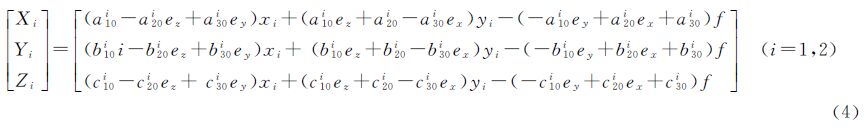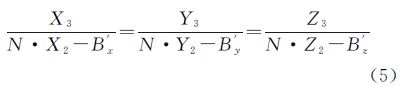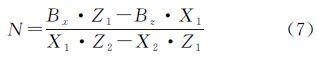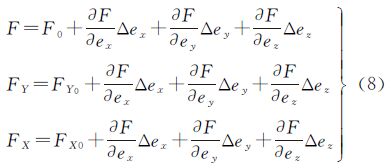1 引 言
惯性测量装置(inertial measurement unit,IMU)由于可以测定运动平台的位置、速度、姿态信息而在航空遥感中得到了广泛应用[1, 2, 3, 4, 5],现已成为许多机载传感器的必备设备,如机载LiDAR、机载三线阵相机、机载SAR等,文献[6—7]介绍了IMU/DGPS系统辅助的机载三线阵影像区域网平差和几何校正。国际上较为有名的两套集成IMU的定位定向系统分别是加拿大的POS AV系统和德国的AERO Control系统,目前国内也已推出了用于车载和机载的定位定向系统。在航空摄影测量中,IMU测定的航空相机的姿态信息,经后处理可转换为像片的外方位角元素[8, 9, 10],为像片外方位元素的确定提供了一种新的方法。然而,由于在安装过程中,IMU的本体坐标轴系与航摄仪的本体坐标轴系不能够保持严格平行,两个坐标轴系之间存在一个小角度的偏差,通常称之为视准轴误差或偏心角误差[11, 12],从而导致 IMU测定的像片外方位角元素不能直接使用,而必须要对其进行视准轴误差的补偿。当前,视准轴误差的求解主要采取飞行检校场的方法,通过对检校场区域获取的像片及观测得到的GPS/IMU等数据的联合平差求得视准轴误差参数。德国IGI公司对AERO Control系统的要求为飞行两条相邻的航线,每条航线10个像对,保证航向重叠和旁向重叠度均为60%,并在检校场的周边布设6个平高控制点。Applanix公司的POS AV系统一般要求检校场为相邻的3~4条航线,每条航线7~12张像片,至少在检校场4角各布设1个平高控制点[3, 12]。然而,对于非区域性、实时性和应急性测绘要求来说,该方法并不适用,而且由于飞行检校场的地形条件、天气原因、飞行时间等与测区不一致,也造成该方法有一定的弊端[13, 14, 15]。文献[16]基于灭点理论提出了一种利用像底点检校IMU视准轴误差的方法,其主要应用于能够提取铅垂线信息的城市大比例尺航空摄影测量,不具有通用性。实际上,获取的航摄像片本身存在固有的几何位置关系,即同名光线对相交的相对定向[17],本文利用这一几何位置关系,将IMU视准轴误差引入立体像对相对定向模型中,提出一种基于相对定向的机载IMU视准轴误差求解新方法,并用试验验证了方法的可行性。
2 相对定向求解IMU视准轴误差的基本数学模型 2.1 视准轴误差航空摄影时,为了利用IMU测定航空相机的姿态,安装时一般将两者固连在一起,并要求IMU本体坐标系与航摄仪本体坐标系的相应坐标轴保持相互平行。只有这样,IMU所测定的姿态角才等同于航摄仪的姿态角。但是,在设备实际安装时,要保证两个坐标轴严格相互平行是很困难的,致使相应坐标轴之间必然会存在一个小的夹角(示意图见文献[5]、文献[9]),可分别用ex、ey、ez表示。考虑到3个夹角均为小角度(<3°),其所构成的旋转矩阵R(ex,ey,ez)可表示为[5]
假定航空摄影时像片的实际外方位角元素为φ、ω、κ,其所构成的旋转矩阵为R,而由IMU直接测定的像片外方位角元素为φ0、ω0、κ0,其所构成的旋转矩阵为R0。顾及视准轴误差所构成的旋转矩阵,三者之间的相互关系可表示为[14]
2.2 单个立体像对的IMU视准轴误差求解模型对于单个立体像对,对其实现正确相对定向后,同名光线会相交在一起,并与空间基线共面,用行列式可表示为[17]
式中,(Bx,By,Bz)为空间基线分量;(Xi,Yi,Zi)(i=1,2)为同名像点的像空间辅助坐标。假设航摄仪的主距为f,航摄像片上量测的像点为(xi,yi),IMU直接测定的像片外方位角元素所构成的旋转矩阵R0(φ0,ω0,κ0)=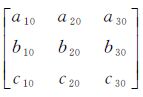 ,结合式(1)、式(2)可得像空间辅助坐标为
,结合式(1)、式(2)可得像空间辅助坐标为
将式(4)代入式(3),即可推导出单个立体像对求解IMU视准轴误差的数学模型。
2.3 连续立体像对的IMU视准轴误差求解模型对于连续立体像对,除了要考虑单个立体模型中同名光线相交的条件外,还要顾及模型之间公共点在前后两个立体模型中所求得的像空间辅助坐标相等的条件。对于一组同名像点,如果在前一个立体模型中计算出的右像片上点投影系数为N,在后一个立体模型中右像片上计算出的像空间辅助坐标为(X3,Y3,Z3),考虑到模型之间的连接条件时应满足[17]
将式(5)变形为
式中,(X3,Y3,Z3)的计算同式(4);(B′x,B′y,B′z)为后一个立体模型中的空间基线分量;点投影系数N的计算公式为
结合2.2节中推导出的单个立体像对求解IMU视准轴误差的数学模型,再将式(4)、式(7)代入式(6)中,即可推导出连续立体像对求解IMU视准轴误差的数学模型。
2.4 求解IMU视准轴误差的误差方程式由于式(3)、式(6)均为非线性方程,在求解未知数时需要先对其进行线性化。考虑到DGPS/IMU系统提供的数据一般经过了后处理,在数据处理中已经过严格的误差模型改正。因此,IMU最终提供的姿态角可为已知值,而摄站坐标主要包含系统性偏移[3],用其计算空间基线(相邻摄站坐标差)时可以消除系统误差,因此,(Bx,By,Bz)也可认为是已知值。在(ex,ey,ez)均为小角度的情况下,设定各未知参数的初值为0,并将式(3)和式(6)按泰勒级数展开取至一次项可得
式中,F0 、FY0、FX0为由未知数初始值按式(3)、式(6)计算出来的结果;Δex、Δey、Δez为视准轴误差ex、ey、ez的改正数;其余各系数为
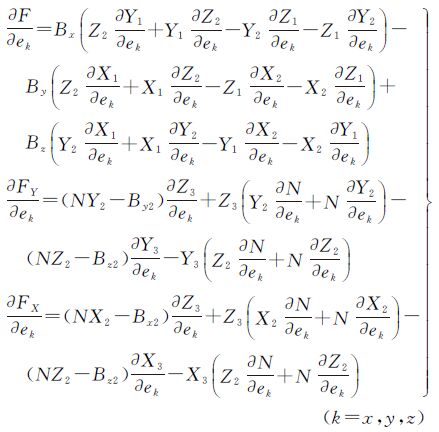
由式(4)、式(7)可得Xi、Yi、Zi、N分别对ex、ey、ez的偏导数为

在实际解算时,首先对量测得到的多组同名像点坐标按式(8)形成误差方程式,然后采用最小二乘方法求解IMU的视准轴误差。
3 试验设计及结果分析 3.1 试验数据简介为了验证本文提出的求解IMU视准轴误差方法的正确性及其求解精度,选择了包括平地、山地、高山地在内的3个地区的带DGPS/IMU系统飞行获取的航空影像进行试验验证(测区基本参数如表 1所示)。航空摄影时,在各试验区内分别架设两台GPS基准站,与机载GPS接收机同步观测,以用于差分GPS数据后处理。飞机在起飞前及落地后都进行了3~5 min的静态观测。
| 项目 | 测区 | ||
| 试验1 | 试验2 | 试验3 | |
| 航摄仪 | Leica RC30 | Leica RC30 | Leica RC30 |
| 航摄仪主距/mm | 153.84 | 303.64 | 154.06 |
| 像幅/(cm×cm) | 23×23 | 23×23 | 23×23 |
| 航摄胶片 | Kodak 2444 | Kodak 2444 | Kodak 2402 |
| 摄影比例尺 | 1∶2500 | 1∶3000 | 1∶32 000 |
| 航向重叠/(%) | 61 | 63 | 64 |
| 旁向重叠/(%) | 32 | 33 | 33 |
| 航线数/条 | 9 | 10 | 9 |
| 构架航线/条 | 2 | 2 | 2 |
| 像片数/张 | 255 | 377 | 244 |
| 地面控制点/个 | 72 | 160 | 34 |
| DGPS/IMU系统 | POS AV 510 | POS AV 510 | POS AV 510 |
| 基准站GPS接收机 | Ashtech | Ashtech | Trimble 5700 |
| 最大地形起伏/m | 38.60(平地) | 181.74(山地) | 729.28(高山地) |
| IMU视准轴误差/arc min | (-8.523,2.626,72.260) | (-7.604,1.971,72.577) | (-8.803,0.116,-1.570) |
航空摄影完成以后,将航摄负片扫描成21 μm的数字化影像,并对GPS/IMU数据用其自带的后处理软件POSPac[18]进行处理,得到每张像片的6个初始外方位元素。为了分析本文求解IMU视准轴误差用于提高直接对地目标定位精度的效果,试验区域内平均每隔2~3条基线布设了一个平高地面控制点,各区域控制点数如表 1所示。然后对数字化影像进行自动量测和转点,控制点的像点坐标经立体量测得到,经粗差剔除后利用相对定向统计的量测精度为6 μm。为了得到IMU的视准轴误差,选择试验区西北角3条航线×7张像片的一个区域作为检校场,将自动量测的影像连接点导入POS AV 510系统自带的检校软件POSCal进行IMU视准轴误差的求解,结果一并列于表 1,将其作为参考值用于分析本文求解方法的结果及精度。
3.2 单个立体像对的求解结果根据2.2节的分析,利用两张像片上同名光线对对相交的几何条件,可以建立求解IMU视准轴误差的误差方程,即式(8)的第一式。为分析用两张像片构成的立体模型求解IMU视准轴误差的效果,从3个试验数据中分别选择3组立体模型进行分析,求解结果如表 2所示。
| arc min | ||||||||
| 试验 | 模型号 | 视准轴误差 | 与参考结果之差 | |||||
| ex | ey | ez | Dex | Dey | Dez | |||
| 1 | 268_267 | -7.296 | 2.317 | 72.607 | -1.227 | -0.055 | -0.347 | |
| 274_273 | -7.475 | 2.613 | 72.304 | -1.048 | -0.351 | -0.044 | ||
| 295_296 | -7.993 | 2.449 | 72.503 | -0.530 | -0.187 | -0.243 | ||
| 2 | 18_17 | -6.186 | 1.715 | 72.306 | -1.418 | 0.256 | 0.271 | |
| 42_43 | -7.394 | 1.653 | 72.776 | -0.210 | 0.318 | -0.199 | ||
| 50_51 | -6.697 | 1.442 | 72.794 | -0.907 | 0.529 | -0.217 | ||
| 3 | 150_149 | -7.943 | 0.279 | -1.857 | -0.860 | -0.163 | 0.287 | |
| 113_114 | -10.643 | 0.275 | -1.588 | 1.840 | -0.159 | 0.018 | ||
| 65_64 | -10.393 | 0.259 | -2.081 | 1.590 | -0.143 | 0.511 | ||
分析表 2中的结果可知,对于3个试验区中的9个立体模型,利用立体模型之间的相对几何关系均可以求解出IMU的视准轴误差,这说明本文所建立的求解IMU视准轴误差的数学模型是正确的。但从求解结果与参考值之差可以看出,ey角和ez角的求解结果较为稳定,而ex角的求解结果对不同的立体模型变化较大,其原因主要是单个立体模型只考虑了同名光线相交的唯一几何条件,即仅仅利用了式(8)中的第一个方程进行求解,立体模型在基线方向上没有约束条件。当立体模型中的两张像片完成相对定向以后,其整体绕左像空间辅助坐标系的x坐标轴旋转对同名光线相交没有影响,而ex角即为沿x坐标轴的旋转角,所以单个立体模型中的几何条件对ex角的约束较弱。此外,由于所获取的摄影基线不可避免会包含一定的偶然误差,在平差解算时这部分偶然误差主要反映在ex角上,不同立体模型的摄影基线中的偶然误差是有差异的,最终造成所求解出的ex角的结果差异较大。
3.3 连续立体像对的求解结果为分析连续立体模型求解IMU视准轴误差的结果,在3个试验区中分别选择不同连续立体模型个数进行试验。在进行IMU视准轴误差求解时,除了考虑单个模型内同名光线的相交,同时顾及模型之间公共点的连接,即同时采用式(8)中3个方程进行计算,结果列于表 3。
| arc min | ||||||||
| 试验 | 模型数 | 视准轴误差 | 与参考结果之差 | |||||
| ex | ey | ez | Dex | Dey | Dez | |||
| 1 | 2 | -7.780 | 2.358 | 72.881 | -0.743 | -0.096 | -0.621 | |
| 3 | -7.770 | 2.193 | 72.943 | -0.753 | 0.069 | -0.683 | ||
| 4 | -8.547 | 2.227 | 72.505 | 0.024 | 0.035 | -0.245 | ||
| 2 | 2 | -7.428 | 1.724 | 72.324 | -0.176 | 0.247 | 0.253 | |
| 3 | -7.393 | 1.773 | 72.764 | -0.211 | 0.198 | -0.187 | ||
| 4 | -7.499 | 2.066 | 72.746 | -0.105 | -0.095 | -0.169 | ||
| 3 | 2 | -9.735 | 0.074 | -1.863 | 0.932 | 0.042 | 0.293 | |
| 3 | -9.409 | 0.052 | -1.893 | 0.606 | 0.064 | 0.323 | ||
| 4 | -9.462 | 0.056 | -1.724 | 0.659 | 0.060 | 0.154 | ||
分析表 3中的结果可知,利用连续立体模型求解IMU视准轴误差时,由于顾及了模型之间公共点的连接,增加了约束条件,求解结果与参考值更加接近。从求解结果与参考值之差可以看出,ey角和ez角的求解结果仍较为稳定,其与参考值的较差也较小,而ex角的求解结果与参考值之差相对稍大。究其原因除了上文所述基线中包含的偶然误差影响外,另外一个主要原因是,表 1中所给的IMU视准轴误差参考值是利用多条航线之间的几何关系,采用基于光束法整体平差思想求解的结果,而本文基于相对定向求解的IMU视准轴误差仅仅利用了单航带内的几何关系,对IMU直接测量的外方位角元素中包含的,沿航线方向上整体侧滚性系统误差则无法消除,该误差最终主要体现在ex角,造成两种方法求解结果相差稍大。但从求解结果来看,本文所提方法是可行的,能够较好地求解出IMU视准轴误差,如要得到更加稳定和精确的结果,必须考虑增加其他约束条件。如参考文献[16],在求解时增加像底点的约束条件,以及参考文献[19]、文献[20],在相对定向中考虑同名直线、曲线等其他特征条件的约束,这些条件必将是对本文方法很好的补充。
3.4 实际定位精度分析视准轴误差求解的目的是用于改正IMU直接测定外方位角元素中的系统误差,进而提高直接对地目标定位的精度。因此,为了分析本文提出的IMU视准轴误差求解方法对提高直接对地目标定位精度的效果,将表 3中所求解出的IMU视准轴误差分别用于改正IMU直接测定的外方位角元素,然后用多片前方交会方法求解像控点的地面坐标,并与外业测量结果进行比较。由于本文主要讨论IMU直接测定的外方位角元素中的系统误差,所以对线元素包含的平移系统误差统一考虑,此外,为了避免坐标转换可能引入的误差,定位计算和结果比较都在WGS-84坐标系下进行,高程采用相对于WGS-84地球椭球的大地高,统计结果列于表 4。
| m | ||||||||||||
| 试验 | 改正误差的模型数 | 最大误差 | 最小误差 | 中误差 | ||||||||
| X | Y | H | X | Y | H | X | Y | H | ||||
| 1 | 无 | -3.703 | 6.314 | -15.747 | 0.019 | 0.134 | -12.249 | 1.514 | 2.834 | 14.614 | ||
| 2 | 0.391 | -0.688 | 0.285 | 0.007 | 0.003 | 0.008 | 0.144 | 0.343 | 0.133 | |||
| 3 | 0.391 | -0.691 | -0.304 | 0.006 | 0.002 | 0.009 | 0.146 | 0.344 | 0.137 | |||
| 4 | 0.315 | -0.684 | 0.274 | 0.007 | -0.001 | -0.004 | 0.149 | 0.345 | 0.124 | |||
| 2 | 无 | 5.113 | -6.638 | -2.581 | -0.003 | -0.007 | 0.002 | 1.840 | 2.833 | 0.839 | ||
| 2 | 0.287 | -0.354 | 0.297 | 0.002 | -0.003 | -0.001 | 0.132 | 0.141 | 0.124 | |||
| 3 | 0.294 | -0.314 | 0.304 | 0.001 | -0.005 | -0.001 | 0.133 | 0.138 | 0.127 | |||
| 4 | 0.265 | -0.244 | 0.298 | -0.001 | 0.003 | -0.002 | 0.122 | 0.103 | 0.124 | |||
| 3 | 无 | -2.210 | 14.829 | 8.204 | -0.055 | -0.080 | 0.108 | 0.910 | 11.135 | 3.953 | ||
| 2 | -1.471 | -2.165 | 1.727 | 0.014 | 0.001 | -0.072 | 0.622 | 1.192 | 0.709 | |||
| 3 | -1.512 | -2.157 | 1.811 | 0.009 | 0.008 | -0.048 | 0.620 | 0.997 | 0.761 | |||
| 4 | -1.518 | -2.263 | 1.843 | 0.036 | -0.011 | -0.026 | 0.625 | 1.035 | 0.769 | |||
比较表 3中的视准轴误差和表 4中的定位结果可以看出,定位误差的大小与系统误差的大小有直接关系,ex角对Y坐标影响较为明显,ey角对X坐标影响较为明显,3个试验区ey角均小于其他两个误差角,因此,在视准轴误差没有得到改正时,定位结果中X坐标方向均小于其他两个方向。当利用本文方法求解的视准轴误差改正外方位角元素后,定位结果得到了较大的提高,然而,由于IMU测定的外方位角元素在飞行方向上包含整体旋转的系统误差,ex角不能得到完全改正,造成Y坐标方向的误差相对较大,这与3.3节中的分析结果相一致。通过分析发现,误差较大的点都仅出现在单航带内,对于出现在相邻两条航带上的点,由于航带的飞行方向相反,系统误差大小基本相等,符号相反,当采用多片前方交会时,误差可以得到一定的抵消。比较利用不同立体模型数改正系统误差后的定位结果可以看出,误差大小没有明显差异,这说明,3张像片构成的两个连续立体模型相对定向时即可将IMU视准轴误差很好地求解出来,如果在求解过程中增加地面约束条件,有望得到更加精确的求解结果。
4 结束语利用航空影像之间的相对几何关系,本文提出了基于相对定向的IMU视准轴误差求解思想,详细推导了基于单个立体模型和连续立体模型求解IMU视准轴误差的数学模型,并用3个实际试验区的数据进行了验证。该方法不涉及检校场和地面控制点,只是利用影像之间固有的相对位置关系,避免了飞行检校场所带来的诸多问题。同时也有利于在线IMU视准轴误差的求解,实现快速实时定位,为基础地理信息的快速获取、更新和各种应急测绘提供保障。但该方法也存在一定缺点,首先是没有考虑相邻航线之间的几何关系,这也是导致ex角求解不稳定的原因之一;其次是本文试验数据针对的是框幅式大面阵模拟像片,而对目前广泛采用的小像幅数码影像,以及航空三线阵数字相机是否适用还有待作进一步试验。
| [1] | MOSTAFA M M R. Camera/IMU Boresight Calibration: New Advances and Performance Analysis [C]//Proceedings of the ASPRS Annual Meeting. Washington DC:[s.n.], 2002. |
| [2] | ALISON K. BROW N. Test Result of a GPS/Inertial Navigation System Using a Low Cost Mems IMU[C]//Proceedings of the 11th Annual Saint Petersburg International Conference on Integrated Navigation System. Saint Petersburg:[s.n.], 2004. |
| [3] | YUAN Xiuxiao, FU Jianhong, ZUO Zhengli, et al. Accuracy Analysis of Direct Georeferencing by Airborne Position and Orientation System in Aerial Photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2006,31(10):847-850.(袁修孝, 傅建红,左正立,等. 机载POS系统用于航空遥感直接对地目标定位的精度分析[J]. 武汉大学学报:信息科学版,2006,31(10):847-850.) |
| [4] | CAI Wenhui, LIANG Guohua. On the Use of IMU/DGPS-assisted Aerial Photogrammetry[J]. Bulletin of Surveying and Mapping, 2009(4):42-43. (蔡文惠,梁国华. IMU/DGPS辅助航空摄影测量应用探讨[J]. 测绘通报,2009(4):41-43.) |
| [5] | LI Xueyou. IMU/DGPS-supported Photogrammetry-Theory, Approaches and Practice[D]. Zhengzhou: Information Engineering University,2005. (李学友. IMU/DGPS辅助航空摄影测量原理、方法与实践[D]. 郑州:信息工程大学,2005.) |
| [6] | LIU Jun, WANG Donghong, LIU Jingxian, et al. IMU/DGPS Supported Block Adjustment of ADS40 Three Line Imagery Data[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(1):55-60. (刘军,王冬红,刘敬贤,等. IMU/DGPS系统辅助ADS40三线阵影像的区域网平差[J]. 测绘学报,2009,38(1):55-60.) |
| [7] | LIU Jun, ZHANG Yongsheng, WANG Donghong, et al. Geometric Rectification of Airborne Linear Array Pushbroom Imagery Supported by INS/DGPS System[J]. Journal of Remote Sensing, 2006,10(1):21-26. (刘军,张永生,王冬红,等. INS/DGPS支持的机载线阵推扫影像几何校正[J].遥感学报,2006,10(1):21-26. ) |
| [8] | FU Jianhong. A Study of Integration of GPS Precise Point Positioning with INS Applied in Aerial Photogrammetry [D]. Wuhan: Wuhan University,2008. (付建红. GPS精密单点定位与INS技术组合用于航空摄影测量研究[D]. 武汉:武汉大学,2008.) |
| [9] | YUAN Xiuxiao, ZHANG Xueping, FU Jianhong. Transformation of Angular Elements Obtained via a Position and Orientation System in Gauss-Kruger Projection Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(3):338-344.(袁修孝,张雪萍,付建红. 高斯-克吕格投影坐标系下POS角元素的转换方法[J]. 测绘学报,2011,40(3):338-344.) |
| [10] | LIU Jun, WANG Donghong, ZHANG Yongsheng. Analysis and Transformation between HPR and OPK Angles of the GPS/INS System[J]. Science of Surveying and Mapping, 2006, 31(5):54-56. (刘军,王冬红,张永生. GPS/INS系统HPR与OPK角元素的剖析与转换[J]. 测绘科学,2006,31(5):54-56.) |
| [11] | LI Xueyou, NI Zhongli. Research on Calibration Field Designing for IMU/DGPS Supported Photogrammetry[J]. Engineering of Surveying and Mapping, 2005,14(4):14-18. (李学友,倪忠礼. IMU/DGPS辅助航空摄影测量中检校场布设方案研究[J]. 测绘工程,2005,14(4):14-18.) |
| [12] | FU Jianhong. Research on Calibration Field Designing for Airborne Position and Orientation System[C]//Proceedings of the International Society for Optical Engineering.[S.l.]:SPIE, 2009. |
| [13] | YUAN Xiuxiao. A Novel Method of Systematic Error Compensation for a Position and Orientation System[J]. Progress in Natural Science, 2008,18(8):925-934. (袁修孝. 一种补偿POS定位测姿系统误差的新方法[J]. 自然科学进展,2008,18(8):925-934.) |
| [14] | MADANI M, MOSTAFA M M R. ISAT Direct Exterior Orientation QA/QC Strategy Using POS Data[C]//Proceedings of OEEPE Workshop on Integrated Sensor Orientation. Hanover:[s.n.], 2001. |
| [15] | RESSL C. The OEEPE Test “Integrated Sensor Orientation” and Its Handling with the Hybrid Block Adjustment Program ORIENT[C]//Proceedings of OEEPE Workshop on Integrated Sensor Orientation. Hanover:[s.n.], 2001. |
| [16] | FU Jianhong, ZHAO Shuangming. Boresight Misalignment Calibration of Airborne Position and Orientation System Based on Photo Nadir Point[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(5):610-615.(付建红,赵双明. 基于像底点的机载POS视准轴误差检校[J]. 测绘学报,2011,40(5):610-615.) |
| [17] | LI Deren, ZHENG Zhaobao. Analytical Photogrammetry[M]. Beijing: Publishing House of Surveying and Mapping, 1992. (李德仁,郑肇葆. 解析摄影测量学[M]. 北京:测绘出版社,1992.) |
| [18] | Applanix Product Outline. POSPacTM Air[EB/OL]. [2012-09-08].http://www.applanix.com/products/airborne/pospac-mms.html, 2012. |
| [19] | ZHANG Yongjun, HU Binghua, ZHANG Jianqing. Relative Orientation Based on Multiple Conjugate Features[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(2):194-199.(张永军,胡丙华,张剑清. 基于多种同名特征的相对定向方法研究[J]. 测绘学报,2011,40(2):194-199.) |
| [20] | ZHANG Jianqing, ZHANG Hongwei, ZHANG Zuxun. Exterior Orientation for Remote Sensing Image with High Resolution by Linear Feature[C]//Proceedings of the Internatinal Archives of the Photogrammetry, Remote Sensing and Spatial Information Science. Istanbul: ISPRS, 2004:1-4. |