1 引 言
海洋卫星测高技术是20世纪70年代发展起来的一种新型的卫星遥感测量技术,随着空间技术、光电技术和微波技术等高新技术的发展,在空间大地测量领域产生了一场深刻的革命。卫星测高提供了海洋区域统一的高程基准,高精度、高分辨率的大地水准面起伏,以及全球海域高精度、高分辨率的重力异常。
目前,已有Geosat、ERS-1、ERS-2和T/P等主要测高卫星的资料,以及正在运行的主要接替卫星Envisat、Jason、GFO、Cryosat2也可利用,并将陆续发射Altika、HY-2B和SWOT等新一代测高卫星。利用目前多颗测高卫星的融合,已获得全球海洋区域2′×2′分辨率及毫伽级精度的海洋重力场分布[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14],这已是现有传统高度计观测模式下反演海洋重力场的极限。
随着卫星测高资料的不断补充和积累,以及新数据处理手段的提出和改进,卫星测高技术的研究和应用领域将得到进一步拓宽和深化。就大地测量领域而言,利用卫星测高资料反演重力异常的主要工作,将着重于更高精度和高分辨率以及时变重力场的确定。
依靠单颗测高卫星同时满足反演全球高精度和高分辨率海洋重力场的要求,需要很长时间的高精度海面高度观测积累,以实现卫星轨道交叉点高密度的要求(在由逆Vening-Meinesz公式反演海洋重力场过程中,海洋重力场由沿轨海面高梯度计算的轨道交叉点垂线偏差资料得到。因此,测高海洋重力场的空间分辨率主要是由轨道交叉点的空间分布决定的)。对于这种长重复周期的卫星轨道,经过卫星轨道交叉点的升轨和降轨时间间隔可能相差几个月,甚至几年。考虑到长时间间隔情况下,复杂的星下点海面变化,卫星升降轨海面高梯度观测精度已不能满足轨道交叉点高精度垂线偏差计算的需要。为提高测高反演海洋重力场的空间分辨率和精度,国内外许多学者通过联合多颗测高卫星观测结果进行重力场反演计算,其主要目的是为了提高轨道交叉点的分布密度,缩短经过轨道交叉点不同沿轨海面高梯度的时间间隔。但从卫星测高技术的发展历程来看,绝大多数卫星高度计主要用于海洋动力环境监测研究,只有Geosat的GM(geodetic mission)任务和ERS-1的168天重复周期任务是为了实现测高反演海洋重力场--这一大地测量学研究内容而设计的。现有的测高反演海洋重力场结果中,其高频/短波部分主要依靠Geosat/GM和ERS-1/168days期间的观测数据。这两颗测高卫星,分别与20世纪80年代和90年代初期在轨运行,受当时技术条件的限制,轨道确定精度和高度计的观测精度都无法满足高精度重力场反演的要求,同时两颗卫星交叉点的空间覆盖也满足不了高分辨率(优于2′×2′)的要求。
在国外测高高度计发展过程中,实际上也有双星伴飞模式的雏形,例如Topex/Poseidon和Jason-1两颗卫星在轨重叠任务期间,进行了双星伴飞的组合试验,其主要目的是为了两颗高度计观测资料的数据标定/校验,以及提高中尺度海洋动力环境的监测能力。但通过这样的两颗卫星组合方式,已证明了双星伴飞模式可以用来提高数据观测的空间分辨率。
同时,新的测高观测技术也正用于提高测高重力场反演精度和分辨率中,例如,美国宇航局(NASA)提出利用先进的干涉合成孔径高度计实现对星下点海平面的扫描式观测,以大幅缩短单颗卫星全球覆盖的重复周期,进而提高交叉点垂线偏差的计算精度。欧空局(ESA)计划利用新型合成孔径高度计技术提高沿轨海面高及海面高梯度的观测精度。除了多颗测高卫星的观测组合,以及新型高度计(合成孔径高度计、干涉合成孔径高度计等)的应用之外,还有许多学者对测高数据处理技术进行了深入探讨,发展诸如波形恢复技术等方法[15, 16],以提高卫星测高海面高观测精度。
本文在已有的卫星高度计精度指标基础上,根据测高卫星轨道设计的基本要求,以及测高重力场反演重力场空间分辨率的需求,笔者提出一种双星伴飞模式的测高卫星轨道设计方案。并给出相应的轨道设计,利用该方案,可在较短时间内,实现高分辨率全球大部分海域的海面高梯度测量,为海洋测高重力场的精确确定提供了高分辨率的数据。可将测高反演海洋重力场的分辨率提高到1′×1′。
2 测高卫星的双星伴飞模式卫星测高双星伴飞模式,是指为满足提高反演海洋重力场空间分辨率以及海平面高梯度计算精度的要求,采用类似于Topex/Poseidon和Jason1组合的卫星轨道运行模式,见图 1。其主要思想是,两颗卫星采用相同的轨道参数,仅在入轨时,在赤道上空,东西间隔2 km。在两颗卫星有效观测期间,两颗卫星始终同时处于相同纬度。仅经度方向上有固定的距离。这样处理的优点在于对海平面高度进行测量时,可以同时给出星下点海平面东西方向和南北方向上的梯度值。而且由双星模式计算的海面高梯度的精度优于传统单颗卫星得到的结果。

|
| 图 1 测高卫星的双星伴飞模式设计 Fig. 1 Twin-satellites altimetry design |
这种双星伴飞模式将具有如下优点。
(1) 太阳同步轨道:可以避免太阳能帆板的转动对姿态的影响。
(2) 空间覆盖:全球绝大部分海域,空间分辨率高,卫星寿命期间可以实现多次覆盖。
(3) 双星组合:实时计算星下点海面高梯度,包括南北方向和东西方向。通过双星组合,可以大幅提高计算精度。
(4) 反演重力场方法:既可以利用海面高度观测,也可以利用海面高梯度信息反演海域重力场。
(5) 降低地球物理改正项的要求:利用海面高梯度反演重力场,通过双星位置的关系与地球物理改正时空特征,可以降低地球物理改正的要求。
(6) 可快速形成多种分辨率的重力场产品:得益于双星伴飞模式的优点,可以利用不同时间段的卫星观测资料反演不同分辨率的重力场,可以进行重力场时变监测,可以监测全球海平面变化。
3 双星伴飞模式测高卫星轨道设计 3.1 轨道需求分析为满足卫星高度计的任务需求,卫星经过同一地区时的光照条件应基本一样,星下点轨迹应周期性重复,故应选择太阳同步兼回归轨道。为满足全球南北纬度±80°的覆盖观测范围,决定了轨道倾角应在90°~100°之间。考虑到星载仪器的工作环境要求,以及其他因素。卫星轨道高度设定在800 km左右。
在高度及资料反演重力场过程中,由于轨道设计通常采用近似极轨的方式运行,因此高度计计算的海面高梯度中,南北方向上海面高梯度分量计算精度明显优于东西方向上梯度分量计算精度。为提高重力场反演精度。理论上,应尽可能采用类似T/P或Jason-1/2的近似66°倾角的观测轨道。但考虑到太阳同步设计和轨道高度的要求,双星伴飞模式的卫星轨道设计采用大约98°的倾角。
3.2 轨道设计计算卫星的运行轨道由轨道倾角i、近地点幅角ω、升交点赤经Ω、偏心率e、轨道半长轴a 以及卫星经过近地点的时刻tp共6个经典轨道要素决定。只要确定了某一时刻的卫星轨道6要素,卫星的轨道即卫星的位置和速度矢量也就确定了。其中,i<和 Ω决定了轨道面在惯性空间的位置;ω决定了轨道本身在轨道面内的指向;a和e决定了轨道的大小和形状;tp决定了卫星在轨道上的位置[17, 18, 19]。
太阳同步轨道卫星的轨道平面绕地球极轴进动的角速度,等于地球绕太阳公转的平均角速度(0.985 647°)。实现太阳同步,可使太阳矢量与轨道平面的夹角基本保持不变。太阳同步轨道的主要优点是卫星的降交点地方时基本保持不变,卫星每天可在相同的光照条件下定时获取相应地区的观测资料。卫星太阳同步轨道特性利用了地球形状摄动中的主要部分J2项,使卫星轨道Ω的长期变化率等于地球绕太阳公转的平均角速度,从而实现太阳同步。在地球非球形J2项摄动的影响下,升交点赤经的长期变化率为
式中,Re为地球赤道平均半径,且Re=6 378.137 km;n为轨道平均角速度。在太阳同步条件下,近地轨道的轨道倾角与半长轴应有如上相互约束的条件。
冻结轨道使卫星地面高度在同一地区几乎保持不变,轨道的拱线静止,即轨道半长轴指向不变。冻结轨道的形状保持不变,亦即ė= =0,这可通过相应的小偏心率和对ω进行约束而实现。考虑J2、J3项,并把摄动函数代入拉格朗日摄动方程,则有
=0,这可通过相应的小偏心率和对ω进行约束而实现。考虑J2、J3项,并把摄动函数代入拉格朗日摄动方程,则有
由式(2)、式(3)可知:当i<=63.4°时,(1-5/4sin2 i<)=0,则dω/dt和de/dt均为0,此即临界倾角;当ω=90°、270°时,de/dt=0。因此,在设计冻结轨道参数时,应先根据太阳同步轨道的要求,选择半长轴a和轨道倾角i,再由ω=90°、270°,得de/dt=0。根据冻结轨道的定义,此时还应有dω/dt=0。由式(2)可得
因为J3<0,所以当tan2 i>e时,ω = 90°;当tan2 i<e时,ω=270°。因此,对高度低于1000 km的近地轨道,只有当i<2°时,才有ω=270°,在其余倾角下均取ω=90°。整理式(4),略去e的高阶小量,并代入ω=90°,可得
由式(5)可知,冻结轨道的偏心率e取决于半长轴a和轨道倾角i。
降交点地方时的选取考虑两种因素,一是对光照和阴影区的要求;二是太阳引力对卫星的摄动,特别是对轨道倾角的摄动影响。影响降交点地方时TDN主要有太阳引力引起i的变化,以及大气阻力引起Ω的改变两个因素。若TDN=6:00或18:00时,则轨道平面大致与太阳射线垂直;若TDN=12:00或0:00时,则轨道平面大致与太阳射线平行。
升交点赤经为春分点至轨道升交点的角距。太阳同步轨道Ω 一年的变化量为360°,在地球J2项的作用下,Ω 的变化率接近于0.985 6°/d。在发射时间和降交点地方时确定后,发射点的Ω也就相应确定了。如发射选在春分日,则当TDN为0:00时,该点的Ω=180°;当TDN为6:00时,该点的Ω=90°;当TDN为12:00时,该点的Ω=0°;当TDN为18:00时,该点的Ω=270°。
常用的轨道周期有恒星周期Ts和交点周期Tφ。因卫星轨道在不断变化,对应瞬时轨道的周期亦随时间t而变。恒星周期Tφ为
式中,μ 为地球引力常数。
恒星周期是理想的周期,未计入摄动对轨道的影响,而且它无法直接测定。但卫星在实际运行时,会受到多种摄动的影响,尤其是由地球非球形J2项摄动引起的卫星轨道升交点赤经的长期变化,会使卫星星下点轨迹的升交点在赤道上产生漂移。交点周期Tφ是对应卫星星下点连续两次(升段或降段)通过同一标准纬圈φ的时间间隔。Ts与Tφ存在以下关系
式中,交点周期Tφ主要取决于半长轴a,受轨道倾角i的影响较小。
3.3 双星伴飞模式卫星高度计轨道参数根据对卫星轨道应用的初步分析,星下点轨迹应周期性地重复,因此轨道设计需要选择太阳同步回归轨道。卫星轨道设计过程中,可以根据项目的实际情况,选择多个轨道的高度H和倾角i以满足既定约束条件,再从这些轨道中挑选出满足要求的轨道。测高高度计卫星计划同时发射两颗卫星,目标是实现1′×1′ 重力场空间分辨率,因此,双星组合的空间覆盖分辨率需优于1′×1′,考虑到卫星沿轨速度通常在7 km/s左右,传统模式下高度计观测沿轨频率通常高于每秒20次,20 Hz的高度计沿轨观测间隔约为350 m。如果高度计采用SAR(synthetic aperture radar)模式,通过多视观测,沿轨空间分辨率约为320 m[参考Cryosat2 SAR/SARin(synthetic aperture radar interfere)模式]。此外,考虑到卫星设计倾角选择90°~100°的太阳同步轨道,因此,双星组合在沿轨方向上(或转换成子午线方向上)的空间分辨率可以满足重力场反演的需要。在东西方向上,当采用设计轨道,相邻卫星观测轨迹间距在赤道上小于1′ 时,即可满足空间分辨率的要求。轨道空间分辨率设计的关键在于,如何设计一种双星观测模式,使得卫星轨迹在赤道上的相邻轨迹间距优于1′(1海里)。同时,这样的轨道回归周期需尽可能短,轨道倾角需尽量避免极轨。避免极轨的原因是为了在由高度计资料计算海平面梯度时,尽可能提高东西方向上海平面梯度的观测精度[8]。不同轨道倾角东西方向、南北方向海平面梯度示意见图 2。

|
| 图 2 同轨道倾角东西方向、南北方向海平面梯度示意图 Fig. 2 Components of deflections of verticals vs. inclination |
由于采用双星同时观测,通过双星组合,对其中任意一颗卫星,只需满足赤道上相邻轨道间距优于2′,再通过另一颗卫星的空间覆盖补充(类似T/P和Jason1项目标定期间的组合模式),即可实现赤道上1′轨道间距的要求。
为此,可先给出回归圈数N,再由N计算出回归周期D,然后在多种组合中选择合适的轨道倾角i,根据a和i关系,通过解方程可得到轨道的高度。
回归圈数计算:对要求实现全球覆盖的对地观测卫星,从轨道设计的角度来说,其回归圈数和回归周期的确定可分成两种情况。一是回归圈数取决于有效载荷的对地观测带宽。假设对地观测卫星的观测带宽为K km,重叠率为η,则实现全球覆盖一个回归周期内的回归圈数N = 2πRe/K(1-η)。回归周期和回归圈数确定后,再根据冻结轨道和太阳同步轨道对轨道高度、偏心率和轨道倾角的约束条件,筛选出符合条件的轨道6要素。二是根据执行任务的时间要求,以及轨道高度、回归周期和回归圈数的约束,确定轨道参数。
当Re取6 378.137 km;K取2′(约3.6 km);η为轨道刈幅重叠率,考虑到无论是传统LRM(low resolution mode)模式还是SAR模式的高度计观测,其单点观测的星下点足迹宽度都超过2 km,因此在计算回归周期时,η可设为0,通过计算可得N=10 800。即两颗高度计卫星各需围绕地球观测10 800圈,再通过数据融合处理,即可实现全球海平面1′×1′ 空间分辨率的观测。
回归周期计算:回归圈数确定后,再根据回归圈数N,以及半长轴a、交点周期Tφ等约束条件,可以确定回归周期D。回归轨道是指地面轨迹经过一段时间后出现重复的轨道。取卫星交点周期Tφ的单位为h,若存在互质的正整数D 和N,满足24/Tφ=N/D,则经过D天后,绕地球转过的圈数为N。此处,D被称为回归周期,N为一个回归周期内的回归圈数。若N=1,则表示每天回归的轨道。卫星回归轨道的条件也可表示为
式中,ωe为地球自转的角速度;dΩ/dt为轨道升交点赤经进动的角速度。回归轨道不一定是太阳同步轨道。
综合考虑卫星设计寿命、大气阻力、电离层等各种因素,高度计卫星的轨道高度大致设定在800 km左右。在太阳同步轨道的前提下,轨道高度越高,可以获得更好的轨道倾角。由轨道高度与交点周期的关系可知,800 km高度的卫星轨道,其轨道交点周期Tφ大致约为6060 s,由此可先估算D值的大小。
ωe为地球自转的角速度(ωe=7.292 115 146 7×10-5rad/s,实际计算中需要转换成rad/d);dΩ/dt为轨道升交点赤经进动的角速度(dΩ/dt=1.990 968 183 8×10-7rad/s,实际计算中需要转换成rad/d) 通过计算,可取D值757,即设计轨道回归周期757 d,可证明,回归圈数10 800圈和回归周期757 d互质(此处,略去证明步骤)。则一天内卫星运行的圈数为14 202/757圈。轨道交点周期精确计算:当已知回归圈数和回归周期后,即可精确计算轨道交点周期,有Tφ=6056 s,即轨道绕地球运行一圈的时间为6056 s。
轨道高度精确计算:由恒星周期、轨道交点周期和太阳不同轨道条件公式,有
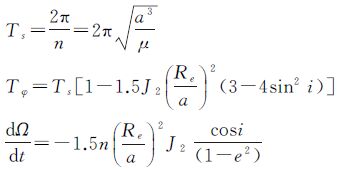
已知Tφ=6056 s,则解上述方程可求出 a-Re,即轨道高度为796.795 km。 上述方程式的解算可以利用Mathmatics软件或采用数值逼近方法解算。
轨道倾角计算:由太阳同步轨道条件可由计算所得轨道高度,通过式(1)计算轨道倾角:当轨道高度为796.795 km时,轨道倾角i=98.589 2°。
轨道偏心率计算:根据冻结轨道条件,式(5)可得偏心率e=0.001 028 87;式中,J3取-2.534 553 38E-006。
考虑到卫星的工作寿命较长(至少5年),轨道设计计算中考虑了地球的二阶长期摄动。兼顾了太阳同步、回归,全球覆盖3种轨道特性,表 1给出了卫星和轨道设计有关的卫星总体参数。
| 轨道参数 | 大地测量任务期间 |
| 轨道类型 | 椭圆形、太阳同步 回归、全球覆盖 |
| 轨道长半轴/km | 796.795+6 378.137 |
| 轨道平均高度/km | 804 | 轨道倾角/(°) | 98.589 2 |
| 交点周期/s | 6056 |
| 偏心率 | 0.001 028 87 |
| 回归周期/d | 757 |
| 回归圈数/圈 | 10 800 |
| 每天运行圈数/圈 | 14+202/757 |
| 近地点幅角/(°) | 90 |
| 降交点地方时 | 6:00am |
| 地面分辨率/km | 南北向<2 km 东西向大约2 km |
| 地面覆盖范围/(°) | 81.410 8S~81.410 8N |
根据表 1的轨道参数,经仿真分析,可计算出如下的星下点轨迹图(图 3-图 6),并表明轨道方案中的轨道具有良好的回归特性。

|
| 图 3 单星1 d地面轨迹示意图 Fig. 3 Ground track in one day of new mode |

|
| 图 4 单颗卫星5 d地面轨迹分布图 Fig. 4 Ground track in five days of new mode |

|
| 图 5 单颗卫星15 d地面轨迹分布图 Fig. 5 Ground track in fifteen days of new mode |

|
| 图 6 单颗卫星30 d地面轨迹分布图 Fig. 6 Ground track in thirty days of new mode |
从卫星地面轨迹分布来看,对双星伴飞模式测高卫星中任意一颗卫星,每天至少有4 d升轨和降轨通过我国海域。测高卫星的有效观测范围覆盖了全球海洋绝大部分区域,在极区也有部分观测值。卫星轨道空间分布大致均匀,从15 d和30 d卫星地面轨迹分布图来看,利用15 d和30 d大致全球均匀分布的观测数据,就可以得到全球较低分辨率的海面高观测结果。粗率估算,在一个完整的回归周期757 d内,大约可实现2.6×109个独立的海面高观测,在2 km×2 km单元格内,约有22个观测数据。这样密集的数据采样,为实现高分辨率和高精度的海洋重力场反演提供了基础数据。可估算,卫星正常运行N天即可获得较低分辨率的重力场。卫星运行周期和反演海洋重力场分辨率见表 2。
| 卫星运行天数/d | 重力场产品 |
| 30 | 30 min×30 min |
| 90 | 10 min×10 min |
| 180 | 5 min×5 min |
| 365 | 2 min×2 min |
| 757 | 1 min×1 min |
根据测高卫星轨道设计的基本要求,以及测高重力场反演重力场空间分辨率的需求,笔者提出的测高卫星轨道设计方案可在较短时间内,实现高分辨率全球大部分海域的海面高梯度测量,为海洋测高重力场的精确确定提供了高分辨率的数据。与传统单星测高模式相比,双星伴飞模式的测高卫星不仅能提供双星星下点海面高度的信息,其最大的优势还在于能够实时给出星下点海面梯度观测信息,这是传统单星测高模式无法比拟的。
该测高卫星轨道对海洋重力场反演精度的影响,主要体现在获取的星下点海平面梯度数据精度的提升上面。传统测高反演海洋重力场中,在轨道交叉点上,可以利用升轨和降轨的沿轨迹海面高梯度两个观测量来解算交叉点处的垂线偏差,在非交叉点上,通过不同卫星的数据累积,或者通过相邻交叉点上解算值的内插,获得沿轨垂线偏差计算值。双星伴飞模式的测高卫星不仅能提供星下点海面高度信息,还可以实时给出星下点海面梯度观测信息,与传统测高模式相比,大大提高了海面梯度观测分布密度和精度。进而,由海平面梯度信息推算的海洋重力场结果(包括垂线偏差、重力异常等)的精度也会得到提高。
在双星伴飞模式测高卫星数据处理过程中,由于各项地球物理改正项在小尺度空间范围内,变化都比较平缓,通过差分的方法,可以有效地降低地球物理改正对最终梯度计算的影响。另外,由于两颗卫星星间距始终保持在一定范围内(大约2 km),因此,两颗卫星数据处理过程中,各项大气、地球物理改正项也几乎一致。当采用海面高梯度方法通过逆 Vening-Meinesz公式反演海洋重力场时,可以降低高度计数据处理过程中各项大气、地球物理项改正的精度要求。
| [1] | FU L L, CAZENAVE A. Satellite Altimetry and Earth Sciences: a Handbook of Techniques and Applications[M]. San Diego: Academic Press, 2001. |
| [2] | FAIRHEAD J D, GREEN C M, ODEGARD M E. Satellite-derived Gravity Having an Impact on Marine Exploration[J]. Leading Edge, 2001, 20: 873-876. |
| [3] | ANDERSEN O B, KNUDSEN P. Global Marine Gravity Field from the ERS-1 and GEOSAT Geodetic Mission Altimetry[J]. Journal of Geophysics Research, 1998, 103: 8129-8137. |
| [4] | ANDERSEN O B, KNUDSEN P. The DNSC08 Mean Sea Surface and Mean Dynamic Topography[J]. Journal of Geophysics Research, 2009. |
| [5] | HWANG C, PARSONS B. An Optimal Procedure for Deriving Marine Gravity from Multi-satellite Altimetry[J]. Geophysical Journal International, 1996, 125: 705-719. |
| [6] | HWANG C. Analysis of Some Systematic Errors Affecting Altimeter Derived Sea Surface Gradient with Application to Geoid Determination over Taiwan[J]. Journal of Geodynamic, 1997, 71: 113-130. |
| [7] | SANDWELL D T, SMITH W H F. Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J]. Journal of Geophysics Research, 1997, 102: 10039-10054. |
| [8] | SANDWELL D T, SMITH W H F. Retracking ERS-1 Altimeter Waveforms for Optimal Gravity Field Recovery[J]. Geophysical Journal International, 2005, 163, 79-89. |
| [9] | SANDWELL D T, SMITH W H F. Global Marine Gravity from Retracked Geosat and ERS-1 Altimetry: Ridge Segmen-tation Versus Spreading Rate[J]. Journal of Geophysics Research, 2009, 114, B01411, DOI:10.1029/2008 JB006008. |
| [10] | LI Jiancheng, CHEN Junyong, Ning Jinsheng, et al. Theory of Earth Gravity Field Approach and Determination of China Quasi-geoid 2000[M]. Wuhan: Wuhan University Press, 2003. (李建成,陈俊勇,宁津生,等. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉:武汉大学出版社,2003.) |
| [11] | XU Houze, WANG Haiying, LU Yang, et al. Geoid Undulations and Gravity Anomalies from T/P and ERS-1 Altimeter Data in the China Sea and Vicinity[J], Chinese Journal of Geophysics, 1999, 42(4): 465-471. (许厚泽, 王海瑛, 陆洋,等. 利用卫星测高数据推求中国近海及邻域大地水准面起伏和重力异常研究[J]. 地球物理学报, 1999, 42(4): 465-471.) |
| [12] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 179-184. (黄谟涛, 翟国君, 管铮,等. 利用卫星测高数据反演海洋重力异常研究[J], 测绘学报,2001, 30(2): 179-184.) |
| [13] | LI Jiancheng, NING Jinsheng, CHEN Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/ Poseidon, ERS2 and Geosat Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 197-202. (李建成, 宁津生, 陈俊勇,等.联合TOPEX/ Poseidon, ERS2 和Geosat卫星测高资料确定中国近海重力异常[J]. 测绘学报,2001, 30(3): 197-202.) |
| [14] | JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723-729.(金涛勇,李建成,姜卫平,等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报,2011, 40(6): 723-729.) |
| [15] | WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729-734. (汪海洪,罗志才,杨元德,等.基于波形分类的近海卫星测高数据自适应重跟踪方法[J].测绘学报,2012, 41(5): 729-734.) |
| [16] | VIGNUDELLI S, KOSTIANOY A G, CIPOLLINI P, et al. Coastal Altimetry[M]. Berlin: Springer, 2011. |
| [17] | XI Xiaoning, WANG Wei, GAO Yudong. Fundamentals of Near-earth Spacecraft Orbit[M]. Changsha: National University of Defense Technology Press, 2003. (郗晓宁,王威,高玉东. 近地航天器轨道基础[M]. 长沙:国防科技大学出版社,2003.) |
| [18] | LIU Lin. Orbit Theory of Spacecraft[M]. Beijing: National Defence Industry Press, 2000. (刘林,航天器轨道理论[M]. 北京: 国防工业出版社,2000.) |
| [19] | CARL W. A Program of Geosat Exact Repeat Mission[J]. Journal of the Astronautical Sciences, 1991, 39(3): 313-326. |










