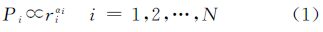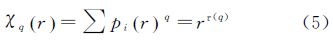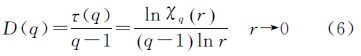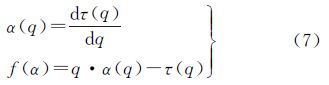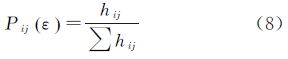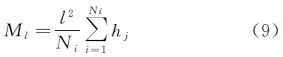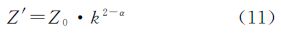1 引 言
地磁导航是一种全天时、全天候、无积累误差的无源自主导航方式。作为一种辅助导航手段,地磁导航在飞行器、船舶等运载体的导航过程中发挥着重要的作用。相对于随空间位置变化缓慢的地球主磁场,地磁异常场在局部区域内变化复杂,在小尺度下具备较强的奇异性,它更适合作为地磁导航的参考场。作为一种辅助导航方式,地磁匹配的精度决定了地磁导航的可靠程度,而它又直接依赖于地磁基准图的准确性。但是受成本、时间等因素的制约,实际中直接磁场测量的结果往往分布范围小或空间分辨率较低,因而在实测数据基础上准确的重构区域地磁异常场成为地磁导航的关键[1, 2, 3]。
许多学者对构建地磁导航基准图作了相关研究:文献[4]采用BP神经网络预测未知位置的地磁数据,由于在模型训练中输入变量的维数过低,导致模型的可靠性较差,随着实际应用中训练样本的减少,模型的预测能力将大大下降;克里金法是一种最优、无偏的地质学统计方法,它充分考虑地磁数据的空间相关性,文献[5]和文献[6]分别使用普通克里金法和泛克里金法进行地磁基准图的构建;文献[7]则提出一种支持向量机-克里金插值算法,采用最小二乘支持向量机从实际资料场中拟合重构变异函数。这些方法能够较好地拟合地磁异常场的整体趋势,但它们的共同缺陷是无法对奇异性较强的局部区域进行准确刻画,这种误差甚至可达到数十nT,严重降低了地磁匹配的可靠性。针对传统构图方法在地磁异常变化较强烈区域的局限性,本文将分形理论引入地磁基准图的构建当中,有效地增强了对小尺度子集的奇异性刻画。
分形理论是由Mandelbrot在20世纪70年代为表征复杂图形和复杂过程首先引入自然科学领域的,用来表征图形的自相似性[8],多重分形理论可以对复杂空间变量的多层次结构进行描述[9]。文献[10]在分析航磁功率谱特征的过程中,表明磁异常具有分形特征;文献[11]建立了描述航磁数据的分形随机模型,有效增强了对地质岩性和磁异常的表达;文献[12]对我国南海磁异常进行了分形特征分析,进而解释其地质结构;文献[13]通过提出基于标准偏差的自适应方法,提高了确定随机分形无标度区间的性能和效率。而这些研究均是对已有数据进行整体上的分形特征描述和分析,而如何在不同尺度上对这种分形特征进行定量描述,并应用到对磁异常局部细节特征的表达上,当前还鲜有研究。本文首先对实测地磁异常数据进行了多重分形谱分析,通过确定标度不变性尺度范围,对分形特征给出多层次定量描述。进一步,根据地磁异常在小尺度范围内的标度不变性,将多重分形理论和克里金法相结合,提出逐步插值校正法制备基准图,试验验证该方法能够完好地刻画地磁异常场在细节上的奇异特征,相对于克里金法、改进谢别德法等传统方法具有明显的优越性。
2 多重分形谱分析方法 2.1 多重分形谱多重分形也称为分形测度,是定义在分形上的多个标度指数的奇异测度所组成的无限集合,采用多个维数来描述非均匀复杂集合体的整体特征。
设F是d维欧式空间的一个子集,测度为μ,把F,μ划分为N个单元Si,Si的尺度为ri,测度(概率)为Pi,且∑Pi=1,对于其中任一单元可用不同的标度指数αi来表征,见式(1)
当尺度大小趋于0时,式(1)可化为
式中,αi又称为奇异性指数,控制着概率密度的奇异性,它反映了相应区域上概率的大小。
把研究对象划分为一系列的子集,使得每一个子集中的小单元都具有相同的α值,子集内的单元数为Nα(r),它和r具备以下关系
由此可得
式中,f(α)的物理意义是表示具有相同α值的子集的分形维数,称为多重分形谱。
从信息论的角度,定义统计矩函数
式中,q∈-∞,∞为统计矩的阶,用来表征多重分形的不均匀程度。当q>0时,主要反映较大概率子集的分形特征;当q <0时,则主要反映较小概率子集的分形特征。对于给定的阶q,τ(q)称为质量指数函数,它是分形行为的特征函数。若τ(q)关于q是一条直线,则研究对象是单分形的;若τ(q)关于q是凸函数,则研究对象有多重分形特征。
定义广义分形维数
D(q)是随不同的q值而有不同的分形维数。
广义分维和多重分形谱满足勒让德变换
2.2 不规则空间变量分析方法对于规则分形集,可以直接通过统计物理方法进行多重分形谱的分析,但是对于不规则分形集,一般都是通过盒计数法求出物理量的概率分布,然后借助统计物理原理进行多重分形谱分析[10, 11]。
对于N×N的二维粗糙表面数据集,令研究区域边长为1,用边长为ε(ε≤1)的正方形盒子覆盖整个区域,以研究数据集的衬底表面为基准,可求得第(i,j)个小盒子中的概率,如式(8)
式中,hij表示第(i,j)个盒子内的平均高度,通过改变ε的取值,可得用不同尺度的盒子覆盖研究数据集时的概率分布,本方法能较好地满足标度不变性。
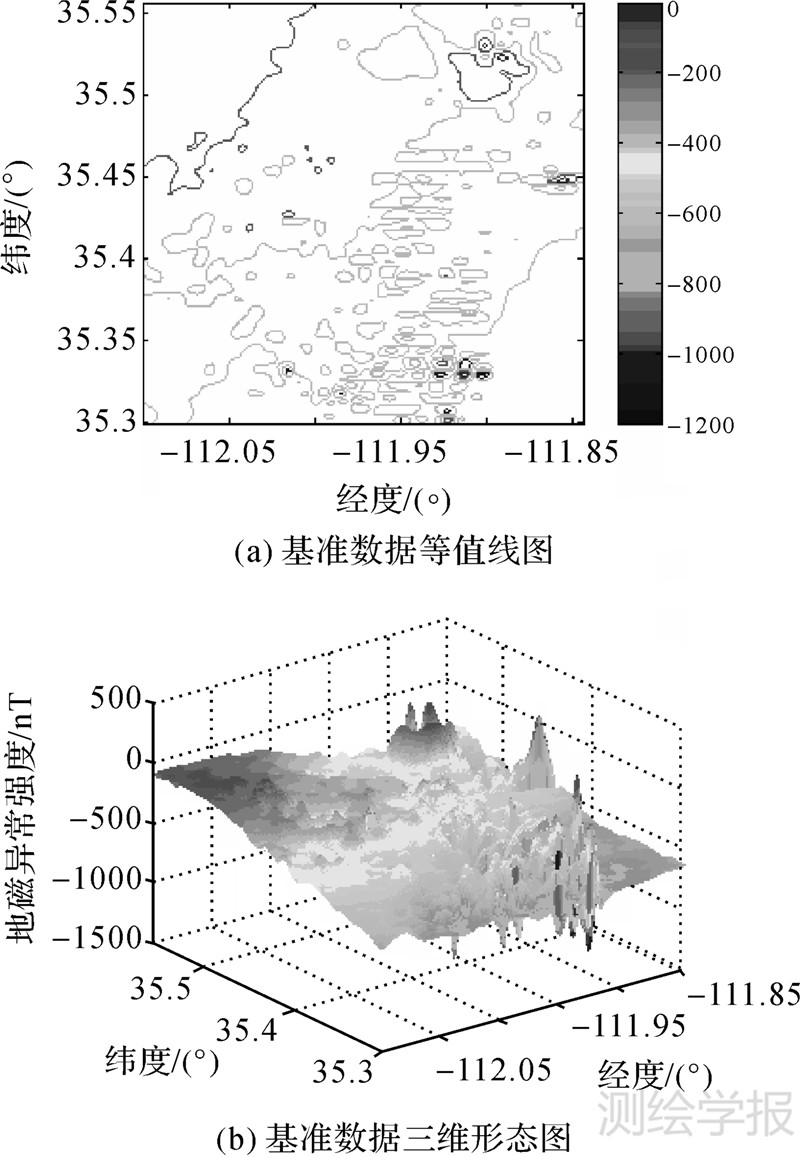
3 地磁异常场的多重分形谱分析本文研究的地磁异常场来自于NOAA发布的航磁测量数据,首先以编号为4109A的测量数据为例分析地磁异常场的多重分形特征。从中提取257×257个规则网格数据,网格分辨率为0.001°×0.001°,如图 1所示。
|
| 图 1 4109A地磁异常数据基准图 Fig. 1 The reference map of 4109A geomagnetic anomaly data |
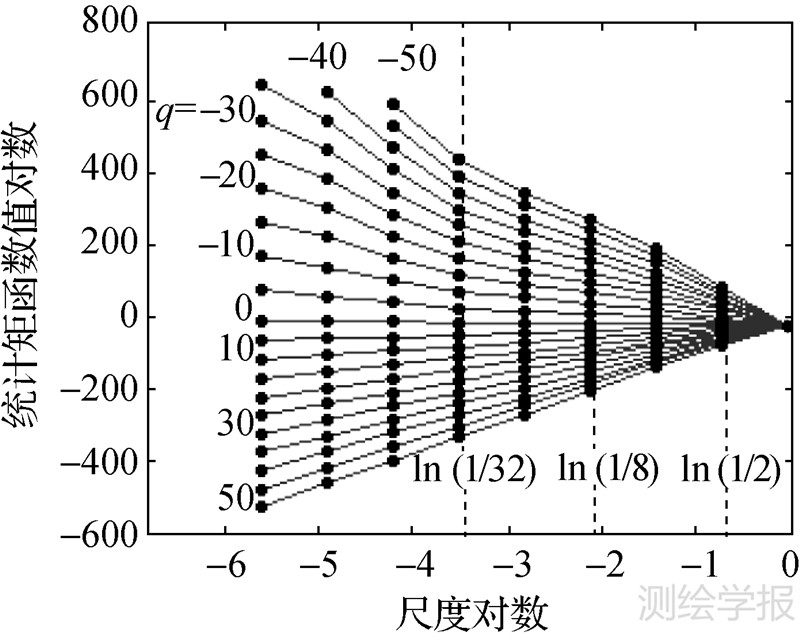
分别取盒子的边长r为1、2、4、8、16、32、64、128、256倍的单元网格边长,令研究区域的总边长为1,则对应的小盒子的边长分别为1/r。用以上边长的盒子覆盖数据集,根据式(8)计算每个盒子的概率,进而由式(5)可求得不同尺度的盒子覆盖数据集时的统计矩函数值,设定q的取值范围为[-50,50],绘制部分q值对应的ln χq(r)-ln r曲线如图 2所示。
|
| 图 2 ln χq(r)-ln r曲线 Fig. 2 Curves vary from ln χq(r)-ln r |
当q>0时,ln χq(r)和ln r呈现较强的线性特征,说明所研究数据集中的普通子集和大概率子集在全尺度范围内具有良好的标度不变性;q <0时,ln χq(r)和ln r线性特征依然明显,但在尺度为1/32处出现一定的转折,在[1/32,1]和[1/256,1/32]尺度范围内(即图中虚线两侧),ln χq(r)与ln r均具有良好的线性关系,这是因为尺度的减小凸显了局部区域小概率子集的特征,大尺度范围的标度不变性体现的是地磁异常场作为一种复杂空间变量在整体上的自相似特征,而小尺度范围内的分形特征需要在局部区域内进行分析。
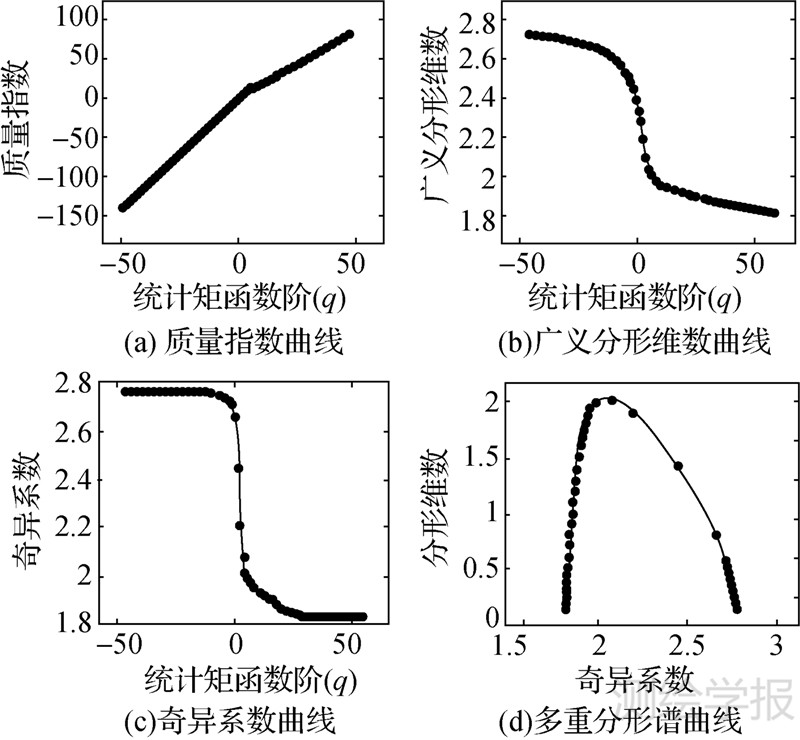
在[1/32,1]尺度范围内,绘制τ(q)-q曲线如图 3(a),曲线呈上凸形态,说明数据集具备多重分形特征。进一步求取不同q值对应的广义分形维数D(q)、奇异系数α(q),以及分形维数f(α),并绘制D(q)-q、α(q)-q以及多重分形谱f(α)-α曲线分别如图 3(b)、(c)、(d)所示。
|
| 图 3 多重分形谱分析图 Fig. 3 Multifractal spectrum analysis figure |
同样对4109B、 5041、5042、4052区域地磁异常数据进行分析,q取值范围及分析结果如表 1所示。当q在不同取值时,计算ln χq(r)、ln r在不同尺度范围内的相关系数,如表 2所示。
| 数据编号 | q值取值范围 | 最小奇异系数 | 最大奇异系数 | 标度不变性尺度范围 | 谱宽度 | 最大分维 | 最小分维 |
| 4109A | [-50,50] | 1.807 5 | 2.750 7 | [1/32,1] | 0.943 2 | 2 | 0.061 0 |
| 4109B | [-35,35] | 1.858 6 | 2.605 7 | [1/32,1] | 0.747 1 | 2 | 0.021 5 |
| 5041 | [-40,40] | 1.824 1 | 2.623 8 | [1/128,1] | 0.799 7 | 2 | 0.023 4 |
| 5042 | [-50,50] | 1.899 5 | 2.184 7 | [1/256,1] | 0.285 2 | 2 | 0.409 2 |
| 4052 | [-50,50] | 1.820 1 | 2.866 7 | [1/32,1] | 1.046 6 | 2 | 0.047 0 |
| 数据编号 | 拟合斜率转折点 | 大尺度范围线性相关系数 | 小尺度范围线性相关系数 | |||||||||
| 10 | -5 | -15 | -25 | -35 | 10 | -5 | -15 | -25 | -35 | |||
| 4109A | 1/32 | 0.999 7 | 0.998 5 | 0.997 9 | 0.997 8 | 0.997 7 | 1.000 0 | 0.998 6 | 0.998 4 | 0.998 4 | 0.998 4 | |
| 4109B | 1/32 | 0.999 7 | 0.999 5 | 0.997 7 | 0.997 0 | 0.996 8 | 1.000 0 | 0.997 5 | 0.995 5 | 0.995 4 | 0.995 3 | |
| 5041 | 1/128 | 1.000 0 | 0.999 9 | 0.999 1 | 0.999 0 | 0.998 9 | - | - | - | - | - | |
| 5042 | - | 1.000 0 | 1.000 0 | 0.999 9 | 0.999 8 | 0.999 7 | - | - | - | - | - | |
| 4052 | 1/32 | 1.000 0 | 0.996 5 | 0.994 3 | 0.994 0 | 0.993 9 | 1.000 0 | 0.988 5 | 0.987 8 | 0.987 8 | 0.987 8 | |
| 注:表中“-”表示该项不存在或无意义。 | ||||||||||||
表 1中,谱宽度由最大和最小奇异系数计算确定。谱宽度越大,说明相应数据集的分形子集奇异性越强;越小则说明数据集在整体上分布均匀,奇异性较弱。最大分维都为2,是因为所研究的数据集分布完全均匀,即在分析过程中,每个盒子均有概率分布;最小分维一般由奇异性较强的分形子集确定,分维越小,表明相应分形子集往往呈局域性分布且不均匀。
表 2中,拟合斜率转折点同表 1中标度不变性尺度范围相对应,对于大部分地磁异常数据集,ln χq(r)、ln r的拟合斜率具有比较明显的转折点,且在转折点前后均保持较强的线性关系,说明地磁异常数据集在局部上同样具有明显的分形特征。
在4109A数据集中选择5块尺度为1/32(即8个单元网格边长)的正方形区域,在每块区域中建立尺度1/32、1/64、1/128、1/256且平行嵌套的正方形簇,根据式(9)计算正方形内测度
式中,Ml为尺度l的正方形内的测度;Ni为正方形内的数据点个数;hj是第j个数据点的属性值。每个正方形的测度、尺度满足式(10)
式中,b为常数,α为该邻域内的奇异系数。计算5块区域中正方形簇的测度、尺度序列,并对其对数进行相关性分析,见表 3。可知,测度、尺度对数具备极强的线性相关性,说明地磁异常场在较小尺度的局部区域内具备明显的单一分形特征,线性拟合斜率即为相应区域的奇异指数。
| 区域编号 | 1 | 2 | 3 | 4 | 5 |
| 相关性 | 0.999 8 | 0.999 7 | 0.999 4 | 0.999 2 | 0.999 5 |
| 奇异系数 | 2.058 3 | 2.436 1 | 1.920 6 | 2.153 6 | 2.279 5 |
多重分形理论可以准确地描述地磁异常场在小尺度范围内的奇异性,而克里金法在低频段可以对未知点属性值进行准确地估计。本文提出逐步插值校正法,将多重分形理论和克里金法相结合,对未知位置进行插值和校正,逐步进行基准图的构建。
考虑到利用本方法在实际构图应用时,研究区域地磁异常场分形特征的不确定性,试验过程要遵循以下原则:
(1) 所选尺度范围不宜过大,一般取3~4个尺度量级,尽量保证尺度范围内ln χq(r)、lnr良好的线性特征。
(2) 若待校正位置邻域内的测度、尺度对数序列相关性在某点处出现明显转折,则将该点对应尺度作为线性拟合尺度范围上限。
(3) 采用克里金法估计未知点属性值时,搜索半径不超过插值参考数据最小间距的4~5倍。
以编号4109A的257×257标准网格数据作为基准,分别从中提取33×33和65×65网格数据作为构图参考数据,采用逐步插值校正法对基准数据进行重构,具体如下。
4.1 构图数据的分形特征分析利用多重分形理论对数据点进行奇异性校正,要求数据集必须满足多重分形特征。对33×33和65×65网格数据进行多重分形谱分析,绘制ln χq(r)-ln r线,如图 4所示。

|
| 图 4 构图数据ln χq(r)-ln r曲线图 Fig. 4ln χq(r)-ln r curve of reference data |
选取33×33数据中部分区域如图 5中符号“*”所示,具体步骤如下。
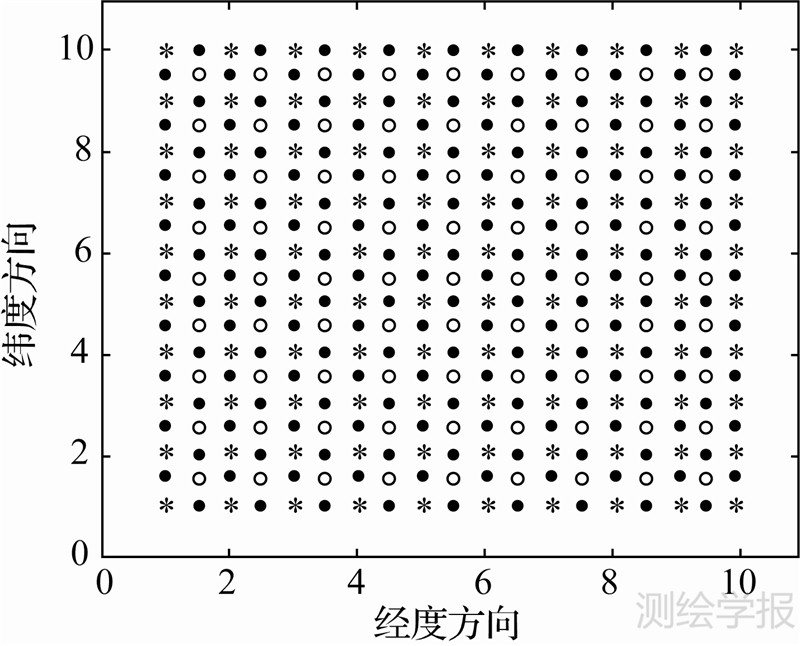
|
| 图 5 试验过程数据分布示意图(“*”为原始参考数据,“o”和“·”分别为参考数据的网格中心和网格边界中心) Fig. 5 Data distribution sketch map in experimental process |
步骤1:求取“o”位置的奇异系数。设构图参考数据网格边长为L,则以某一“o”点为中心,建立边长分别为L/2、L、3L、5L、7L且互相平行的正方形簇,利用式(9)计算后四者内的测度,根据式(10)和原则(2),对这4个正方形的测度、尺度对数进行线性拟合,拟合斜率即为待求α,该α满足边长L/2正方形的测度-尺度关系。
步骤2:对“o”位置进行插值并校正。对 “o”位置进行克里金插值估计,设结果为Z0,将插值参考区域转化为等面积、边长为k·(L/2)的正方形,Z0为该正方形内平均测度。将该位置真实值Z′作为边长L/2正方形内平均测度。上述两个正方形同时满足式(10)的测度、尺度关系,推算可得
此式即为对插值结果的奇异性修正方法。
步骤3:通过步骤1、步骤2可首先完成对图 5中所有“o”位置的插值和校正。进一步,按相同方法对所有 “·”位置进行相同操作,从而可得65×65的准确网格数据。
步骤4:在此基础上,重复两次步骤1-4的试验过程,得到和原始数据相同分布的257×257数据集,即完成了对基准数据集的重构。
同样,将从基准数据中提取的65×65网格数据作为构图参考数据,并进行重构试验。此外,试验过程中,采用镜像对称补偿方法对边界进行补偿,降低边界效应对构图结果的影响。
4.3 构图结果评价与分析 4.3.1 构图结果评价将33×33和65×65网格数据作为参考数据或训练样本,分别使用克里金法、改进谢别德法、BP神经网络法对257×257数据进行插值或预测重构,将重构结果和基准数据集以及4.2中分别以33×33和65×65网格数据为基础重构的数据集在同一剖线上进行对比,分别如图 6(a)、图 6(b)所示。

|
| 图 6 不同数据集剖线对比图 Fig. 6 Curves comparison of different datasets |
从两方面对构图结果进行评价:
(1) 通过图 6(a)、图 6(b)可以看出,相比单纯使用克里金法,本文方法能够更好地逼近基准数据,尤其在奇异性较强的局部细节上,这种优势尤其明显;相比改进谢别德法、BP神经网络法这些优异的传统插值方法或预测算法同样有着明显的优势,以上各方法的重构精度对比见表 4。
(2) 通过图 6和表 4可以看出,由65×65网格数据重构的数据集相比33×33网格数据在精度上有明显提升,在细节上可以更好地逼近真实数据特征。观察图 4(b)可知,ln χq(r)、ln r拟合斜率在尺度1/32处有一定的转折,说明65×65数据集中包含了更多的局部细节信息,尤其是强奇异性子集信息,它不仅使克里金法的估计更准确,同时可以更精确地描述每个位置的奇异特征。
| 区域编号 | 构图方法 | 基于33×33网格数据 | 基于65×65网格数据 | |||||
| 平均绝对残差/nT | 均方根预测误差/nT | 相对均方差 | 平均绝对残差/nT | 均方根预测误差/nT | 相对均方差 | |||
| 4109A | 本文方法 | 12.152 87 | 27.257 63 | 0.008 532 | 5.753 624 | 15.342 86 | 0.002 835 | |
| 克里金法 | 24.411 19 | 54.454 85 | 0.022 658 | 8.937 625 | 24.089 45 | 0.004 434 | ||
| 改进谢别德法 | 26.873 35 | 58.659 42 | 0.024 828 | 8.819 712 | 25.286 66 | 0.004 843 | ||
| BP神经网络法 | 51.811 22 | 78.073 73 | 0.046 575 | 50.356 94 | 77.048 73 | 0.045 361 | ||
| 4109B | 本文方法 | 12.265 34 | 32.324 95 | 0.0120 37 | 6.869 527 | 23.314 87 | 0.004 976 | |
| 克里金法 | 24.529 22 | 64.599 54 | 0.021 177 | 10.648 17 | 37.818 84 | 0.007 258 | ||
| 改进谢别德法 | 27.354 90 | 69.502 21 | 0.023 112 | 11.192 77 | 39.531 13 | 0.007 748 | ||
| BP神经网络法 | 79.740 08 | 110.350 5 | 0.061 794 | 81.881 77 | 111.434 26 | 0.063 013 | ||
| 5041 | 本文方法 | 6.321 687 | 10.986 54 | 0.003 345 | 3.036 581 | 5.864 826 | 0.000 639 | |
| 克里金法 | 12.537 42 | 21.498 14 | 0.006 593 | 4.685 087 | 9.022 953 | 0.001 161 | ||
| 改进谢别德法 | 12.732 59 | 22.548 26 | 0.006 845 | 4.725 169 | 9.106 842 | 0.001 203 | ||
| BP神经网络法 | 40.156 65 | 54.320 24 | 0.042 091 | 40.236 46 | 55.512 46 | 0.043 959 | ||
| 5042 | 本文方法 | 3.924 579 | 6.215 372 | 0.001 548 | 2.116 539 | 3.652 492 | 0.000 473 | |
| 克里金法 | 7.752 669 | 12.321 40 | 0.003 944 | 3.104 587 | 5.275 928 | 0.000 723 | ||
| 改进谢别德法 | 7.987 904 | 13.187 06 | 0.004 258 | 3.389 562 | 5.563 325 | 0.000 756 | ||
| BP神经网络法 | 23.499 88 | 31.614 67 | 0.025 963 | 25.516 88 | 34.302 73 | 0.030 567 | ||
| 4052 | 本文方法 | 5.912 857 | 12.586 31 | 0.001 587 | 2.153 876 | 5.632 574 | 0.000 287 | |
| 克里金法 | 11.994 96 | 25.077 06 | 0.004 474 | 3.212 158 | 8.186 948 | 0.000 477 | ||
| 改进谢别德法 | 12.420 55 | 26.140 71 | 0.004 644 | 3.346 748 | 8.303 975 | 0.000 491 | ||
| BP神经网络法 | 69.785 02 | 109.932 6 | 0.085 985 | 69.027 31 | 105.812 24 | 0.079 660 5 | ||
本文方法可以有效地提高克里金法构建地磁基准图的精度,并且相比其他传统方法具有明显的优势,但仍有一定的误差,主要原因有以下3点:
(1) 克里金法的估计误差。克里金法作为本文方法的基础组成部分,使用范围较广,且能比较有效地降低估计误差,但无法完全消除,同时有着低通滤波性等缺点。
(2) 边界效应的影响。一是在对边界附近位置进行克里金插值时,搜索区域会延伸到研究区域之外,导致参考点缺失现象;二是以边界附近位置点为中心建立正方形簇时,正方形同样会延伸到研究区域之外,从而对正方形的测度估计带来误差,虽然采用镜像对称补偿方法进行了边界补偿,并将这种误差降低了20%~40%,但很难完全消除。
(3) 强奇异性分形子集的丢失。当构图数据过于稀疏时,极有可能导致一些奇异性较强且分布比较集中的分形子集的丢失,体现在多重分形谱上就是谱宽度的降低。以试验分析的4109A数据为例,基准数据集谱宽度为0.943 2,而从中提取的33×33和65×65网格数据的分形谱宽度分别为0.382 5和0.578 4,从而对于基准数据集中某些奇异性较强的分形子集,无法做到完全的奇异性校正。当构图数据的分辨率大于0.01°时,本文方法的优势将很难得到体现,但是由于实测数据均在本文方法适用范围之内,因此本文方法具有良好的实用价值。
显然,本文方法的优越性主要体现在地磁异常变化比较明显,即适合进行地磁匹配的研究区域,在地磁异常变化平缓区域,意义比较有限。此外,相比传统方法,本文方法带来了更多的计算量,相比于单纯使用克里金法,计算量增加了一倍。
5 结 论地磁异常场的分布受不同区域地质结构的差异性及人为因素的影响,不仅水平梯度变化大,而且这种梯度变化很不一致。通过对5块区域的航磁测量数据进行多重分形特征分析,在不同尺度范围内对其标度不变性进行了定量地阐释。在大尺度范围内体现的是地磁异常场作为复杂空间变量的整体分布特征,而在小尺度范围内体现的是地磁异常场在局部范围内的简单分形特征,通过在特定范围内进行分析,可以很好地刻画地磁异常场的局部奇异性。
在分析地磁异常场多重分形特征的基础上,将多重分形理论和克里金法相结合,提出逐步插值校正法。试验证明相比克里金法、改进谢别德法等优异的传统插值或预测方法,本文方法能够更精确地进行基准图的构建,尤其在对局部奇异特征的刻画上,具有很强的优越性,当参考数据中包含细节信息较丰富时,可以最大程度地保证奇异性校正的充分性和准确性。经匹配仿真研究证明,采用本文方法构建的基准图,可以将地磁匹配的精度提高10%~20%,且对于大多数地磁异常场,可稳定在百米之内。本文方法可以很好地应用于地磁测量数据不严格均匀分布的情况,有效提高对局部奇异性的刻画,作为地磁测量的完好补充,为实现精确的地磁导航提供支撑。
| [1] | RICE H, KELMENSON S, MENDELSONHN L.Geophysical Navigation Technologies and Applications[C]// Position Location and Navigation Symposium,IEEE PLANS, 2004:618-624. |
| [2] | THIENEL J K, HARMA R R.Results of the Magnetometer Navigation(MAGNAV) in Flight Experiment[C]// AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, Rhode Island, 2004:1164-1182. |
| [3] | KOU Yimin. Research of Key Technologies in Geomagnetic Navigation[D]. Harbin:Harbin Institute of Technology, 2010.(寇义民. 地磁导航关键技术研究[D]. 哈尔滨:哈尔滨工业大学,2010.) |
| [4] | QIAO Yukun, WANG Shicheng, ZHANG Jinsheng, et al. BP Neural Network Based Preparation Method of Geomagnetic Reference Map and Its Accuracy Evaluation[J]. Journal of Chinese Inertial Technology, 2009,17(1):53-58.(乔玉坤,王仕成,张金生,等. 基于BP网络的地磁基准图制备及其精度评价[J]. 中国惯性技术学报,2009,17(1):53-58.) |
| [5] | ZHANG Xiaoming, ZHAO Yan. Local Geomagnetic Field Mapping Based on Kriging Interpolation Method[J]. Electronic Measurement Technology, 2009, 32(4):122-125.(张晓明,赵剡. 基于克里金法的局部地磁图的构建[J]. 电子测量技术,2009,32(4):122-125.) |
| [6] | YANG Gongliu, ZHANG Guimin, LI Shixin. Application of Universal Kriging Interpolation in Geomagnetic Map[J]. Journal of Chinese Inertial Technology, 2008,16(2):162-166.(杨功流,张桂敏,李士心. 泛克里金插值法在地磁图中的应用[J]. 中国惯性技术学报,2008,16(2):162-166.) |
| [7] | WANG Huizan, ZHANG Ren, LIU Wei, et al. Kriging Interpolation Method Optimized by Support Vector Machine and Its Application in Oceanic Data[J].Transactions of Atmospheric Sciences, 2011,34(5):567-573.(王辉赞,张韧,刘巍,等. 支持向量机优化的克里金插值算法及其海洋资料对比试验[J]. 大气科学学报,2011,34(5):567-573.) |
| [8] | MANDELBROT B B. How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension[J]. Science, 1967, 156:636-638. |
| [9] | SUN Xia, WU Ziqin, HUANG Yun. Principles and Application of Fractal[M]. Hefei:University of Science and Technology of China Press,2003.(孙霞,吴自勤,黄畇. 分形原理及其应用[M]. 合肥:中国科学技术大学出版社,2003.) |
| [10] | SPECTOR A, GRANT F S. Statistical Models for Interpreting Aeromagnetic Data[J]. Geophysics, 1970,35(2):293-302. |
| [11] | MARK E G, OLIVIA J, JAFAR A H. Fractal Stochastic Modeling of Aeromagnetic Data[J]. Geophysics, 1991, 56(11):1706-1715. |
| [12] | JIANG Xiaodian, YU Zenghui. Study on the Fractal Character of Magnetic Anomaly Fields and the Delineation of Tectonic Elements in the South China Sea[J]. Chinese Journal of Oceanology and Limnology, 1998, 16(1):28-35. |
| [13] | WU Zhaocong. Determination of Fractal Scaleless Range[J]. Acta Geodaetica et Cartographica Sinica, 2002,31(3):240-244.(巫兆聪. 分形分析中的无标度区确定问题[J]. 测绘学报, 2002,31(3):240-244.) |
| [14] | SUN Xia, WU Ziqin. Fractal and Multifractal Description of Surface Topography [J]. Acta Physica Sinica, 2011, 50(11):2126-2131.(孙霞,吴自勤. 规则表面形貌的分形和多重分形描述[J]. 物理学报,2011,50(11):2126-2131.) |
| [15] | QIAN Dong, LIU Fanming, LI Yan, et al. Comparison of Gravity Gradient Reference Map Composition for Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6):736-744.(钱东,刘繁明,李艳,等.导航用重力梯度基准图构建方法的比较研究[J]. 测绘学报, 2011,40(6):736-744.) |
| [16] | ARIZA-VILLAVERDE A B, JIMENEZ-HORNERO F J, EDUARDO G D R. Multifractal Analysis of Axial Maps Applied to the Study of Urban Morphology[J]. Computers, Environment and Urban Systems, 2013, 38:1-10. |
| [17] | LI Qiang, XU Guiming. Scale Invariance in Complex Seismic System and Its Uses in Gaining Precursory Information before Large Earthquakes: Importance of Methodology[J]. Physica A:Statistical Mechanics and Its Applications, 2013, 392(4):929-940. |
| [18] | XU Guoce, LI Zhanbin, LI Peng. Fractal Features of Soil Particle-size Distribution and Total Soil Nitrogen Distribution in a Typical Watershed in the Source Area of the Middle Dan River, China[J]. Catena, 2013, 101:17-23. |
| [19] | LI Tong, SHANG Pengjian. A Multifractal Approach to Palmprint Recognition[J]. Acta Physica Sinica, 2007, 56(8):4393-4400.(李彤,商朋见. 多重分形在掌纹识别中的研究[J]. 物理学报,2007,56(8):4393-4400.) |
| [20] | JIANG Zhiqiang. Some Questions in the Applications Research of Fractal and Analyse of Its Present Situation and Foreground[J]. Journal of Jilin University, Information Science Edition,2004, 22(1):57-62.(姜志强. 分形理论应用研究若干问题及现状与前景分析[J]. 吉林大学学报:信息科学版, 2004,22(1):57-62.) |
| [21] | YANG Juan, BIAN Baomin, YAN Zhengang, et al. Fractal Characteristics of Characteristic Parameter Statistical Distributions of Typical Random Signals[J]. Acta Physica Sinica, 2011, 60(10):86-92.(杨娟,卞保民,闫振纲,等. 典型随机信号特征参数统计分布的分形特性[J]. 物理学报,2011, 60(10):86-92.) |
| [22] | SUN Xia, XIONG Gang, FU Zhuxi, et al. Multifractal Spectra of Atomic Force Microscope Images of ZnO Film[J]. Acta Physica Sinica, 2000, 49(5):854-862.(孙霞,熊刚,傅竹西,等.ZnO薄膜原子力显微镜图像的多重分形谱[J]. 物理学报. 2000,49(5):854-862.) |
| [23] | YANG Xiaodong, NING Xinbao, HE Aijun, et al. Mass Exponent Spectrum Analysis of Human ECG Signals Based on Multiple Scale Factors[J]. Acta Physica Sinica, 2008, 57(3):1514-1521.(杨小冬,宁新宝,何爱军,等. 基于多尺度的人体ECG信号质量指数谱分析[J]. 物理学报, 2008,57(3):1514-1521.) |