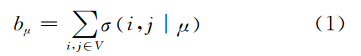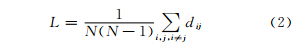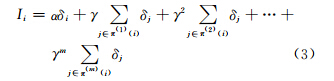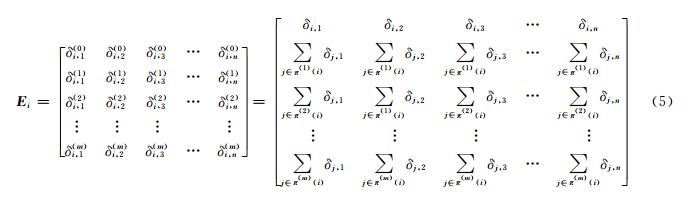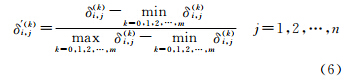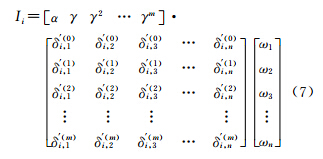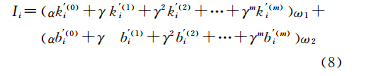1 引 言
道路选取是地图综合中的重要操作之一,指在比例尺缩小后将数据中不符合目标尺度要求的冗余目标舍弃,筛选出重要道路构成路网并保持所选路网的拓扑连通性[1, 2, 3]。道路选取的主要困难在于所选路网应保持原始路网的整体结构和局部关键结构[4]。目前,选取方法的研究主要集中在两个方面:基于路网线状表示的方法[5, 6, 7, 8]和基于路网构面表示的方法[3, 9, 10]。这些方法从不同的角度选取道路,例如考虑道路的几何、拓扑、等级等属性[11, 12]。在众多属性中,连通关系和几何特征是道路最基本、最重要的属性,它们是构成路网整体形态及影响路网功能的关键因素。因而,采用道路几何与连通关系进行道路选取其方法的实用性较高[8]。
文献[2]基于图论提出一种结构化道路选取方法,指出通过路段重要性评价来提取道路,拓展了道路选择的研究思路。然而,由于其方法独立地使用连接中心度和邻近中心度进行道路提取,很难得出一致的选取结果。文献[7]提到“路段”和“路径”的重要区别,引入路划的概念进而提出一种基于路划的道路选取方法。该方法不直接对单个路段作选取,而是从道路自然延伸形态的角度通过采用感知分组原理构造更大的选取单元,即路划,且道路选取的衡量标准为路划长度。该方法有效地顾及了道路的几何属性,但忽略了路网的拓扑特性,仅依靠路划长度进行道路选取较难保持原始路网的整体结构及连通关系。
在文献[2, 7]的基础上,文献[8]考虑道路几何结构和连通关系,提出以路划为选取单元、以路划网络功能为选取指标的道路选取方法,认为道路的重要性体现在道路在路网中的功能,并将此功能定义为道路在全局意义上提供跨越空间的通路和在局部意义上提供连接空间的通路,其道路选取结果优于文献[7]。然而,该方法将路划作为单个对象处理,没有考虑路划之间的相互作用,可能导致路划网络功能评价缺乏准确性和可靠性。此外,如果两相邻路段属性(如等级)存在较大差异,很难保证采用感知分组原理所构造的路划的合理性。
总体而言,目前道路选取方法大多还是基于图论和GIS网络分析理论。采用图论和GIS网络分析方法对于研究路网的结构特征具有一定的积极作用,但不能很好地描述路网结构的整体形态及复杂性[13]。为此,本文试图采用基于对偶拓扑方法的复杂网络理论来研究道路的选取问题。通过引入m阶邻居节点的概念,将对偶图中节点的重要度定义为节点自身及1到m阶邻居节点重要度贡献的总和,并以节点度、介中心及节点间距离为度量参数建立节点重要度评价模型,进而提出一种基于对偶图节点重要度评价的道路选取方法。
2 网络拓扑图的建立及拓扑结构特征指标
2.1 道路网络的对偶拓扑表达
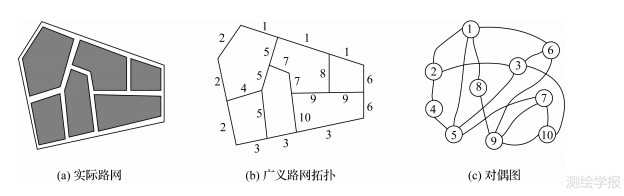
在GIS领域,最常用的网络拓扑方法是直接对实际路网做抽象,即以道路为边、交叉口为节点建立广义路网拓扑[14]。近年来,复杂网络理论逐渐运用到交通、GIS领域,有助于深入分析路网结构的复杂性及功能特性。利用对偶拓扑方法将道路按路名映射为节点、交叉口映射为边可以建立基于广义路网拓扑的对偶图。如图 1所示,图 1(a)为实际路网,图 1(b)为广义路网拓扑,图 1(c)为基于广义路网拓扑的对偶图。较广义路网拓扑,采用对偶拓扑能更加深入地分析路网结构及其对路网功能的影响,可以进一步分析道路之间的连接关系、线路的交通特性、路网的连通性、可靠性以及道路在整个路网中的重要程度。
|
| 图 1 交通网络拓扑结构 Fig. 1 Transportation network topology structure |
2.2 网络拓扑结构特征指标
设G=V,L是基于广义路网拓扑建立的对偶图,其中V是网络中所有节点的集合且节点数量为N,L为网络中所有边的集合。
2.2.1 节点度
节点度是指网络拓扑中与此节点直接相连的边的数量,记为k,它是研究网络拓扑结构的基本参数。目前普遍认为节点度可以直接反映节点的重要性,度越高,则该节点越重要。
2.2.2节点介中心
节点介中心是度量网络节点重要性的方法,给出在网络中一个节点处通过的最短路径的情况,反映了节点在网络路径选择中的重要程度[15]。理论上两节点之间最短路径只有一条,特别是针对道路网络而言,两点间很少有两条以上的最短路径。故这里设Pi,j为节点i与j之间的唯一最短路径,用σi,j|μ表示以i、j为起讫节点且通过节点μ的最短路径数量,如果μ在路径Pi,j上,那么σi,j|μ=1;否则,σ(i,j|μ)=0。这样,μ的介中心定义为
式中,i∈V,j∈V且i≠j,通过提取所有节点对间的最短路径,便可计算每个节点的介中心。
2.2.3 节点距离
节点距离是指两个节点之间最短路径上的边数,用d表示。如果节点i和j之间不存在路径,则dij→∞。网络中任意两个节点之间距离的最大值为网络的直径D,任意两个节点之间距离的平均值为网络的平均路径长度L
3 对偶图节点重要度评价方法
3.1 m阶邻居节点
在已有研究中,通常将与某节点直接相连的节点称作该节点的邻居节点。一定程度上,节点的重要性受其邻居节点的影响,但不是只有相邻节点才会影响其重要性。为此,这里对邻居节点的概念作如下扩展:对于网络G=V,L中节点i(i∈V),将与i距离为1的节点称做i的1阶邻居节点,该类节点构成的集合称做i的1阶邻居节点集,记为π(1)(i);同理,与i距离为2的节点为2阶邻居节点,其构成的集合称做i的2阶邻居节点集,记为π(2)(i);如此类推,则与i距离为m的节点称为i的m阶邻居节点,其构成的集合为i的m阶邻居节点集,记为π(m)(i)。图 2所示,节点i的1阶邻居节点集为{a,b,c,d,e,f,g},2阶邻居节点集为{h,j,v}。由于网络上没有节点存在D+1阶邻居节点,故m的取值应满足D≥m≥0。
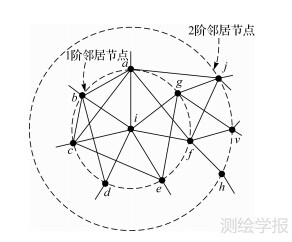
|
| 图 2 邻居节点示意图 Fig. 2 Sketch map of neighbors |
3.2 节点重要度评估策略
评估节点重要性的方法有很多,且本质上都是源于图论和基于图的数据挖掘[16, 17, 18]。笔者认为,节点重要性并不完全由节点自身属性所决定,在一定程度上还受到相邻节点及距离更远节点的影响,故节点重要性是节点自身及多阶邻居节点共同作用的结果。从空间自相关的角度,两个对象距离越近,则对彼此的依赖越强。由此,距离当前节点越近的节点,其对该节点重要性的贡献越大。研究表明,很多复杂系统的某些特性随距离增加都表现出指数衰减趋势。这里,不妨假设邻居节点的重要度贡献随距离的增加呈指数衰减形式。
为此,引入α和γ两个参数,分别用于调节节点重要性对节点自身及1到m阶邻居节点的依赖程度。从空间自相关的角度,为充分考虑节点自身及邻居节点的重要度贡献,定义α和γ的取值满足kγ>α>γ且1>γ>0,其中k为节点的平均度。当只考虑节点单一特性对其重要性的影响时,针对节点i,定义如下节点重要度评价函数
式中,Ii为节点i的重要性指标;δ为节点的属性值,如节点度、介中心等。由公式(3)可知,该评价函数综合考虑了节点自身及1到m阶邻居节点的重要度贡献,且距离i越远,其对i的重要度贡献越小。为便于理解,这里不妨将m称做节点重要度评估所考察的邻居节点深度。
对于网络节点而言,其重要性并不完全取决于节点的度、介中心或其他特性,需要同时顾及这些因素,才能对节点的重要性作出较为准确的评估。假设选取n个评价指标,δi,j为节点i的第j个指标值。由此,可以定义节点i的重要度评价模型
式中,Ii为节点i的重要度;A为评估系数矩阵或重要度贡献矩阵,表示节点自身及各阶邻居节点对其重要性的贡献程度,认为同阶邻居节点具有相等的贡献程度,即评估系数相等;Ei为i的评估指标矩阵,包含i及各阶邻居节点的指标值;W为指标权重矩阵,表示i的重要性对各类指标的依赖程度,这里将n个指标所占权重分别记为ω1ω2…ωn。设节点i的n个指标值分别为δi,1,δi,2,δi,3,…,δi,n,故公式(4)中Ei可表示为
式中,δ(m)i,n表示i的m阶邻居节点集的第n个指标的重要度贡献;δj,n(j∈π(m)(i))为i的m阶邻居节点集中节点j的第n个指标值。由于各指标的物理意义和计量单位不一定相同,导致数据的量纲和数量级可能不同,故须对Ei作归一化处理
式中,δ′(k)i,j为归一化后的指标值,进而得到归一化评估指标矩阵E′i。令A=[αγγ2…γm],W=ω1ω2
式中,ω1ω2…ωn为各指标所占权重,满足∑nj=1ωj=1且ωj≥0,j。
3.3 道路网对偶图节点重要度评价
道路选取的基本原则是从大比例尺路网中按规则选择重要的道路。所以,如何评价道路的重要性是道路选取的关键。笔者认为,道路重要性评估需要考虑道路的拓扑属性及其对路网传输过程的影响。将对偶图节点按度进行排序,可以在一定程度上反映节点的重要性。节点度越高,则该节点越重要。但仅从节点度的大小并不能准确地表达节点在网络中的重要程度。除了度值,节点的重要性还跟其在网络中所处位置、与之相连的其他节点的重要性密切相关。中心性是度量网络节点重要性的主要方法,而节点介中心又是中心性度量的主要方法之一,它给出了在网络中一个节点处通过的最短路径,反映了节点连通能力的聚集度及对网络传输过程的影响程度[15, 19, 20]。为此,综合考虑度和介中心指标,顾及节点自身及1到m阶邻居节点的重要度贡献,基于公式(7)建立如下路网对偶图节点重要度评价模型
式中,k′(0)i、k′(1)i、…、k′(m)i为归一化的度值信息;b′(0)i、b′(1)i、…、b′(m)i为归一化的介中心值信息;ω1、ω2为度和介中心所占权重,用于调节节点重要性对度和介中心的依赖程度,且ω1+ω2=1。该模型考虑了节点的度、介中心及其与邻居节点的距离,随着邻居节点深度m的增加,m阶邻居节点的重要度贡献呈γm指数衰减。本文方法引入m阶邻居节点作为节点重要性的考察对象,顾及节点自身特性及1到m阶邻居节点的重要度贡献,相当于同时利用了节点的拓扑信息和位置信息,可较为准确地表达道路在整个路网中的重要性。
4 基于节点重要度评价的道路网自动选取方法4.1 道路网自动选取方法
基于节点重要度评价结果,可以依据对偶图中节点的重要度由高到低选取一定数量的节点,由此构建所选取的对偶图,然后基于最小规模原则通过增加节点的方式保持该对偶图的连通性,最后根据道路与对偶图节点的映射关系得到所选取的道路网络。设原始对偶图规模为N,为获取不同比例尺下的路网结构,假设按一定比例选取该比例下最重要的道路,且选取比例为S。由此,可以定义制图综合后得到的对偶图的规模为
Ns=NS(9)
由此,可以提出一种基于路网对偶图节点重要度评价的道路选取方法,具体过程如下:(1) 构建路网的对偶图G=V,L,建立其节点与原始广义路网拓扑中道路间映射关系。
(2) 获取对偶图中任意节点i的1到m阶邻居节点集:π(1)(i)、π(2)(i)、…、π(m)(i)。
(3)计算节点i的1到m阶邻居节点集的度值k(0)i、k(1)i、k(2)i、…、k(m)i和介中心值b(0)i、b(1)i、b(2)i、…、b(m)i,然后作归一化处理得到k′(0)i、k′(1)i、k′(2)i、…、k′(m)i和b′(0)i、b′(1)i、b′(2)i、…、b′(m)i。
(4) 根据公式(8),计算每个节点的重要度Ii。
(5) 针对所有节点,按重要度从大到小进行排序,得到一组新的节点序列v1、v2、v3、…、vN。
(6) 根据预定选取比例S,从上述节点序列中提取最前面紧邻的NS个节点及这些节点之间的所有连边,构建选取比例S下的对偶图Gs=Vs,Ls。
(7) 对Gs=Vs,Ls进行连通性检查,按4.3中的连通性保持算法确保Gs全域的连通性。
(8) 基于对偶图Gs=Vs,Ls,根据节点与道路间的映射关系从原始广义路网拓扑中提取Gs网络中所有节点相应的道路,进而构建选取比例S下的道路网络。
4.2 连通性保持算法
道路选取的基本要求是保持选取后路网的拓扑连通。根据对偶图的构建原则可知,保持广义路网拓扑的连通等价于保持对偶图的拓扑连通。由此,针对选取比例S下选取的对偶图Gs=Vs,Ls,本文通过增加最小数目的节点来连通所选网络。具体的连通性保持算法如下:
(1)提取对偶图Gs=Vs,Ls中的所有孤立节点,形成孤立节点集V′s。 (2)针对任意节点i(i∈V′s),计算距离i最近的某节点j(j∈Vs且jV′s),获取i与j之间的最短路径,将路径上所有节点v(vVs)添加到Gs,更新Vs、Ls,并从V′s中移除i。
(3)重复步骤(2),直到对偶图Gs=Vs,Ls中无孤立节点。
5 试验与讨论
根据成都市城区2007年交通图,按路名提取全部共1484条道路,构建原始广义路网拓扑,如图 3所示。基于该路网结构,采用对偶拓扑方法构建路网对偶图,包含1484个节点,5226条边,网络平均路径长度L=3.9130,节点平均度k=7.043 1,网络直径D=7。这里,认为度和介中心同等重要,即ω1=ω2=0.5。
为检验本文方法的有效性,针对原始路网在不同选取比例下进行道路选取试验。图 4给出了选取比例为0.01、0.05、0.10、0.20、0.30、0.40等6种取值下的道路选取结果,且m=4,α=1,γ=0.5。从图中可以看出:
此外,试验发现,无论选取比例为何值,选取的路网均能保持良好的拓扑连通,几乎无需用连通性保持算法进行连通性修复,这不仅确保了算法的运算效率,同时说明本文方法在路网选取初期便具备良好的连通保持特性。由此可知,本文方法具有较高的稳定性和可靠性。
由本文算法原理可知,邻居节点深度m的取值直接影响道路重要性评价结果,并最终影响道路的选取效果。若m取值太小,道路重要度评价主要依赖道路自身特性,可能导致评价结果不合理、不准确;若m取值太大,大量较远的邻居节点将参与重要度评价过程,增大算法的运算负荷,而且也有可能对道路重要度评价造成负面效果。为此,针对本文方法在m取值下进行了道路选取试验。由于m的取值只有在[0,D]范围内才有意义,所以,只需对0≤m≤7的值进行试验。结果发现,当m达到一定值后,所选取的道路将不再随m的持续增大而变化,道路选取过程表现出较强的可靠性和稳定性。
由本文方法原理可知,导致这种动力学现象的原因在于对偶图节点的重要度指标与m之间的约束关系。为此,给出了5条关键道路的重要度随m的变化情况,如图5所示。结果显示,当m较小时,节点的重要度I随m取值的增大变化较大,即I对m较为敏感; 当m大于对偶图的平均路径长度L时,节点的重要度I将不再随m的增加而变化,道路重要性评价进入稳定状态。由此,可以得出一个重要结论:只要m取值大于对偶图的平均路径长度L,本文方法便能得到稳定的道路重要性评价结果,保证道路选取的准确性和可靠性。
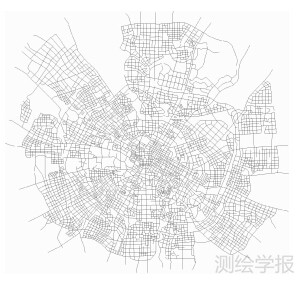
图 3 成都市城区广义路网结构
Fig. 3 Generalized road network of Chengdu city
①在各选取比例下,即便选取比例非常小,所选路网保持拓扑连通,较好地覆盖了原始路网的整体范围;
②在各选取比例下,所选路网保持了原始路网的整体结构;
③在各选取比例下,路网密度特征得以保持,原始路网中相对密集(或稀疏)的区域在所选路网中仍得以体现;
④随着选取比例的增大,所增选的道路较为合理,有效地顾及了原始路网的密度和整体结构,道路层次性得以体现。由此可知,本文道路选取方法较好地顾及了道路的拓扑和位置信息,能较好地满足道路网自动综合的基本要求。
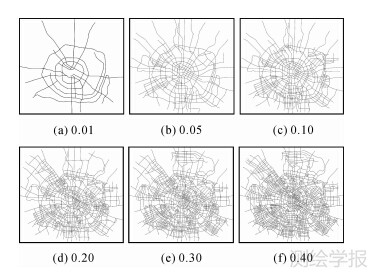
图 4 不同选取比例下道路选取结果
Fig. 4 Roads selection results at various selection ratios
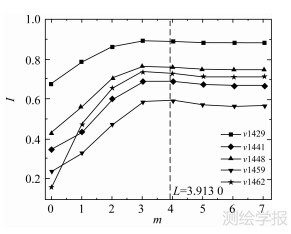
图 5 道路重要度指标I与m的关系
Fig. 5 The relation of I and m
根据图 5中所选道路,采用目视查看方法可以得出选取的道路网络保持了原始路网的整体结构及拓扑连通性。为进一步论证本文方法的有效性,需要采用定量评价的方法分析道路选取效果。已有研究表明,网络的度分布与其拓扑结构紧密相关,网络的拓扑结构性质及网络上的动力学行为等均紧密依赖于网络的度分布,而对于无标度网络而言,其度分布则完全由度分布指数所确定[21]。
为进一步分析所选取路网与原始路网的拓扑特性,研究所选路网对原始路网拓扑结构的保持程度,分别对原始对偶图及不同选取比例下提取的对偶图的度分布情况进行了统计分析,结果分别如图 6和图 7所示,且α=1,γ=0.5,ω1=ω2=0.5。统计结果显示:原始对偶图中节点的度分布服从幂律分布,说明该城市道路网络具有无标度特性;对于所选取的道路,无论选取比例为何值,道路网络的度分布均表现出无标度特性,同时发现其幂律指数均近似等于原始对偶图的幂律指数。由此表明,本文方法选取的路网没有改变原始路网的无标度特性,较好地保持了原始路网的整体拓扑结构。
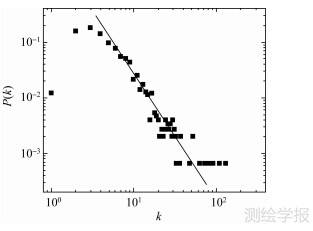
|
| 图 6原始道路网络的度分布 Fig. 6 The degree distribution of original road network |
6 结 论
道路的自动选取是道路网自动综合领域的关键问题,其主要困难在于选取的道路应保持原始路网的整体结构。认为道路选取的关键在于准确、合理地评价道路的重要性。为此,利用对偶拓扑方法构建基于广义路网拓扑的对偶图,顾及道路的位置及拓扑信息,定义针对该对偶图的节点重要度评价模型,据此提出以道路重要度为考察指标的道路选取方法。
以成都市城区路网为试验数据,针对不同选取比例和不同邻居节点深度进行道路选取试验。结果表明:本文方法选取的路网能较好地保持原始路网的整体结构、拓扑连通性、路网密度及覆盖范围,道路层次性得以体现;引入m阶邻居节点评价道路重要性是合理的,顾及节点自身及m阶邻居节点的重要度贡献有助于衡量道路在拓扑及几何位置方面的重要性;从路网的度分布可知,所选路网能较好地保持原始路网的拓扑特性,且不依赖于选取比例;本文方法以道路的几何、连通关系为考察数据,不依赖于道路属性数据,方法适用性较强;在保持路网整体结构、路网密度、拓扑特性及路网层次性等方面,本文方法优于单纯按路划长度以及按网络中心度选取的效果;同时,试验还揭示了一个重要的动力学现象,即当m大于对偶图的平均路径长度L时,道路重要度评价趋于稳定,得到的评价结果较为可靠,保证道路选取结果的有效性。
| [1] | MACKANESS W A. Analysis of Urban Road Networks to Support Cartographic Generalization[J]. Cartography and Geographic Information Systems, 1995, 22(4): 306-316. |
| [2] | JIANG B, CLARAMUNT C. A Structural Approach to the Model Generalization of an Urban Street Network[J]. GeoInformatica, 2004, 8(2): 157-171. |
| [3] | HU Yungang, CHEN Jun, LI Zhilin, et al. Selective Omission of Road Features Based on Mesh Density for Digital Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 351-357. (胡云岗, 陈军, 李志林, 等. 基于网眼密度的道路选取方法[J]. 测绘学报, 2007, 36(3): 351-357.). |
| [4] | CHEN Bo, WU Fang, QIANG Haizhong. A Study on Road Networks’ Auto-selection Algorithms[J]. Journal of Image and Graphics, 2008, 13(2): 2388-2393. (陈波, 武芳, 钱海忠. 道路网自动选取方法研究[J]. 中国图象图形学报, 2008, 13(2): 2388-2393.). |
| [5] | CHAUDHRY O, MACKANESS M. Rural and Urban Road Network Generalization: Deriving 1: 250, 000 from OS Master Map[C]//Proceedings of International Cartographic Conference. Coruna:[s. n.], 2005. |
| [6] | TOUYA G. A Road Network Selection Process Based on Data Enrichment and Structure Detection[J] .Transactions in GIS,2010, 14( 5): 595 - 614. |
| [7] | THOMSON R C, RICHARDSON D E. The Good Continuation Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]//Proceedings of 19th International Cartographic Conference. Ottawa: ICA, 1999: 1215-1223. |
| [8] | XU Zhu, LIU Caifeng, ZHANG Hong, et al. Road Selection Based on Evaluation of Stroke Network Functionality[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 769-776. (徐柱, 刘彩凤, 张红, 等. 基于路划网络功能评价的道路选取方法[J]. 测绘学报, 2012, 41(5): 769-776.). |
| [9] | WANNING P, MULLER J C. A Dynamic Decision Tree Structure Supporting Urban Road Network Automated[J]. The Cartographic Journal, 1996, 33(1): 5-10. |
| [10] | CHEN J, HU Y, LI Z L, et al. Selective Omission of Road Features Based on Mesh Density for Automatic Map Generalization[J]. International Journal of Geographical Information Science,2009, 23(8): 1013-1032. |
| [11] | ZHOU Q, LI Z. Evaluation of Properties to Determine the Importance of Individual Roads for Map Generalization[J]. Advances in Cartography and Giscience, 2011, 5(1): 459-475. |
| [12] | DENG Hongyan, WU Fang, WANG Huilian, et al. A Generalization of Road Networks Based on Topological Similarity[J]. Journal of Geomatics Science and Technology, 2008, 25(3): 183-187. (邓红艳, 武芳, 王辉连, 等. 基于拓扑相似性的道路网综合模型[J]. 测绘科学技术学报, 2008, 25(3): 183-187.). |
| [13] | DENG Yajuan, YANG Yunfeng, MA Rongguo. Highway Network Structure Characteristics Based on Complex Network Theory[J]. China Journal of Highway and Transport, 2010, 23(1): 98-104. (邓亚娟, 杨云峰, 马荣国. 基于复杂网络理论的公路网结构特征[J]. 中国公路学报, 2010, 23(1): 98-104.). |
| [14] | BARTHLEMY M. Spatial Networks[J]. Physics Reports, 2011(499): 1-101. |
| [15] | LI Qingquan, ZENG Zhe, YANG Bisheng, et al. Betweenness Centrality Analysis for Urban Road Networks[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 37-41. (李清泉, 曾喆, 杨必胜, 等. 城市道路网络的中介中心性分析[J], 武汉大学学报:信息科学版, 2010, 35(1): 37-41.). |
| [16] | WEST D B. Introduction to Graph Theory[M]. Upper Saddle River:Prentice Hall, 2001. |
| [17] | WASHIO T, MOTODA H. State of the Art of Graph-based Data Mining[J]. SIGKDD Explore News, 2003, 5(1):59-68. |
| [18] | HE Nan, LI Deyi, GAN Wenyan, et al. Mining Vital Nodes in Complex Networks[J]. Computer Science, 2007, 34(12): 1-5. (赫南, 李德毅, 淦文燕, 等. 复杂网络中重要性节点发掘综述[J]. 计算机科学, 2007, 34(12): 1-5.) .. |
| [19] | CRUCITTI P, LATORA V, PORTA S. Centrality in Networks of Urban Streets[J]. Chaos, 2006, 16(1): 15113-15122. |
| [20] | LIU Gang, LI Yongshu. Routing Strategy for Complex Networks Based on Gravitation Field Theory[J]. Acta Physica Sinica, 2012, 61(24): 248901. (刘刚, 李永树. 基于引力场理论的复杂网络路由选择策略研究[J]. .物理学报, 2012, 61(24): 248901.) . |
| [21] | WANG Lin, DAI Guanzhong. On Degree Distribution of Complex Network[J]. Journal of Northwestern Polytechnical University, 2006, 24(4): 405-409. (王林, 戴冠中. 复杂网络的度分布研究[J]. . 西北工业大学学报, 2006, 24(4): 405-409.) . |