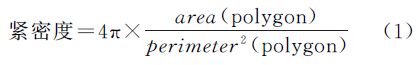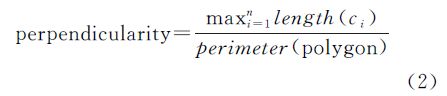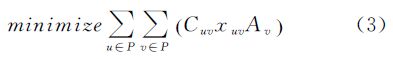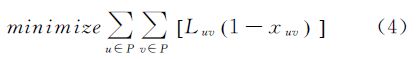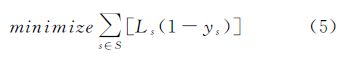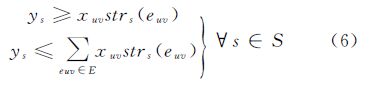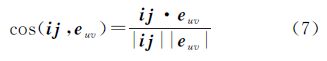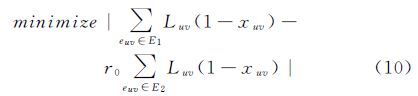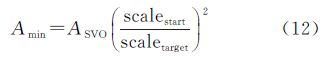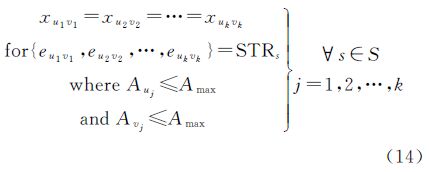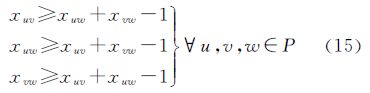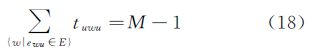2. 武汉大学 时空数据智能获取技术与应用教育部工程研究中心,湖北 武汉 430079;
3. 广东瑞图万方科技股份有限公司,广东 佛山 528305;
4. 中山大学 地理科学与规划学院综合地理信息研究中心,广东 广州 510275
2. Engineering Research Center for Spatio-temporal Data Smart Acquisition and Application, Wuhan University, Wuhan 430079, China;
3. Guangdong Ritu Information Systems Co Ltd, Foshan 528305, China;
4. Center of Integrated Geographic Information Analysis, School of Geography and Planning, Sun Yat-sen University, Guangzhou 510275 , China
道路选取对于路网制图综合、多尺度表达,以及道路等级分析都具有重要意义。被选取的道路不仅应反映城市道路网的整体结构,还需保持道路网局部模式特征[1, 2, 3, 4]。其中格网街区是道路网中普遍存在的一类重要模式,指城市部分区域的道路呈现纵横相交的形态,而且格网街区的排列具有明显的规则性。这些特征在道路选取过程中应予以保持[5, 6, 7]。以往的道路选取研究集中于主干道选取和街区合并两类[8]。主干道选取通过复杂网络分析道路的重要性、划分道路等级并提取主干道[9, 10, 11]。但是该类方法的道路选取结果过于简化,属于城市整体结构,难以满足多尺度表达的需要;而街区合并方法则考虑街区密度、几何、语义等属性,通过局部渐进式方法删除街区边界道路、合并道路街区,减少道路密度[12, 13]。该类方法能在每次迭代中保持合并后道路街区的形态特点,但每次合并只考虑两个街区,对于解决多街区合并的形态保持问题尚有所不足。另外由于制图综合需求的复杂性,街区合并可能存在多种合理结果,局部合并方法缺少整体合并效果的评价准则,导致局部最优结果难以保证全局最优。文献[14]从整体出发提出一种地块合并的全局优化方法,根据合并后地块面积、形状、用地类型的变化建立了优化模型。相比于局部合并方法,优化算法可以考虑地图的全局特征,比邻域合并方法更能保持整体性。优化算法还可以通过目标函数的设定从多种备选方案中选取最优结果,比只能得到单一处理结果的局部合并更符合制图综合的特点。但是该方法的研究对象是土地利用地图数据,未考虑城市道路网的结构特征,不能直接用于街区合并简化。目前尚缺少针对城市道路格网模式保持的街区合并优化模型。本文从格网模式的提取和保持入手,构建相应的目标函数和约束条件,建立规划模型。通过求模型最优解,在街区合并过程中实现对道路格网模式的保持,以满足多尺度制图综合的需要。
2 道路格网模式的识别和特征分析
由于道路街区合并的目标是保持格网模式的形态和排列规则性,首先需要从原始道路网中检测出具有格网模式的街区(多边形)。根据街区合并建模的需要,本文的格网检测规则有两点:
(1) 紧密度。表示多边形形状的紧密程度,多边形的轮廓越复杂,紧密度越低。其计算公式为
紧密度的值域是(0,1],其中紧密度最高的为圆形,格网街区也应具有较高的紧密度。该指标主要用于排除主干道中的长条多边形。
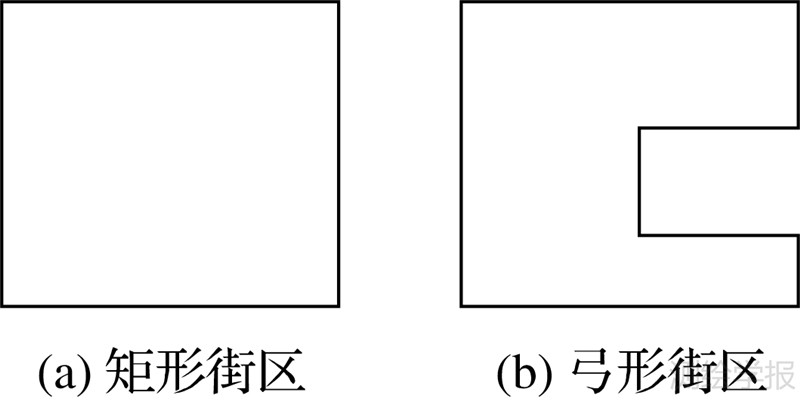
(2) 正交度。格网街区的边界方向大多相互正交,导致出现例如图 1所示的矩形和弓形两种街区形态。其中矩形街区反映格网模式的并列关系,而弓形街区反映包含关系。本文提出的正交度表示为多边形边界中正交道路占全部道路的比例。首先通过邻边比较遍历多边形的所有内角,当内角接近90°、180°和270°时,则将邻边聚为一类。为识别路网中变形的格网街区,可通过放松夹角阈值调整聚类结果,本文将其设为±15°。在道路聚类的基础上,正交度计算公式为
式中,ci(i=1,2,…,n)表示多边形的任一道路聚类;分子部分表示长度之和最大的道路聚类,而分母表示全部道路之和,即多边形的周长。正交度越大,表示多边形的格网模式特征越明显。
|
| 图 1 常见的格网街区结构 Fig. 1 Common grid blocks structures |
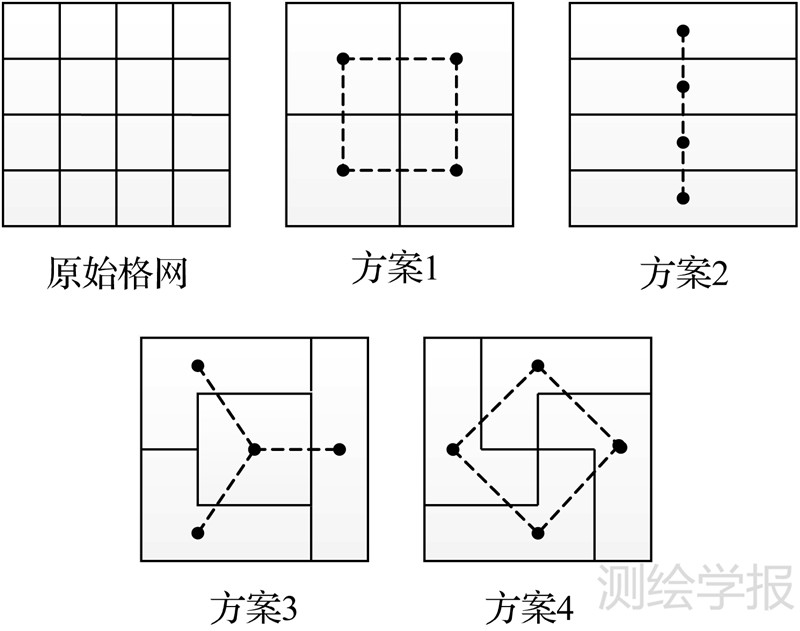
以上两点不仅是格网模式的检测规则,也是街区合并之后格网模式保持的评价规则。其中无论格网如何合并,街区的边界总是正交,因此重点是保持街区紧密度。此外格网模式还具有排列规则性和形态特征[6, 7]。其中排列规则性指格网街区通常规则地排成行列,而形态特征指在合并过程中应尽量保持格网模式的长宽比值。这需要避免只删除单一方向的道路,而是同时在长宽两个方向上删除道路。因此本文也将其称为合并的方向性。图 2为不同简化方案对于格网模式保持的示意图。假设原始数据为4×4标准方格网,方案1的合并结果具有最大的紧密度,并且保持了排列规则性和合并方向性。而后3种方案都无法同时保持格网模式的这3点特征。其中排列规则性评价为合并后相邻街区中心连线与公共边界的夹角。如图 2中的虚线段表示相邻格网中心点的连线,排列规则性需要保持中心点连线与格网公共边界道路尽可能的垂直。本文的街区合并优化模型通过设定评价函数量化各种格网模式,同时综合考虑被合并街区用地类型的相似性以及被删除道路的重要性,求解优化的合并结果。
|
| 图 2 格网街区合并方案示意图 Fig. 2 Example of grid-like blocks aggregation plans |
在建立目标函数对格网模式进行量化之前,首先定义变量xuv∈{0,1}指示道路网中的街区u与v是否合并。其中街区u定义为合并的中心街区,当v同u合并时,xuv=1,否则xuv=0。规定xuv=xvu及xuu=1,可将变量数目减少一半,提高计算效率。目标函数根据变量xuv建立格网模式保持的优化函数关系。通过求解使目标函数达到极值的xuv,便能得到街区合并结果。本文的目标函数为5个评价准则函数之和,包括用地类型相似性、街区紧密性、道路重要性、格网排列规则性和合并方向性。其中用地类型相似性和街区紧密性是一般性地块合并模型中都需要考虑的评价准则[14];道路重要性是本文针对于城市道路网整体结构特征保持所提出的评价准则;而格网排列规则性和合并方向性则是针对于道路网中的格网模式保持进一步提出的评价准则。每个评价准则的具体含义阐述如下。
3.1.1 用地类型相似性评价街区合并首先需要考虑合并之后用地类型的语义信息变化,相似类型的街区被合并的可能性更高[15]。本文将城市区域分为6种用地类型,包括水体、居民地、工业用地、农业用地、草地和森林。其中水体边界不被删除,而其他用地类型之间的合并代价如表 1所示[14]。用地类型相似性评价函数计算公式如下
式中,街区u、v∈P,P为多边形的集合;Cuv表示街区u和v之间的合并代价;Av表示街区v的面积。该函数通过使面积加权合并代价最小化,从语义层面引导用地类型相似的街区优先合并。| 居民地 | 工业用地 | 农业用地 | 草地 | 森林 | |
| 居民地 | 0 | 0.2 | 1 | 1 | 1 |
| 工业用地 | 0.2 | 0 | 1 | 1 | 1 |
| 农业用地 | 1 | 1 | 0 | 0.1 | 0.3 |
| 草地 | 1 | 1 | 0.1 | 0 | 0.3 |
| 森林 | 1 | 1 | 0.3 | 0.3 | 0 |
城市街区合并后一般很少出现复杂形状的街区,需要建立评价函数使合并后街区的紧密度之和最大化。由于式(1)计算的紧密度为非线性函数,难以计算模型最优解,本文建立近似的线性函数评价合并后街区的紧密度之和。文献[14]已证明当合并尺度确定时,被保留的道路长度越小,则合并后街区的紧密度就越高。因此本文的紧密性评价函数表示为合并后保留道路长度最小化,如式(4)所示。
式中,Luv表示街区u与v之间公共道路边界的长度,如果街区u与v之间没有公共道路,则lengthuv=0。而(1-xuv)表示道路是否被删除。该评价函数使得模型更倾向于得到使街区形状简单紧凑的街区合并方案。3.1.3 道路重要性评价
道路街区的合并还应保持道路网的整体结构特征,主要表现为道路的重要性[8, 9]。重要性高的道路应当被优先保留,这样可以反映城市区域的框架形态。根据格式塔原理,道路重要性评价通常以路划(stroke)作为基本评价单位。路划定义为由多条平滑道路链组成的长道路[16]。路划的长度越长,重要性越高,对体现道路网整体结构特征的作用也越大[17]。因此本文的道路重要性评价准则为使删除的路划长度最小化,即避免在街区合并过程中删除长路划。其中路划通过同名道路和平滑道路夹角进行提取。引入变量ys∈{0,1}表示第s条路划是否被删除,当被删除时ys=1。删除路划长度最小化评价函数的计算公式如下
式中,路划s∈S,S为所有路划的集合;Ls表示路划s的长度。而变量ys与xuv的关系可以表述为 式中,euv∈E表示街区u与v之间公共道路,体现了道路与街区之间的拓扑关系,E为所有的道路边集合;strs(euv)∈{0,1}为常量,表示道路euv是否属于路划s。如果euv属于路划s,则strs(euv)=1;当u与v之间公共道路e不属于路划s,或者u与v之间不存在公共道路时,则strs(euv)=0。式(6)可以保证在计算式(5)时,同一条被删除路划的长度只被计算一次。 3.1.4 排列规则性评价以上3点特征评价准则适用于所有道路街区。但对于道路格网街区,还需建立排列规则性的评价函数保持格网模式。由前节所述需要保持合并后街区的中心点连线与格网公共边界道路尽可能的垂直。本文通过计算合并前街区中心点连线与公共边界道路夹角余弦的面积加权之和,构建线性函数进行近似计算。定义i、j表示任意街区,euv为u、v街区的公共道路,ij和euv分别表示以街区i和j的中心点为起止点的向量和道路euv起止点构成的向量,夹角余弦计算公式如下
ij和euv的垂直度越高,则cos(ij,euv)越接近0。排列规则的格网此夹角余弦应尽量小,因此排列一致性评价函数计算公式为
式中,PG表示所有识别出的格网街区集合;EG表示格网街区的公共边界集合,这两个集合可在格网识别过程中建立;zeij∈{0,1}为新定义的变量,表示i、j、u、v四个格网街区之间的关系。当且仅当i与u合并,且j与v合并时,即当xui和xvj同时等于1时,zeij=1,否则为0。该规则可由式(9)得到保证
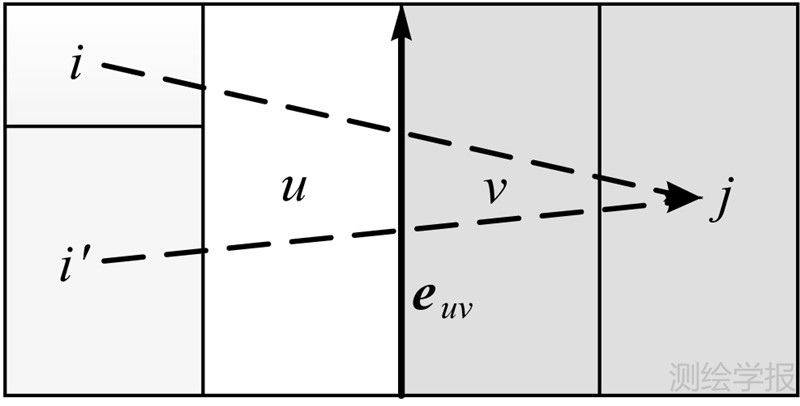
公式(8)的几何意义如图 3所示。假设图中左边街区i和i′与u合并,右边街区j与v合并,公式(8)中的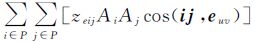 首先计算与u合并的所有街区(本例为i、i′)到与v合并的所有街区(本例为j)的所有向量与边界道路向量euv夹角余弦的面积加权之和。由于分列于euv垂线两侧的ij与i′j计算的余弦符号相反,求和后可以使合并后的街区中心连线与公共边界夹角余弦基本为0。而使用面积作为权值可以使街区合并前面积较大的原始街区占据主导作用。最后式(8)遍历区域内所有道路,计算每条道路两侧街区合并后的夹角余弦的绝对值,并以道路长度为权重求和。计算的值越小,合并后的街区排列规则性越高。如果道路euv在街区合并中被删除,即图 3中的街区u和v实际上合并为同一个街区,由于cos(ij,euv)+cos(ij,evu)≡0,则式(8)中以该条道路为边界计算的结果恒为零。这样可以保证合并后被删除的道路不被计算在内。
首先计算与u合并的所有街区(本例为i、i′)到与v合并的所有街区(本例为j)的所有向量与边界道路向量euv夹角余弦的面积加权之和。由于分列于euv垂线两侧的ij与i′j计算的余弦符号相反,求和后可以使合并后的街区中心连线与公共边界夹角余弦基本为0。而使用面积作为权值可以使街区合并前面积较大的原始街区占据主导作用。最后式(8)遍历区域内所有道路,计算每条道路两侧街区合并后的夹角余弦的绝对值,并以道路长度为权重求和。计算的值越小,合并后的街区排列规则性越高。如果道路euv在街区合并中被删除,即图 3中的街区u和v实际上合并为同一个街区,由于cos(ij,euv)+cos(ij,evu)≡0,则式(8)中以该条道路为边界计算的结果恒为零。这样可以保证合并后被删除的道路不被计算在内。
|
| 图 3 排列方向计算示意图 Fig. 3 Example of arrangement calculation |
对于格网街区还应当尽量在长宽两个方向上删除道路。本文计算简化前所有格网街区长宽方向道路长度比值,将合并方向性评价函数定义为合并前后的长宽比值差异最小化,计算公式如下
式中,E1和E2分别表示简化前格网街区在两个正交方向上的道路集合,可在格网识别中计算正交度时求得。r0表示简化前的正交方向比值。最优的格网合并方案应当尽量使式(10)取值最小,这样便能保持合并前后正交方向道路长度的比值关系。根据每个评价函数的定义,通过将公式中的变量xuv、ys、zeij去除后的求和结果作为分母对各个评价函数进行归一化,将上述五项评价函数的值域归一化为[0, 1]。最终的目标函数为5个评价函数之和。可以看出对于非格网街区,其排列规则性和合并方向性评价函数均为零。路网中的格网街区比例越大,则后两个评价函数所占的比重也就越大。因此,虽然本文模型主要适用于格网街区的合并,但对于城市范围内其他类型的街区,也可简化为只依靠前三项评价函数进行建模。
3.2 约束条件 3.2.1 合并尺度约束为使街区进行合并,但又不出现过度合并,应当设定合并后的最小和最大面积阈值。合并尺度约束公式如下
式中,Amin和Amax分别表示街区合并的最小和最大面积阈值;max(Amax,Au)表示如果街区u的面积在合并之前就已经大于Amax,则不对其进行合并,如果Amin和Amax之间出现冲突,例如一个面积小于Amin的街区仅与一个面积大于Amax的街区相邻,则这两个街区无论合并与否都不能同时满足公式(11)中的两个约束条件。因此设置宽松项δ和步长k∈{0,1,2,…,n},当面积阈值冲突时逐步放大最大阈值直至冲突解决。本文将δ设为最小面积阈值Amin。最小面积阈值Amin可根据地图中最小可视元(smallest visible object,SVO)进行设定。SVO的面积受线划宽度、街区内含建筑物等多方面影响,需参照具体制图规范,或根据经验和数据分析确定[18]。简便起见,本文认为已有的初始尺度数据中的最小街区为该尺度下的SVO。而目标尺度下最小面积阈值Amin则设为初始尺度SVO面积乘以简化前后比例尺变化率的平方,如式(12)所示。
例如本文街区合并的目标是由1∶25 000简化至1∶100 000,比例尺变化率为4,表示地图上SVO的长度扩大4倍,则最小面积阈值为当前SVO面积的16倍。
最大面积阈值Amax设为与区域内所有街区面积均值成正比,如式(13)所示。
式中,A表示区域中所有街区面积的平均值;f是一个人工设定的比率因子,用于控制合并的程度。如将街区合并模型分别独立应用于城市中的多个分区时,式(13)还可一定程度上控制分区之间的密度差异。如果街区合并前已有多尺度数据的经验信息,Amax阈值也可根据其他规则进行约束[13, 19]。 3.2.2 路划删除约束根据道路等级性评价准则,在街区合并过程中应以路划为基本单位,保持路划整体删除或者保留,防止破坏道路形态。路划删除约束公式如下
式(14)表示当道路段eu1v1、eu2v2、…、eukvk都属于同一条路划STRs时,则这些路段两侧的街区将被同时合并或保留。如果删除路划的某段会导致格网面积大与最大阈值时,可以保留该段道路。
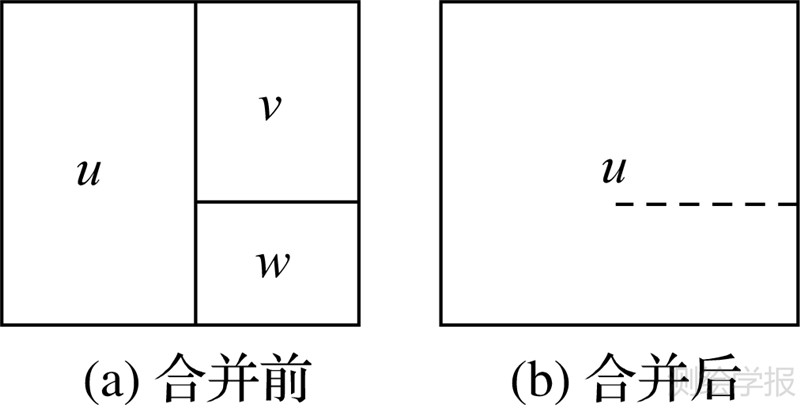
3.2.3 道路联动删除约束如图 4所示,当相邻街区v和w分别和街区u合并,那么街区v和w之间的公共边界(虚线道路)也应当被联动删除,联动删除的计算公式如下
式(15)能够保证3个相关变量xuv、xuw、xvw不会出现两个取值为1,一个为0的情况,从而保证了道路删除的联动性。
|
| 图 4 道路联动删除示意图 Fig. 4 Example of conjoint road deletion |
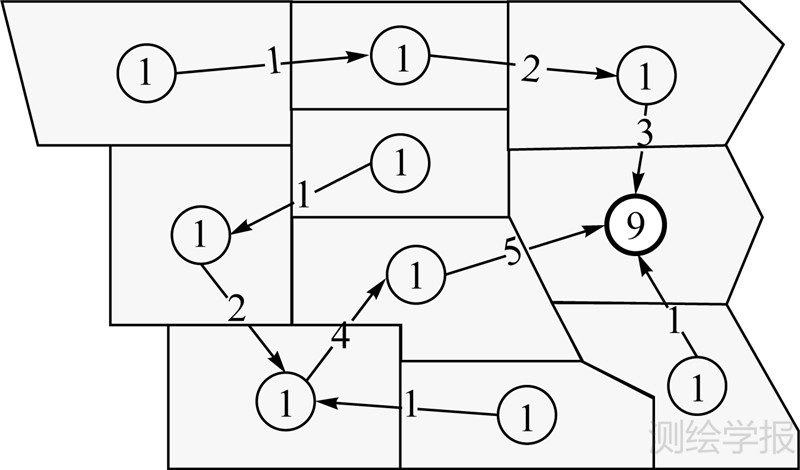
街区合并过程还需要保证合并街区的连通性,即不存在隔空合并。本文根据流模型建立约束条件,基本原则如图 5所示[19]。其中非中心街区用细圆圈表示,初始量设为1;粗圆圈为指定的某个中心街区,表示所有流的最终汇入点,无初始量。箭头表示自由构建的连通流。每个非中心街区都有且只有一个输出流,流量大小等于输入流加上街区自身的初始量;而中心街区只有输入流,最终的汇入量不超过非中心街区数。如果合并后的街区中构建的流模型满足上述约束条件,则认为街区合并是连通的。
|
| 图 5 连通性约束示意图 Fig. 5 Example of connectivity constrain |
为构建流模型,引入新的非负的连续变量tuvw,表示当u为中心街区时,街区v向邻接街区w的输出流。同理tuwv则表示来自街区w流向v的输入流,连通性约束条件如式(16)—式(18)所示。
式中,M是一个非负整数,表示合并过程中所允许的最大街区数。如果M设为所有街区总数,表示无街区合并数的约束,式(18)可以删除。xuv的定义与之前一致,用于表示街区v与u是否合并。式(16)表达了每个非中心格网v的净流量,等式左边的两项分别表示格网v的总输出流和总输入流。如果格网v与中心格网u合并,那么xuv=1,则总净流量必须等于1,表示流模型中与v连通的所有上级街区都被输送到下一级街区。式(17)表示每个非中心街区v的总输入流不能超过M-2,即允许合并的最大街区数减去自身和中心街区u。式(18)表示中心街区u的总输入流不能超过最大街区数减去自身。结合式(16)和式(17)可知,如果街区v不与u合并,则街区v的输入流和输出流都为零,即没有未合并的街区流入合并集合中,也没有合并集中的街区流出到集合外。 3.3 模型求解本文的街区合并模型中的变量分别为xuv、yi、zeij和tuvw,其中前三项的值域为0-1整数,tuvw为非负实数。所有的评价函数和约束函数都是线性函数,其中式(8)和式(10)中绝对值可以转化成线性形式。因此本文所构建的模型属于混合整数规划模型(mixed integer programming,MIP)。常用的混合整数规划模型的求解方法是“分支约束”的方法。本文采用该方法,通过使用IBM ILOG CPLEX软件求解混合整数规划模型。该软件运算性能高,支持多CPU,并且算法稳健,对模型中方程和变量数目的支持能力仅取决于计算机的硬件水平。
4 高等级道路提取和路网分区在道路选取过程中除了保持格网模式特征之外,还需要保证高等级道路在街区合并时不能被删除,即保持道路网主干道的整体结构特征。高等级道路还能间接保持道路网中一些其他结构模式。例如放射状结构是道路网中一种比整体结构更概括的特征结构,可以在高等级道路和城市中心模式识别的基础上进行提取[1, 3]。二者存在一种包含关系,保持了道路的骨架结构也就间接保持了放射状结构。当放射状结构尺度较小时,则可根据前面所提的道路重要性评价准则优先选取长路划进行控制。
本文使用中介中心性(betweenness centrality,BC)提取道路网的高等级道路。该指标能够较全面地反映道路网的整体结构特征[20, 21]。BC定义为某条道路被任意两条连通道路之间的最短连通路径所经过的次数,反映了道路被其他道路所依赖的程度[22]。BC值越大,道路的重要性越高。BC值具有指数分布特征,少量道路具有极高的BC值,可以通过设定阈值选取高等级道路,构造道路网的整体结构特征。基于道路网整体结构,还可将城市划分为多个区域,对每个分区内部分别进行建模。既保持了道路网整体结构不被破坏,又减少了合并模型的复杂度。由于模型以路划为取舍单位,当一条路划穿过多个分区时,则将这些分区作为一个整体进行建模,保证各个分区内部的道路选取互不干扰。
5 试验结果与分析试验数据使用德国汉诺威ATKIS-DLM 1∶25 000的数据,将尺度综合至1∶100 000。经过数据预处理的结果如图 6所示,黑色道路表示的是根据BC>100 000选取的高等级道路,其中粗线表示人工从中选取的放射状结构。可以看出高等级道路能够体现出道路网的整体结构和隐含的结构形态。灰色街区表示的是根据紧密度和正交度识别出来的格网模式,阈值分别为0.45和0.7。可以看出格网街区在城市道路网中的普遍性。利用高等级道路对道路网进行分区,然后对每个区域单独进行街区合并建模。原始数据中最小街区面积约为150 m2,则areamin参数设置为2400 m2。areamax中的f根据经验设为3.5,表示每个分区内街区合并的面积上限是平均面积的3.5倍。
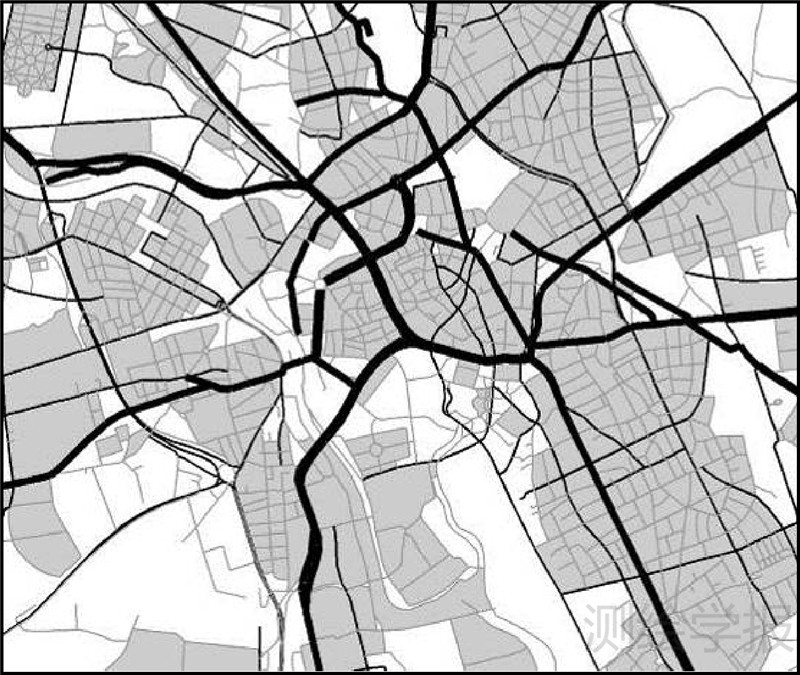
|
| 图 6 道路格网识别与分区(BC>100 000) Fig. 6 Grid-like blocks recognition and partition (BC>100 000) |
图 7为综合各个分区街区合并之后得到的街区合并结果以及与同时期德国1∶100 000地形图的比较,其中街区合并之后长度小于300 m的悬挂道路被删除。各个用地类型用不同颜色表示,黑色道路表示两份数据中都被保留的道路,而灰色表示都被删除的道路;黑色虚线道路表示本文结果比已有图多出的道路,而灰色虚线道路表示已有图比本文结果多出的道路。首先从直观分析可以看出本文的道路选取结果很好地保持了道路网整体的城市结构、局部的格网排列一致性以及区域之间的密度差别。
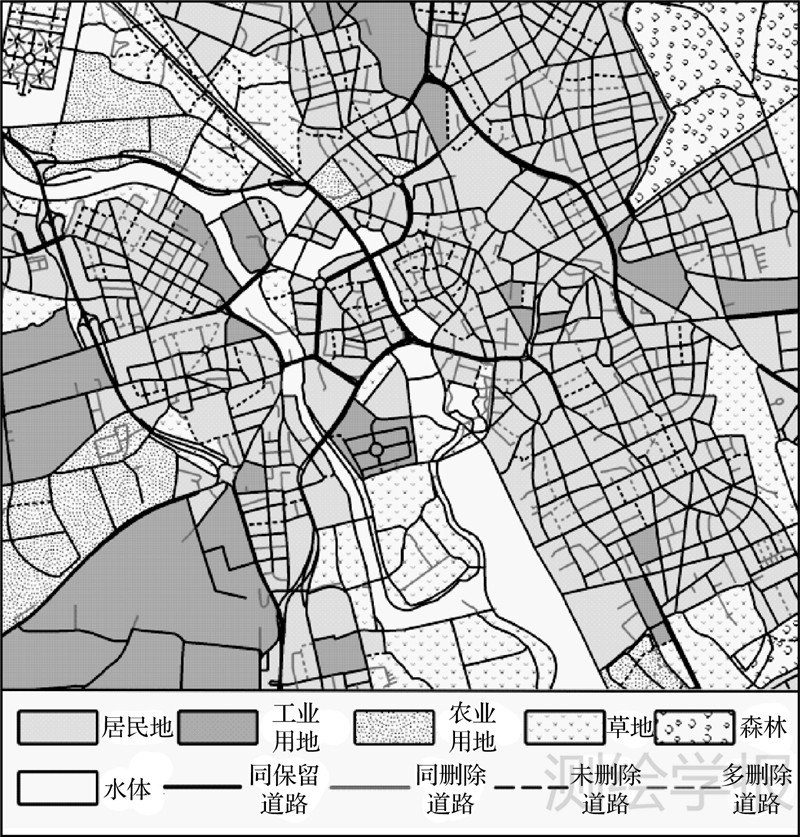
|
| 图 7 道路选取结果及与已有图比较 Fig. 7 Roads selection results compared with existing map |
与图 7相对应,对本文试验结果中保留与舍弃的道路以及两种原始数据中的道路长度进行统计。统计结果如表 2所示。
| m | |||||
| 1∶2.5万 地图简化 |
| ||||
| 选取道路 | 457 411(黑) | 34 190(黑虚) | 93.05 |
| 合并道路 | 19 460(灰虚) | 80 423(灰) | 80.52 |
| 查全率/(%) | 95.92 | 70.17 | 90.93 |
从统计数据分析发现本文模型具有以下特点:
(1) 本文试验结果与已有的地图数据相比,正确率和查全率都较高,说明本文模型与人工的道路选取结果基本相符。
(2) 统计发现本文模型未删除的道路(黑色虚线道路)要明显多于本文模型多删除的道路(灰色虚线道路)。部分未删除道路由于两侧街区面积较大,或路划长度较长,受面积或路划长度约束未进行合并。这部分道路主要位于草地、森林和农业用地中,约占未删除道路总数的37%,因为道路重要性较低而被人工删除,另有部分未删除道路作为某些长路划的一部分被整体保留。而在人工选取中考虑到语义信息,部分删除了一些路划。这部分道路主要位于居民地街区中,约占未删除道路总数的29%。这种差异主要是由于地图简化规则不同。本文模型保留的这些道路不会影响地图的可读性,还保持了地图的信息量。因此认为本模型在这些道路的保留上也是合理的。
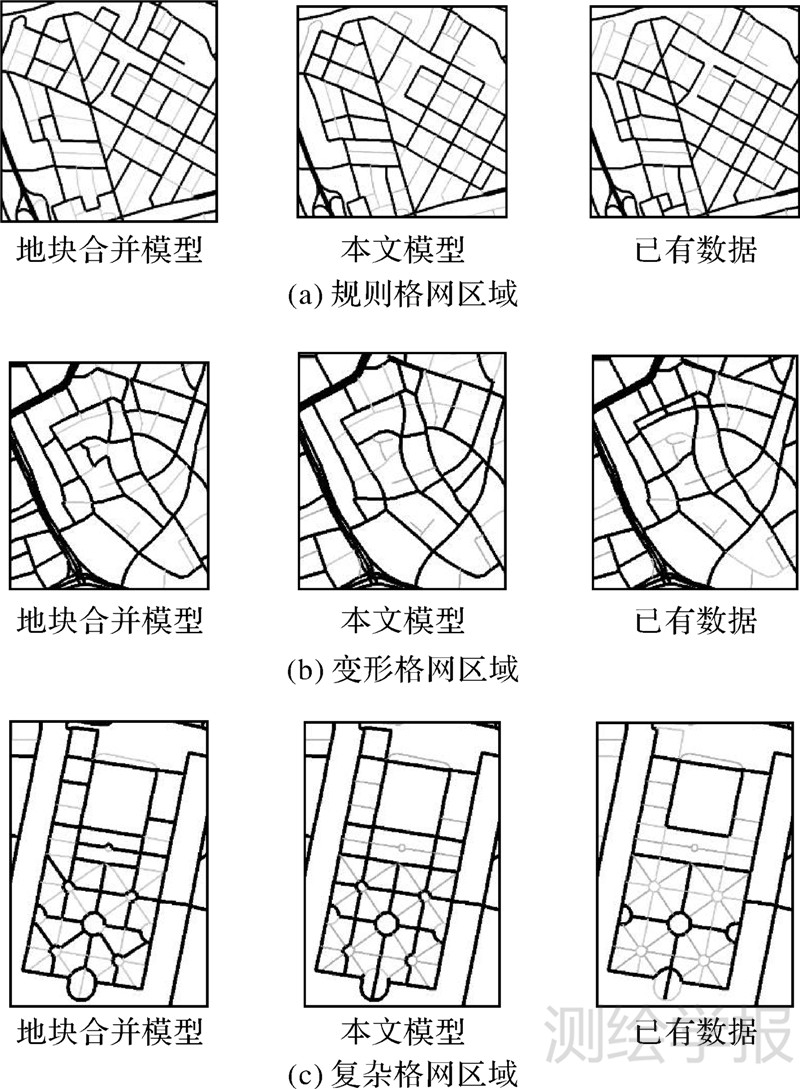
(3) 本文模型在某些区域保留了一些人工删除的道路,却删除了一些人工保留的道路,模型构造的街区形态与已有数据存在差异。这部分道路主要分布在居民地街区中,约占未删除道路总数的22%。但是相应的多删除道路却占到多删除道路总数的91%,说明本文模型产生的多删除道路主要产生于此。差异产生的原因需分析具体的合并细节。同时,为了展示本文模型的评价和约束规则对格网模式保持的影响,本文还与文献[14]中的地块合并模型进行了细节对比。该模型仅使用紧密度和用地类型相似性作为目标函数,未考虑道路网的结构特点。图 8展示了3块区域的比较,其中图 8(a)是较规则格网区域,图 8(b)是有道路弯曲的变形格网区域,图 8(c)的结构则较复杂,只有在合并之后才能呈现格网形态。
|
| 图 8 不同合并模型比较 Fig. 8 Comparison of different aggregation models |
对于图 8(a)的规则格网区域,3种合并结果在街区面积变化、形状变化和数目变化都相似,而且都大体保持了街区格网模式。这是因为规则格网区域中无论如何合并总能保持道路正交,但是由于缺少格网排列评价准则,一般的地块合并模型不如本文模型合并的街区排列规则。对于图 8(b)和8(c)的变形和复杂格网区域,一般的地块合并模型已经无法保证合并街区的形态,而本文模型能够较好保持住合并后街区的规则排列和长宽比形态。
本文模型与已有数据中的人工选取结果相比,二者都保持了道路网的结构形态。主要差异在于本文模型保留了区域中的长路划。由于保留的更多的道路,本文合并后的街区面积要小于人工选取结果,但保留的道路看上去更加连贯。而人工选取则体现出一种更加复杂的道路网结构感知,体现了地图综合的多样性和复杂性。虽然存在部分差异,但是相比手工选取,自动的道路选取方法效率更高。因为人工进行选取时,需经常检查道路的整体和局部模式特征,效率很低。因此本文模型对于提高地图生产效率和质量具有重要的作用。
6 结束语本文针对城市道路网的结构模式特征,在格网模式保持分析的基础上,提出了一种保持区域格网模式特征的街区合并模型。试验分析表明,本文模型通过建立街区合并的特征评价函数和约束规则能够保持街区所具有的格网模式特征。通过与人工道路选取的地图的对比分析,发现本文的方法得到的道路选取能较好地反映道路网的模式特征,正确率高于90%。但是由于本文方法主要从道路网的模式结构保持的角度出发,只研究了道路网数据,尚未考虑与道路网存在关联和依赖关系的其他数据,例如地形、建筑物、城市设施等,使得本文方法和人工的道路选取结果不可避免地存在差异性。考虑如何利用语义信息合并模型进行优化是后续的研究工作的重点。
| [1] | ZHANG Q N. Modeling Structure and Patterns in Road Network Generalization[C]//Proceedings of ICA Workshop on Generalization and Multiple Representation. Leicester: [s.n.], 2004. |
| [2] | HEINZLE F, ANDERS K H, SESTER M. Graph Based Approaches for Recognition of Patterns and Implicit Information in Road Networks[C]//Proceedings of XXII International Cartographic Conference. La Coruna: [s.n.], 2005. |
| [3] | HEINZLE F, ANDERS K H, SESTER M. Pattern Recognition in Road Networks on the Example of Circular Road Detection[C]//Geographic Information Science: Proceedings of 4th International Conference on GIScience. Münster: Springer, 2006: 153-167. |
| [4] | HEINZLE F, ANDERS K H. Characterising Space via Pattern Recognition Techniques: Identifying Patterns in Road Networks[C]//The Generalisation of Geographic Information: Cartographic Modelling and Applications [M]. Amsterdam: Elsevier, 2007: 233-253. |
| [5] | YANG Bisheng, LUAN Xuechen. An Automated Method for Structural Pattern Recognition of Road Networks [J]. Journal of Image and Graphics, 2009, 14(7): 1251-1255. (杨必胜, 栾学晨. 城市道路网几何结构模式的自动识别方法[J]. 中国图象图形学报, 2009,14(7): 1251-1255.) |
| [6] | YANG B S, LUAN X C, LI Q Q. An Adaptive Method for Identifying the Spatial Patterns in Road Networks[J]. Computers, Environment and Urban Systems, 2010, 34(1): 40-48. |
| [7] | TIAN Jing, AI Tinghua, DING Shaojun. Grid Pattern Recognition in Road Networks Based on C4.5 Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 121-126. (田晶, 艾廷华, 丁绍军. 基于C4.5算法的道路网网格模式识别[J]. 测绘学报, 2012, 41(1): 121-126.) |
| [8] | TOUYA G. A Road Network Selection Process Based on Data Enrichment and Structure Detection[J].Transactions in GIS, 2010, 14(5): 595-614. |
| [9] | JIANG B, CLARAMUNT C. A Structural Approach to the Model Generalization of an Urban Street Network [J]. GeoInformatica, 2002, 8(2): 157-171. |
| [10] | PORTA S, CRUCITTI P, LATORA V. The Network Analysis of Urban Streets: A Dual Approach[J]. Physica A: Statistical Mechanics and Its Applications, 2006, 369(2): 853-866. |
| [11] | YANG B S, LUAN X C, Li Q Q. Generating Hierarchical Strokes from Urban Street Networks Based on Spatial Pattern Recognition[J]. International Journal of Geographical Information Science, 2011, 25(12): 2025-2050. |
| [12] | HU Yungang, CHEN Jun, LI Zhilin, et al. Selective Omission of Road Features Based on Mesh Density for Digital Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36 (3): 351-357. (胡云岗, 陈军, 李志林, 等. 基于网眼密度的道路选取方法[J]. 测绘学报, 2007, 36(3): 351-357.) |
| [13] | YANG Bisheng, ZHANG Yunfei, LUAN Xuechen. Pattern Preserving Method for Grid Simplification in Road Networks[J]. Journal of Image and Graphics, 2012, 17(1): 150-156. (杨必胜, 张云菲, 栾学晨. 保持几何模式的城市道路格网简化方法[J]. 中国图象图形学报, 2012, 17(1): 150-156.) |
| [14] | HAUNERT J H, WOLFF A. Area Aggregation in Map Generalisation by Mixed-integer Programming[J].International Journal of Geographical Information Science, 2010, 24(12): 1871-1897. |
| [15] | LIU Y L, MOLENAAR M, KRAAK M J. Semantic Similarity Evaluation Model in Categorical Database Generalization[R]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Ottawa: ISPRS, 2002: 279-285. |
| [16] | XU Zhu, LIU Caifeng, ZHANG Hong, et al. Road Selection Based on Evaluation of Stroke Network Functionality[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 769-776. (徐柱, 刘彩凤, 张红, 等. 基于路划网络功能的道路选取方法[J]. 测绘学报, 2012, 41(5): 769-776.) |
| [17] | THOMSON R C. The ‘Stroke’ Concept in Geographic Network Generalization and Analysis[C] //Progress in Spatial Data Handling: 12th International Symposium on Spatial Data Handling. Vienna: [s. n.], 2006: 681-697. |
| [18] | CHEN J, HU Y G, LI Z L, et al. Selective Omission of Road Features Based on Mesh Density for Automatic Map Generalization [J]. International Journal of Geographical Information Science, 2009, 23(8): 1013-1032. |
| [19] | SHIRABE T. A Model of Contiguity for Spatial Unit Allocation[J]. Geographical Analysis, 2005, 37(1): 2-16. |
| [20] | LI Qingquan, ZENG Zhe, YANG Bisheng, et al. Betweenness Centrality Analysis for Urban Road Networks[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 37-41. (李清泉, 曾喆, 杨必胜, 等. 城市道路网络的中介中心性分析[J]. 武汉大学学报: 信息科学版, 2010, 35(1): 37-41.) |
| [21] | TOMKO M, WINTER S, CLARAMUNT C. Experiential Hierarchies of Streets[J]. Computers, Environment and Urban Systems, 2008, 32(1): 41-52. |
| [22] | FREEMAN L C. Centrality in Social Networks: Conceptual Clarification[J]. Social Networks, 1979, 1(3): 215-239. |