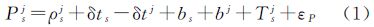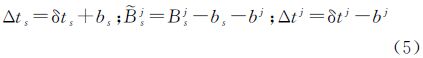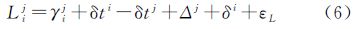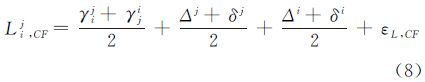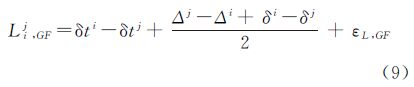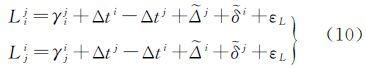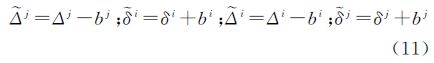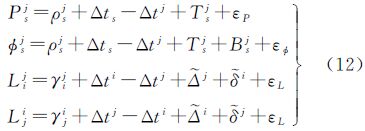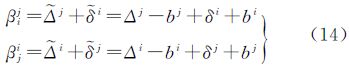2. 西安测绘研究所,陕西 西安 710054
2. Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China
1 引 言
北斗区域卫星导航系统已经于2012年底正式投入运行,但是北斗卫星导航系统的跟踪站一般只限中国境内,影响了卫星轨道的测定精度[1, 2]。目前各主要导航卫星系统(包括GPS、GLONASS、GALILEO和北斗)都积极开展星间链路及相关应用研究[3, 4, 5, 6]。对于那些无法在全球布设地面监测网的导航卫星系统,大量仿真研究结果表明,联合使用星地和星间链路数据是大幅度提高轨道及钟差确定精度的有效手段[7, 8, 9]。
设备时延是指信号通过电子设备时产生的附加时延,通常包括固定延迟部分和随温度、环境等变化的部分。设备时延绝对值不可测量[10, 11],往往与钟差参数无法分离,传统的基于伪距/相位数据的轨道及钟差解算中,接收机和卫星的设备时延分别叠加到各自的钟差中[12]。
由于星间测距信号与下行导航信号在频率和信号调制上都有很大差异,导致不同类型观测量所包含的设备时延不一致,必然以系统误差的形式影响联合定轨和钟差解算结果。目前有关联合星间链路数据进行定轨的仿真研究,有的忽略设备时延存在,有的仅考虑小量级的设备时延误差,且没有对其影响进行深入分析[7, 8, 9];有学者试图通过硬件标定的方法加以解决[13],但该方法只能测定收发设备时延之和以及不同接收(或发射)设备时延之差,无法建立星间链路设备时延与下行导航信号设备时延的关系,并不能解决设备时延的不一致问题。为此本文针对星间链路设备时延问题展开讨论,提出在定轨和钟差解算的同时估计设备时延参数,以期最大限度地降低设备时延的影响。
2 测量方程 2.1 伪距和相位测量方程导航卫星系统一般采用地面监测网观测伪距和相位,以此作为精密定轨和钟差解算的基本观测量,并采用双频组合消除电离层延迟影响,观测量可表示如下[14]
式中,Psj、Φsj为接收机s对卫星j的伪距和相位双频消电离层组合观测量;ρsj=|rs-rj|为信号从卫星j传播到接收机s经过的距离;rs为接收机位置向量;rj为卫星位置向量;εP、εΦ为伪距和相位组合观测量噪声;δts为接收机钟差;δtj为卫星钟差; bj为卫星伪距设备时延(也叫群时延);bs为接收机伪距设备时延;Tsj为信号传播路径的对流层延迟;Bsj为相位偏差,包含了相位模糊度、卫星和接收机的相位设备时延及非零初始相位的影响[14](本文中符号单位为m)。导航信号设备时延的绝对值不可测[10],在精密定轨和钟差解算时,叠加到卫星钟差当中。因此卫星钟差包含了卫星导航信号设备群时延,导航卫星广播的卫星钟差改正数亦如此[12]。在实际的数据处理中,式(1)和式(2)应该写成
式中 Δtj是地面监测网数据可测的卫星钟差,也是用户实际可用的卫星钟差。 2.2 星间伪距测量方程导航卫星按照链路规划采用时分多址的方式进行星间通信和测距[15, 16]。以GPS BLOCK IIR卫星(24颗)的星间链路为例:一个测量时帧为36 s,每颗卫星在所分配的1.5 s轮循时隙内广播星间测距信号,在其余23个时隙侦测其他卫星广播的星间测距信号。如此,一颗卫星要花整个时帧才能获得对所有可测卫星的测距值,且这些测距值的观测时刻是各不相同的。这与地面接收机获得伪距和相位观测量的方式截然不同,后者总是同时获得对所有可见卫星的观测量。在数据处理时,为了方便,通常将一个观测周期内收到的不同卫星的星间测距观测量归化到同一时刻上,称为历元归化[17, 18]。这里不对历元归化方法展开讨论,直接给出历元归化后的星间测距观测量的数学表达式[17, 18]
式中,Lij为卫星i观测到卫星j (j≠i)的测距值;γij=|ri-rj|为卫星j到卫星i的几何距离;δt为卫星钟差,上标i表示对应的卫星号;Δ、δ为星间链路发射和接收设备时延,上标表示卫星号;εL为测量噪声,包含了设备时延不确定性和历元归化引起的误差。在实际应用中有两种组合观测量比较常用,分别称为无钟差(clock free)组合和无几何(geometry free)组合
式(8)消除了卫星钟差信息,只能用于定轨;式(9)中没有距离信息,只能用于钟差解算。
利用同一颗卫星的星间链路接收和发射信号进行闭环测量,可以测得收发设备时延之和Δj+δj;将不同卫星的发射设备(或接收设备)与同一接收设备(或发射设备)进行测量,可以测得不同卫星同类设备时延之差Δj-Δi(或δi-δj)。文献[11]在讨论伪距和设备时延的关系时也指出这一点。将以上测量结果代入式(8)和式(9),设备时延问题似乎已经迎刃而解。
然而,导航卫星系统不必也无法从卫星钟差中分离出导航信号群时延[10],用户定位和授时所采用的卫星钟差包含了下行导航信号群时延,直接利用式(9)解算得到的卫星钟差(虽然反映了卫星的真实钟差)并不能直接应用于用户定位和授时计算。为了保持与用户算法的一致性,利用星间测距数据求解的卫星钟差也应该包含下行导航信号群时延(下文的“卫星钟差”皆指包含下行导航信号群时延的钟差)。式(5)代入式(6)和式(7),用于星地/星间联合定轨的星间测距观测方程应写成
式中
 、
、 分别为星间链路发射和接收时延改正数(简称时延改正数),它们是星间链路设备时延与下行导航信号群时延的线性组合,需要与卫星轨道、钟差等参数一并求解。
分别为星间链路发射和接收时延改正数(简称时延改正数),它们是星间链路设备时延与下行导航信号群时延的线性组合,需要与卫星轨道、钟差等参数一并求解。
方程(10)中时延改正数与卫星钟差参数线性相关,只有在卫星钟差已知或者有地面网观测数据参与的情况下才能求解。容易想到以下两种数据处理策略:一是单独利用星间测距测量,固定卫星轨道和钟差求解时延改正数或仅固定卫星钟差同时求解轨道和时延改正数;二是联合伪距(相位)和星间测距观测量同时求解卫星轨道、钟差和时延改正数。策略二可充分利用星间测距信息,获得卫星轨道、钟差及时延改正数的最优解。考虑到时延改正数数量不多(每颗卫星2个),这样做不会明显增加数据处理的难度和复杂性,笔者推荐采用策略二。联合观测方程可表示如下
需要指出的是:即使在卫星钟差已知的情况下,由观测方程(12)构成的法方程也是秩亏的,秩亏数是1,这意味着 和
和 的绝对值是不可测的,或者说时延改正数的数值与选择的参考有关。对于法方程秩亏的处理,可以采用两种方法(同样适用于采用策略一的数据处理):
的绝对值是不可测的,或者说时延改正数的数值与选择的参考有关。对于法方程秩亏的处理,可以采用两种方法(同样适用于采用策略一的数据处理):
(1) 选取一个时延改正数做参考,对其进行约束,正如处理钟差参数那样[19]。这样得到的时延改正数估值实际上是相对值,但这并不会影响使用,可以直接代入式(10),或代替式(8)和式(9)中的Δ、δ。
(2) 将每一条链路的发射和接收时延改正数合并成一个链路时延改正数,构成如下形式的联合观测方程
式中
在卫星钟差已知(或有星地链路参与)的情况下,每条链路的时延改正数βij是可测的。因为链路数可能会达到几百条,这样得到βij和βji的估计结果,显然不如 、
、 方便应用。
方便应用。
方法(1)适合于“一对多”模式的星间链路,如GPS BLOCK IIR的UHF模式的星间链路[15];方法(2)更适合于“一对一”模式的星间链路,例如静态链路[20]。
4 仿真分析 4.1 试验设计为了验证以上方法的效果,利用自主研发的星地/星间链路数据处理和仿真软件进行了仿真试验。基本仿真条件如下:
星座:MEO Walker 24/3/1∶55°;
地面站:7个监测站(北京、哈尔滨、成都、三亚、汕头、乌鲁木齐、喀什);
星地链路:伪距和相位观测精度分别为0.3 m和2 mm;
星间链路:宽波束(类似于GPS BLOCK IIR卫星采用的UHF模式),信号波束地心夹角15°~60°;
钟差:采用0均值白噪声模拟,接收机和卫星钟差噪声标准差分别为10 μs和1 μs;
采样间隔:300 s;
数据弧段:3 d;
设备时延:星间链路发射和接收设备时延,下行导航信号设备时延由FORTRAN编译器自带的 RANDOM函数生成0~0.3 m均匀分布的随机数,如表 1所示。
| m | |||
| ID | Δ | δ | b |
| 01 | 0.242 | 0.152 | 0.066 |
| 02 | 0.126 | 0.240 | 0.259 |
| 03 | 0.262 | 0.299 | 0.097 |
| 04 | 0.110 | 0.002 | 0.016 |
| 05 | 0.242 | 0.086 | 0.285 |
| 06 | 0.062 | 0.128 | 0.272 |
| 07 | 0.276 | 0.132 | 0.070 |
| 08 | 0.114 | 0.178 | 0.283 |
| 09 | 0.269 | 0.023 | 0.042 |
| 10 | 0.028 | 0.147 | 0.127 |
| 11 | 0.198 | 0.227 | 0.023 |
| 12 | 0.071 | 0.119 | 0.164 |
| 13 | 0.083 | 0.268 | 0.053 |
| 14 | 0.196 | 0.284 | 0.045 |
| 15 | 0.256 | 0.110 | 0.022 |
| 16 | 0.097 | 0.288 | 0.221 |
| 17 | 0.224 | 0.244 | 0.051 |
| 18 | 0.046 | 0.147 | 0.169 |
| 19 | 0.155 | 0.024 | 0.064 |
| 20 | 0.189 | 0.017 | 0.088 |
| 21 | 0.298 | 0.097 | 0.196 |
| 22 | 0.153 | 0.115 | 0.005 |
| 23 | 0.036 | 0.030 | 0.097 |
| 24 | 0.224 | 0.138 | 0.265 |
基于以上基本条件,仿真生成不同星间测距精度的3组数据:
数据1:星间测距精度1.0 m;
数据2:星间测距精度0.3 m;
数据3:星间测距精度0.1 m。
对每一组数据,按照仿真输入条件对不同类型观测量进行赋权,分别采用以下4种不同方案进行定轨和钟差解算处理:
方案1:忽略设备时延,直接将数据用于定轨和钟差解算;
方案2:利用表 1的设备时延值对观测量进行改正,然后用于定轨和钟差解算,得到理想的结果,用作参考以评价方案3和方案4的效果;
方案3:在解算卫星轨道和钟差的同时估计每颗卫星的发射和接收时延改正数,3 d估计1个值;
方案4:在解算卫星轨道和钟差的同时估计每条有向链路的时延改正数,3 d估计1个值。
每组数据分别得到1组(由方案3得到)卫星时延改正数估计结果、1组链路改正数估计结果(由方案4得到)和4组轨道和钟差解算结果。
4.2 卫星时延改正数估计结果
表 2列出了1—8号星时延改正数 和
和 的理论值(利用表 1数据由式(11)计算得到)、数据1得到的估计值及其误差。数据处理时,选取1号星的接收时延改正数为参考,因此1号星接收时延改正
的理论值(利用表 1数据由式(11)计算得到)、数据1得到的估计值及其误差。数据处理时,选取1号星的接收时延改正数为参考,因此1号星接收时延改正 的估值与真值的偏差为-0.218 m,即为系统性误差。而其他各颗卫星的时延改正数
的估值与真值的偏差为-0.218 m,即为系统性误差。而其他各颗卫星的时延改正数 和
和 的估值分别有量级相当,符号相反的系统性偏差。同一卫星的时延改正数
的估值分别有量级相当,符号相反的系统性偏差。同一卫星的时延改正数 和
和 的估计误差似有负相关关系。
的估计误差似有负相关关系。
| m | |||||||
| PRN |  | 
| |||||
| 真值 | 估值 | 误差 | 真值 | 估值 | 误差 | ||
| 01 | 0.218 | 0.000 | -0.218 | 0.176 | 0.413 | 0.237 | |
| 02 | 0.499 | 0.261 | -0.239 | -0.133 | 0.100 | 0.233 | |
| 03 | 0.396 | 0.154 | -0.242 | 0.165 | 0.422 | 0.257 | |
| 04 | 0.018 | -0.273 | -0.291 | 0.094 | 0.354 | 0.260 | |
| 05 | 0.371 | 0.160 | -0.211 | -0.043 | 0.154 | 0.197 | |
| 06 | 0.400 | 0.200 | -0.200 | -0.210 | 0.013 | 0.223 | |
| 07 | 0.202 | -0.045 | -0.247 | 0.206 | 0.441 | 0.235 | |
| 08 | 0.461 | 0.245 | -0.216 | -0.169 | 0.037 | 0.206 | |
表 3统计了时延改正数估值的平均误差和标准差。可以看出 和
和 的平均误差接近于理论值-0.218 m和0.218 m,差别在0.02 m以内。从标准差来看,数据1到数据3时延改正数估值的标准差随着星间测距精度的提高而递减。
的平均误差接近于理论值-0.218 m和0.218 m,差别在0.02 m以内。从标准差来看,数据1到数据3时延改正数估值的标准差随着星间测距精度的提高而递减。
| m | |||||
| MEAN | STD | ||||
 |  |  |  | ||
| 数据1 | -0.236 | 0.230 | 0.040 | 0.033 | |
| 数据2 | -0.231 | 0.226 | 0.029 | 0.027 | |
| 数据3 | -0.228 | 0.230 | 0.025 | 0.025 | |
仿真试验中,每颗卫星与20颗卫星建立了测距链路,(单向)链路总计480条。表 4给出了部分链路时延改正数的理论值(利用表 1输入的设备时延值,由式(14)计算得到)、数据1得到的估计值及其误差。图 1给出了3组数据估计得到链路时延改正数β的误差,数据3得到β的误差基本上都小于0.1 m,数据1和数据2得到β的误差分别不超过0.25 m和0.15 m。表 5的统计结果说明,随着星间测距精度的提高,链路时延改正数误差的STD和最大值(max)都会降低。链路时延改正数的平均误差(mean)接近于0,说明没有明显的系统误差,也证明了其绝对值是可测的。
| m | |||||
| 链路ID | 卫星PRN | 真值 | 估值 | 误差 | |
| 接收 | 发射 | ||||
| 1 | 01 | 03 | 0.383 | 0.333 | -0.050 |
| 2 | 03 | 01 | 0.572 | 0.469 | -0.104 |
| 3 | 04 | 07 | 0.224 | 0.108 | -0.116 |
| 4 | 06 | 08 | 0.231 | 0.250 | 0.019 |
| 5 | 07 | 16 | 0.078 | 0.136 | 0.058 |
| 6 | 10 | 15 | 0.508 | 0.436 | -0.072 |
| 7 | 16 | 22 | 0.657 | 0.516 | -0.141 |
| 8 | 23 | 08 | -0.042 | 0.072 | 0.114 |

|
| 图 1 3组数据得到的所有链路的时延改正数误差 Fig. 1 Estimation errors of link delay correction obtained from different datasets |
| m | |||
| mean | STD | max | |
| 数据1 | -0.006 | 0.072 | 0.241 |
| 数据2 | -0.007 | 0.044 | 0.130 |
| 数据3 | 0.002 | 0.036 | 0.104 |
因为是仿真数据,笔者重点关注不同方案处理结果的差异。表 6统计了3组数据不同处理方案得到的轨道三维位置误差RMS。方案2较方案1分别降低了84.5%、91.0%和96.1%;方案3较方案1分别降低了83.6%、91.0% 和94.2%;方案4较方案1分别降低了80.6%、91.0%和94.1%。方案3的结果与方案2的结果非常接近,差距不到2%;方案4的结果略逊于方案3。
| m | |||
| 数据1 | 数据2 | 数据3 | |
| 方案1 | 0.742 | 0.803 | 0.825 |
| 方案2 | 0.115 | 0.072 | 0.032 |
| 方案3 | 0.122 | 0.072 | 0.048 |
| 方案4 | 0.144 | 0.072 | 0.049 |
表 7统计了3组数据不同处理方案得到的卫星钟差误差RMS。方案2较方案1分别降低了17.7%、58.5%和84.4%;方案3较方案1分别降低了16.3%、53.7%和74.3%;方案4较方案1分别降低了16.3%、53.7%和74.3%。方案4与方案3结果几乎是一致的,与方案2的差距小于11%。
| m | |||
| 数据1 | 数据2 | 数据3 | |
| 方案1 | 0.203 | 0.123 | 0.109 |
| 方案2 | 0.167 | 0.051 | 0.017 |
| 方案3 | 0.170 | 0.057 | 0.028 |
| 方案4 | 0.170 | 0.057 | 0.028 |
以上结果表明,通过估计设备时延改正数可以显著地提高轨道确定和钟差解算的精度,其效果几乎接近设备时延被准确标定的理想情况。而方案4与方案3相比,尤其是定轨结果,前者的效果要稍差一些。方案4中时延改正数的数量要比方案3多得多,由此造成观测结构减弱是可以理解的。从数据1到数据3,方案2(方案3和方案4)的改进幅度递增,说明星间测距精度越高,定轨和钟差解算结果对设备时延越敏感,估计设备时延参数越显必要。
5 结 论本文从保持与用户算法一致的角度,指出利用星间测距数据求解的卫星钟差也应该包含导航信号设备群时延。建立了联合定轨数据处理的星间测距观测方程,提出通过数据处理估计设备时延改正数是解决设备时延不一致性的有效途径,并给出了估计星间链路设备时延改正数的两种数据处理方法。通过仿真试验验证了所提方法的正确性和有效性。结果表明,采用论文提出的方法可以获得有效的设备时延改正数估值,显著降低设备时延对精密定轨和钟差解算结果的影响。
| [1] | YANG Yuanxi. Review on Progress, Contribution and Challenges of Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39 (1): 1-6. (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6.) |
| [2] | YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813-2819. (杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT 用户的贡献[J]. 科学通报, 2011, 56(21):1734-1740.) |
| [3] | RAJAN J A, BRODIE P, RAWICZ H. Modernizing GPS Autonomous Navigation with Anchor Capability[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland: ION, 2003: 1534-1542. |
| [4] | AMARILLO F F. Inter-satellite Ranging and Inter-satellite Communication Links for Enhancing GNSS Satellite Broadcast Navigation Data[J]. Advances in Space Research, 2011, 47(5): 786-801. |
| [5] | LIN Yiming, HE Shanbao, ZHENG Jinjun, et al. Development Recommendation of Inter-satellites Links in GNSS[J]. Spacecraft Engineering, 2010, 19(6): 1-7. (林益明, 何善宝, 郑晋军, 等. 全球导航星座星间链路技术发展建议[J]. 航天器工程, 2010,19(6): 1-7.) |
| [6] | RAN Chengqi. Implementation of Beidou Navigation Satellite System Programme[C]//Proceedings of CSNC 2011. Shanghai: [s. n.], 2011. (冉承其. 北斗导航卫星系统发展计划的实施[C]//CSNC2011论文集. 上海: [s. n.], 2011: 15-17.) |
| [7] | GENG Tao, LIU Jingnan, ZHAO Qile, et al. Compass Precise Orbit Determination Based on Space-ground Monitoring Network[J]. Geodaetica et Cartographica Sinica, 2011, 40(Sup): 47-51. (耿涛, 刘经南, 赵齐乐, 等. 星地监测网下的北斗导航卫星轨道确定 [J]. 测绘学报, 2011, 40(增刊): 47-51.) |
| [8] | LIU Wanke, GONG Xiaoying, ZHANG Weixing. GPS Orbit Determination with Real Ground Tracking Observations and Simulative Crosslink Ranging Observations[C]//Proceedings of CSNC 2011. Shanghai: [s. n.], 2011: 451-455. (刘万科, 龚晓颖, 张卫星. 联合地面实测数据与星间模拟数据的GPS精密定轨[C]//CSNC2011论文集. 上海: [s. n.], 2011: 451-455.) |
| [9] | CAI Zhiwu, HAN Chunhao, DU Yan, et al. Orbit Determination Method and Accuracy Analysis Utilizing Satellite-ground and Satellite-satellite Links[C]//Proceedings of CSNC 2011. Shanghai: [s. n.], 2011:472-476. (蔡志武, 韩春好, 杜燕, 等. 利用星地和星间链路的轨道测定方法及精度分析 [C]//CSNC2011论文集. 上海: [s. n.], 2011: 472-476.) |
| [10] | SCHAER S. Differential Code Biases(DCB) in GNSS Analysis[R]. IGS Workshop. Miami Beach: IGS, 2008. |
| [11] | HAN Chunhao, LIU Li, ZHAO Jinxian. Conception,Definition and Evaluation of Pseudo-range Measurement[J]. Journal of Astronautics, 2009, 30(6): 2421-2425. (韩春好, 刘利, 赵金贤. 伪距测量的概念、定义与精度评估方法[J]. 宇航学报, 2009, 30(6): 2421-2425.) |
| [12] | Global Positioning System Wing. Navstar GPS Space Segment/ Navigation User Interfaces[R/OL]. 2010-06-12[2012-11-05]. http://www.gps.gov/technical/icwg/#is-gps-200 |
| [13] | LI Xianbin, ZHANG Chuansheng, CHEN Jianyun. Research on the Technology of Calibration of Satellite Constellation Crosslink[C]//China Satellite Navigation Conference(CSNC) 2012 Proceedings. Berlin: Springer, 2012: 423-432. |
| [14] | KLEUSBERG A, TEUNISSEN P J G. GPS for Geodesy[M]. Berlin: Springer, 1996. |
| [15] | PARKINSON B W, SPILKER JR J J. Global Positioning System: Theory and Applications: I[M]. Washington: American Institute of Aeronautics and Astronautics Inc, 1996. |
| [16] | LIN Jinmao, YANG Jun, WANG Yueke, et al. Optimizing Algorithm for the Scheduling of GNSS Crosslink: A Matrix Transform Approach[C]//Proceedings of CSNC 2011. Shanghai: [s. n.], 2011: 467-481. (林金茂, 杨俊, 王跃科, 等. 基于矩阵变换的GNSS星间链路最优规划算法[C]//CSNC2011论文集. 上海: [s.n.], 2011: 467-481.) |
| [17] | SONG Xiaoyong. Study on Orbit Determination of COMPASS Navigation Satellites[D]. Xian: Chang’an University, 2009. (宋小勇. COMPASS导航卫星定轨研究[D]. 西安: 长安大学, 2009). |
| [18] | LIU Wanke. Research and Simulation on Autonomous Orbit Determination and Combined Orbit Determination of Navigation Satellites[D]. Wuhan: Wuhan University, 2008. (刘万科. 导航卫星自主定轨及星地联合定轨的方法和模拟计算[D]. 武汉: 武汉大学, 2008.) |
| [19] | BOCK H, DACH R, JGGI A, et al. High-rate GPS Clock Corrections from CODE: Support of 1Hz Applications[J]. Journal of Geodesy, 2009, 83(11): 1083-1094. |
| [20] | LI Zhendong, HE Shanbao, LIU Chonghua, et al. An Topology Design Method of Navigation Satellite Constellation Intersatellite Links[J]. Spacecraft Engineering, 2011, 20(3): 32-37. (李振东, 何善宝, 刘崇华, 等. 一种导航星座星间链路拓扑设计方法[J]. 航天器工程, 2011, 20(3): 32-37.) |