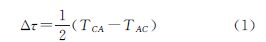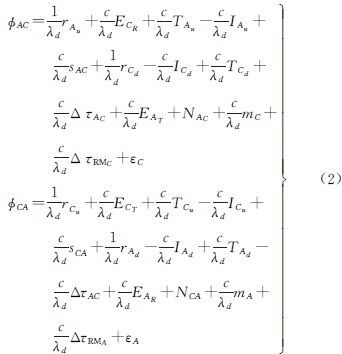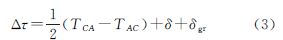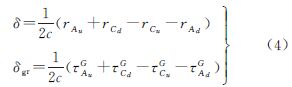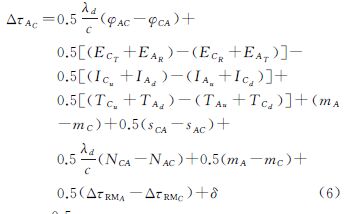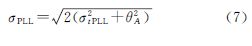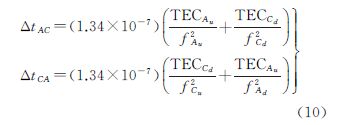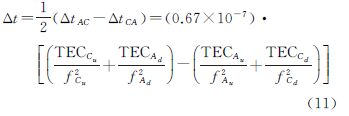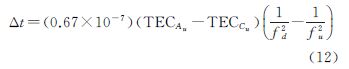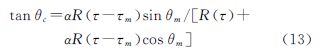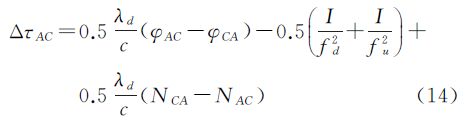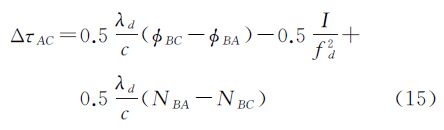2. 中国科学院 精密导航定位与定时技术重点实验室,陕西 西安 710600;
3. 中国科学院大学,北京 100039
2. Key Laboratory for Precise Navigation,Positioning and Timing of the Chinese Academy of Sciences,Xi’an 710600,China;
3. University of Chinese Academy of Sciences,Beijing 100039,China
1 引 言
双向卫星时间频率传递(two-way satellite time and frequency transfer,TWSTFT)方法由于精度高、传输距离远,受到越来越多时间应用及时间体系建设者的重视,是目前公认的时间传递及同步最优的方法[1, 2]。国际计量局(Bureau International des Poids at Mesures,BIPM)也提倡发展TWSTFT系统,以提高国际各时间实验室之间的时间比对精度,根据BIPM的建议,在现有GPS共视法的基础上,在有条件的国家和地区建立全球TWSTFT比对链。截至2010年3月,已有14个国家的17个时间实验室建立了TWSTFT比对链,今后将有更多实验室通过该比对链参与国际原子时(international atomic time,TAI)的计算。因此,TWSTFT将成为最主要的时间比对方法之一[1, 2, 3, 4, 5]。
传统TWSTFT方法采用码伪距作为观测量,受转发器带宽的限制,采用的码速率一般为5 MChip/s,最高为20 MChip/s,从而导致其精度难以进一步提高。而TWSTFT系统采用的载波频率工作在4~14 GHz,是码速率的上百倍,将载波相位应用于TWSTFT系统,理论上可使该系统时间传递精度提高1~2个数量级。
本文提出将载波相位测量应用于TWSTFT系统,分析了实现该方法存在的关键问题,深入研究了载波相位卫星双向时间传递的各种误差,从理论上计算了各误差影响的量值区间,针对每项误差,给出了相应的改正方法。
2 基于载波相位测量的卫星双向时间传递方法采用码伪距作为观测量时,目前国际上通用的卫星双向时间比对公式近似简化为[1, 2]
式中,Δτ为两个进行卫星双向时间传递的地面站之间的钟差;TAC为信号从A站到C站的传输时延; TCA为信号从C站到A站的传输时延。根据码伪距测量原理[1, 2, 3],其精度与码速率大小密切相关,在不考虑其他误差的情况下,卫星双向时间传递若采用的伪码速率为2.5MChip/s,两个码序列码元对齐误差为码元宽度的1/10~1/100,则利用伪码测距的误差为0.5~5ns;若采用的伪码速率为20MChip/s,则利用伪码测距的误差为0.0625~0.625ns。即码速率越高,双向时间传递的精度越高。受到转发器带宽的限制,目前双向时间频率传递系统采用的最高速率为20MChip/s,普通双向多采用5MChip/s。
而TWSTFT系统中采用的载波频率一般在4~12GHz,载波相位测量精度可达0.01~0.05个载波波长,采用4GHz的下行频率信号,精度可达2.5~12.5ps,若采用12GHz的下行频率信号,则精度可达0.83~4.2ps。但在实际应用中,受各种误差的影响,其精度并未达到预期效果[6]。
载波相位卫星双向时间传递方法是在典型TWSTFT系统的基础上,采用载波相位作为观测量,测量载波相位伪距实现卫星双向时间的传递。根据GPS载波相位观测方程,推导载波相位卫星双向时间传递观测方程见式(2)
式中,φAC、φCA分别为C站和A站观测到对方站发射信号的载波相位观测量;ECT、ECR分别为C站发射和接收设备引起的时延;EAT、EAR分别为A站发射和接收设备引起的时延;λd为卫星双向信号下行频率波长;rCu、rAu分别为C站和A站到卫星位置的几何距离;rAd、rCd分别为卫星位置到A站和C站的几何距离;TCu、ICu和TAu、IAu分别为C站和A站上行链路中存在的对流层、电离层延迟;TCd、ICd和TAd、IAd分别为C站和A站下行链路中存在的对流层、电离层延迟;ΔτAC为C站和A站时钟的钟差;sAC为A站发送C站接收过程中卫星转发器带来的时延;sCA为C站发送A站接收过程中卫星转发器带来的时延;NAC、NCA分别为C站和A站接收信号载波相位整周模糊度;mC、mA分别为C站和A站接收信号解算时多径效应引起的时延误差;ΔτRMA为卫星和地面站相对运动引起的A站修正时延;ΔτRMC为卫星和地面站相对运动引起的C站修正时延;εC、εA分别为C站和A站的测量误差。当采用码伪距作为观测量进行卫星双向时间传递时,其精度为纳秒量级,可采用式(1)作为卫星双向时间比对公式。当采用载波相位作为观测量,期望远程比对精度达到10 ps量级时,则不能简单地采用式(1)作为卫星双向比对公式,需要考虑相对论效应等其他误差项。文献[7]在忽略地面站设备时延、卫星转发器时延和大气延迟的情况下,在相对论框架中给出了地心非旋转坐标系精确到0.1ns量级的TWSTFT计算模型
式中,δ 为相对论改正项,δgr为引力时延改正项,分别为 式中,τXyG为相应路径时延的引力时延项(X=A,C; y=u,d)。尽管每条路径引力时延的影响可达几十皮秒,但是改正项δgr引起的影响不会超过1ps,因此在实际计算时,引力时延改正可以忽略。在此基础上,忽略小于1ps量级的误差项,文献[8,9,10]在相对论框架中给出了地心地固系精确到皮秒量级的TWSTFT计算模型本文采用式(5)作为载波相位卫星双向时间传递计算公式,将式(2)中的两式相减,可得
式中,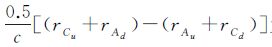 为相对论改正项δ;(φAC-φCA)为两地面站观测量之差; (ECT+EAR)-(ECR+EAT)为两个地面站设备时延差;(ICu+IAd)-(IAu+ICd)为卫星双向路径中电离层时延差;(TCu+TAd)-(TAu+TCd)为卫星双向路径中对流层时延差;(mA-mC)为两个地面站多径效应影响之差; (sCA-sAC)为转发器对卫星双向信号产生的时延之差;(NCA-NAC)为两个地面站的载波相位整周模糊度之差;(rAu+rCd)为地面站A经卫星到地面站C的几何距离;(rCu+rAd)为地面站C经卫星到地面站A的几何距离;(ΔτRMA-ΔτRMC)为两个地面站与卫星的相对运动影响之差。
为相对论改正项δ;(φAC-φCA)为两地面站观测量之差; (ECT+EAR)-(ECR+EAT)为两个地面站设备时延差;(ICu+IAd)-(IAu+ICd)为卫星双向路径中电离层时延差;(TCu+TAd)-(TAu+TCd)为卫星双向路径中对流层时延差;(mA-mC)为两个地面站多径效应影响之差; (sCA-sAC)为转发器对卫星双向信号产生的时延之差;(NCA-NAC)为两个地面站的载波相位整周模糊度之差;(rAu+rCd)为地面站A经卫星到地面站C的几何距离;(rCu+rAd)为地面站C经卫星到地面站A的几何距离;(ΔτRMA-ΔτRMC)为两个地面站与卫星的相对运动影响之差。
根据其工作原理,可以看出将载波相位应用于TWSTFT系统需解决的难点问题主要在于以下几个方面:
首先,载波相位在GPS系统中应用的成功经验不能简单地移植到本系统。因为TWSTFT系统相对于GPS系统多了一条从地面站至卫星的上行链路,且经过卫星转发破坏了载波相位的连续性,解决上行链路和转发器的影响是该系统需要解决的难点之一。
其次,采用载波相位测量存在载波整周模糊度解算及周跳修复问题[11]。TWSTFT系统的整周模糊度解算不同于GPS系统,区别在于:①随着时间推移,GPS系统的观测几何会发生显著变化,而TWSTFT系统采用的卫星为GEO通信卫星,卫星动态小,在短时间内不同历元获得的载波相位观测量变化很小。假定视线方向法向运动幅度最大为100km,星站距离为36000km,引起的视线方向变化角度约为0.16°,不同时刻的观测矩阵非常近似,从而导致观测矩阵呈近似线性相关,需采用正则化方法进行处理[12]。②两个双向观测站采用同一颗卫星,没有冗余观测量。即在短时间内进行TWSTFT的两个观测站,各站只有一个观测量,但存在多个未知数,包括整周模糊度。当TWSTFT系统采用的载波频率在4~12GHz时,一个整周的丢失或者解算误差可达到0.25~0.5ns。因此,载波相位整周模糊度的解算及周跳修复是该系统需要解决的一个难点问题。
同时,由于卫星和地球的相对运动及信号传输时延的存在,双向路径并非完全重合,信号发射、接收及传播过程中存在的误差影响不能完全抵消,存在残差,该残差在码伪距1ns精度要求下作为微小量可被忽略。载波相位测量和码伪距测量被同样的误差源所影响,但影响程度及要求不尽相同。在载波相位更高精度的要求下,各种误差的数据处理要求更加严格,这些残差量如何处理还需进一步分析。本文将对该系统的误差源进行初步的分析。
3 卫星双向载波相位测量误差分析基于载波相位测量的卫星双向时间传递系统的误差源包括信号传播过程中每个环节对载波相位带来的影响,主要为设备误差、空间误差、转发器误差、卫星相对地面站运动引起的误差、整周模糊度解算误差及周跳引起的误差。其中,空间误差包括了电离层、对流层、多径等引起的误差;整周模糊度解算误差及周跳引起的误差在系统需解决难点问题中进行了简要分析,下文主要分析除整周模糊度引起的误差之外的其他误差项。
3.1 设备误差载波相位测量的设备误差主要包含设备绝对时延的标定误差、通道非理想特性引起的载波相位偏移误差及载波相位观测量的测量误差。
设备绝对时延一般通过测量仪器(如矢量网络分析仪、示波器等)进行标定,标定误差受环境、设备寿命等因素影响,且与采用的测量仪器精度相关。因此,本文对该误差未予分析。文献[13]考虑了通道为非理想特性的影响,建立模型对载波相位进行估计,并通过实测验证了所分析模型的有效性,对该误差可参考该文献进行建模消除。本文主要讨论载波相位观测量的测量误差。
地面站接收设备对载波相位测量通过载波锁相环实现,接收设备载波相位测量的误差源主要由相位抖动和动态应力误差组成。卫星双向时间传递时,设备处于静止状态,同时,所采用的地球同步卫星在地心地固系中运动速度很慢,其运动速度小于10m/s,加速度小于5 m/s2。因此在接收设备内部采用二阶环路即可满足跟踪要求。
载波锁相环1σ跟踪测量误差为

式中,σtPLL是由PLL引起的热噪声,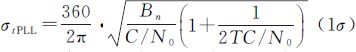 ;Bn为载波环噪声带宽,单位为Hz;C/N0为载噪比,单位为dB-Hz,等于
;Bn为载波环噪声带宽,单位为Hz;C/N0为载噪比,单位为dB-Hz,等于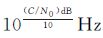 ;T表示预检测积分时间,单位为s。
;T表示预检测积分时间,单位为s。
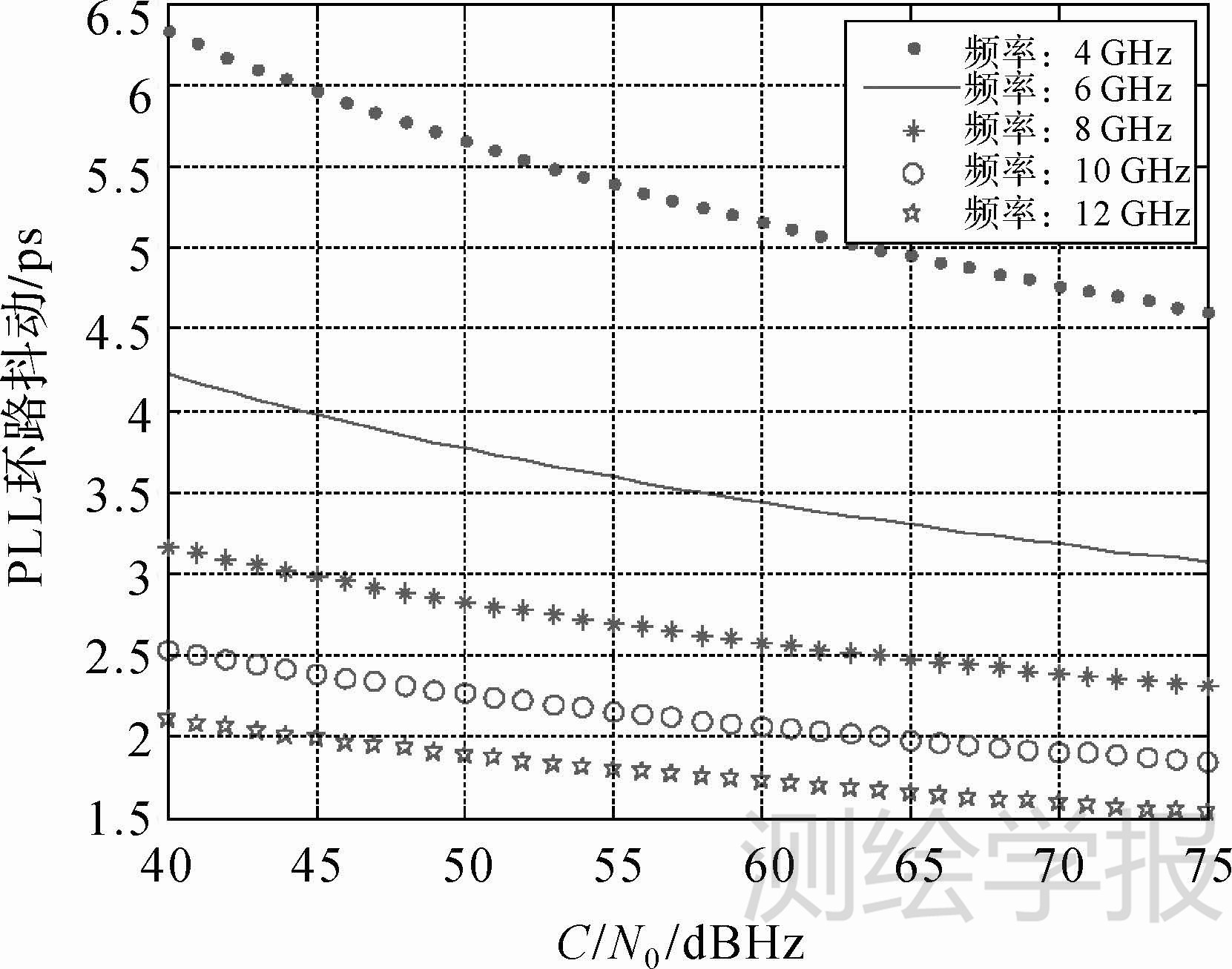
假定C/N0在45~75dB-Hz范围内变化,T为1s,Bn为1Hz,则对于4~12GHz的频率信号PLL环路的抖动如图 1所示。
|
| 图 1 PLL噪声引起的时间偏差 Fig. 1 The time difference caused by PLL noise error |
如图 1所示,当工作频率在4~12GHz变化,取C/N0为55dB-Hz时,σtPLL影响为1.79~5.39ps。
σv是由振动引起的振荡器抖动,由于进行双向的两个地面站都是静止不动的,故取σv=0。
θA是由阿伦方差引起的振荡器抖动,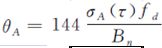 ,单位为度,式中,Bn为载波环噪声带宽,单位为Hz;fd为下行工作频率;σA(τ)为接收设备振荡器的阿伦偏差。
,单位为度,式中,Bn为载波环噪声带宽,单位为Hz;fd为下行工作频率;σA(τ)为接收设备振荡器的阿伦偏差。
该相位抖动带来的时间偏差为
从上述分析可知,该相位抖动引起的时间偏差与fd无关,只与振荡器的阿伦偏差及载波环噪声带宽相关。对于不同的阿伦偏差,在不同的噪声带宽下引起的抖动是不同的,如图 2所示。

|
| 图 2 阿伦偏差引起的时间偏差 Fig. 2 The time difference caused by Allan error |
由图 2可以看出,当环路噪声带宽为1Hz,阿伦方差(1s)分别为1e-11、5e-12、2e-12时,振荡器抖动引起的时间偏差分别为4ps、2ps、0.8ps。对于阿伦方差引起的振荡器抖动,在噪声带宽Bn变得很窄时,阿伦偏差的影响将占据主要地位,因此对于基于载波相位的双向接收设备振荡器的选择上,需要考虑阿伦偏差特性的影响,尽量选择偏差较小的振荡器,减少由此导致的振荡器相位抖动。
θe是环路动态应力误差,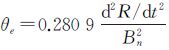 ,单位为度。式中,d2R/dt2表示最大视线方向加速度动态,环路动态应力误差带来的时间偏差为:
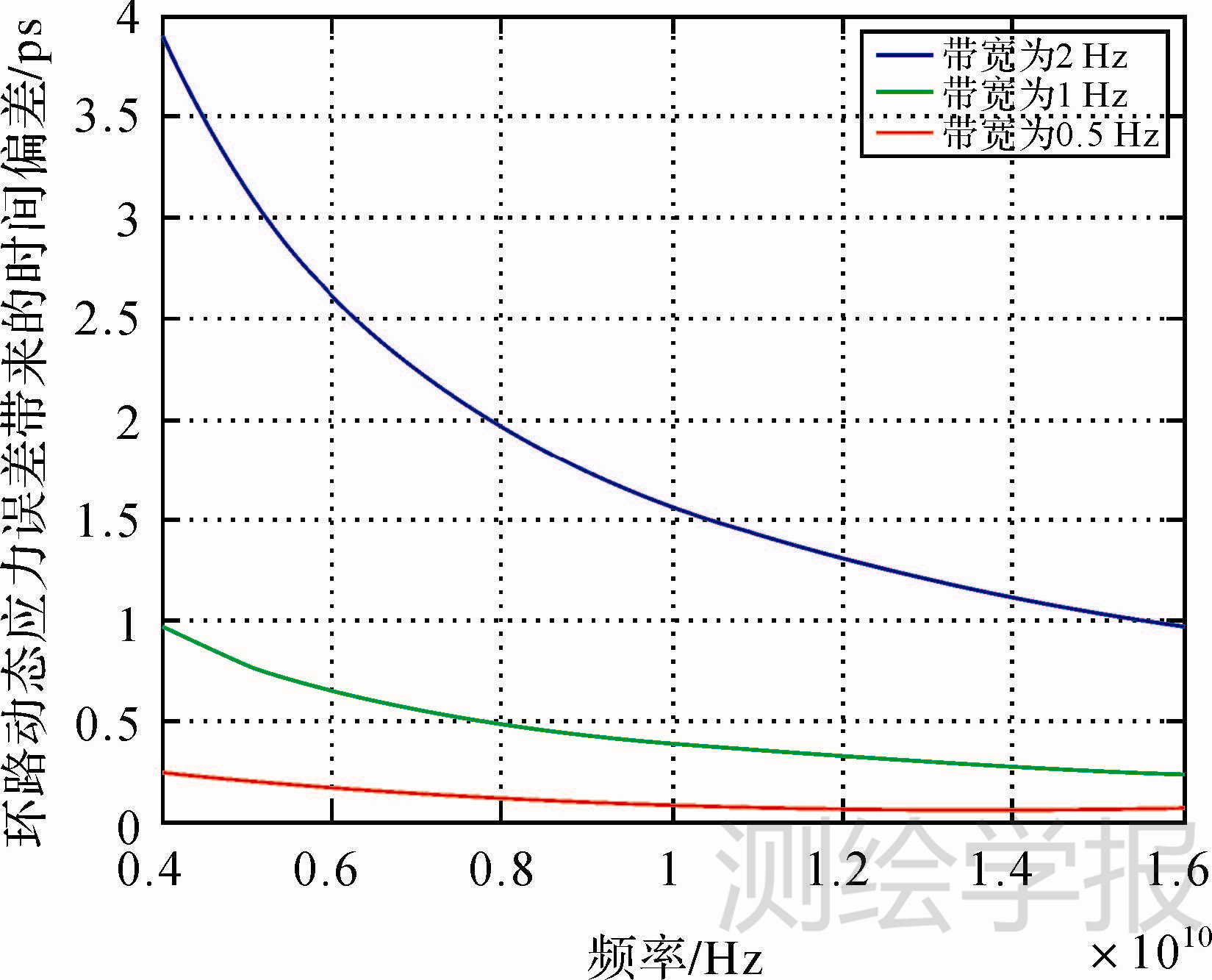
,单位为度。式中,d2R/dt2表示最大视线方向加速度动态,环路动态应力误差带来的时间偏差为: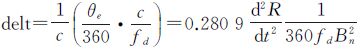 。地球同步卫星在地心地固系中运动速度很慢,其运动速度小于10m/s,假定卫星运动引起的最大视线方向上加速度为5m/s2,用户是静止的,则环路动态应力误差带来的时间偏差如图 3所示。
。地球同步卫星在地心地固系中运动速度很慢,其运动速度小于10m/s,假定卫星运动引起的最大视线方向上加速度为5m/s2,用户是静止的,则环路动态应力误差带来的时间偏差如图 3所示。
|
| 图 3 环路动态应力误差带来的时间偏差 Fig. 3 Time difference caused by the loop dynamic error |
由图 3可以看出,随着频率的不断升高,环路动态应力误差导致的时间偏差越来越小,在环路带宽为1Hz时,4GHz频率信号的环路动态应力误差导致的时间偏差不超过1ps,因此这个量对于精度为15ps的载波相位双向时间频率传递来说,可以忽略。
以上载波相位观测量的各项测量误差均是针对各站进行分析的,在卫星双向时间频率传递系统中,两个站的测量误差与双向路径不相干,不能通过双向路径进行抵消,根据统计学分析,两站的测量误差总和应是以上分析结果的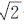 倍。
倍。
通过以上的分析,可得出应用于卫星双向时间传递的σPLL的公式为
3.2 空间误差 3.2.1 电离层误差电离层群时延一阶改正模型可改正电离层总改正的99%。一阶改正量表示为[14]
式中,∫Ndl是为观测方向的电子柱含量,单位为el/m2,可用TEC表示,沿着无线电波路径,TEC值在1016~1019 el/m2;c为光速;f为频率。群时延和载波相位之间的联系用公式简单表示为
式中,负号表示电离层对群时延(码伪距)和载波相位的影响方向相反,即电离层使码伪距观测量延迟,使载波相位观测量提前。即电离层对码观测值和载波相位观测值的影响,就其一阶项而言,数值相同,符号相反。基于上述电离层对载波相位的影响,可得到卫星双向各台站经上、下行路径电离层的载波相位一阶项影响量为
式中,ΔtAC为C站的电离层载波相位改正模型;ΔtCA为A站的电离层载波相位改正模型;fAu、fCu分别为A站和C站的上行频率;fAd、fCd分别为经卫星转发后C站和A站接收到对方站的下行频率;TECAu、TECCu分别为A站和C站到卫星信号传播路径上的总电子含量;TECAd、TECCd卫星到A站和C站信号传播路径上的总电子含量。经过卫星双向传递,依据式(9)、式(10)可知总的电离层时延的影响为
卫星双向时间传递中,大多采用fAu=fCu=fu,fAd=fCd=fd;每一地面站上、下行链路的时间间隔一般小于0.3s,则可认为其上、下行链路信号传播路径的总电子含量相等,即TECAu=TECAd,TECCu=TECCd,则式(11)可写为
文献[16]表明总电子含量在一天中随时间而变化,在不同地区(西安、乌鲁木齐、上海)变化趋势相近,但得到的总电子含量不同。故TECAu和TECCu之间是有差别的,设两站间观测方向的电离层电子柱含量具有70%的相关性,则总的电离层时延在不同工作波段产生的1TECU(1个TEC单元,单位为1016 el/m2)误差如表 1所示。
| 频段 | 上行频率 /GHz | 下行频率 /GHz | 1TECU产生的 误差/ps |
| Ku | 14 | 12 | 0.37 |
| 12 | 10 | 0.62 | |
| 10 | 8 | 1.13 | |
| 8 | 6 | 2.45 | |
| C | 6 | 4 | 6.98 |
当双向时间频率传递系统采用的载波工作频率高于10GHz时,由电离层引起的双向误差小于1.2ps,其影响可以忽略不计,但当载波工作频率低于6GHz时,其影响须采用更高阶的误差模型进行消除。
3.2.2 对流层误差由于对流层气体的折射率n(n>1)比真空的折射系数(n=1)大,使得对流层中的光速小于真空中的光速c。这样在对流层路径长度ds的射线穿越折射系数为n的介质时,会有一个时间延迟dτ=nds/c,等效距离为cdτ=nds,实际总路径延迟S=cτ=∫c·n(s)ds与几何路径距离Sg之间的差值就是附加对流层延迟。
根据文献[14]理想气体的折射率计算公式知道,折射系数与频率无关,相对于频率来讲是恒定的,因此,群速和相速是一样的。其对相位的影响主要表现在对流层附加延迟方面,即式(7)的TAu、TAd、TCu、TCd项。
由于每一地面站上、下行链路的时间间隔一般小于0.3s,可认为地面站气象参数和地固系中的卫星仰角基本不变。因此,经上下路径抵消,对流层时延能够得到很好的消除,它引起的不对称部分一般不再考虑。
3.2.3 多径误差因多路径影响,接收信号分为直接到达和间接到达(物体反射和大气折射)的两类信号。两类信号一起被双向时间频率传递系统的接收天线接收,相互干涉而产生一个复合信号,影响码和相位的量测。由多径引起的载波相位测量误差如式(13)所示
式中,α为多径反射信号相对直达信号的幅度;τm为多径反射信号相对于直达信号的时延;θm为多径反射信号相对于直达信号的相位;R(τ)为扩频码的自相关函数,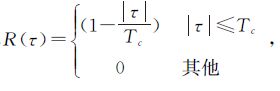 其中,
其中,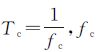 为扩频码速率。图 4给出了当频率为4GHz、8GHz、12GHz、16GHz时,多径信号对载波相位测量的影响,此时假定多径反射信号相对直达信号幅度α=-6dB。从图 4可看出,对于4GHz的传递频率,多径影响可达9ps,当传递频率逐渐升高时,多径影响有所降低,在12GHz时,最大约为2 ps。
为扩频码速率。图 4给出了当频率为4GHz、8GHz、12GHz、16GHz时,多径信号对载波相位测量的影响,此时假定多径反射信号相对直达信号幅度α=-6dB。从图 4可看出,对于4GHz的传递频率,多径影响可达9ps,当传递频率逐渐升高时,多径影响有所降低,在12GHz时,最大约为2 ps。

|
| 图 4 多径效应对载波相位测量的影响 Fig. 4 Multi-path effect influence to carrier-phase measuring |
根据以上分析,对于基于载波相位的双向时间传递来说,多径影响不可忽视,尤其是在选用传递频率较低的L波段、C波段时。
在TWSTFT系统中,空间误差如电离层误差、对流层误差,由于上下行链路的对称,可以认为各项误差的影响具有强相关性,通过上下行链路的差分可有效地消除。而多径因地面站所处的地理位置相差甚远,且各站的多径误差与双向路径无相关性,不能通过双向路径进行抵消。相反,根据统计学分析,进行双向的两个地面站的多径效应误差应是以上分析结果的2倍。对于卫星双向时间频率传递系统和GPS系统的影响是一样的,需根据各站所在环境独立考虑,因此,可参考GPS的抗多径方法[17, 18, 19]
3.3 卫星转发器误差卫星转发器对载波相位测量的影响主要包括收发天线时延、转发通道时延和转发器本地时钟引起的相位变化。
收发天线时延、转发通道时延与采用的具体转发器设备相关,其时延从几纳秒到几百纳秒甚至上千纳秒不等。当卫星收发天线和转发通道对两站的信号完全相同时,卫星转发器对双向时延的影响近似相等,在双向时延计算时,近似认为可完全抵消;当卫星对不同地面站采用不同的收发频率、不同的转发通道和天线波束时,两站的卫星转发器时延不相等,如大西洋上的INTELSAT转发器,这时卫星转发器时延不能在双向时延中被抵消,需要在卫星发射前对双向不同通道的时延或两者时延的差值进行测量,或采用更精确的方法加以测量和标定。
对于载波相位TWSTFT系统,不仅要考虑收发天线时延、转发通道时延的影响,更要考虑转发器本地时钟影响。转发器本地时钟和测站时钟不相干,破坏了载波相位的连续性,且转发器本地时钟的变化量并非恒定常数,而在时间轴上发生波动和漂移,即使卫星对进行双向的测站采用相同的收发频率、相同的信号处理通道,其对载波相位的影响也是不尽相同的。这时需要对星载钟进行建模,对其变化趋势进行预测,以减弱或消除卫星转发器对载波相位测量的影响。
3.4 卫星和地面站相对运动引起的误差 3.4.1 两站到卫星的距离不等引起的误差
通常,进行卫星双向时间传递的两个站到卫星的距离不等,距离差会引起发射信号到卫星的时间差。同时由于卫星的运动,卫星会在不同的位置收到信号,这将使两地面站间的两条比对路径不能完全对称,从而在计算两站间钟差时产生误差。GEO 卫星高度达36 000 km(地心距约为42 000 km),卫星对整个地球张角很小(17.6°)[1]。可以粗略地估计,若两地面站到卫星的距离差约为300 km,钟差计算误差最大约为30 ps,该误差对于载波相位测量的精度要求是不可忽略的。即式(6)中δ项引起的误差需要得到改正。
设计两个比对站时,应尽量使所采用的地球同步卫星处于两比对站中间,如果位置条件不能满足,一般采取调整发射时延方法,对两站位置引起的时延差进行校准,当采用轻微调整发射时延的方法仍不能补偿时,这一影响必须加以改正(Recommendation ITU-RTF,1995—1997)。因为补偿量既可以看作发射时延,又能看作相对钟差,文献[10]给出了将补偿量看作相对钟差、忽略小于1 ps量级的误差项的距离时延改正项的实用计算公式,这里不再赘述。
两地面站钟的不完全同步引起两信号的发射时间不同,对于参加卫星双向时间传递的站,它们事先可以同步到很高的精度(一般小于1μs),因此,仅由两站间钟面时的不同步引起的卫星位置变化约在10-5m ,换算为时间约在10-14 s量级,完全可以忽略。
3.4.3 Sagnac效应误差由于地球和卫星的旋转运动,电波从卫星向地面站传播,或从地面站向卫星传播,若二者经度不同,则存在Sagnac效应。Sagnac效应是一种相对论效应,在卫星双向时间传递系统中,卫星的摄动和地球的自转运动使其信号传播路径发生变化,实际传播路径见文献[8]。
由于实际路径的变化会引起信号传递时延的偏差,可表示为 ,其中,c为光速;ω为地球自转角速度;Ap是卫星、地心和两测站连线构成的多边形在赤道面上投影所围成的面积。
,其中,c为光速;ω为地球自转角速度;Ap是卫星、地心和两测站连线构成的多边形在赤道面上投影所围成的面积。
该偏差可通过上式进行理论计算,该结果对两站的影响大小相等、方向相反,可采用计算结果对偏差进行修正,但由于卫星和地球的运动,所计算的结果存在一定的误差,主要与卫星及地面站的位置精度相关。经分析该计算结果的误差不超过152 ps[8],该误差量级在基于码伪距的测量的双向时间频率传递系统中是可以忽略的,但在基于载波相位测量的卫星双向时间传递系统中,该项误差则远远超出了其理想的精度要求,需采用校准模型对其进行处理。
3.5小 结参考GPS载波相位测量中各种因素的影响,结合卫星双向的实际应用条件,对基于载波相位的卫星双向时间传递存在的误差进行了分析,其量值区间如表 2所示。
| 误差影响因素 | 参考量值/ps | 备注/GHz |
| 设备时延 | 1.96~6.7(不含标校误差) | 12~4 |
| 电离层 | 0.37~6.98 | 12~4 |
| 对流层 | 可忽略 | 可忽略 |
| 多径 | 2~9 | 12~4 |
| 相对运动 | 0~152 | 需采用算法校准 |
分析结果表明,除设备绝对时延标校误差与测量仪器或设备性能相关不能消除外,载波相位观测量的测量误差可通过理论计算结合实地测量得到校准。对流层误差因与频率参量不相干,通过双向路径可得到很好的抵消。卫星和地面站相对运动引起的误差中,两站到卫星的距离不等引起的误差通过采取调整发射时延和理论补偿结合的方法,对两站位置引起的时延差可进行校准,两站钟面时不同步引起的误差量可忽略,因此,该部分主要误差为Sagnac效应引起的误差。而相对论效应、电离层和Sagnac效应引起的误差可采用修正模型进行修正,多径效应对于进行TWSTFT的两个地面站的影响是独立的,各站可分别借鉴GPS载波相位测量的多径消除方法,转发器时延差可在本地建模对其进行测量,忽略双向测量噪声误差,则式(6)可简化为
若在进行卫星双向时间传递的两个地面站分别增加一个接收通道,用于接收地面站自己发射的信号,则该信号可以组成一个自发自收的闭合环路。采用该闭合环路,在发射链路对码和载波的相位进行控制。一方面,可保证在卫星转发器出口处,码和载波相位的一致性;另一方面,可将上行链路的时延进行预偏处理,将地面站发射的信号虚拟到卫星出口[20]时,卫星双向时间传递的两个地面站接收的信号类似于从卫星直接发射的信号(载波和码保持同步),设卫星为B点,则式(14)可改为
此时,TWSTFT系统可借鉴GPS系统整周模糊度解算方法及相关算法。
4 结 论(1) 为进一步提高时间频率传递的精度,结合卫星双向和载波相位两者的优点,将载波相位测量应用于TWSTFT系统是TWSTFT的发展趋势。
(2) 载波相位TWSTFT系统存在以下特点:对流层延迟与频率不相干,因其经过双向路径可得到很好的抵消。电离层延迟与频率成比例关系,经过双向路径后,大部分得到抵消,残差部分与路径的电子浓度差成比例,本文采用一阶修正量对其进行改正后进行TWSTFT的两个系统的研究。整周模糊度解算问题作为载波相位地面站的设备时延和多径效应误差,与双向路径无关,不能相互抵消,该误差的消除方法可参考GPS相关成果。
(3) 载波整周模糊度解算是载波相位卫星双向系统的难点之一,初步提出首先保证转发器出口处码和载波相位的一致,采用伪码结合载波相位的双频整周模糊度解算方法进行解算的思路。
(4) 本文对该系统应用存在的几个难点进行了阐述,对载波相位双向时间频率传递系统的主要误差源进行了分析与初步仿真,给出了各误差影响量级的理论分析结果,得到了基于载波相位测量的卫星双向时间传递简化观测模型。但该模型仅为初步的理论分析结果,其结论还需进一步验证,将载波相位测量应用于卫星双向系统还有大量工作需要作进一步研究。
| [1] | LIU Xiaogang, WU Xiaoping, ZHANG Chuanding. Computational Model and Its Precision Evaluation for Time Comparison by Two-way Satellite Common-view[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(5):415-421.(刘晓刚,吴晓平,张传定.卫星双向共视法时间比对计算模型及其精度评估[J].测绘学报,2009,38(5):415-421.) |
| [2] | KIRCHNER D. Two-way Satellite Time and Frequency Transfer (TWSTFT): Principle, Implementation, and Current Performance[M]. Oxford: Oxford University Press, 1999. |
| [3] | Ll Zhigang, LI Huanxin, ZHANG Hong. Reduction for the Two-way Satellite Time and Frequency Transfer[J]. Acta Astronomica Sinica, 2002, 43(3):422-431. (李志刚,李焕信,张虹.卫星双向法时间比对的归算[J].天文学报, 2002,43(3):422-431.) |
| [4] | JESPERSEN J L, BLAIR B E, GATTERER L E. Characterization and Concepts of Time-frequency Dissemination[J]. IEEE Special Issue on Time and Frequency, 1972,60(5): 502-521. |
| [5] | PIESTER D, BAUCH A. Time Transfer with Nanosecond Accuracy for the Realization of International Atomic Time[J]. Metrologia, 2008, 45(2): 185-198. |
| [6] | SCHEAFER W, PAWLITZKI A, KUHN T. Extension of Two-Way Satellite Time and Frequency Transfer Method to Real-time Operation and Carrier Phase Measurements[C]//Proceedings of the 31st Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting. Beasancon:[s.n.], 1999:203-207. |
| [7] | PETIT G, WOLF P. Relativistic Theory for Picosecond Time Transfer in the Vicinity of the Earth[J]. Chinese Journal of Astronomy and Astrophysics, 1994(11):971-977. |
| [8] | KLIONER S A.The Problem of Clocks Synchronization: A Relativistic Approach[J]. Celestial Mechanics and Dynamical Astronomy, 1992(10): 81-109. |
| [9] | LIU Li, HAN Chunhao. Two Way Satellite Time and Transfer and Its Error Analysis[J]. Processing in Astronomy,2004,22(3):219-226.(刘利,韩春好.卫星双向时间比对及其误差分析[J].天文学进展,2004,22(3):219-226.) |
| [10] | LIU Li. Relativistic Theory of Time Transfer and Techniques of Clock Synchronization[D]. Zhengzhou: Information Engineering University, 2004.(刘利.相对论时间比对理论与高精度时间同步技术[D]. 郑州:信息工程大学,2004.) |
| [11] | BRUYNINX C, DEFRAIGNE P, SLEEWAEGEN J M. Time and Frequency Transfer Using GPS Codes and Carrier Phases: On-site Experiments[J]. GPS Solutions. 1999,3(2): 1-10. |
| [12] | WANG Zhenjie, OU Jikun,LIU Lintao. Investigation on Solutions of Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3):196-201.(王振杰,欧吉坤,柳林涛.单频GPS 快速定位中病态问题的解法研究[J].测绘学报,2005, 34(3):196-201.) |
| [13] | LI Baiyu, LI Caihua, SUN Li, et al. Impact of Non-Ideal Front-End Characteristic on Carrier Phase Ranging Measurement of Navigation Receivers[J]. Journal of Information Engineering University, 2011,12 (1):48-54.(李柏渝,李彩华,孙莉,等.通道非理想特性对导航接收机载波相位测量精度的影响分析[J].信息工程大学学报,2011,12 (1):48-54.) |
| [14] | VAN DIERENDONCK A J. Global Positioning System: Theory and Applications[M]. Washington D C:[s.n.],1996. |
| [15] | LUO Bixian, LUO Jian. Measurement of Group Delay at ns Level Precision in Exterior Ballitic Measurement[J]. Missiles and Space Vehicles, 1995,2:60-70.(罗碧先,罗健.外测转发器ns级精度群时延参数的测试[J].导弹与航天运载技术,1995,2:60-70.) |
| [16] | LI Huiru, LI Zhigang. Determing Ionospheric Delay with Two-way Satellite Dual frequency Observation[J]. Journal of Time and Frequency, 2005, 28(1):29-36. ( 李慧茹,李志刚.通过卫星双向双频观测对电离层时延的测定[J].时间频率学报,2005,28(1):29-36.) |
| [17] | RICHARD D J, VAN N. Method of Estimating a Line of Sight Signal Propagation Time Using a Reduced-Multi-path Correlation Function US:5615232[P].1997-05-25. |
| [18] | YUAN Linguo, HUANG Dingfa, DING Xiaoli,et al. On the Influence of Signal Multipath Effects in GPS Carrier Phase Surveying[J]. Acta Geodaetica et Cartographica Sinica, 2004,33(3):210-215.(袁林果,黄丁发,丁晓利,等,GPS载波相位测量中的信号多路径效应影响研究[J].测绘学报,2004,33(3):210-215.) |
| [19] | DAI Wujiao, DING Xiaoli,ZHU Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(11):321-327.(戴吾蛟,丁晓利,朱建军,等.基于经验模式分解的滤波去噪法及其在GPS 多路径效应中的应用[J].测绘学报,2006,35(11):321-327.) |
| [20] | LI X H, WU H T, BIAN Y J, et al. Satellite Virtual Atomic Clock with Pseudorange Difference Function[J]. Science in China Series G: Physics, Mechanics & Astronomy,2009, 52(3): 353-359. |