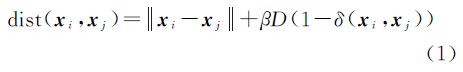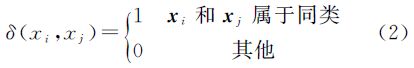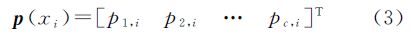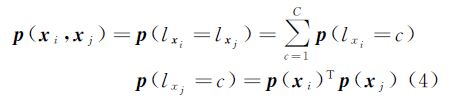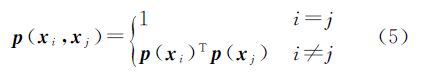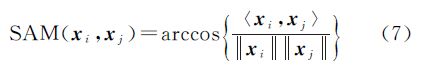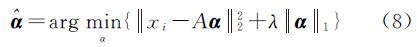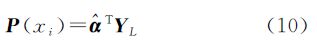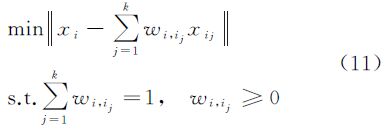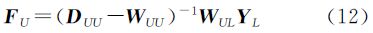高光谱遥感是具有较高光谱分辨率的遥感科学和技术，它具有图谱合一特性，将代表地物性质的光谱和确定地物空间的图像结合在一起，能够获取地球表面丰富的光谱和空间信息，使得在传统多光谱遥感中不可识别的地物在高光谱中能够被识别。因此，高光谱遥感可以获取地物丰富的细节信息，鉴别地物间微小的差别，凭借其对地物属性的准确描述成功应用于地物的精细分类[1]。常用的高光谱分类算法有最大似然分类、神经网络分类、支持向量机等[2, 3, 4, 5, 6]。这些算法都属于有监督分类方法，需要足够数量的标记样本，但是针对高光谱图像获取类别标记数据，是一项耗时耗力、成本高昂的工作[7]。
针对上述问题，许多仅利用少量标记样本的半监督学习方法被提出，主要有Generative Model[8, 9, 10, 11]、Self-training[12, 13, 14]、Co-training[15]、Low Density Separation[16, 17]和基于图的半监督学习方法[18, 19, 20, 21, 22, 23]。在这些方法中，基于图的半监督学习方法与其他方法相比，更加直观、具有良好的分类性能，因此学术界进行了广泛的研究。基于图的半监督方法，首先构造一个图G=〈V,E〉，其中顶点集V由标记样本和未标记样本组成，边E表示样本间的相似性，然后在图中通过成对样本间的相似性，将标记从有标记样本传播到未标记样本。
尽管图的构造是基于图的半监督学习的核心，然而对它的研究并不是很深入[24]。目前传统的数据图构造方法通常包括两个步骤：确定图的邻接结构和计算图上边的权重。大多数基于图的半监督算法都使用k近邻图来确定图的邻接结构，如LP算法[18]、Gaussian Fields and Harmonic Functions[19]和LNP算法[20]。这类方法的不足之处在于，在确定图的邻接结构时，往往根据样本点间的欧氏距离来寻找k近邻点，如果原始欧氏距离相近的两个样本点属于不同的类别，那么很可能有样本点的邻域中包含了来自其他类的邻居点，在这种情况下，很容易造成标签的错误传递。
为了解决上述问题，本文提出一种新的基于属类概率的距离函数，它能够融入样本点的分类信息，相较于欧氏距离，能够有效提高异类样本间的可分性。该距离函数的关键是预测未标记样本的属类概率，笔者采用基于分类的稀疏表达(sparse representation based classification,SRC)[25] 方法来预测未标记样本的属类概率，试验表明，利用SRC算法预估的属类概率向量对原距离函数进行改造后，能有效地扩大异类样本点之间的距离。
本文将基于属类概率的距离函数用于半监督学习线性领域传播算法(linear neighborhood propagation,LNP)和标签传播(label propagation,LP)中，提出基于属类概率的线性邻域传播(class-probability based LNP,PLNP)算法和基于属类概率的标签传播(class-probability based LP,PLP)算法，并将提出的算法应用于高光谱遥感图像分类中。试验结果表明，与LNP算法和LP算法相比，PLNP算法和PLP算法能有效提高高光谱遥感图像的分类精度。
2 类概率距离 2.1 类概率距离的定义
有监督局部线性嵌入(supervised LLE，SLLE)[26]中定义了一种新的距离函数，它融入了类别信息，使得属于不同类别的两个样本间的距离相对大于它们原有的欧氏距离，其具体定义如下
式中，D=maxij||xi-xj||，为所有数据欧氏距离的最大值；β∈[0, 1]是一个可调参数；函数δ(.,.)的定义如下
由此，在新的距离函数下求得的每个训练样本点的邻域中，可包含更多的同类点。然而，它必须以知道样本点的类别信息为前提。事实上，类别信息往往不是全部已知的。同时，很多情况下属类信息是用可能性来表述的。假设数据集初始给定有C类，用pc,i表示xi属于类别c的可能性，构造一个C维的概率(可能性)向量来表示xi的属类情况
通过全概率公式计算两样本点xi和xj属于同类的概率p(xi,xj)
有p(xi,xj)=1，综合式(3)、式(4)，定义
定义距离函数
称式(6)中定义的距离为类概率距离，其中，SAM表示光谱角映射(spectral angle mapper,SAM)，用来替代式(1)中的欧氏距离，这是由于光谱角度量即角度相似系数，比欧氏距离能更好地衡量高光谱图像的光谱特征相似性，SAM定义如下
与SLLE类似，D=maxijSAM(xi,xj)，为所有数据光谱角度量的最大值；β∈[0, 1]是一个可调参数。
2.2 属类概率向量的确定在确定样本点的类概率距离时，需要知道每个样本点的属类概率向量，对于训练样本点，可以轻易地确定它的属类概率向量，但是对于测试样本点，如何给出较为可靠的属类概率向量，是一个非常重要的问题。比较准确的概率向量可以推断出测试点在新的概率空间中的准确位置，从而可以得到准确的分类。笔者采用SRC方法来确定测试样本点的属类概率向量。
假设待分类的对象有c类，并且令A={A1，A2，…，Ac}代表原始的训练样本集，其中Aj表示训练样本集中属于第j类的子样本集。令xi表示测试样本，SRC的流程如下：
(1) 通过求解L1-正则化最小平方问题，对xi在原始训练样本集A上进行稀疏编码
式中，λ为尺度参数；α为测试样本在训练集A上的投射系数向量；得到的解是一个稀疏向量，即只有少数元素不为零。
(2) 通过式(9)对xi分类
式中，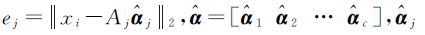
是与第j类训练样本相关的系数向量。
从SRC方法可以得出，测试样本点可完全或近似地由非常少的一组样本的线性组合表示，当有训练样本点所对应的分解系数为非零时，这个训练样本点很可能与待测试样本点属于同一类。针对SRC能从信号的稀疏性角度获得更有价值的信息，并能在高维空间对信号的类别具有很好的判断的特点，本文提出利用SRC方法来确定测试样本的属类概率向量，其算法步骤如下：
(1) 确定训练样本的初始标记矩阵YL∈l×c，如果样本xi的标记为yi=j，则yij=1，否则yij=0。
(2) 采用式(8)求稀疏向量â。
(3) 根据式(10)求出每个样本点的属类概率向量
对概率向量归一化，则有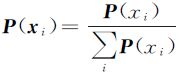
。
第2节提出的基于属类概率的距离函数，由于其融入了样本点的分类信息，相较于欧氏距离，能够有效地提高样本间的可分性。为此，将该距离函数用于半监督学习LNP和LP算法中，提出PLNP和PLP算法。PLNP算法和PLP算法都是采用类概率距离确定图的邻接结构，它们只是在权值计算方式上有所不同，PLNP采用的权值计算方式是基于局部线性嵌入LLE的非负权重，而PLP采用高斯函数计算权值。
3.1 PLNP算法给定数据集X={x1,x2,…,xn}和相应的标记集为C={1,2，…,c}，其中，xi∈Rd，前l个样本点xi∈X(i≤l)为有标记样本，其标记为{y1,y2,…,yl}∈C，其余的样本点xu∈X(l+1≤u≤n)为未标记样本。PLNP算法的目的就是预测未标记样本xu的标记。
令P表示n×c非负矩阵，F=[F1F2…Fn]T∈P代表一种对数据集X的分类结果，每个样本点xi的标记为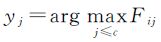
。定义Y∈P为初始标记矩阵，如果xi的标记为yi=j，则yij=1，否则yij=0；对于无标记样本，其对应的yij全为0。将F和Y化为分块矩阵F=
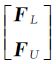，Y=
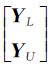，其中，FL和YL为与标记样本点相关的矩阵；FU和YU是与未标记样本点相关的矩阵。在此，限制FL=YL。
PLNP算法步骤如下：
(1) 对每个样本点xi，根据式(6)定义的类概率距离寻找它的k个最近邻点集{xi1,xi2,…,xik}。
(2) 通过求解下述优化问题，计算局部线性组合权值Wij
(3) 求对角矩阵D，其中，Dii=
，并将权值矩阵W和对角矩阵D从l行、l列之后分4块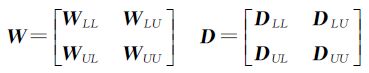
(4) 通过文献[12]的标签传递公式，求未标记样本的预测结果
(5) 根据步骤(4)求得的FU,给出每个样本点xi的类别标签yj=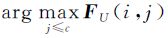
。
在3.1小节中给出了将概率向量融入距离关系来确定图的邻接结构的PLNP算法，该算法在计算权重这一环节利用了基于LLE的权重计算方式，如果换作半监督学习中其他的权重计算方式依然是可行的。
LP算法是一种利用高斯核函数来计算样本间相似性关系的半监督学习算法，本文将类概率距离用于LP算法中，提出PLP算法，其算法步骤如下：
(1) 对每个样本点xi，根据式(6)定义的类概率距离寻找它的k个最近邻点集{xi1,xi2,…,xik}。
(2) 求高斯核权值Wij
(3) 接下来的步骤与PLNP算法的(3)、(4)、(5)步相同。
4 试验结果与分析为了对本文算法的分类效果进行评估，在6组高光谱遥感图像数据集上进行了试验验证。首先对本文提出的PLNP算法、PLP算法与LP、LNP算法进行了试验比较，然后对类概率距离的有效性及复杂度进行了分析。
4.1 数据描述本试验采用两个不同高光谱传感器所获取的高光谱图像。一个是由美国国家航空航天局(NASA)的EO-1卫星上的Hyperion 设备获取，另两个是由可见光红外成像光谱仪(AVIRIS)获取。Hyperion获取的242波段数据具有10 nm的光谱分辨率和30 m×30 m的空间分辨率，其光谱范围是357～2576 nm，去除未校准波段、噪声波段以及光谱重叠波段，剩余145个波段。本试验采用的Hyperion数据采集于Okavango Delta、Botswana(BOT)地区。在美国肯尼迪航天中心由AVIRIS拍摄224波段的高光谱图像(KSC)，其光谱范围是400～2500 nm，光谱分辨率为10 nm，空间分辨率为18 m×18 m。去除噪声和水汽吸收波段，剩余176波段进行分类试验。另外一个AVIRIS数据(Indian Pine)是1992年于美国印地安那州的一个农场拍摄的，其空间分辨率是20 m×20 m。去除水汽吸收波段，剩余200波段。这3种图像所包含的标记类别名称以及数目如表 1所示,其中BOT数据包括9个地物类别；KSC数据包括13个地物类别；Indian Pine数据包括16个地物类别，英文为各类别名称，括号内的数字为对应类别的样本数目。
| BOT | KSC | Indian Pine |
| 标号 | 类别名称 | 标号 | 类别名称 | 标号 | 类别名称 |
| 1 | Water (158) | 1 | Scrub (761) | 1 | Alfalfa (54) |
| 2 | Floodplain (228) | 2 | Willow swamp (243) | 2 | Corn-No till (1434) |
| 3 | Riparian (237) | 3 | Cabbage palm hammock (256) | 3 | Corn-Min till (834) |
| 4 | Firescar (178) | 4 | Cabbage palm/oak(252) | 4 | Corn (234) |
| 5 | Island Interior (183) | 5 | Slash pine (161) | 5 | Grass/pasture (497) |
| 6 | Woodlands (199) | 6 | Oak/broadleaf hammock (229) | 6 | Grass/trees (747) |
| 7 | Savanna (162) | 7 | Hardwood swamp (105) | 7 | Grass/pasture-mowed (26) |
| 8 | Short Mopane (124) | 8 | Graminoid marsh (431) | 8 | Hay-windrowed (489) |
| 9 | Exposed Soils (111) | 9 | Spartina marsh (520) | 9 | Oats (20) |
| 10 | Cattail marsh (404) | 10 | Soy-No till (968) | ||
| 11 | Salt marsh (419) | 11 | Soy-Min till (2468) | ||
| 12 | Mud flats (503) | 12 | Soy-clean (614) | ||
| 13 | Water (927) | 13 | Wheat (212) | ||
| 14 | Woods (1294) | ||||
| 15 | Bldg-grass-trees-drives (380) | ||||
| 16 | Stone-steel towers (95) |
本试验采用这3个高光谱图像的6个数据集进行分类试验。BOT地区包括湿地和高地两个生态系统，其标记数据包括9个类别，其中类别3(riparian)和类别6(woodlands)的光谱非常相似，是最难进行区分的两个类别。试验中，笔者采用这两个类别(C3,C6)和全部9个类别(C1—C9)数据进行分类试验。KSC数据中，试验采用类别(C3,C6)和全部13个类别(C1—C13)数据进行分类试验。Indian Pine数据中，选择最难区分的两类(类别3：Corn-min tillage，C3类别12：Soybeans-high tillage,C12)和所有的16个类别(C1—C16)进行试验。
4.2 PLP、PLNP与LP、LNP算法的比较笔者将提出的PLNP算法和LNP算法与LNP算法和LP算法在上述6组高光谱图像数据集上进行试验比较。试验采用总分类精度(overall accuracy,OA)作为评价标准[27]。对6组试验数据集，笔者从每类样本中分别选取3、5、10、15、20的样本点作为训练样本点，其余的作为测试样本集，对试验的数据集进行了归一化处理。同时，为了比较的公正性，对每个数据集在给定的不同的标记样本下，随机产生10次有标记数据和未标记数据的划分，并取这10次划分上的平均分类率作为最终的结果。
对于半监督算法，由于标记数据较少，参数的选择是根据LOO(leave-one-out)[28]的方法来实现，它的基本思想是：假设有L个标记数据，每1次将1个标记数据xi拿到未标记数据中，用剩下的L-1个标记数据对xi分类(利用LP和LNP算法)，则L个标记数据就有L个分类结果，可以计算分类算法在L个数据上的OA。在不同参数下进行该试验，最大OA就对应最优参数。
图 1—图 6分别列出上述4个算法在6个数据集上的分类结果，横坐标表示每类样本的标记个数，纵坐标表示10次的平均分类正确率。
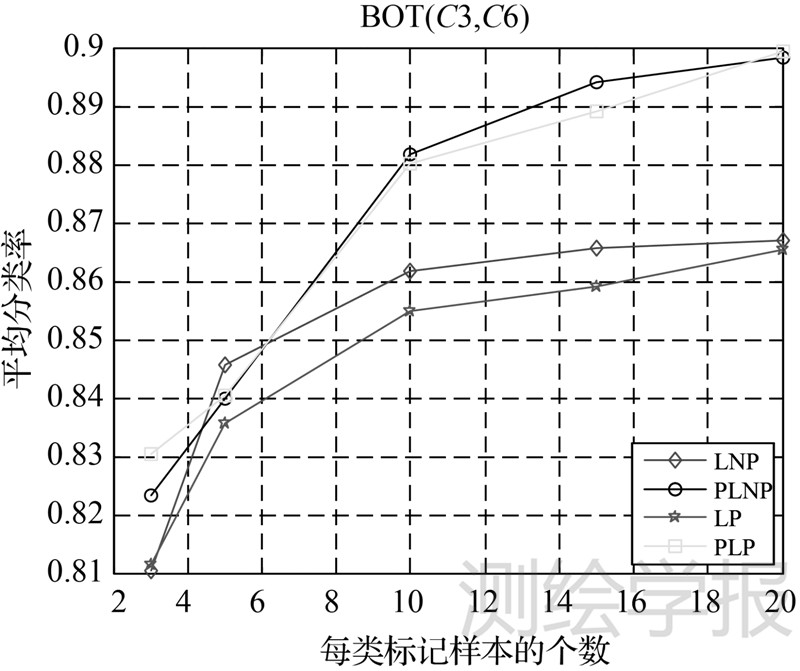
(1) 图 1表示4种算法在BOT数据(C3,C6)两类的分类结果。从中可以看出，PLNP算法只有在每类样本的标记个数为5个时的分类率略低于LNP算法，其他情况下都较LNP算法有1%～3%的提高。PLP算法在所有标记率下都高于LP算法。
|
| 图 1 4种算法在BOT(C3,C6)的分类结果 Fig. 1 Results of four algorithms on classes 3 and classes 6 in BOT data |
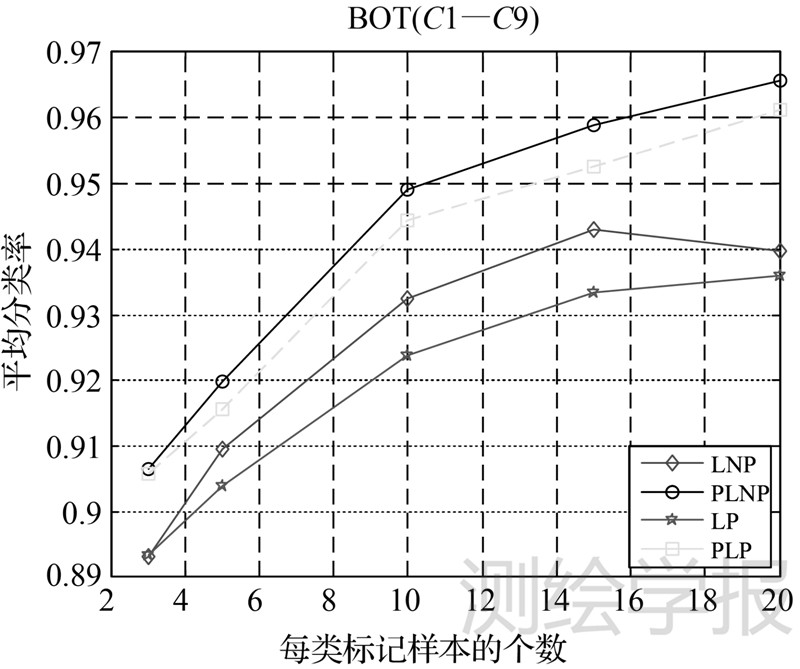
(2) 图 2表示4种算法在BOT数据(C1—C9)全类的分类结果。从中可以看出，PLNP和PLP算法在所有标记率下的分类率都高于LNP和LP 算法。
|
| 图 2 4种算法在BOT(C1—C9)的分类结果 Fig. 2 Results of four algorithms on all classes in BOT data |
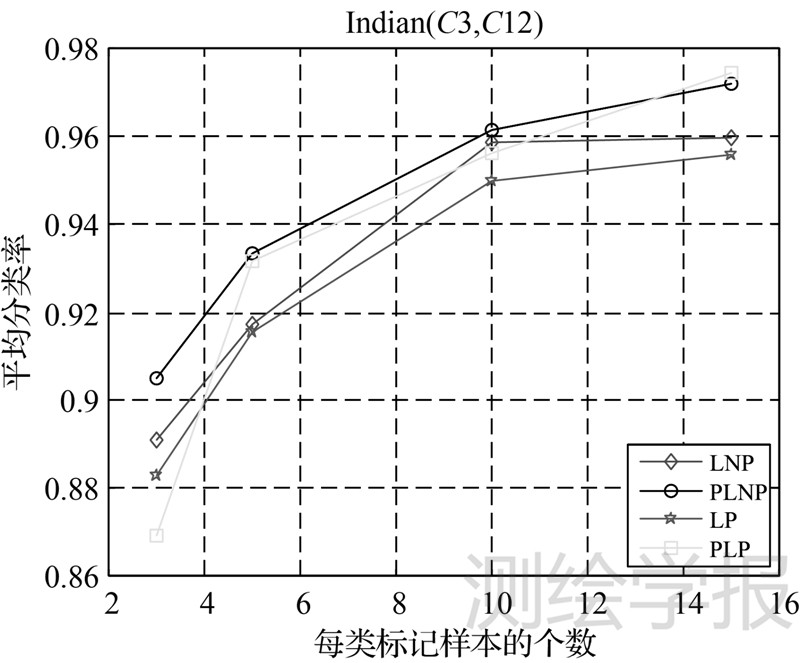
(3) 图 3表示4种算法在Indian Pine数据(C3,C12)两类的分类结果。从中可以看出，PLNP算法的分类率较LNP算法有1%～2%的提高，而PLP算法只有在标记个数为3时的分类率低于LP算法，在其他标记率下都高于LP算法。
|
| 图 3 4种算法在Indian(C3,C12)的分类结果 Fig. 3 Results of four algorithms on classes 3 and classes 12 in Indian data |
(4) 图 4表示4种算法在Indian Pine数据C1—C16全类的分类结果。从中可以看出，PLNP算法的分类率较LNP算法有5%～12%的提高，而PLP算法的分类率较LP算法有7%～13%的提高。
|
| 图 4 4种算法在Indian(C1—C16)的分类结果 Fig. 4 Results of four algorithms on all classes in Indian data |
(5) 图 5表示4种算法在KSC数据(C3,C6)两类的分类结果。从中可以看出，PLNP算法的分类率较LNP算法有2%左右的提高，而PLP算法的分类率较LP算法有3%～4%的提高。
|
| 图 5 4种算法在KSC(C3,C12)的分类结果 Fig. 5 Results of four algorithms on classes 3 and classes 12 in KSC data |
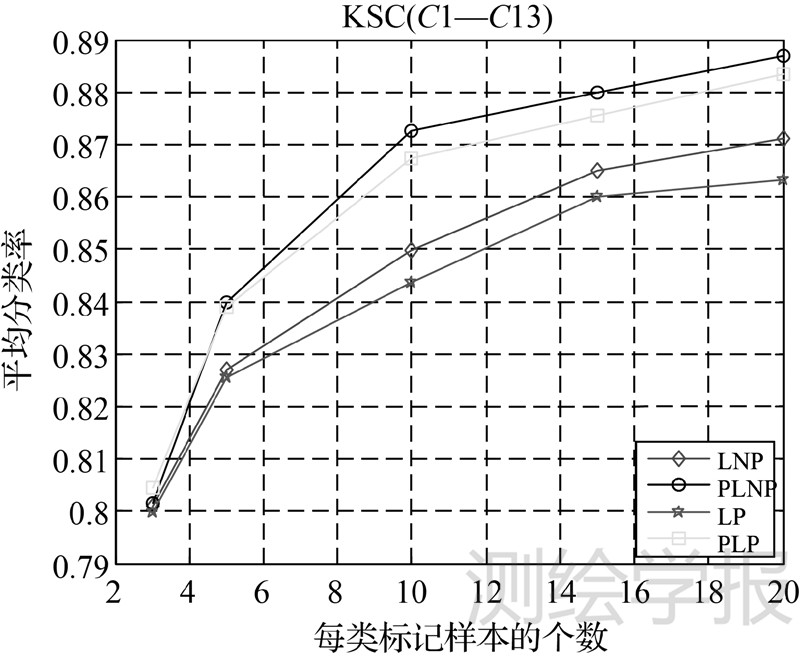
(6) 图 6表示4种算法在KSC数据(C1—C13)全类的分类结果，从中可以看出，PLNP算法的分类率较LNP算法有1%～3%的提高，而PLP算法的分类率较LP算法有1%～2%的提高。
|
| 图 6 4种算法在KSC(C1—C13)的分类结果 Fig. 6 Results of four algorithms on all classes in KSC data |
(7) 从图 1—图 6中可以看出，由于PLNP的权值计算方式要优于PLP的，在大多数情况下，PLNP比PLP取得了更好的分类效果。
分析这4个数据集的结果，可以得到：①在大多数情况下，PLNP和PLP可以比LNP和LP取得更好的分类效果，在样本点数很少的情况下可能存在例外，这是由于SRC是一种有监督分类算法，会受到样本点数量的影响，所以在标记样本个数非常少的情况下，某些未标记数据的属类概率可能存在误差，使得全部数据中的近邻选择效果受到影响。②在Indian Pine数据(C1—C16)全类数据的分类试验中，PLNP和PLP算法对比原来传统的半监督算法在分类率上有较大的提高。
上述试验结果表明，相比于传统的光谱角度量，本文提出的基于概率的距离函数是一个更好的度量函数，根据此距离函数构图的半监督学习能有效地提高高光谱图像分类的效果。
4.3 类概率距离的有效性及复杂度分析首先，笔者利用K近邻(K nearest neighborhood,KNN)算法来验证改造后的类概率距离是否能有效地扩大异类样本点间距离。 KNN算法的思路是，根据某一距离度量函数求待测样本的K个近邻，然后通过表决的方式，即依据这K个近邻中属于某一类的样本数最多来对待测样本进行判决。在K值确定的情况下，KNN算法完全取决于距离度量方式，因此，分别用光谱角距离和类概率距离求近邻，并选用BOT和Indian Pine高光谱数据进行分类试验。在此，令K=5，试验结果如表 2、表 3所示(在K等于其他值时也得出了同样的结果，这里只列出了K=5的分类结果)。
| 图像数据 | BOT(C3,C6) | BOT(C1—C9) | |||||||||
| 每类标记数据个数 | 3 | 5 | 10 | 15 | 20 | 3 | 5 | 10 | 15 | 20 | |
| 基于光谱角距离的KNN/(%) | 71.30 | 75.66 | 81.76 | 82.54 | 83.89 | 71.33 | 80.10 | 86.14 | 89.47 | 91.06 | |
| 基于类概率距离的KNN/(%) | 75.19 | 79.86 | 86.76 | 87.44 | 89.65 | 79.50 | 86.76 | 91.94 | 94.58 | 95.33 | |
| 图像数据 | Indian(C3,C12) | Indian(C1—C16) | |||||||
| 每类标记数据个数 | 3 | 5 | 10 | 15 | 3 | 5 | 10 | 15 | |
| 基于光谱角距离的KNN/(%) | 54.90 | 65.29 | 71.96 | 79.84 | 44.91 | 53.83 | 61.64 | 66.51 | |
| 基于类概率距离的KNN/(%) | 56.13 | 73.17 | 80.06 | 89.36 | 56.68 | 65.16 | 72.58 | 78.13 | |
如表 2、表 3所示，对于BOT和Indian Pine这两个高光谱数据集，基于本文提出的类概率距离的KNN算法的分类正确率都要优于基于光谱角距离的KNN算法，表明在类概率距离函数的度量下，每个样本点的邻域中可包含更多同类的样本点。
然后，为直观比较两种距离计算方式花费的代价，使用运算时间作为计算复杂度的度量。试验软件环境：Matlab 2011b、Windows XP。硬件环境：CPU AMD Athlon(tm) X2 Dual 2.00 GHz/1 GB RAM。表 4为在选取的4个数据集上两种距离计算方式的运行时间。从表中可以看出，类概率距离的计算时间多于光谱角距离，但仍是可以接受的。并且由于根据类概率距离构图的半监督学习的分类效果要明显优于基于光谱角距离构图的半监督学习，所以本文算法具有较好的实用性。
| s | ||
| 数据集 | 光谱角距离 | 类概率距离 |
| BOT(C3,C6) | 0.036 78 | 1.076 9 |
| BOT(C1—C9) | 0.391 1 | 10.134 2 |
| Indian(C3,C12) | 0.061 4 | 1.360 4 |
| Indian(C1—C16) | 1.148 7 | 37.388 |
传统的基于图的半监督高光谱图像分类在确定图的邻接结构时，光谱角距离往往不能很好地挖掘样本点间的相似性关系。针对此类问题，本文提出用基于分类的稀疏表达来预估未标记样本的属类概率向量，然后利用这个概率向量对原来的距离函数进行改进，在新的距离函数的度量下，每个样本点的邻域中，可包含更多的同类样本点，根据这个新的距离函数，笔者提出基于属类概率距离构图的半监督学习方法。在高光谱图像数据集上的分类试验结果表明，本文提出的算法在性能上总体优于传统的基于图的半监督学习算法，总分类精度上有了明显的提高。本文的研究工作还存在有待改进的地方，例如，如何采用更有效的权值计算方式来获得更好的分类效果，进一步研究快速算法从而降低运行时间等问题。
| [1] | MA Li. Manifold Learning Methods for Hyperspectral Image Classification and Anomaly Detection [D].Wuhan:Huazhong University of Science & Technology,2010.(马丽. 基于流形学习算法的高光谱图像分类和异常检测 [D].武汉:华中科技大学,2010.) |
| [2] | RICHARDS J A, JIA X. Using Suitable Neighbors to Augment the Training Set in Hyperspectral Maximum Likelihood Classification[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 774-777. |
| [3] | PLAZA J, PLAZA A, PEREZ R, et al. Paralled Classification of Hyperspectral Images Using Neural Networks[J]. Computational Intelligence for Remote Sensing, 2008, 133: 193-216. |
| [4] | MOUNTRAKIS G, IM J, OGOLE C. Support Vector Machines in Remote Sensing: A Review[J].ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(3): 247-259. |
| [5] | YANG Guopeng, YU Xuchu, ZHOU Xin, et al. Research on Relevance Vector Machine for Hyperspectral Imagery Classification[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6):572-578.(杨国鹏, 余旭初, 周欣,等. 基于相关向量机的高光谱影像分类研究[J]. 测绘学报, 2010, 39(6):572-578.) |
| [6] | TAN Kun, DU Peijun. Wavelet Support Vector Machines Based on Reproducing Kernel Hilbert Space for Hyperspectral Remote Sensing Image Classification[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(2):142-147.(谭琨, 杜培军. 基于再生核Hilbert空间小波核函数支持向量机的高光谱遥感影像分类[J]. 测绘学报, 2011, 40(2):142-147.) |
| [7] | KIM W,CRAWFORD M M. Adaptive Classification for Hyperspectral Image Data Using Manifold Regularization Kernel Machines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(11): 4110-4121. |
| [8] | MILLER D J, UYAR H S. A Mixture of Experts Classifier with Learning Based on Both Labeled and Unlabelled Data[C]//Advances in Neural Information Processing Systems 9. Cambridge:MIT Press. 1997:571-577. |
| [9] | NIGAM K, MCCALLUM A K, THRUM S,et al. Text Classification from Labeled and Unlabeled Documents Using EM[J]. Machine Learning, 2000,39(2-3):103-134. |
| [10] | RATSABY J, VENKATESH S. Learning from a Mixture of Labeled and Unlabeled Examples with Parametric Side Information[C]//Proceedings of the Eighth Annual Confer-ence on Computational Learning Theory. New York: [s.n.], 1995: 412-417. |
| [11] | CASTELLI V, COVER T. The Exponential Value of Labeled Samples[J]. Pattern Recognition Letters,1995,16 (1):105-111. |
| [12] | YAROWSKY D. Unsupervised Word Sense Disambiguation Rivaling Supervised Methods[C]//Proceedings of the 33rd annual meeting of the Association of Computational Linguistics. Cambridge:[s.n.],1995:189-196. |
| [13] | RILOFF E, WIEBE J, WILSON T. Learning Subjective Nouns Using Extraction Pattern Bootstrapping[C]//Proceedings of the 7th Conference on Natural Language Learning. Reykjavik:[s.n.],2003. |
| [14] | ROSENBERG C, HEBERT M, SCHNEIDERMAN H. Semi-supervised Self-training of Object Detection Models[C]//Proceedings of the 7th IEEE Workshop on Applications of Computer Vision.Washington DC:[s.n.],2005. |
| [15] | BLUM A, MITCHELL T. Combining Labeled and Unlabeled Data with Co-training[C]//Proceedings of the 11th Annual Conference on Learning Theory. Madison:[s.n.]. 1998:92-100. |
| [16] | CHAPELLE O, ZIEN A. Semi-supervised Classification by Low Density Separation[C]//Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics.Illinois:[s.n.],2005:57-64. |
| [17] | JOACHIMS T. Transductive Inference for Text Classification Using Support Vector Machines[C]//Proceedings of the 16th International Conference on Machine Learning. Bled:[s.n.],1999:200-209. |
| [18] | ZHU X J, LAFFERTY J, GHAHRAMANI Z. Semi-supervised Learning Using Gaussian Fields and Harmonic Functions[C]//Proceedings of the 20th International Conference on Machine Learning. Menlo Park:[s.n.],2003: 912-919. |
| [19] | ZHOU D Y, BOUSQUET O, LAL T, et al. Learning with Local and Global Consistency[C]//Advances in Neural Information Processing Systems 16. Massachusetts:[s.n.],2004,16: 321-328. |
| [20] | WANG F, ZHANG C S. Label Propagation through Linear Neighborhoods[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(1): 55-67. |
| [21] | ZHAO Yinghai, CAI Junjie, WU Xiuqing, et al. Sparse Graph Based Transductive Multi-label Learning for Video Concept Detection[J]. Jounal of Pattern Recognition & Artificial Intelligence, 2011, 24(6): 825-831. (赵英海, 蔡俊杰, 吴秀清, 等. 基于稀疏化图结构的转导多标注视频概念检测算法[J]. 模式识别与人工智能, 2011, 24(6):825-831.) |
| [22] | ROHBAN M H , RABIEE H R.Supervised Neighborhood Graph Construction for Semi-supervised Classification[J]. Pattern Recognition Letters, 2012, 45(4):1363-1372. |
| [23] | KOBAYASHI T, WATANABE K , OTSU N. Logistic Label Propagation[J]. Pattern Recognition Letters, 2012, 33(5):580-588. |
| [24] | ZHU X J, GOLDBERG A B. Introduction to Semi-supervised Learning [M]. USA:Morgan & Claypool, 2009. |
| [25] | WRIGHT J, YANG A Y, GANESH A, et al. Robust Face Recognition via Sparse Representation[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2009, 312(2):210-227. |
| [26] | RIDDER D D, KOUROPTEVA O, OKUN O, et al. Supervised Locally Linear Embedding[J]. Lecture Notes in Computer Science, 2003: 333-341. |
| [27] | GAO Hengzhen. Research on Classification Technique for Hyperspectral Remote Sensing Imagery[D].Changsha:National University of Defense Technology, 2011.(高恒振. 高光谱遥感图像分类技术研究[D].长沙:国防科学技术大学,2011.) |
| [28] | WU M, SCHOLKOPF B. Transductive Classification via Local Learning Regularization [C]//Proceedings of the 11th International Conference on Artificial Intelligence and Statistics.Sanjuan:[s.n.],2007:1529-1536. |