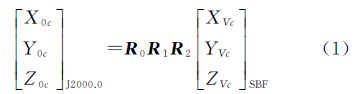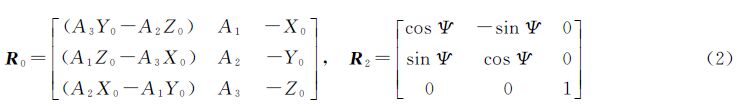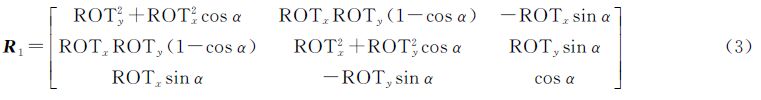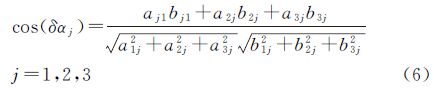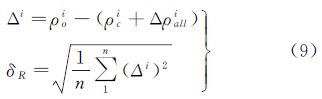2. 中国地震局地质研究所 地震动力学国家重点实验室,北京 100029;
3. 中国测绘科学研究院 大地测量与地球动力学研究所,北京 100039;
4. 中国科学院 国家授时中心,陕西 西安 710600;
5. 东华理工大学 测绘工程学院,江西 南昌 344000
2. State Key Laboratory of Earthquake Dynamics,Institute of Geology,CEA,Beijing 100029,China;
3. Institute of Geodesy and Geodynamics,Chinese Academy of Surveying and Mapping,Beijing 100039,China;
4. National Time Service Center,Chinese Academy of Sciences,Xi’an 710600,China;
25. Faculty of Geomatics,East China Institutes of Technology,Nanchang 344000,China
1 引 言
继Topex/Poseidon(T/P)和Jason-1卫星之后,美国宇航局(NASA)和欧洲气象卫星组织(EUMETSAT)于2008年6月20日又将一颗海洋测高卫星Jason-2送入太空[1]。该卫星将协同在同一环地球轨道上运行的Jason-1卫星,继续对全球海平面进行高精度监测,负责向地面传输全球海平面高度、洋流流速及方向、海洋内储存的热量等数据。这些数据将有助于提高飓风预测准确度,并更准确地为船舶提供海事气象预报[1, 2]。
文献[2, 3]提出了海洋测高计划,通过载有高度计的卫星来进行海洋科学研究,这些海洋卫星数据的有效应用取决于海洋卫星本身的定轨精度,尤其是径向精度。针对Jason-2海洋卫星而言,为了协同Jason-1卫星的科学任务,要求Jason-2卫星的轨道精度至少在径向分量上应与Jason-1卫星一致。因此,Jason-2卫星除在轨道设计方面仍沿袭Jason-1卫星外,选择了较高的轨道(约1335 km)以减小定轨时地球引力场和大气阻力的影响;除此之外,同样采用了卫星激光测距(satellite laser ranging,SLR),天线电定位(doppler orbitography and radiopositioning integrated by satellite,DORIS)和GPS多项定轨技术[1, 3]。
Jason-2卫星同时搭载了GPS、SLR和DORIS 3种定轨手段,如何基于不同手段确定高精度的卫星轨道是卫星定轨策略重要的研究内容,它涉及数据的质量控制、先验力学模型、测量模型及参数的最优估计和约束等问题[3, 4]。文献[5, 6]曾讨论GPS、SLR和DORIS 3种手段的定轨策略,然而,这些定轨策略是针对先前的卫星而言。目前,Jason-2卫星的测量设备相对于先前一代设备从测量精度和可靠性方面均有了提高,此外,随着对卫星的空间受力和测量模型认识逐渐深化,定轨的测量模型和力学模型均有了较大的改变[1, 7, 8],因此,研究目前Jason-2卫星精密定轨策略具有重要的现实意义。卫星姿态模型误差的轨道影响是卫星精密定轨中的另外一个重要问题,因为在卫星精密定轨中,难以精确模拟实际姿态,实测姿态数据存在时延性和不稳定性问题[1, 2, 4],通常以姿态模型代替实际的姿态[8, 9],而这种处理方法要求卫星姿态模型误差必须小于一定阈值,然而,针对姿态模型误差及其影响还鲜有文献进行过讨论,但是它对轨道的影响却不容忽视,因此,在讨论DORIS、GPS和SLR精密定轨策略前,首先要对Jason-2卫星姿态模型误差及其轨道影响进行评估。
卫星精密定轨策略研究的另外一个问题是数据融合问题,Jason-2卫星同时兼具GPS、SLR和DORIS 3种定轨手段,针对如何综合各定轨手段获得更加可靠、稳定和一致的轨道,文献[2, 5, 6, 7, 8]分别讨论了数据融合方法,然而这些数据融合方法均建立在大量的数据处理经验之上,具有很强的主观性,因此,本文探讨以轨道精度评估结果进行轨道叠加的效果。
本文首先对Jason-2卫星姿态模型误差及其轨道影响进行评估,而后分别讨论了GPS、SLR和DORIS 3种定轨手段的定轨策略,并采用不同的轨道评估方法对3种定轨手段的定轨精度进行了评估,最后基于轨道评估结果对轨道进行综合叠加,探讨基于轨道评估结果进行轨道叠加的效果。本文的研究内容,可以为我国海洋二号卫星精密定轨分析工作提供经验。
2 卫星姿态模型误差分析姿态模型误差的轨道影响是定轨策略中首要解决的问题,因为在卫星精密定轨中,难以精确获取实际姿态,通常以姿态模型代替实际的姿态[8, 9],但这种处理方法要求卫星姿态模型误差必须小于一定阈值。因此,在讨论DORIS、GPS和SLR精密定轨策略前,首先要讨论Jason-2卫星姿态模型误差及其对定轨精度影响。
2.1 姿态模型误差评估模型
假设卫星在J2000.0下位置和速度为:(X0,Y0,Z0,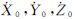 ),仪器的相位中心在卫星固定坐标系(SBF)和地心惯性系(J2000.0)下坐标分别为(XVc,YVc,ZVc)和(X0c,Y0c,Z0c)。
),仪器的相位中心在卫星固定坐标系(SBF)和地心惯性系(J2000.0)下坐标分别为(XVc,YVc,ZVc)和(X0c,Y0c,Z0c)。
关于SBF和J2000.0坐标系统的详细定义参考文献[11, 12, 13]。两者之间的转化关系为[12]
式中,R0、R1和R2分别为转换矩阵,其定义为
式中,A1、A2、A3、ROTy、ROTx、Rxy和α采用式(4)计算
而Ψ主要由轨道角Ω和beta角β′决定,而Ψ与Ω和β′的相互关系确定了卫星的姿态模型,根据Ω和β′的角度关系,Jason-2卫星姿态模型分成了固定姿态模式、正弦姿态模式、名义姿态模式和姿态翻转模式4种姿态调整模式[13]。
姿态模型决定了转换矩阵R2(Ψ)[10],若定义Ratt=R0·R1·R2,则Ratt描述的为基于姿态模型获得的卫星固定坐标系到J2000.0下的转换矩阵,假定实际姿态转移矩阵为R′att,则通过比较R′att与Ratt的差异,可以评估姿态模型误差大小。设
基于R′att和Ratt计算3个坐标轴指向角度偏差δαj,即
通过统计δαj的离散度,可反映出姿态模型误差的大小。由于卫星实际姿态是无法获得的,考虑到实测姿态具有较高的精度,因此,本文以实测姿态代替实际姿态分析姿态模型误差对不同观测手段的影响。
2.2 姿态模型误差分析基于δαj可以对卫星姿态模型误差进行评估,同时通过实测姿态矩阵R′att和模型姿态矩阵Ratt分别进行定轨计算并统计两者轨道的差异,可以评价姿态模型误差对轨道的影响,姿态的评估结果采用式(3)
式中,M为评估采用的天数;n为每天的历元数;j为坐标轴轴向。
轨道精度评估采用如下方法
式中,Xij和X′ij分别为基于姿态模型矩阵Ratt和实测姿态矩阵R′att计算的卫星在i历元、j轴方向上坐标。Δpl为轨道位置差异RMS,Δ为Δpl的均值,k和n分别为参与轨道统计的天数和历元数。通过计算,姿态模型误差在3个方向上分别为0.93°、1.030°和0.718°,对DORIS、GPS和SLR轨道的位置影响分别为0.042 m、0.036 m和0.033 m,径向影响分别为0.010 m、0.011 m和0.009 m。
3 卫星精密定轨分析 3.1 卫星定轨策略卫星精密定轨策略是卫星精密定轨中首要解决的问题。Jason-2卫星同时搭载了GPS、SLR和DORIS 3种定轨手段,这些测量设备相对于先前一代设备从测量精度和可靠性方面均有所提高[1, 5, 6],因此,Jason-2卫星定轨策略解决的是如何基于不同手段的高精度观测量来确定高精度和稳定性的卫星轨道。
卫星精密定轨策略主要涉及以下几个方面:①弧段长度(解算每组轨道所需要的数据长度);②参数化(参数估计类型、数目及先验权);③数据编辑(包括数据的剔除、权确定)[4, 5, 11, 12, 13]。
在以往的精密定轨处理策略中,GPS简化动力学定轨通常采用30 h数据,而DORIS和SLR定轨采用3 d短弧或1周的数据[1, 5]。参数化是卫星定轨策略研究中极为重要的问题,尤其是经验加速度的设置和约束问题,直接影响到定轨的精度[5, 13, 14, 15]。在卫星精密定轨策略研究中,另外一个重要的问题是数据剔除。通常数据剔除是在迭代中通过残差逐步实施,对于整体残差离群的异常观测站,需要对该站进行剔除[16, 17, 18, 19];先验权的设定主要根据不同的处理形式而采用不同的定权方案[19, 20, 21, 22]。由于Jason-2卫星定轨策略涉及内容较多,不再赘述,具体定轨策略详见表 1。
| 地球物理模型 | GPS | 地球重力场/潮汐和章动模型 | EIGEN2/(IERS2000/IAU2000) |
| 行星星历 | DE200 | ||
| 地球定向参数 | IERS C04 | ||
| DORIS/SLR | 地球重力场/潮汐模型 | JGM3/GOT99.2 | |
| 行星星历/大气密度 | DE403/MSIS-86 | ||
| 地球定向参数 | IERS C04 | ||
| 观测数据 | GPS | 2009-01-21-2009-01-25,非差观测量,等权处理 | |
| SLR | 2009-01-20-2009-01-27,SLR距离观测,等权处理 | ||
| DORIS | 2009-01-20-2009-01-27,多普勒观测量,等权处理 | ||
| 测量模型 | 相位中心 | GPS:星固系(SBF X,Y,Z):(1.194,-0.598,0.703)m | |
| SLR:星固系(SBF X,Y,Z):(1.194,-0.598,0.684)m | |||
| DORIS:星固系(SBF X,Y,Z):(2.385,-0.217,0.521)m | |||
| GPS卫星 | IGS 15 min精密星历、30 s精密钟差 | ||
| 姿态 | GPS/SLR/DORIS均采用卫星姿态模型 | ||
| SLR/DORIS站坐标 | ILRS(International SLR Service)/IDS(International DORIS Service)提供 | ||
| 估计参数 | 测量模型 | GPS:GPS载波相位模糊度;星载GPS接收机钟差 | |
| DORIS:DORIS测量偏差;对流层尺度因子(每个弧段) | |||
| 力学模型 | GPS:轨道6参数;CODE光压9参数;随机脉冲24组/d | ||
| DORIS:卫星位置和速度;每8 h一组大气阻力CD和变化率ĊD;每天一组经验加速度(切向和法向) | |||
| SLR:卫星位置和速度;每天一组大气阻力CD和变化率ĊD;每天一组经验加速度(切向和法向) | |||
| 弧段长度 | GPS:30 h弧段:前24 h为最终定轨结果,后6 h参与轨道弧段重叠检验 | ||
| SLR/DORIS:3 d弧段,中间一天为最终定轨结果,末尾一天前6 h弧段重叠 | |||
| 定轨软件 | GPS:BERNESE GPS Software V5.1 DORIS/SLR:UTOPIA | ||
SLR具有观测精度高(可达1 cm)、无模糊度和不受电离层影响等特点。因此,通常采用受较小大气影响的高角度激光观测量对轨道进行评价,然而高角度的观测量通常相对较少,对于3 d弧段的短弧段轨道评价,就缺乏足够的稳定性和可靠性[2, 10]。因此,为了获取稳定可靠的评估结果,文中采用15°的低角度激光观测数据。评估采用如下方法
式中,ρoi为激光观测值;ρci为基于待评估轨道计算的站心距;Δρalli为各类影响的等效距离和(包括测站偏心、测站偏移、大气延迟、海潮负荷、固体潮、质心改正和广义相对论效应改正)[3];εi为观测误差;δR为每日的SLR残差RMS值。
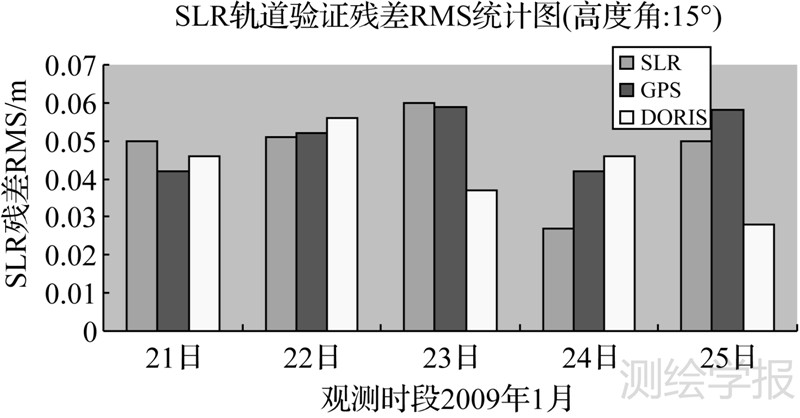
基于上述方法,笔者分别对GPS、SLR和DORIS定轨结果进行了评价,并统计了各天RMS的均值和方差,结果见图 1。SLR验证GPS、DORIS、SLR轨道各天残差RMS统计图和表 2各天残差RMS均值和方差统计表。其中表 2各天残差RMS均值和方差统计表为各天残差RMS均值和方差统计值,表中反映出DORIS定轨结果略优于SLR和GPS定轨结果,然而,由于SLR轨道本身是由SLR观测量计算而来,因此,通过SLR无法获得真实的SLR轨道精度。但是,SLR验证可以反映出DORIS定轨结果略优于GPS定轨结果。
|
| 图 1 SLR验证GPS、DORIS、SLR轨道各天残差RMS统计图 Fig. 1 Statistical value of every day for GPS,DORIS and SLR validated by SLR |
| m | |||
| SLR | GPS | DORIS | |
| 均值 | 0.048 | 0.051 | 0.043 |
| 均方差 | 0.012 | 0.008 | 0.011 |
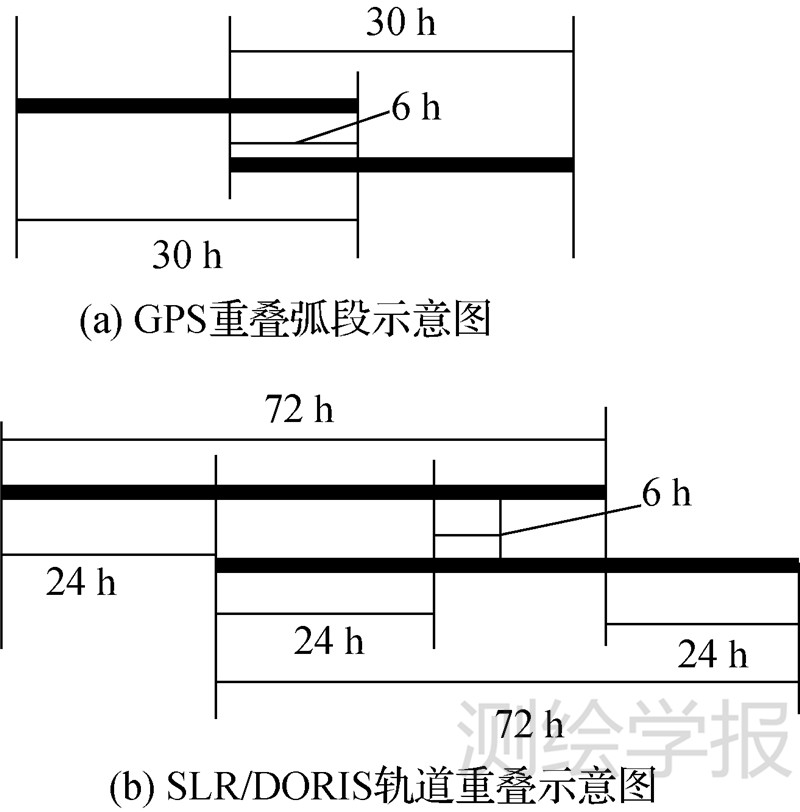
重叠弧段比较是基于独立解算轨道的部分重叠弧段进行比较,然后基于统计结果作为轨道精度评估的依据。GPS、SLR和DORIS的轨道重叠方式如图 2所示。
|
| 图 2 LR、DORIS和GPS轨道重叠方式示意图 Fig. 2 Schematic diagram of orbit overlap for SLR,DORIS and GPS |
针对3种手段的每个定轨弧段,均进行6 h的轨道重叠比较,然后,计算弧段重叠部分的位置差异RMS,其计算方法如下所示[10, 15]
式中,X1、Y1、Z1和X2、Y2、Z2分别为轨道重叠部分的坐标位置;而δX、δY、δZ分别为重叠段的3个方向差异的RMS值。
限于篇幅,本文仅给出重叠弧段的位置差异RMS值(见表 3)。通过重叠弧段比较反映出DORIS定轨结果要优于GPS和SLR,且呈现较好的稳定性,其位置差异RMS为3 cm左右;SLR定轨精度优于GPS结果,两者轨道精度差异为2.9 cm。然而轨道重叠反映的是轨道的自洽程度,与估计的轨道参数数目密切相关,由于GPS定轨所估计的轨道参数个数明显大于SLR和DOIRS,引起轨道的平滑性和自洽性偏差。
| m | |||
| 时段 | SLR | GPS | DORIS |
| 2009-01-21 | 0.070 | 0.053 | 0.036 |
| 2009-01-22 | 0.029 | 0.089 | 0.034 |
| 2009-01-23 | 0.026 | 0.086 | 0.022 |
| 2009-01-24 | 0.031 | 0.056 | 0.019 |
| 2009-01-25 | 0.059 | - | 0.053 |
| 均值 | 0.043 | 0.071 | 0.033 |
| 均方差 | 0.020 | 0.019 | 0.013 |
外部轨道比较是轨道评估中一种重要的轨道精度评价方式。该方式通过将计算的最终轨道与其他分析中心解算的轨道进行比较,反映出基于不同软件、不同测量模型和力学模型所引起的轨道差异。
文中采用JPL公布的Jason-2试验阶段的轨道,该轨道是基于GPS数据,采用简化动力学定轨方法计算得到的,其径向精度优于2 cm[1, 2, 3]。
通过将DORIS、GPS和SLR定轨结果分别与JPL简化动力学轨道进行比较,基于每天轨道差异的RMS,可反映出轨道的相对精度。文中仅给出位置差异RMS,结果显示:基于外部轨道比较方式,DORIS结果无论在精度和稳定性方面略优于SLR和GPS,其中SLR轨道结果略差,其位置差异在14 cm左右。
| m | |||
| 时段 | SLR | GPS | DORIS |
| 2009-01-21 | 0.136 | 0.098 | 0.084 |
| 2009-01-22 | 0.111 | 0.118 | 0.074 |
| 2009-01-23 | 0.139 | 0.124 | 0.082 |
| 2009-01-24 | 0.174 | 0.117 | 0.065 |
| 2009-01-25 | 0.137 | 0.120 | 0.068 |
| 均值 | 0.139 | 0.115 | 0.075 |
| 均方差 | 0.022 | 0.010 | 0.008 |
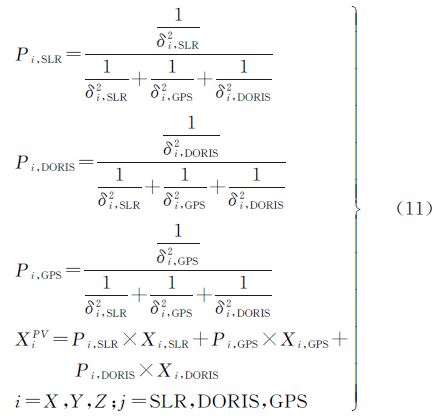
Jason-2卫星同时搭载有GPS、SLR和DORIS定轨手段,轨道叠加的目的是充分利用3种手段,获得更加稳定可靠的轨道结果[1, 5]。本文分别依据上述3种轨道评价方法的结果来进行轨道叠加。叠加时,首先根据轨道的评价结果,赋予不同手段的轨道以权系数,然后叠加生成一组轨道解,具体叠加方法如下所示
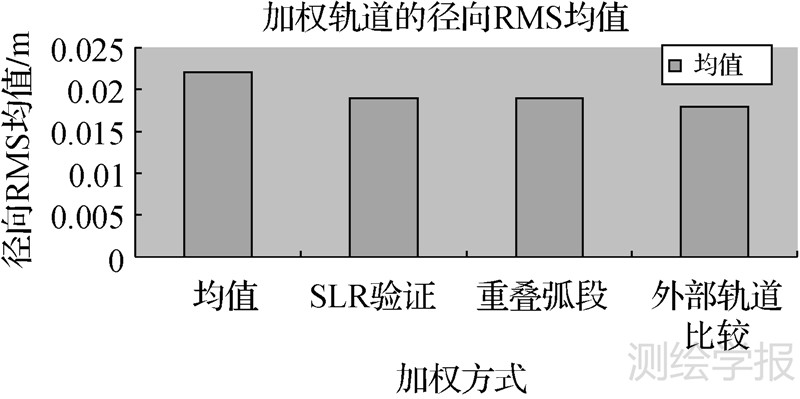
式中,Xi,SLR、Xi,GPS、Xi,DORIS分别为方向,SLR/GPS/DORIS的坐标值;Pi,SLR、Pi,GPS、Pi,DORIS分别为i方向,SLR/GPS/DORIS的权系数;δi,GPS、δi,SLR、δi,DORIS分别为i方向,GPS/SLR/DORIS的均方误差;XiPV为i方向叠加的轨道结果。由于缺少2009-01-25 GPS重叠弧段轨道精度,因此该段数据叠加时将其权系数设置为0。叠加后,通过将叠加的轨道与JPL标准轨道比较,得出其径向分量差异[2, 3]。此外,文中还采用了均值加权来进行轨道叠加,该方法假定3种手段的权完全一致。图 3为不同加权方法轨道经向差异的RMS均值。
|
| 图 3 不同加权方法轨道径向差异RMS均值 Fig. 3 RMS of orbit radial difference by using different weighting method |
表 5为基于4种加权方法得到的轨道与JPL轨道径向分量和位置差异的RMS值。通过表 5可以看出:均值加权方式要略差一些,因为它是一种完全无先验信息的加权;外部轨道比较加权方式最优,但是实际中这种加权方式是不可能实现的(基于某一轨道比较结果加权,而后再与此轨道比较);SLR验证和重叠弧段加权方式具有相似的精度,但是SLR定轨结果与SLR定权存在相关性,因此在实际卫星应用中,采用重叠弧段加权形式,可以获得比较高的轨道精度和可靠性。表 5反映出基于姿态模型定轨结果,以轨道重叠评估结果进行轨道叠加,其轨道径向精度优于2 cm。
| m | |||||||||||
| 时段/3种叠加方法 | 均值 | 重叠弧段 | SLR验证 | 外部轨道比较 | |||||||
| 径向 | 位置 | 径向 | 位置 | 径向 | 位置 | 径向 | 位置 | ||||
| 2009-01-21 | 0.020 | 0.060 | 0.019 | 0.051 | 0.017 | 0.053 | 0.017 | 0.054 | |||
| 2009-01-22 | 0.024 | 0.061 | 0.021 | 0.057 | 0.021 | 0.055 | 0.019 | 0.053 | |||
| 2009-01-23 | 0.017 | 0.060 | 0.012 | 0.055 | 0.015 | 0.053 | 0.014 | 0.050 | |||
| 2009-01-24 | 0.019 | 0.077 | 0.014 | 0.065 | 0.017 | 0.060 | 0.015 | 0.059 | |||
| 2009-01-25 | 0.029 | 0.069 | 0.027 | 0.059 | 0.027 | 0.057 | 0.027 | 0.057 | |||
| 均值 | 0.022 | 0.065 | 0.019 | 0.055 | 0.019 | 0.056 | 0.018 | 0.055 | |||
| 均方差 | 0.005 | 0.008 | 0.006 | 0.005 | 0.005 | 0.003 | 0.005 | 0.004 | |||
本文对SLR、DORIS和GPS 3种定轨手段的定轨策略与定轨精度问题进行了讨论,首先分析Jason-2卫星姿态模型误差及其对卫星精密定轨精度的影响,而后基于实测数据分别采用3种手段对2009-01-21-2009-01-25的Jason-2卫星的轨道进行了计算,并通过JPL精密轨道比对、轨道重叠检验以及SLR检验3种不同的轨道评估方法对3种定轨手段定轨的精度进行了评估,最后基于轨道评估结果进行了轨道叠加,对3种手段联合定轨的精度进行了分析,通过试验得出以下结论。
(1) 基于实测数据对Jason-2卫星进行姿态模型误差评估,表明其姿态模型误差在各方向上分别为0.93°、1.030°和0.718°,对DORIS、GPS和SLR轨道的位置影响分别为0.040 m、0.036 m和0.033 m,径向影响分别为0.010 m、0.011 m和0.009 m。
(2) 通过SLR检验、轨道重叠检验以及JPL精密轨道比对3种轨道评估方法表明:当无姿态数据时,基于姿态模型进行精密定轨,DORIS定轨结果略优于SLR和GPS定轨结果;轨道重叠检验和SLR验证体现出SLR定轨结果略优于GPS结果,而JPL轨道比较却表明GPS结果略优于SLR结果。考虑到SLR验证和轨道重叠评估方法本身存在的缺点,因此,在无姿态数据定轨时,DORIS定轨精度与GPS精度相当,略优于GPS定轨方法,SLR定轨精度较差。
(3) 轨道评估结果可为轨道叠加提供必要的信息,基于轨道重叠结果对GPS、SLR和DORIS在无姿态数据的定轨结果进行加权生成精密轨道时,可以得到比较高精度和可靠性的结果,叠加后,其轨道径向精度优于2 cm。
致谢:美国俄亥俄州立大学的C.K Shum提供Jason-2星载GPS资料,CSR研究中心John C. Ries、台湾交通大学Cheinway Hwang及AVISO的Soudarin Laurent在卫星定轨策略方面给予很多指导,在此表示感谢。
| [1] | STAVROS A M, FRANK G L, NIKITA P Z, et al. Status of Precise Orbit Determination for Jason-2 Using GPS, SLR, DORIS Data at NASA/GSFC[C]//Proceedings of EGU General Assembly 2011. Aarhus:[s.n.],2011. |
| [2] | LEMOINE F G, ZELENSKY N P, CHINN D S, et al. Towards Development of a Consistent Orbit Series for TOPEX/Poseidon, Jason-1 and Jason-2[J]. Advances in Space Research, 2010,46(12): 1513-1540. |
| [3] | BERTIGER W I, BAR-SEVER Y E, CHRISTENSEN E J, et al. GPS Precise Tracking of Topex/Poseidon: Results and Implication[J]. JGR Oceans Topex/Poseidon Special Issue, 1994, 99(C12):24449-24464. |
| [4] | CERRI L. Preliminary Strategy for Jason-2 POD[C]//DORIS Analysis Working Group Meeting (AWG) of the International DORIS Service. Paris:[s.n.], 2008. |
| [5] | HAINES B,BERTIGER W,DESAI S,et al.Initial Orbit Determination Results for Jason-1:Towards a 1-cm Orbit[C]//Proceedings of ION GPS 2002. Portland:[s.n.],2002. |
| [6] | ZHANG Feipeng, HUANG Cheng, LIAO Xinhao. Precise Orbit Determination of ERS-2 Satellite Using Several Observation Technologies[J]. Chinese Science Bulletin,2001,46(14): 1227-123. |
| [7] | NIKITA P Z, FRANK G L, MAREK Z, et al.DORIS/ SLR POD Modeling Improvements for Jason-1 and Jason-2[J]. Advances in Space Research, 2010. |
| [8] | DACH R, SCHAER S, BOCK H, et al. CODE’s New Combined GPS/GLONASS Clock Product[C]//Proceedings of the International GNSS Service. Newcastle:[s.n.], 2010. |
| [9] | HUGENTOBLER U, DACH R, FRIDEZ P. Bernese GPS Software Version 5.0[M]. Bern: [s.n.],2005. |
| [10] | HWANG C W, TSENG T P, LIN T J, et al.Quality Assessment of FORMOSAT-3/COSMIC and GRACE GPS Observables: Analysis of Multipath, Ionospheric Delay and Phase Residual in Orbit Determination [J]. GPS Solutions, 20(14):121-131. |
| [11] | ZHAO Qile. Research on Software and Theory of Precise Orbit Determination of GPS Navigation Constellation Satellite and LEO satellite[D].Wuhan: Wuhan University,2004.(赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉:武汉大学,2004.) |
| [12] | TAPLEY B D,SCHUTZ B E, BORN G H. Statistical Orbit Determination[M]. Copenhagen: Elsevier, 2004. |
| [13] | BEUTLER G, JGGI A, HUGENTOBLER U, et al. Efficient Satellite Orbit Modeling Using Pseudo-stochastic Parameters[J]. Journal of Geodesy, 2006, 80(7):353-372. |
| [14] | JAGGI A, HUGENTOBLER U, BOCK H, et al. Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data[J]. Advances in Space Research, 39(10):1612-1619. |
| [15] | JAGGI A, BOCK H, FLOBERGHAGEN R. GOCE Orbit Predictions for SLR Tracking[J]. GPS Solutions, 15(2): 129-137. |
| [16] | BOCK H, DACH R, JAGGI A, et al. High-rate GPS Clock Corrections from CODE: Support of 1Hz Applications[J]. Journal of Geodesy, 2009, 83(11): 1083-1094. |
| [17] | SHENG Chuanzhen,YUAN Yunbin, SUN Baoqi. Precise Orbit Determination of GPS Navigation Constellation Based on Global IGS Data[J]. Journal of Geodesy and Gedynamics,2011(1):138-141. (盛传贞,袁运斌,孙保琪.基于全球IGS数据的GPS导航星座精密轨道确定[J].大地测量与地球动力学,2011(1):138-141.) |
| [18] | HAN Baomin. Research on Theory of Kinematic Orbit Determination of LEO Satellite[D]. Wuhan: Chinese Academy of Sciences,2003.(韩保民. 星载GPS低轨卫星几何法定轨理论研究[D]. 武汉: 中国科学院测量与地球物理研究所,2003.) |
| [19] | OU Jikun. A Uniform Expression of Solutions of Ill-posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica,2004(4):283-288.(欧吉坤. 测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报,2004,(4):283-288.) |
| [20] | GAN W J, ZHANG P Z, SHEN Z K, et al. Present-day Crustal Motion within the Tibetan Plateau Inferred from GPS Measurements[J]. Journal of Geophysical Research, 2007, 112: B08416-B08429. |
| [21] | ZHAO Chunmei, QU Feng, CHENG Pengfei, et al. Data Quality Analysis of Argentina San Juan Laser Ranging[J]. Acta Geodaetica et Cartographica Sinica, 2008, 27(3):338-341.(赵春梅,瞿锋,程鹏飞,等.阿根廷圣胡安激光测距系统的SLR数据质量分析[J].测绘学报,2008, 27(3):338-341.) |
| [22] | SUN Baoqi, OU Jikun, SHENG Chuanzhen, et al. Optimal Multi-frequency Data Combination for Compass Cycle Slip Detection and Reparation[J]. Geomatics and Information Science of Wuhan University, 2010,10(2): 1157-1160.(孙保琪, 欧吉坤,盛传贞,等.一种适于Compass周跳探测的三频数据优化组合[J].武汉大学学报:信息科学版,2010,10(2): 1157-1160.) |