2. 地理信息工程国家重点实验室，陕西 西安 710054；
3. 西安测绘研究所，陕西 西安 710054；
4. 武汉大学 地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079；
5. 总装备部 工程设计研究总院，北京 100028
2. Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China;
3. National Key Laboratory of Geo-Information Engineering,Xi’an 710054,China;
4. Key laboratory of Geo-space Environment and Geodesy of Ministry of Education,Wuhan University,Wuhan 430079,China;
5. Center for Engineering Design and Research under the Headquarters of General Equipment,Beijing 100028,China
1 引 言
随着科技的进步与发展，重力数据的获取不再局限于传统的地面重力测量，利用快速高效的航空重力或卫星重力测量方法测量载体飞行高度面的重力异常，然后通过数学手段求得地面重力异常，成为获取大面积区域尤其是地面重力观测难以进行区域重力数据的重要方法，由此产生了将空中重力异常向下延拓至地面高度的需求。
众所周知，向下延拓属于地球物理反问题，一般难以获得稳定解。对此，国内外学者展开了深入研究，获得了众多具有理论意义或实际应用价值的成果。目前，航空重力数据向下延拓主要有以下几种方法：正则化法、配置法、迭代法、“倒锥法”、直接代表法、点质量法，等。严格来说，迭代法属于正则化法的一种，但本文将其单独作为一种方法，因为迭代法与正则化法在正则化参数的选择方面有较大不同。
文献[1, 2]探讨了正则化方法在向下延拓中的应用，比较分析了正则化参数选取的方法以及效果。文献[3]将最小二乘配置法应用于重力数据的向下延拓。文献[4]提出了向下延拓重力数据的“倒锥法”，能够完成高精度的向下延拓计算。文献[5, 6]分析了地面与航空重力数据的频域特征，指出随着高度的增加，空中重力异常的频谱衰减剧烈，并据此提出了直接代表法，以空中重力异常作为地面重力异常的低频项，利用DEM数据进行向下延拓的高频改正，得到了较为满意的结果。文献[7]比较分析了多种向下延拓方法的精度，说明了正则化方法的优势所在。文献[8]详细研究了“移去—恢复”方法在向下延拓正则化方法中的应用，指出该方法能够提高正则化方法向下延拓的精度。文献[9]提出基于多尺度边缘约束的重力场信号向下延拓方法，进一步丰富了向下延拓的理论与方法。文献[10]比较了Tikhonov正则化、岭估计和广义岭估计应用于向下延拓的效果，指出广义岭估计相比其余两种延拓方法在精度、稳定性和抗差性方面均具有更好效果。文献[11]提出基于信噪比的正则化方法并将其用于航空重力向下延拓。文献[12]详细分析了地形对向下延拓的影响，文献[13]从Poisson积分公式出发，研究了向下延拓的不同机制，指出点延拓与面延拓应采用不同的平滑因子，从而减小离散误差的影响。文献[14]比较了3种迭代正则化方法，并以球体重力场模型为基础对实际延拓效果进行了分析。
这些方法的提出与应用，一定程度上解决了重力场向下延拓的精度问题，但仍然存在一些不足。以正则化方法为例，该方法需要准确选取正则化参数并需要进行大型矩阵的奇异值分解计算，计算速度非常慢，无法应用于大面积区域；配置法由于协方差函数确定的巨大困难导致该方法延拓精度有限；“倒锥法”需要在延拓区域有地面实测重力数据的支持，通常难以满足。
本文引入迭代Tikhonov正则化方法，利用其空间域和波数域两类迭代求解航空重力异常的向下延拓，并与Tikhonov正则化方法作比较，得出一些有益的结论，为后续研究提供一定的参考。
2 向下延拓的数学模型重力异常的向上延拓是关于球外部Dirichlet问题的求解过程，其结果由球近似下的Poisson积分公式给出[15]
式中，R为地球平均半径；Δgh、Δg分别为空中与地面重力异常；r=R+h；h为向上延拓高度；(φ,λ)和(φ′,λ′)分别为空中计算点与地面流动点的坐标；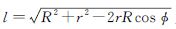
为两点间距离，为两点间球面角距，可由式(2)计算
在不影响精度的条件下，式(1)可平面近似为
对于式(1)，已知Δgh求解Δg的问题即为重力异常的向下延拓。通常，反问题都是不适定问题。此时式(1)为第一类Fredholm积分方程，当Δgh存在误差时，直接求逆结果极不稳定，从而限制了向下延拓重力异常的精度。
3 向下延拓的正则化方法 3.1 Tikhonov正则化方法及其谱分解在求解地球物理反问题的方法中，正则化方法作为一种重要理论在其中起着不可替代的作用，而其中尤以Tikhonov提出的正则化方法[16]应用最为广泛，其基本思想为[1]：求解参数x的估值，使得
式中，α＞0为正则化参数。由式(4)的约束条件，可以得到x的正则化解表达式为 对系数阵A进行奇异值分解得 式中，U、V分别是A的左右酉矩阵，U=[ui]，V=[vi]，i=1,2,...,n；Λ为对角阵，其对角线元素由A矩阵的奇异值λi按照递减的次序排列而成。则式(5)的谱分解形式为
由式(7)可以看出，正则化参数α调整奇异值单调趋于0的趋势，改善了最终解的稳定性。利用Tikhonov正则化方法求解不适定问题的关键在于正则化参数α的选取，主要方法有广义交叉验证(GCV)法[17]、L-曲线法[18]、图解-数值迭代法[1]等。
GCV法基本原理是：选取参数α，使得GCV函数
取得最小值，其中tr()表示矩阵的迹，Qα=A(αI+ATA)-1AT。显然，GCV法求取正则化参数的过程是迭代计算的过程。
L-曲线法的原理是：选取适当的参数α，以平衡
的值。实际操作时，选取L-曲线
的拐点所对应的参数，此α值即为所求最佳正则化参数。
空间域Tikhonov迭代法(以下简称空间域迭代法)可表示为[19, 20]
式中，n为迭代次数，xαn、xαn－1分别为第n次、第n－1次迭代后x的值，其余各参数定义与上文相同。式(9)可进一步写为 式(10)即为空间域迭代法的实用公式。给定最大迭代次数N或很小的正数ε，当满足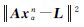
＜ε或n=N时停止迭代。可以证明[19]，对于给定的正数α，当n→∞时，xαn→x。
3.3 波数域Tikhonov迭代法由于向上延拓过程稳定可靠，故可直接采用快速傅里叶算法(FFT)计算。式(3)右端是卷积形式，据此，文献[21]导出了向上延拓算子为Φ(ω)=e－ωh，称为原始延拓算子，则式(3)的波数域表达式为[22]
式中，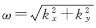
为角频率，kx、ky分别表示在x和y方向的波数；X、Y分别表示x、y在波数域的象；h为延拓高度。设x和y方向共包含M×N个点，则认为其波长分别为λx=Mdx，λy=Mdy，dx、dy表示x和y方向的分辨率。设0≤m≤M，0≤n≤N，则对于(m,n)处的点其角频率可表示为
式(11)即为向下延拓的FFT法。
波数域Tikhonov迭代法(以下简称波数域迭代法)即在空间域迭代过程中引入FFT方法，将其转化到波数域进行迭代求解，然后通过傅里叶逆变换求得最终的延拓效果。对式(9)两边作傅里叶变换可得
根据文献[14]，由数学归纳法可以最终推得波数域迭代法的向下延拓算子为φ(ω)=eωh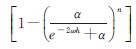
，n为迭代次数，α为给定正数。则波数域迭代法的最终表达式为
式中，F、F－1分别表示傅里叶变换和逆变换过程。
4 算例与分析
4.1 数据
本文将覆盖范围为1.5°×1.5°、分辨率为2′×2′的某区域实测地面格网平均重力异常用式(1)延拓至3500m高度，积分半径为30′，以此作为向下延拓的初始数据，以原始地面重力异常作为向下延拓结果的检核数据。地面(h=0m)重力异常以及h=3500m高度处航空重力异常数据统计情况列于表 1。
| mGal | ||||
| 最小值 | 最大值 | 平均值 | 标准差 | |
| h=0 | -65.44 | 45.94 | -29.53 | ±18.18 |
| h=3500 | -58.02 | 28.25 | -28.85 | ±14.67 |
为避免计算过程中边界效应对最终结果的影响，取30′为积分半径，计算全部区域向下延拓的结果，但在检核延拓效果时取位于该地区中央的1°×1°区域，因该区域数据受边界效应的影响较小；在延拓过程中，“移去—恢复”理论作为向下延拓的重要方法也同时加以应用，采用的参考模型为EGM2008全球重力场模型[23]的前360阶次。
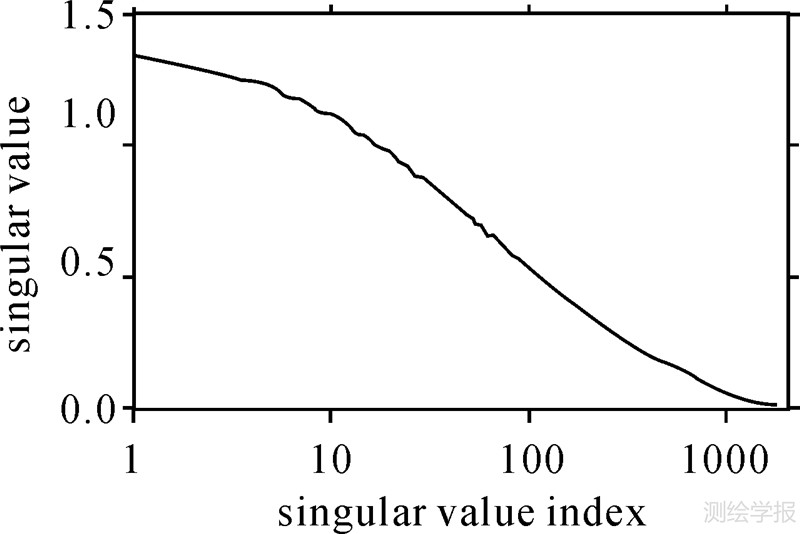
4.2 结果与分析 4.2.1 病态性分析及最小二乘解如上所述，向下延拓问题的法矩阵一般呈现出病态性特征，其条件数往往远超病态临界值1000。经计算，由该区域数据组成的法矩阵条件数高达13328，属高度病态矩阵，若直接采用最小二乘方法(LS)求解，将造成结果的极不稳定。系数阵的奇异值分布情况如图 1所示。
|
| 图 1 系数阵奇异值分布图 Fig. 1 Singular values of coefficient matrix |
由图 1可以看出，奇异值单调趋于0，这是造成最小二乘直接求逆计算结果不稳定的主要原因。直接求逆的结果与地面实际值的差值如图 2所示(经纬度坐标已经过处理，非实际坐标，下同)。
|
| 图 2 最小二乘法差值分布 Fig. 2 Error distribution of LS method |
从图 2可以看出，由于法矩阵严重病态，最小二乘直接求逆的向下延拓结果极不稳定，无法在实际数据处理过程中采用。
4.2.2 Tikhonov正则化法Tikhonov正则化方法能够调整奇异值趋于0的程度，从而改善最小二乘计算结果。基于GCV法和L-曲线法选取正则化参数，选取范围定为系数阵最大奇异值与最小奇异值之间[2]。GCV函数值随正则化参数α变化趋势以及L曲线如图 3(a)和图 3(b)所示。
|
| 图 3 GCV函数及L-曲线随α变化趋势示意图 Fig. 3 GCV function values and L-curve with different α |
由图 3可以看出，该区域GCV函数并不收敛，且L-曲线不存在拐点，只能选择曲率半径最小处作为L-曲线的解。这是Tikhonov正则化方法存在的主要问题。取最小GCV值对应的α参数值(L-曲线曲率半径最小处的α值与其相同)，则α=0.0117，对应系数阵最小奇异值。利用该α值进行Tikhonov正则化向下延拓，其最终结果与实际地面重力异常的差值分布如图 4所示。
|
| 图 4 Tikhonov正则化法差值分布 Fig. 4 Error distribution of Tikhonov regularization method |
比较图 2和图 4可以看出，Tikhonov正则化方法能够在一定程度上消除法矩阵病态的影响，但是在局部区域的延拓结果仍然存在较大误差，其原因可能是由于GCV函数不收敛，L-曲线拐点不存在，导致无法确定最优正则化参数，从而影响了最终的延拓效果。
4.2.3 空间域迭代法为了分析正则化参数对空间域迭代法延拓精度的影响，取不同的正则化参数，分别利用式(10)进行解算，其均方根值随迭代次数及正则化参数α的变化趋势如图 5所示。
|
| 图 5 空间域迭代Tikhonov正则化法精度变化趋势 Fig. 5 Space domain iterative Tikhonov regularization precision change with iterated times and α |
由图 5可以看出，空间域迭代法的延拓精度与迭代次数相关，迭代次数越多，精度越高；另外，随着α的减小，前几次迭代精度的变化越为明显；无论α的取值如何，迭代10次基本都能达到该方法所能达到的最高精度。
但图 5也说明了该方法的重要问题所在：即无论α如何取值，其精度变化曲线不收敛，这说明虽然理论证明式(10)收敛，仍然需要考虑其适用性问题。图 6是α=1、迭代次数为20时延拓结果与实际值的误差分布图，与图 4比较可以看出，两种方法的结果较为接近，仅有细微的差别。这说明，若不考虑收敛性问题，空间域迭代法由于对正则化参数不敏感，从而在应用时无需精确选取正则化参数，这是空间域迭代法相比Tikhonov正则化法的优势所在，此时起正则化作用的是迭代次数。
|
| 图 6 空间域迭代法差值分布 Fig. 6 Error distribution of space domain iterative method |
首先分析延拓算子在不同的迭代次数和正则化参数下的频率响应。为便于说明，频率响应分析按照一维情况处理，二维情况与一维相似，注意此处h=3500m。图 7(a)、图 7(b)分别是迭代次数为5次和50次时，不同的正则化参数所对应延拓算子的频率响应大小；图 8(a)、图 8(b)分别是正则化参数取0.05和0.5时，不同的迭代次数所对应延拓算子的频率响应大小。
|
| 图 7 不同迭代次数的频率响应 Fig. 7 Frequency response with different iterated times |
|
| 图 8 不同正则化参数的频率响应 Fig. 8 Frequency response with different regularization parameters |
比较图 7、图 8可以发现，波数域迭代法的延拓算子是带通滤波器，其最大频率响应随着迭代次数的增加而增大，随着正则化参数的增大而减小。当迭代次数过多时，其延拓精度会随着迭代的进行而变得极不稳定。从上述分析也可以看出，波数域迭代法与空间域迭代法类似，迭代次数在计算过程中起着正则化作用。图 9是波数域迭代法的向下延拓精度随迭代次数及α的变化趋势图，从中可以看出，无论α如何取值，随着迭代的进行，其结果先收敛后发散，且随着α的增大，收敛所需的迭代次数也在增加，例如α分别取0.05、0.5和1时，收敛所需的迭代次数分别为3次、38次和69次。
|
| 图 9 波数域迭代法精度随迭代次数及α的变化趋势 Fig. 9 Wave number domain iterative method precision change with iterated times and α |
取α=1、迭代69次作为波数域迭代法的计算参数，其向下延拓结果与实际值的差值分布如图 10所示。
|
| 图 10 波数域迭代法差值分布 Fig. 10 Error distribution of wave number domain iterative method |
表 2列出了4种方法精度及运算速度的比较统计情况，所用计算机为：Windows XP SP3操作系统，Matlab R2011b试验平台，主频3.2GHz，1GB内存。其中，统计消耗时间时，没有考虑系数矩阵构建所消耗的时间；两种迭代法的迭代次数均为100次，α均取为1，最终结果所对应的迭代次数分别为20次与69次；Tikhonov正则化方法所消耗时间包括系数矩阵奇异值分解、GCV函数计算所消耗时间，α取值0.0117。
| 差值 最大值/ mGal | 差值 最小值/ mGal | 差值 平均值/ mGal | 差值 均方根/ mGal | 消耗 时间/s |
| 最小二乘法 | 493.00 | -430.05 | 11.79 | 170.60 | 1.8 |
| Tikhonov正则化法 | 9.32 | -18.87 | -0.26 | 4.41 | 19.2 |
| 空间域迭代法 | 8.40 | -18.02 | -0.27 | 4.27 | 8.4 |
| 波数域迭代法 | 2.59 | -3.95 | -0.04 | 0.75 | 2.3 |
比较图 2、图 4、图 6、图 10以及表 2可以明显看出，在向下延拓精度方面，除去最小二乘法，波数域迭代法的精度最高，空间域迭代法次之，Tikhonov正则化法最低，其原因主要是由于后两种方法存在不收敛的现象，即对于Tikhonov正则化法，GCV函数不收敛，对于空间域迭代法，迭代过程不收敛。故两种方法虽然能够完成向下延拓的解算，但其精度受到较大限制。波数域迭代法的精度随着迭代次数的增加明显存在先收敛后发散的过程，其最终结果相比另外两种方法更加可靠。在消耗时间方面，波数域迭代法也有较大优势，空间域迭代法次之，Tikhonov正则化法最慢。其原因是由于迭代法需要进行矩阵求逆运算，而Tikhonov正则化法需要计算矩阵的奇异值分解，两种运算都非常消耗时间。
值得说明的是，若考虑计算机内存的问题，Tikhonov正则化法由于需要计算矩阵的奇异值分解，对内存的需求量巨大，例如上述试验所用计算机在进行5000阶以上矩阵的奇异值分解运算时会出现内存不够的问题，而迭代法消耗内存量相比Tikhonov正则化法较少，这一点在进行较大区域延拓计算时应加以考虑。
4.2.6 基于差异熵确定迭代次数由图 9可知，迭代法的关键在于确定准确的迭代终止条件，一般取广义交叉验证方法，但上文的研究已经表明，该方法不收敛，故此处无法应用。当地面重力异常未知时，每次迭代的结果精度无法评估，更加难以选择合适的迭代次数。为了准确确定不同的正则化参数对应的迭代次数，受信息熵概念的启发，提出一种基于差异熵的迭代次数确定方法。
地球物理学中，区域重力异常熵定义为[24]
式中，H(Δg)表示重力异常熵；p(Δgi,j)表示Δgi,j的概率。p(Δgi,j)理论上应使用大量数据经统计得出，但在区域范围内应用时也可直接计算 差异熵更能反映区域内重力异常的变化[24]，其定义与式(15)形式相同，所不同的是p(Δgi,j)。以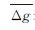
表示该区域重力异常的均值，定义Ci,j
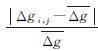，则
利用差异熵确定迭代次数的基本思想为：熵值体现了系统的不确定程度，较大的向下延拓误差体现为较大的熵值，故在每次迭代过程中，计算每次延拓结果的差异熵，最小的差异熵对应最高精度的延拓结果。该方法的主要误差源是p(Δgi,j)的计算，包含两个方面的因素：①无论采取何种手段，向下延拓的结果误差不可避免，导致p(Δgi,j)的计算误差；②利用部分数据样本代替总体概率统计所造成的误差，这应是主要的误差源所在。
为了验证所提方法的效果，在上述计算过程中加入差异熵的计算，根据最小差异熵获取不同的正则化参数所对应的迭代次数，并与图 9中实际最高精度对应的迭代次数作比较，其差值结果如图 11所示。
|
| 图 11 基于重力异常差异熵确定迭代次数的精度 Fig. 11 Precision of iterated times determination based on gravity anomaly variance entropy |
由图 11可以看出，基于差异熵的迭代次数确定方法是合理且有效的，当正则化参数小于1时，该方法确定的迭代次数与实际所需迭代次数差值在3次以内；若进一步缩小正则化参数的取值，则确定迭代次数的准确率更高，这充分验证了该方法的有效性。同时，该方法的准确性与正则化参数的大小存在一定关系，正则化参数选取较大时，其准确率有所降低，原因尚不清楚，故在实际应用时，建议选取较小的正则化参数(小于0.5)。
5 结 论本文针对重力异常向下延拓的病态性问题，引入迭代Tikhonov正则化方法，分别介绍了空间域和波数域两种迭代法的理论计算方法，并进行了3种方法的实际解算和比较，指出Tikhonov正则化方法和空间域迭代法存在的问题。通过以上计算和分析，可以得到如下几点结论：
(1) 在进行航空重力数据向下延拓的求解过程中，最小二乘方法所得结果极不稳定，采用不同的正则化方法能够不同程度地改善向下延拓的精度和稳定性。
(2) 对于Tikhonov正则化方法，使用GCV方法求解正则化参数时，GCV函数会不收敛；利用L-曲线法时会出现L曲线拐点无法确定的情况，此时得到的正则化参数虽然能够改善求解精度，但是限制了精度的进一步提高。
(3) 对于空间域迭代法，虽然理论证明该方法最终收敛，但是在实际应用时，对于固定的正则化参数，其均方根曲线存在不收敛的情况，其原因仍待进一步研究，在使用时应加以注意。
(4) 波数域迭代法将向下延拓问题转化为带通滤波器，从而实现快速、稳定的重力异常向下延拓，该方法计算速度快，稳定性好，精度高，通过迭代次数实现正则化，对正则化参数不敏感，故无需进行正则化参数的选取，且不会出现类似空间域迭代法或者Tikhonov正则化方法存在的不收敛问题，值得广泛用于航空重力异常向下延拓的解算。
(5) 针对迭代法迭代次数的确定问题，提出了基于重力异常差异熵的迭代次数确定方法，实际计算结果表明，该方法能够准确确定迭代次数，特别是当正则化参数取值较小时，效果更佳。
| [1] | WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 33-38.(王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及其谱分解[J]. 测绘学报, 2004, 33(1): 33-38.) |
| [2] | DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 690-696.(邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报, 2011, 40(6): 690-696.) |
| [3] | KELLER W, HIRSCH M. Downward Continuation versus Free Air Reduction in Airborne Gravimetry[C]//Geodesy and Physics of the Earth: Geodetic Contributions to Geodynamics. Berlin: Springer-Verlag, 1992: 266-272. |
| [4] | YANG Qiangwen, WU Xiaoping. “Qusai-cone Method”, a New Way of Downward Continuation of Airborne Gravimetry Data[J]. Journal of the PLA Institute of Surveying and Mapping, 1998, 15(3): 169-172.(杨强文, 吴晓平. 航空重力数据向下延拓的倒锥法[J]. 解放军测绘学院学报, 1998, 15(3): 169-172.) |
| [5] | SHI Pan, WANG Xingtao. Determination of the Terrain Surface Gravity Field Using Airborne Gravimetry and DEM[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2): 117-121.(石磐, 王兴涛. 利用航空重力测量和DEM确定地面重力场[J]. 测绘学报, 1997, 26(2): 117-121.) |
| [6] | SHI Pan, WANG Xingtao. The Frequency Domain Analysis of the Determination of Terrestrial Mean Gravity Anomaly Using Airborne Gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4): 301-308.(石磐, 王兴涛. 空中测量地面平均重力异常的频域分析[J]. 测绘学报, 1995, 24(4): 301-308.) |
| [7] | WANG Xingtao, XIA Zheren, SHI Pan, et al. A Comparison of Different Downward Continuation Methods for Airborne Gravity Data[J]. Chinese Journal of Geophysics, 2004, 47(6): 1017-1021.(王兴涛, 夏哲仁, 石磐, 等. 航空重力测量数据向下延拓方法比较[J]. 地球物理学报, 2004, 47(6): 1017-1021.) |
| [8] | HAO Yanling, CHENG Yi, SUN Feng, et a1. Simulation Research on Tikhonov Regularization Algorithm in Downward Continuation[J]. Chinese Journal of Scientific Instrument, 2008, 29(8): 2190-2194.(郝燕玲, 成怡, 孙枫, 等. Tikhonov正则化向下延拓算法仿真实验研究[J]. 仪器仪表学报, 2008, 29(8): 2190-2194.) |
| [9] | NING Jinsheng, WANG Haihong, LUO Zhicai. Downward Continuation of Gravity Signals Based on the Multiscale Edge Constraint[J]. Chinese Journal of Geophysics, 2005, 48(1): 63-68.(宁津生, 汪海洪, 罗志才. 基于多尺度边缘约束的重力场信号的向下延拓[J]. 地球物理学报, 2005, 48(1): 63-68.) |
| [10] | JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 684-689.(蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011, 40(6): 684-689.) |
| [11] | GU Yongwei, GUI Qingming. Study of Regularization Based on Signal-to-noise Index in Airborne Gravity Downward to the Earth Surface[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 458-464.(顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J]. 测绘学报, 2010, 39(5): 458-464.) |
| [12] | WANG Y M. The Effect of Topography on the Determination of the Geoid Using Analytical Downward Continuation[J]. Bulletin Godsique, 1990, 64: 231-246. |
| [13] | GOLI M, NAJAFI-ALAMDARI M, VANICEK P. Numerical Behaviour of the Downward Continuation of Gravity Anomalies[J]. Studia Geophysica et Geodaetica, 2011, 55: 191-202. |
| [14] | ZENG Xiaoniu, LI Xihai, HAN Shaoqing, et al. A Comparison of Three Iteration Methods for Downward Continuation of Potential Fields[J]. Progress in Geophysics, 2011, 26(3): 908-915.(曾小牛, 李夕海, 韩绍卿, 等. 位场向下延拓三种迭代方法之比较[J]. 地球物理学进展, 2011, 26(3): 908-915.) |
| [15] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. Beijing: Surveying and Mapping Press, 1979.(海斯卡涅W A, 莫里斯H. 物理大地测量学[M]. 北京: 测绘出版社, 1979.) |
| [16] | TIKHONOV A N. Solution of Ill-posed Problem[M]. New York: John Wiley & Arsenin, 1977. |
| [17] | KILMER M E, O’LEARY D P. Choosing Regularization Parameters in Iterative Methods for Ill-posed Problems[J]. SIAM Journal on Matrix Analysis and Applications, 2001, 22(4): 1204-1221. |
| [18] | HANSEN P C, O’LEARY D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. |
| [19] | ZHANG Luyin, ZHANG Yuhai, QIAN Kunming. On the Iterated Tikhonov Regularization for Ill-posed Problems[J]. Journal of Shandong University: Natural Science, 2011, 46(4): 29-33.(张路寅, 张玉海, 钱坤明. 关于不适定问题的迭代Tikhonov正则化方法[J]. 山东大学学报:理学版, 2011, 46(4): 29-33.) |
| [20] | KALTENBACHER B, NEUBAUER A, SCHERZER O. Iterative Regularization Methods for Nonlinear Ill-posed Problems[M]. New York: Walter de Gruyter, 2008. |
| [21] | DEAN W C. Frequency Analysis for Gravity and Magnetic Interpretation[J]. Geophysics, 1958, 23: 97-127. |
| [22] | HOU Zhongchu, LIU Xiufang. Gravity and Magnetic Field Conversion Using Two Dimension Fourier Transform[J]. Journal of Beijing Normal University, 1978, 14(2): 54-69.(侯重初, 刘秀芳. 用二维富氏变换进行重磁位场的转换[J]. 北京师范大学学报, 1978, 14(2): 54-69.) |
| [23] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289.(章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |
| [24] | XU Xiaosu, ZHANG Yiqun. Application of Modified Terrain Entropy Algorithm in Terrain Aided Navigation[J]. Journal of Chinese Inertial Technology, 2008, 16(5): 595-598.(徐晓苏, 张逸群. 改进的地形熵算法在地形辅助导航中的应用[J]. 中国惯性技术学报, 2008, 16(5): 595-598.) |