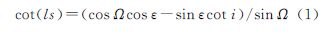2. 西安测绘研究所,陕西 西安 710054;
3. 极地测绘科学国家测绘地理信息局重点实验室,湖北 武汉 430079
2. Xian Research Institute of Surveying and Mapping,Xian 710054,China;
3. National Administration of Surveying,Mapping and Geoinformation Key Laboratory for Polar Surveying and Mapping Science,Wuhan 430079,China
1 引 言
在卫星导航及精密定轨中,地影指太阳、地球和卫星运行至几乎同一平面时,受地球遮挡,卫星星体不能接受到太阳光线照射并感知太阳位置的现象。
地影造成太阳无法照射到星上太阳能帆板,从而导致卫星能源不足,各部件温度发生变化,因此,需要对卫星温控策略进行调整,并对卫星敏感器件进行抗干扰保护[1]。故地影期成为卫星故障的高发期。对地影期的判断也同样制约着卫星姿态控制系统及精密定轨处理策略的切换[2, 3, 4, 5]。我国卫星导航系统采用GEO、IGSO高轨卫星,其轨道特性有别于GPS系统采用的MEO卫星。另外,我国在频繁过地影期采用类似日本QZSS导航系统的零偏置姿态控制策略,与GPS系统差异较大[6]。针对3类卫星分别进行卫星进出地影时间及在蚀状态判断可为卫星控制策略及精密定轨处理策略制定提供理论依据[7, 8, 9, 10]。
根据卫星距地球的高度,太阳光源形成的地影可近似为柱形和锥形两种形状。对中低轨道卫星,在半影区内的飞行时间也只有几秒,且一般不跨越伪影区,因此在精度要求不高时,可近似采用柱形地影模型[11]。但对于GEO、IGSO等高轨卫星而言,简化地影模型所带来的影响需进一步分析[12]。
太阳辐射压是卫星轨道确定中影响最大、最难精确模拟的非保守力,其与卫星受照面积、卫星与太阳的几何关系等相关。GEO、IGSO与MEO卫星在入地影频度、持续时间、最长日期变化等方面均有所不同,对地影期间动力学模型的影响程度也不同[13, 14]。因此地影状态分析也是卫星轨道确定的影响因素之一。
本文重点针对3类卫星进行锥形、柱形地影模型对比分析,并研究卫星地影状态与卫星轨道根数间的变化关系,为我国卫星导航系统高精度稳定运行提供理论支持。
2 地影模型地影的精确描述较为复杂,在航天工程中,一般假设地球呈球形,地球周围无大气,即不考虑地球大气对光线的折射效应[15, 16]。
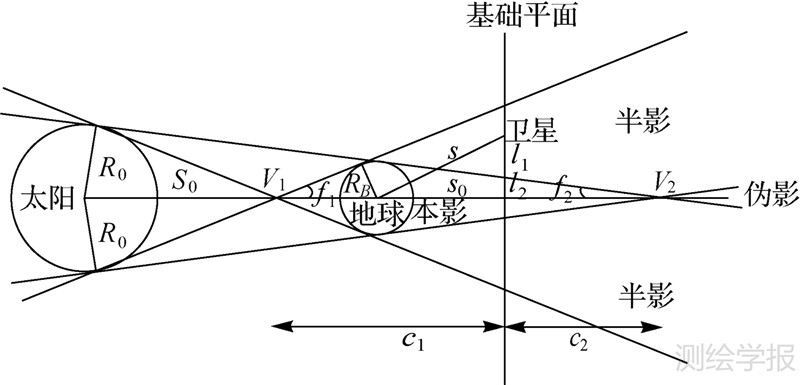
2.1 锥形地影模型若将太阳视为有大小的光源,则地影为两个同轴相套的圆锥,即锥形地影模型,如图 1[15, 16, 17]。
|
| 图 1 锥形地影模型 Fig. 1 Conical shadow model |
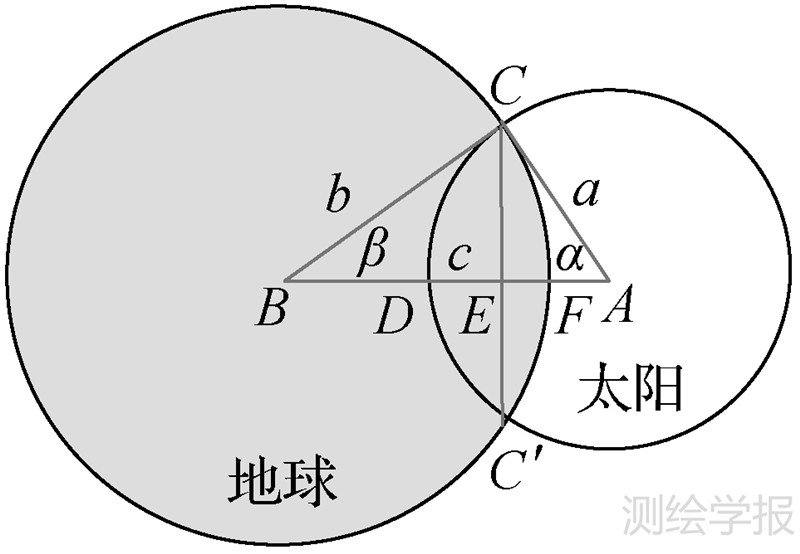
图 2地球对太阳的遮挡通常通过地影因子v反映[18]。若v=0表示太阳光照被完全遮挡,v=1表示完全处于太阳光照下;0<v<1表示光照被部分遮挡。地影因子的计算可利用太阳与地球视向相交圆推导获得。
|
| 图 2 太阳被地球遮挡示意图 Fig. 2 Occultation of the sun by the earth |
定义rB、re、r分别为遮挡体(地球)、太阳、卫星在惯性坐标系内的坐标。se=re-rB,s=r-rB分别为太阳和卫星相对遮挡体(地球)的坐标;R⊙、RB为太阳和地球的半径;a、b为太阳、地球视半径,c为太阳与地球中心的视距离。
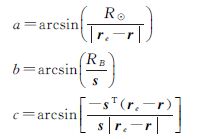
太阳的蚀面积A为
A=ACFC′+ACDC′
若|a-b|<c<a+b,则蚀面积A可表示为
A=2(ABCF-ABCE)+2(AACD-AACE)
定义AE=x,EC=y,∠CAE=α,则
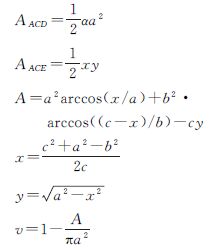
以上推导均是在|a-b|<c<a+b的假设下进行的。若该条件不成立,则当a+b≤c时,表示无遮挡;当c<b-a(即a<b)时,表示完全遮挡。
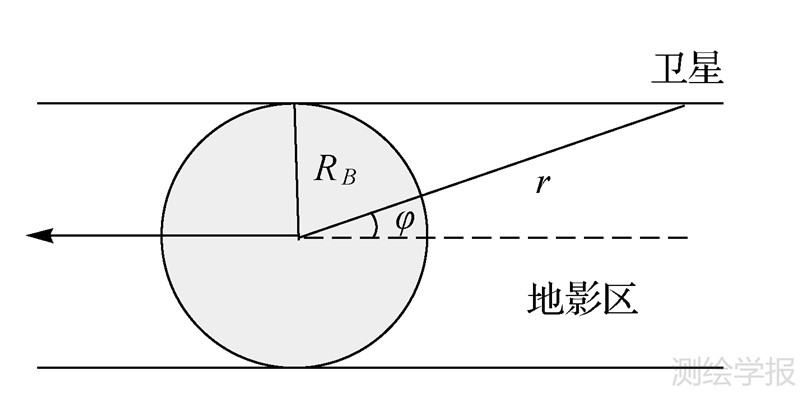
2.2 柱形地影模型由于太阳距地球较远,当卫星轨道比较低时,把太阳光束看做近似平行于日心与地心连线的平行光线,阳光被遮挡后产生一个柱形阴影(图 3)[11, 12, 13, 14, 15, 16, 17, 18, 19]。柱形地影因子的取值是当卫星在地影区时0,否则为1。根据图 3的几何关系,地影因子v的表达式为
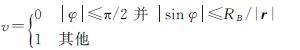
|
| 图 3 柱形地影模型 Fig. 3 Cylindrical shadow model |
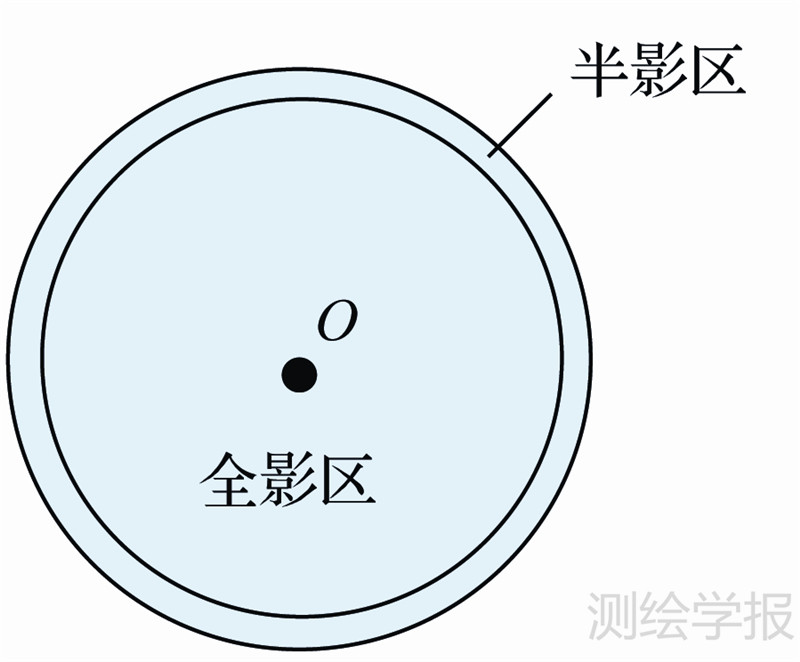
地球静止轨道是倾角为0°,半径为42164km的圆轨道。取地球半径为6371km,太阳半径为696000km,日地平均距离为1.496×108km,在GEO卫星处,地球和太阳的视直径分别为17.3814°、0.5333°。两视盘相对运动速度约为地球自转速度,即1°的运行时间约为4min。从相互外切开始,2min后地球视盘吞没太阳视盘,前半段的半影区结束,开始本影区,17°需要约68min完成穿越,然后是另外半段的半影区。由此可以得到地球阴影如图 4所示[3, 17]。图中O为地影中心,两圆半径分别为8.4240°和8.9574°。在两圆之间为半影区,在小圆之内为本影区。假设太阳赤纬为δs,当|δs|<8.4240°时,卫星每天穿过地影一次。地影时间可以用球面三角形方法解出。
|
| 图 4 地球阴影 Fig. 4 Earth′s shadow |
地影时间
Δt1=2arccos[cos8.9574°/cosδs]/ωe
本影时间
Δt2=2arccos[cos8.4240°/cosδs]/ωe
由此对于静止轨道卫星,其地影具有以下特点:
(1) 太阳赤纬绝对值小于8.4240°时,将发生地影。一年中,发生地影的时间大约是从2月27日到4月12日和8月31日到10月16日,全年约92天。
(2) 最长地影时间在δs=0时,即春分和秋分时发生。最长时间约为72min,其中半影时间分为两段,每段时间约为2min。
(3) 卫星定点处的地方真太阳上中天是地影的中点。
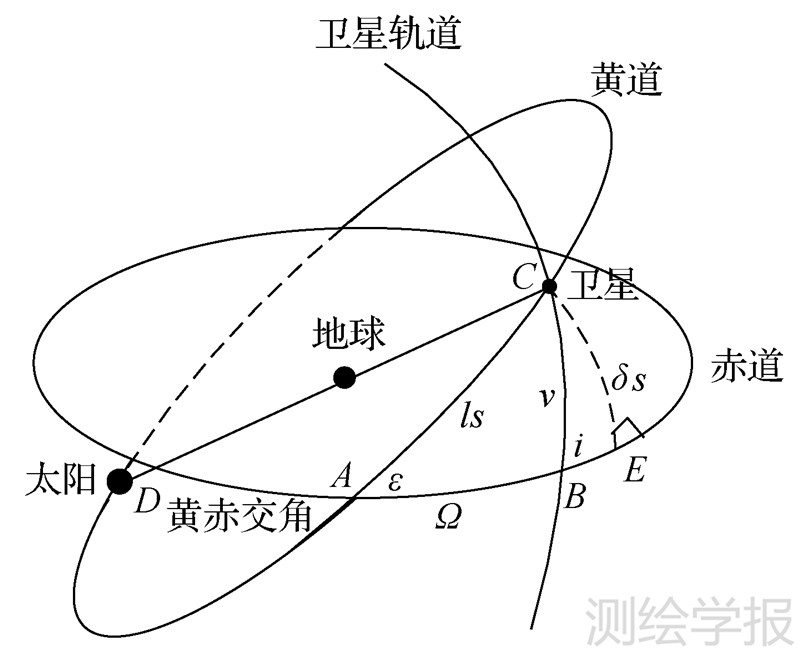
对于IGSO、MEO卫星,设ε、Ω、i分别为黄赤交角、卫星轨道升交点赤经和轨道倾角,由图 5可知,当太阳、地球、卫星位于DC连线,即太阳黄经为180°+ls时发生地影。则在球面三角形ABC中,由四元素公式可得ls(AC)计算公式为
|
| 图 5 球面位置关系图 Fig. 5 Relative spherical position chart |
由此IGSO、MEO卫星地影期与卫星轨道倾角、升交点赤经密切相关。并且与GEO不同,由于平太阳沿黄道以1°/d的速度运动,则ls以度为单位表示时,一年中卫星所经历的两段地影期中的最长地影日分别偏离春分日、秋分日ls天。此外与GEO类似,地影期天数及地影时间还与卫星轨道半长轴相关。
为进一步验证以上结论,并将GEO、IGSO、MEO 3类卫星进行对比,本文以北斗二号卫星导航系统中PRN03(GEO)、PRN06(IGSO)、PRN11(MEO)作为比对研究对象,进行了计算分析。
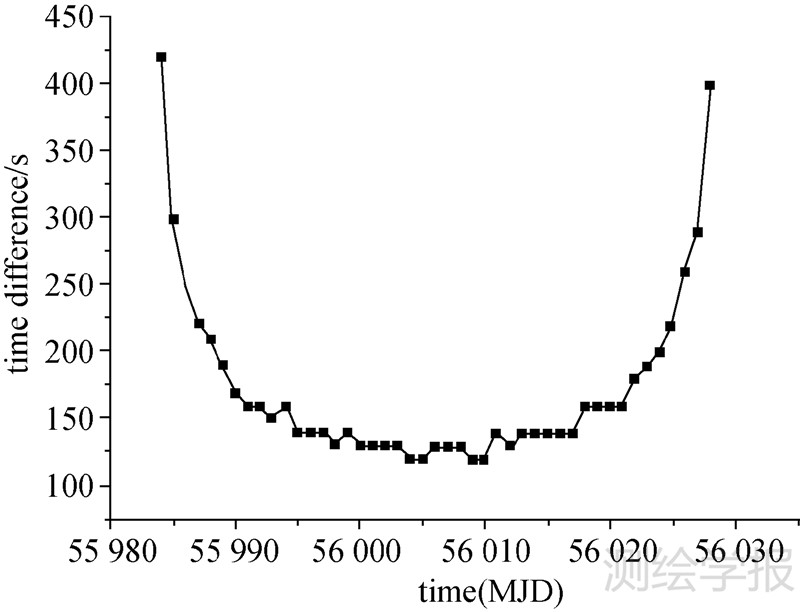
GEO PRN03卫星在2012-02-26—2012-04-14期间共经历46d地影期,数值计算结果与理论公式推导结果一致。在地影期内本影持续时间先增大后减小,在地影期的中部达到最大。最长持续时间为67.5min。图 6为柱形及锥形地影模型计算的卫星本影区时间差异。从图中可以得出:柱形与锥形本影时间差在整个地影期内呈现凹形,最大时间差为420s,最小时间差为120s。这是由于锥形地影模型可以准确表示出半影区,从而与柱形地影相比,卫星进入本影区的时刻相对推后造成的。
|
| 图 6 GEO柱形/锥形各天本影区时间差 Fig. 6 Single day umbra duration difference of GEO satellite using cylindrical and conical shadow model |
IGSO PRN06卫星实测升交点赤经及轨道倾角分别为211.5°、54.7°,由式(1)可得,ls计算值为26.1°。数值计算结果为卫星在2012-04-07— 2012-04-25期间,共经历18d地影期,最长地影日为4月15日,偏离春分日26d,与理论分析结果一致。与GEO相比,IGSO本影区持续时间相对较短,最大持续时间差为290s,最小时间差为120s。
MEO卫星轨道高度较低,以北斗MEO卫星轨道半长轴27906km计算,地球视半径为 13.4584°。MEO PRN11卫星地影持续时间51d。与GEO、IGSO相比,MEO本影区持续时间较短,最长持续时间为55.8min。柱形与锥形地影模型本影区最大持续时间差为180s,最小时间差为60s,也小于GEO、IGSO结果。
由以上分析可知,相对于锥形地影模型,柱形地影模型对3类卫星本影区发生时刻的计算误差是不同的。对于GEO、IGSO、MEO,本影区发生时刻最大计算误差分别达到3.5min、2.4min、1.5min。由此在精度允许的情况下,为减少计算量,MEO卫星可采用柱形地影模型。GEO卫星采用柱形地影模型将承担更大的技术风险,建议谨慎采用。
4 地影状态与轨道根数的关系地影与日、地、卫星三者的相对位置有关。考虑日、地的运动轨迹是天体的自然现象,可以采用行星历表进行计算,在工程实践中其位置也是通过太阳和地球敏感器进行观测的[20]。由此造成不同卫星地影状态差异的因素就主要归结在卫星自身的轨迹(位置)差异[21, 22]。而反映卫星位置的参数可以用坐标XYZ表示,也可以用轨道根数表示。由于轨道根数物理性更强,并通过第3节中3类卫星地影期差异分析可以得出:卫星轨道高度、倾角、升交点赤经是导致不同卫星地影期状态差异的主要因素。因此本节重点针对卫星轨道根数进行分析。与第3节不同,为计算方便,本节以全年两次地影合计持续天数作为统计量进行分析讨论。
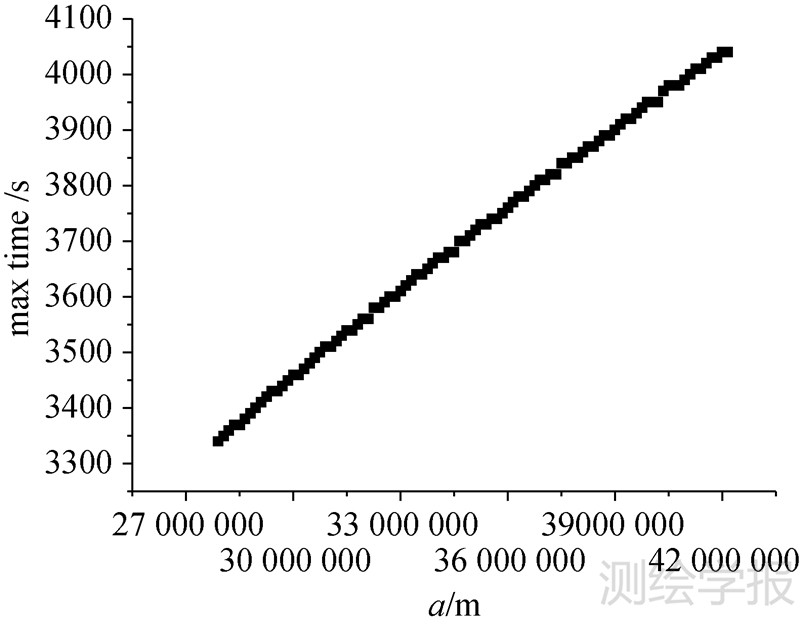
4.1 地影与轨道半长轴的关系假定卫星轨道偏心率、倾角、升交点赤经、近地点幅角分别设定为0、55°、90°、180°,则当卫星轨道半长轴在27906992.7~42164142.1m间变化时,一年内地影持续天数变化情况如图 7。由图中结果,随轨道半长轴的增加,地影持续天数逐渐降低。以GEO卫星轨道半长轴42164km、MEO轨道半径27906km为例,在GEO、MEO处地球圆盘视直径分别为17.3814°、26.3834°,由此较高的轨道半长轴将导致较少的地影天数。但由单天地影最大持续时间变化情况(见图 8)可得,轨道半长轴增大,最大地影持续时间逐渐增加。这主要是由于高轨卫星运动速度较小,由此卫星飘离地影区的时间相对较长。

|
| 图 7 地影持续天数随轨道半长轴变化 Fig. 7 The number of days suffering earth eclipse varies according to semi-major axis |
|
| 图 8 一年内单天最大本影持续时间 Fig. 8 The maximum umbra duration in a year’s time |
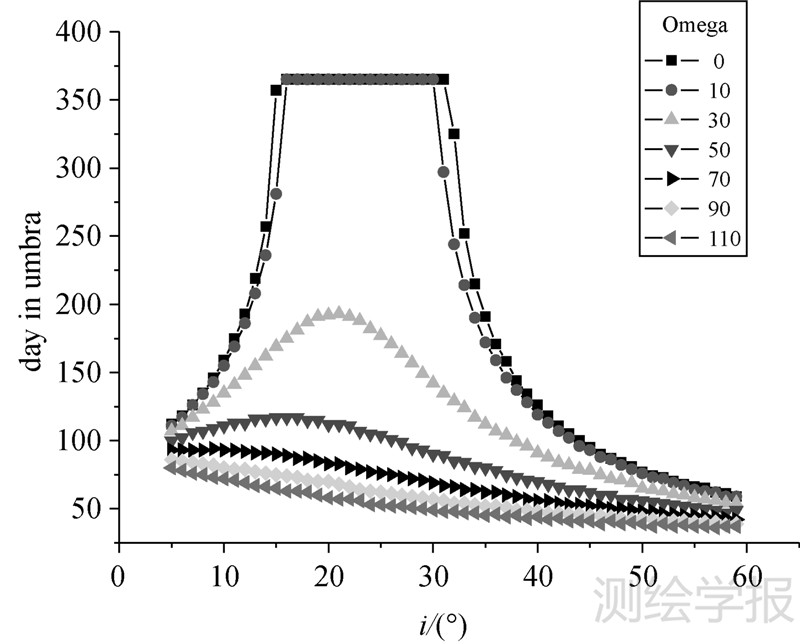
卫星轨道倾角与升交点赤经共同确定了卫星轨道面在空间的位置。以北斗IGSO卫星为例,当升交点赤经在0°~90°间取值,并假设近地点幅角为180°,轨道倾角在0°~60°间变化,卫星地影持续天数变化情况如图 9所示。由图中结果,卫星地影持续天数在轨道倾角23°附近出现峰值,之后随轨道倾角的增大而降低。当升交点赤经逐渐增大时,该现象逐渐消失。
|
| 图 9 地影持续天数随轨道倾角变化 Fig. 9 The number of days suffering earth eclipse varies according to orbit inclination |
分析其原因,以最极端的情况为例,当卫星轨道升交点赤经为0°,即与春分点重合,轨道倾角等于黄赤交角(23°)时,卫星轨道面与黄道面平行,由此卫星一年365天均会经历地影,即当倾角为23°时达到峰值。随着轨道倾角的增大,地影天数逐渐减少,在倾角113°附近达到最低。
地影最大持续时间没有表现出随轨道倾角的变化,各位置均保持不变。地影平均持续时间变化情况如图 10所示,随着升交点赤经的增大,地影平均持续时间趋于平稳。MEO计算结果与此类似。

|
| 图 10 地影平均持续时间随轨道倾角变化 Fig. 10 The mean umbra duration varies according to orbit inclination |
在地影时间与升交点赤经的关系分析中,以北斗IGSO卫星为例,轨道偏心率、近地点幅角分别设定为0°、180°,倾角取0°~180°间的典型值,升交点赤经以10°为间隔在0°~360°间取值。计算结果如图 11所示。

|
| 图 11 地影持续天数随升交点赤经变化 Fig. 11 The number of days suffering earth eclipse varies according to longitude of ascending node |
由图中计算结果,当卫星倾角为0°,即卫星轨道面与赤道面重合时,无论升交点赤经处在什么位置,其与地球、太阳的位置关系均是等价的,因此地影天数相同。当卫星轨道倾角增大时,参见4.2节中的分析结果,卫星会在升交点赤经靠近春分点(0°)附近出现峰值,当升交点赤经为180°时,地影天数达到最少。随着轨道倾角的增大,卫星轨道面与黄道面的关系发生反转,卫星会在升交点赤经靠近秋分点(180°) 时出现峰值。通过分析,卫星单天最长地影持续时间及一年时间内地影平均持续时间没有表现出随升交点赤经变化的情况。
此外,对北斗导航卫星所采用的近圆轨道,偏心率对地影的影响相对较弱。近地点幅角仅反映卫星在轨道面内的相位,并不改变卫星沿其轨道面的周期性运动,其影响可以忽略不计。本文不再进行详细计算分析。
5 结 论(1) 相对锥形地影模型,GEO、IGSO、MEO柱形地影模型本影区发生时刻最大计算误差分别达到3.5min、2.4min、1.5min。建议GEO卫星谨慎采用柱形地影模型。
(2) 对于GEO卫星当太阳赤纬绝对值小于8.4240°时,将经历一年两次的地影期。对于IGSO、MEO卫星,其地影期太阳赤纬中心点位置与轨道倾角、升交点赤经密切相关,最长地影日存在偏离春秋分的现象。
(3) 随轨道半长轴的增加,一年地影持续天数逐渐降低,而平均及最大地影持续时间逐渐增加。
(4) 卫星在升交点赤经靠近春分点(0°)、秋分点(180°)时地影天数存在峰值,并随着轨道倾角的变化,出现最大、最小峰值点反转。
(5) 卫星地影天数在升交点赤经为0°、轨道倾角23°附近出现峰值,之后随轨道倾角的增大而降低。当升交点赤经增大时,该现象逐渐消失。
(6) 对北斗导航卫星,轨道偏心率及近地点幅角对地影状态的影响相对较小。
| [1] | ZHENG Jun,CHEN Hong,LI Yuheng.Algorithm Analysis on Energy System State Switch Time Accurate Prediction in GEO Satellite Eclipse [J].Aerospace Shanghai,2011,28(5):30-33.(郑军,陈宏,李于衡.GEO卫星能源分系统状态切换时间精确预报算法[J].上海航天,2011,28(5):30-33.) |
| [2] | XIA Nanyin,ZHANG Shouxin,MU Hongfei.Space TT&C Systems [M].Beijing:National Defence Industry Press,2002.(夏南银,张守信,穆鸿飞.航天测控系统[M].北京:国防工业出版社,2002.) |
| [3] | YANG Jiachi,FAN Jianfeng.Orbital Dynamics and Control of Spacecraft [M].Beijing:China Astronautic Publishing House,2009.(杨嘉墀,范剑峰.航天器轨道动力学与控制[M].北京:中国宇航出版社,2009.) |
| [4] | Bar-Sever YE.A New Model for GPS Yaw-attitude[J]. Journal of Geodesy,1996(70):714-723. |
| [5] | KOUBA J.A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J].GPS Solution,2009,13(1):1-12. |
| [6] | HAUSCHILD A, STEIGENBERGER P, RODRIGUEZ-SOLANO C. QZS-1 Yaw Attitude Estimation Based on Measurements from the CONGO Network[C]//Proceedings of the 24th International Technical Meeting of The Satellite Division.[S.l.]: Institute of Navigation,2010:1288-1298. |
| [7] | ZHANG Xi,LIU Shimao,LU Benkui.Precise Calculating of Satellite Entry and Exit Times through Umbra/Penumbra[J].Vehicle Control Technology,1995(4):20-25.(张锡,刘世茂,陆本魁.人造地球卫星进出地影时刻的精密计算[J].飞行器控制技术,1995(4):20-25.) |
| [8] | GENG Tao,LIU Jingnan,ZHAO Qile,el at.Compass Precise Orbit Determination Based on Space-ground Monitoring Network[J].Acta Geodaetica et Cartographica Sinica,2011,40(S1):46-51.(耿涛,刘经南,赵齐乐,等.星地监测网下的北斗导航卫星轨道确定[J].测绘学报,2011,40(S1):46-51.) |
| [9] | SHI Chuang,ZHAO Qile,LI Min,el at.Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science of China: Earth Science,2012,42(6):1079-1086.(施闯,赵齐乐,李敏,等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学:地球科学,2012,42(6):854-862.) |
| [10] | LI Min,SHI Chuang,ZHAO Qile,et al.Multi-GNSS Precision Orbit Determination[J].Acta Geodaetica et Cartographica Sinica,2011,40(S1):26-30.(李敏,施闯,赵齐乐,等.多模全球导航卫星系统融合精密定轨[J].测绘学报,2011,40(S1):26-30.) |
| [11] | MA Jianzhen,XUE Shenfang.Two Kinds of The Earth Shadow Models Sunlight Pressure Perturbation Satellite Orbit Comparison[J].Computer Simulation,2008,25(7):46-49.(马建珍,薛申芳.两种地影模型中卫星轨道光压摄动比较[J].计算机仿真,2008,25(7):46-49.) |
| [12] | LI Yuheng,ZHANG Ying,YI Kechu.On Celestial Body Impacts on Geostationary Satellites[J].Flight Dynamics,2005,23(4):79-85.(李于衡,张瑛,易克初.天体对地球同步静止轨道卫星的影响研究[J].飞行力学,2005,23(4):79-85.) |
| [13] | CHEN Liucheng.How Navigation Satellite Orbit Numerical Integration Affected by Shadow Model and Its Correcting Methods[J].Geomatics and Information Science of Wuhan University,2007,32(5):450-453.(陈刘成.地影模型对导航卫星轨道数值积分的影响及改进[J].武汉大学学报:信息科学版,2007,32(5):450-453.) |
| [14] | MULLINS L D.Calculating Satellite Umbra/Penumbra Entry and Exit Positions and Times[J].Journal of the Astronautical Sciences,1991,39:411-422. |
| [15] | OLIVER M,EBERHARD G.Satellite Orbits Models, Methods, and Applications [M].Berlin:Mercedes Druck,2000. |
| [16] | DING Jian,QU Feng,WEI Zhibin,et al.Calculating and Analysis of Satellite Umbra Based on Cartesian Coordinate[J].Science of Surveying and Mapping,2010,35(1):39-41.(丁剑,瞿锋,卫志斌,等.基于笛卡尔坐标的卫星地影模型解析[J].测绘科学,2010,35(1):39-41.) |
| [17] | CHEN Fanfyun,JIA Naihua.Satellite Control Manual[M].Beijing:Science Press,1992.(陈芳允,贾乃华.卫星测控手册[M].北京:科学出版社,1992.) |
| [18] | WANG Jiexian.Precise Orbit Determination and Positioning of GPS[M].Shanghai:Tongji University Press,1997.(王解先.GPS精密定轨定位[M].上海:同济大学出版社,1997.) |
| [19] | GERHARD B, MARKUS R, JAN K. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D].Bern:University of Bern,1999. |
| [20] | LIU Yiwu,CHEN Yiqing.Star-sensor Measurement Model and Its Application to the Spacecraft Attitude Determination System[J].Journal of Astronautics,2003, 24(2):162-167.(刘一武,陈义庆.星敏感器测量模型及其在卫星姿态确定系统中的应用[J].宇航学报,2003, 24(2):162-167.) |
| [21] | ZHANG Shijie,CAO Xibin.Calculating Method of Satellite Entry and Exit Positions and Times through Umbra/Penumbra[J].Aerospace Shanghai,2001(6):9-22.(张世杰,曹喜滨.卫星进/出地影位置和时间的计算算法[J].上海航天,2001(6):19-22.) |
| [22] | ZHENG Jun,BAO Mingtao,WANG Xin,et al.Affection of Longitude Ascending Node and Orbit Inclination on the Eclipse for Geosynchronous Satellite[J].Aerospace Shanghai,2005,22 (3):34-36.(郑军,鲍明涛,王鑫,等.升交点赤经与轨道倾角对地球同步卫星地影的影响[J].上海航天,2005,22 (3):34-36.) |