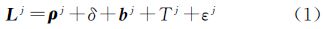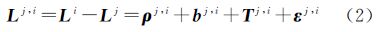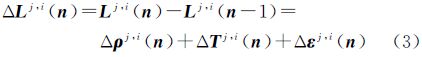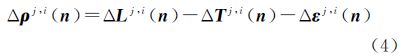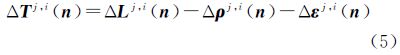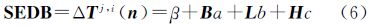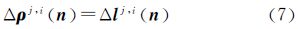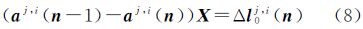2. 中国科学院 上海天文台,上海 200030
2. Shanghai Astronomical Observatory,Chinese Academy of Sciences,Shanghai 200030,China
1 引 言
自从1997年精密单点定位(precise point positioning,PPP)技术被提出以来[1],已在众多领域得到了广泛的应用[2, 3, 4]。常规PPP定位要获得厘米级定位,通常需要30 min以上的时间才能完成初始化,而周跳和失锁等现象所引起的观测数据中断需要同样的重新初始化时间。为了缩短初始化时间并提高PPP定位精度,相关研究人员提出了整周模糊度固定技术[5, 6, 7, 8, 9, 10, 11, 12]。许多专家认为影响参数收敛的因素是非差模糊度参数受接收机和卫星UPD(uncalibrated phase delays)的影响而不具有整数性,致使不能利用其整数特性来固定模糊度[5]。如果采用参考站估计UPD,就可以进行非差模糊度参数整数特性的恢复和固定,实现PPP的快速初始化[5, 13]。也有人采用了历元间差分技术和岭估计理论研究快速PPP定位,只需要两个历元的数据就可以进行PPP解算[14, 15]。虽然使用前几个历元的大气延迟信息可以修复数据中断[16, 17],但当数据间断时间长达几分钟或大气中发生较大的变化时,这一技术仍然会失去作用。因此,进一步缩短初始化时间,达到与网络RTK相同的初始化时间,仍然需要作很多工作。
常规PPP定位中,通常使用无电离层组合观测值,其模糊度可以表示为宽巷和窄巷模糊度,使得组合模糊度的固定变为窄巷和宽巷模糊度的固定。但是,观测噪声放大的宽巷模糊度和波长缩短的窄巷模糊度导致初始化同样需要一个较长的时间。一种进一步缩短初始化时间的有效方法是从CORS参考站提取大气延迟改正数,以减少估计参数的个数,恢复非差模糊度整数特性[18, 19]。本文提出的PPP定位与其他方法最大的区别在于基于星间历元间差分技术消掉模糊度[20],回避模糊度收敛或固定问题,并基于参考站增强信息改善单站用户的PPP定位。
2 基于参考站增强信息的PPP定位 2.1 观测模型假设轨道和卫星钟差的残差可以忽略,则无电离层延迟相位观测可以写为
式中,Lj为第j颗卫星的观测值;ρj为接收机到卫星间的几何距离;δ为接收机钟差;bj为模糊度;Tj 为对流层延迟;εj为观测噪声。星间差分可以得到 式中,上标j、i表示星间差分算子。当相邻历元没有周跳发生时,历元间差分可得到 式中,Δ为历元间差分算子;n为历元。式(3)经整理得到 式(4)为无模糊度观测模型,即星间历元间差分(satellite-differenced and epoch-differenced,SDED)观测方程。式(4)消除了接收机钟差和模糊度参数。 2.2 对流层延迟计算从式(4)可以看出,只要能获取对流层延迟信息,并且能连续跟踪到4颗以上的卫星,就可以进行位置参数的估计。本文拟采用参考站观测,进行用户站对流层延迟改正信息的计算。在区域参考站网络中,参考站的坐标已知,根据式(4)可以进行参考站对流层延迟的计算
在准确得到参考站对流层延迟信息之后可以进行用户站改正信息的计算。式(5)也可以写为
式中,B、L和H分别为参考站对应的经度、纬度和高程;其中a、b和c为参考站位置对应的系数;β是一未知常数;SEDB为星间历元间差分误差(satellite and epoch differenced bias,SEDB),主要为对流层延迟的改正信息。由于在星间历元间差分过程中,对流层延迟采用了模型改正的方法,而对流层模型难以改正的残留误差以及其他潜在误差(人们还没有认知但确实存在的各种系统误差)会给PPP定位产生影响,笔者将这些误差设为SEDB。每个卫星对应的系数和常数可以采用参考站网络数据估计得到。根据SEDB估计策略,对应的流程如图 1所示。

|
| 图 1 SEDB估计流程图 Fig. 1 Flow chart of estimation strategy of SEDB |
图 1给出了SEDB参数估计的流程图,主要包括3个步骤:首先,估计每个参考站每颗卫星对应的SEDB;其次,基于第1步得到的SEDB和每个参考站的位置参数,计算系数a、b、c和β;最后,使用第2步估计得到的系数和用户的近似坐标计算用户站的SEDB。
2.3 用户位置参数的估计在获取用户站的对流层延迟信息之后,通过式(4)就可以估计测站位置参数。将测站的对流层延迟信息带入式(4)后,可以简化为
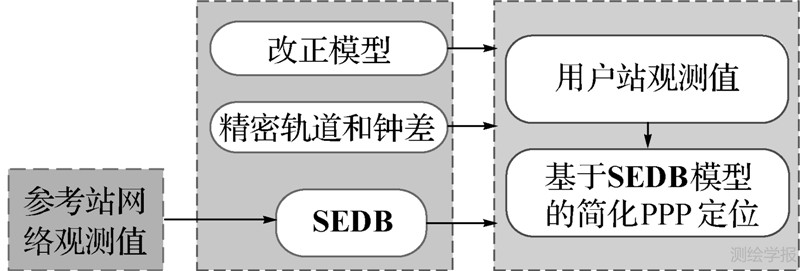
线性化后,可以写为 式中,aj,i(n-1)和aj,i(n)为设计矩阵;X为测站的位置参数。式(8)表明未知参数只有测站坐标。基于上述的SEDB算法,基于参考站增强信息的PPP定位流程如图 2所示。
|
| 图 2 基于参考站增强信息的PPP定位系统流程图 Fig. 2 Flowchart of the reference station augmentation information-based PPP |
图 2给出了基于改正信息SEDB的PPP定位流程图。首先,基于参考站网络进行SEDB估计。使用参考站网络观测值,可以建立卫星对SEDB和测站位置间的关系方程。其次,基于相关方程和用户近似坐标计算用户站SEDB。用户站的近似坐标可用伪距观测值计算得到,并在PPP定位过程中得到修正。基于Melbourne-Wuebbena和无几何组合观测值完成相位数据的预处理,包括周跳探测和粗差剔除。在上述两步骤中,使用了IGS精密轨道和钟差产品。对流层延迟使用Saastamoinen模型进行改正[21, 22]。其他相关的改正模型,诸如相位缠绕、固体潮、相对论效应、天线相位中心偏差和变化等,均使用IERS协议或其推荐方法。估计SEDB和进行PPP定位时使用了高度角加权
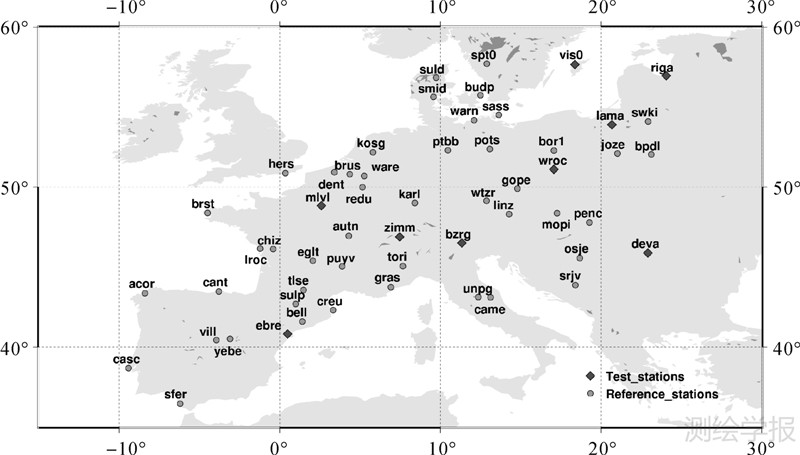
式中,ele是高度角。 3 试验分析基于参考站增强信息的PPP定位方法,处理了欧洲参考框架网络(European reference frame (EUREF) permanent network,EPN)74个参考站的数据。其中67个参考站的单天数据(2009-09-19)用来解算卫星对的SEDB参数,之前已固定参考站坐标、卫星精密轨道和钟差以及EPR数据。其他7个参考站的数据用于评估PPP定位结果,这几个参考站并没有参与SEDB估计。PPP试验以静态模式完成。将这些单天观测值分成96组900 s、72组1200 s和57组1500 s数据。在数据处理过程中,数据采样率设为30 s,高度角设为10°。图 3为选用的EPN参考站,图中圆点所示的参考站用于SEDB估计的参考站;菱形所示的参考站用于PPP定位试验的参考站。
|
| 图 3 EPN参考站网 Fig. 3 Stations selected from EPN and their distribution |
为了分析基于参考站网增强信息的PPP定位效果,分别用常规PPP技术和上述PPP方法处理了不同观测时间的观测值。表 1给出了每个测站到最近参考站的距离和静态PPP定位的成功率(%)。这里的成功率定义为估计坐标与已知参考站坐标的较差小于10 cm的时段与总时段的比值。在表 1中,用户站按距离远近排列,平均距离大约为326.6 km。
| 参考站 | 距离/m | 本文方法/(%) | 常规方法/(%) |
| UNPG | 62.539 | 28 | 3 |
| LAMA | 149.866 | 39 | 0 |
| GOPE | 182.115 | 38 | 0 |
| EBRE | 221.583 | 34 | 0 |
| CASC | 376.399 | 37 | 1 |
| KIRU | 547.023 | 21 | 2 |
| ANKR | 746.655 | 51 | 0 |
| Means | 326.597 | 35.4 | 0.86 |
从表 1中可以看出,即使到参考站的距离达到746 km,基于参考站网增强信息的PPP定位的成功率仍然可以达到51%。与常规PPP比较,当观测时间为900 s时,基于参考站网增强信息的PPP定位的平均成功率可以达到35.4%,而常规PPP定位只有0.86%。就基于参考站网增强信息的PPP而言,虽然SEDBs得到了修正,但是坐标分量的系数矩阵很脆弱难以抵抗较大残差对定位结果的影响。而就常规PPP来说,可以解释为模糊度未完全收敛的结果。
从表 2可以看出,当处理观测时间为1200 s的数据时,基于参考站网增强信息的PPP技术的平均成功率达到了53%,但常规PPP定位的成功率只有1%。与表 1相比,随着观测时间的增加,基于参考站网增强信息的PPP和常规PPP定位的成功率都有所增长,各自的增长率达到了18%和0.14%。
| % | ||
| 参考站 | 本文方法 | 常规方法 |
| UNPG | 53 | 1.4 |
| LAMA | 64 | 1.4 |
| GOPE | 51 | 1.4 |
| EBRE | 48 | 0 |
| CASC | 59 | 2.8 |
| KIRU | 36 | 0 |
| ANKR | 60 | 0 |
| Means | 53 | 1 |
从表 3可以看出,1500 s观测时间的基于参考站网增强信息的PPP定位的成功率均优于56%,常规PPP定位的收敛成功率也达到了1.8%。与1200 s数据相比,它们的平均成功率都有所增长。
| % | ||
| 参考站 | 本文方法 | 常规方法 |
| UNPG | 65 | 1.8 |
| LAMA | 86 | 1.8 |
| GOPE | 70 | 3.6 |
| EBRE | 65 | 5.4 |
| CASC | 79 | 3.6 |
| KIRU | 56 | 8.9 |
| ANKR | 81 | 3.6 |
| Means | 71.7 | 3.8 |
分别用基于参考站网增强信息的PPP方法和常规PPP对观测时间小于1500 s的数据进行处理,并对得到的结果进行了分析。研究结果表明,当使用常规PPP技术时,参数很难在1500 s内收敛,取得较高的定位精度。但笔者提出的基于参考站网增强信息的PPP定位成功率会随着观测数据量的增加而增长,平均成功率可以达到71.7%,而常规PPP定位的成功率却表现得很不理想。相反,当数据处理过程中出现新的模糊度,常规PPP定位的成功率反而会下降,例如,LAMA参考站的1200 s观测数据的成功率为1.45%,而1500 s观测数据的成功率却为0%。
3.2 精度分析从常规PPP定位的成功率可以看出,当处理的数据观测时间小于1500 s时,其参数几乎不能收敛,各坐标分量的定位精度很难达到厘米级。表 4给出了参考站各坐标分量(北、东和高)的静态PPP定位精度(RMS)。比较不同观测时间的定位结果,北方向和东方向的定位精度分别从3.41 cm和5.16 cm提高到了2.58 cm和4.62 cm,但高程方向的精度反而有所下降。高程的精度不高可以解释为虽然使用了SEDB估计,但残差中仍然存在对流层延迟和其他潜在偏差,这部分残差会影响高程的定位精度。
| 参考站 | 距离/km | 900 s/cm | 1200 s/cm | 1500 s/cm | ||||||||
| North | East | Up | North | East | Up | North | East | Up | ||||
| UNPG | 62.539 | 3.92 | 5.27 | 6.83 | 3.10 | 4.73 | 7.48 | 2.54 | 4.91 | 8.70 | ||
| LAMA | 149.866 | 2.95 | 3.85 | 7.41 | 2.43 | 4.95 | 7.38 | 2.61 | 4.31 | 7.49 | ||
| GOPE | 182.115 | 3.20 | 4.97 | 6.76 | 2.68 | 4.94 | 5.80 | 2.43 | 4.59 | 7.20 | ||
| EBRE | 221.583 | 3.87 | 5.53 | 6.50 | 3.67 | 5.48 | 6.32 | 2.26 | 4.60 | 4.98 | ||
| CASC | 376.399 | 3.04 | 5.06 | 5.90 | 2.69 | 5.15 | 7.10 | 2.54 | 5.51 | 5.83 | ||
| KIRU | 547.023 | 3.61 | 6.10 | 7.15 | 2.82 | 4.87 | 8.08 | 3.20 | 4.37 | 8.03 | ||
| ANKR | 746.655 | 3.29 | 5.34 | 4.84 | 2.64 | 4.66 | 4.65 | 2.50 | 4.02 | 4.74 | ||
| Means | 326.597 | 3.41 | 5.16 | 6.48 | 2.86 | 4.97 | 6.69 | 2.58 | 4.62 | 6.71 | ||
使用星间历元间差分技术,可以消除掉模糊度和接收机钟差。为了处理残余的对流层延迟和潜在偏差,又提出SEDB处理方法。基于SDED技术和SEDB方法处理不同观测时间的数据,并与常规PPP定位进行比较,分析了基于参考站网增强信息的PPP定位成功率和精度,得出如下结论:① 观测时间少于1500 s时,常规PPP几乎不能收敛。随着观测数据的累积,常规PPP的成功率有所增加,这说明随着观测数据的累积,非差模糊度解的精度和质量会有所提高;② 随着观测时间的增加,基于参考站网增强的PPP定位成功率也会随之大幅增长;③ 虽然使用SEDB模型对残余的对流层延迟和潜在偏差进行了改正,但仍然存在一些残差,会对高程定位精度产生影响。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. |
| [2] | KOUBA J,HEROUX P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28. |
| [3] | GAO Y, SHEN X. Improving Ambiguity Convergence in Carrier Phase-based Precise Point Positioning [C]. Proceedings of 2001 ION GPS Meeting. Salt Lake City: ION, 2001. |
| [4] | BISNATH S, GAO Y. Current State of Precise Point Positioning and Future Prospects and Limitations[C]//Proceedings of IUGG 24th General Assembly. Perugia: IUGG, 2007. |
| [5] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. |
| [6] | COLLINS P. Isolating and Estimating Undifferenced GPS Integer Ambiguities[C]//Proceedings of the 2008 National Technical Meeting of the Institute of Navigation: 2. Fairfax: ION, 2008: 720-732. |
| [7] | GENG J, MENG X, DODSON A, et al. Integer Ambiguity Resolution in Precise Point Positioning: Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581. |
| [8] | LAURICHESSE D, MERCIER F, BERTHIAS J P. Real Time Precise GPS Constellation Orbits and Clocks Estimation Using Zero-difference Integer Ambiguity Fixing[C]//Proceedings of the 2009 International Technical Meeting of the Institute of Navigation. Anaheim: ION, 2009. |
| [9] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478-483. (张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用 [J]. 测绘学报, 2010, 39(5): 478-483.) |
| [10] | ZHANG Baocheng, OU Jikun. On the Different Strategies for Iterger Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 710-716. (张宝成,欧吉坤. 论精密单点定位整周模糊度解算的不同策略 [J]. 测绘学报, 2011, 40(6): 710-716.) |
| [11] | YI Zhonghai, CHEN Yongqi, ZHU Jianjun, et al. An Approach to Regional Real Time Precise Point Positioning Based on IGS Ultra-rapid Orbit[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 226-231. (易重海,陈永奇,朱建军,等. 一种基于IGS超快星历的区域性实时精密单点定位方法 [J]. 测绘学报, 2011, 40(2): 226-231.) |
| [12] | NIE Jianliang, YANG Yuanxi, WU Fumei. An Algorithm of Dynamic Precise Point Positioning Based on Modified Particle Filtering[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 338-343. (聂建亮, 杨元喜, 吴富梅. 一种基于改进粒子滤波的动态精密单点定位算法 [J]. 测绘学报, 2010, 39(4): 338-343.) |
| [13] | GENG J, TEFERLE F N, SHI C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263-270. |
| [14] | LI H J, CHEN J P, WANG J X, et al. Satellite- and Epoch Differenced Precise Point Positioning Based on Regional Augmentation Network[J]. Sensors, 2012, 12(6): 7518-7528. |
| [15] | LI Haojun, WANG Jiexian, CHEN Junping, et al. The Research on the Fast Static Precise Point Positioning Based on Ridged Estimation [J]. Acta Astronomica Sinica, 2009, 50(4): 438-444. (李浩军, 王解先, 陈俊平, 等. 基于岭估计的快速静态精密单点定位研究[J]. 天文学报, 2009, 50(4): 438-444.) |
| [16] | BANVILLE S, LANGLEY R B. Instantaneous Cycle-slip Correction for Real-time PPP Applications[J]. Navigation, 2010, 57(4): 325-334. |
| [17] | GENG J, MENG X, DODSON A H, et al. Rapid Re-convergences to Ambiguity-fixed Solutions in Precise Point Positioning[J]. Journal of Geodesy, 2010, 84(12): 705-714. |
| [18] | GE M, ZOU X, DICK G, et al. An Alternative Network RTK Approach Based on Undifferenced Observation Corrections[C]//Proceedings of 2010 ION GNSS Symposiums. Portland: ION, 2010. |
| [19] | LI X, ZHANG X,GE M. Regional Reference Network Augmented Precise Point Positioning for Instantaneous Ambiguity Resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158. |
| [20] | HAN S C, KWON J H, JEKELI C. Accurate Absolute GPS Positioning through Satellite Clock Error Estimation[J]. Journal of Geodesy 2001, 75(1): 33-43. |
| [21] | SAASTAMOINEN. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging of Satellites[M]. The Use of Artificial Satellites for Geodesy. Washington: AGU, 1972: 247-251. |
| [22] | JENSEN A B O, OVSTEDAL O. The Effect of Different Tropospheric Models on Precise Point Positioning in Kinematic Mode[J]. Survey Review, 2008, 40(308): 173-187. |