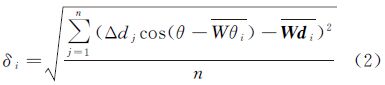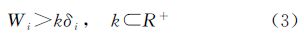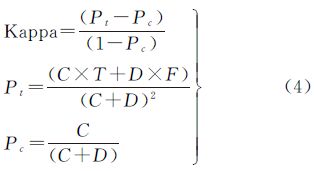1 引 言
影像匹配过程中的误匹配是摄影测量研究领域的一个不可忽视问题。解决误匹配所引入的粗差,即影像匹配粗差,是进行影像定向的关键前提。传统的处理手段一般是通过测量平差技术,在区域网平差解算过程中剔除影像匹配粗差。文献[1, 2]从验后方差估计的角度提出的选权迭代法成为粗差处理的经典算法,在大矩阵解算工程中指导粗差的探测与识别;文献[3]详细论述了相关观测值的抗差估计问题;文献[4]针对粗差探测与识别统计检验量的对比分析,得出基于标准化局部敏感度指标的正态分布更适合于描述粗差表现的结论;文献[5]针对观测值,进行基于偏相关系数和复相关系数的相关分析,可以相对正确地进行多维相关观测的粗差定位。在区域网平差中,影像匹配粗差既是解算过程的自变量,又是因变量,导致平差结果的不确定性。因此,上述算法的处理效果往往与平差解算的稳定性密切联系--区域网平差的网结构较好时,粗差剔除比较可靠,区域网平差的网结构较差时,粗差剔除可靠性失灵 [6, 7]。
传统方法对影像匹配粗差处理具有深刻的指导意义,但匹配粗差的剔除仍旧存在瓶颈。一是实际处理中往往在获取直接观测值,即影像匹配结果后,甚少有其他辅助信息[8, 9];二是在多源数据联合处理的背景下,匹配粗差的探测无法与严格的数学模型一一对应,匹配粗差的剔除难度加大[10, 11];三是在理想情况下,匹配所得到的同名点对应该在整体上满足描述影像关系的数学模型,然而,在摄影成像的瞬间,由于摄影平台、仪器及成像条件的限制,影像之间的关系是十分复杂的,在整体上同名点对大致符合上述数学模型,但在局部仍会出现程度不一的点位偏差,匹配粗差的剔除测度无法从整体考虑而只能从局部考虑[12, 13]。
随着传感器及平台的多样化,高精度影像匹配的技术实现越来越困难,匹配结果中包含大量粗差,无法达到平差处理的最低要求。解决问题的关键在于,根据影像匹配结果,利用统计学规律,避开传统的整体敏感度指标,在平差处理前,进行简单快速的粗差剔除。本文从影像匹配的同名点集合出发,构建局部面元的统计模型,计算面元结构上的点位坐标差矢量,按照正态分布的统计规律,进行粗差剔除。
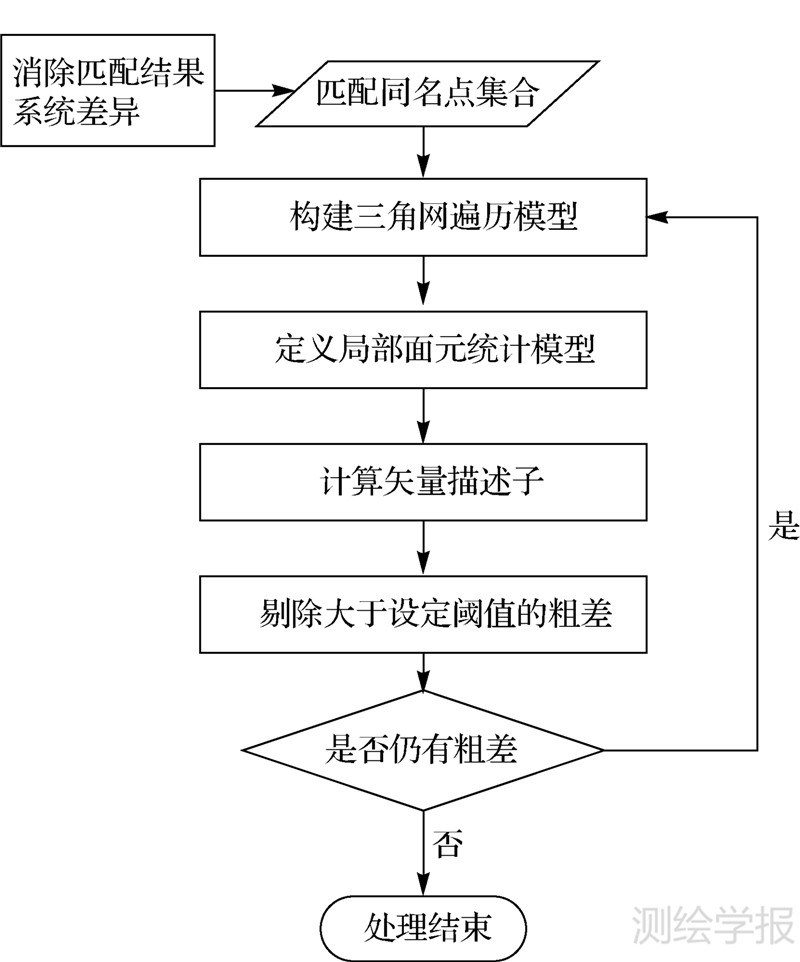
2 算法设计与实现从原始匹配结果出发,影像匹配粗差剔除可以分为以下几个步骤:
(1) 消除物方投影到像方产生的系统性差异。在进行粗差剔除之前,需要对匹配点(对)的差异进行系统修正。这种差异表现为物方投影到不同像方(多张影像)得到的不同投影坐标,其中包含了投影形变及摄站距离,具有整体性。
(2) 利用匹配点集合构建三角网结构,方便匹配点位之间相邻关系的确定。
(3) 实现局部面元统计模型。局部面元是最小的统计单元,其范围内的观测值集合是判定粗差的统计样本。
(4) 计算局部敏感度指标--矢量描述子。矢量描述子由向量W(Δd,θ)构成,包含两个特征值:Δd--影像间同名点坐标差向量的模,θ--坐标差向量与局部标准差向量的夹角(参见第2.2节)。
(5) 根据匹配粗差的判定指标--局部标准差向量描述子,即通过计算与待定点位具有相邻关系的所用匹配同名点对的矢量描述子,求取一个局部范围内的标准差向量,从而达到逐步剔除的目标(参见第2.3节)。由于影像匹配的每一对同名点均为独立匹配,在消除了系统误差之后,匹配误差呈现偶然性,因此符合正态分布的统计规律[14]。
算法流程见图 1。
|
| 图 1 影像匹配粗差的局部矢量面元剔除流程 Fig. 1 The work flow of image matching gross error elimination based on local vector field |
匹配点位在局部范围的统计是设计匹配粗差剔除算法的关键问题。构建匹配点位的二维三角网结构(2D-TIN),实现待定点位的局部面元分割,达到匹配点位的遍历,可以有效解决这一问题。
2D-TIN结构能够很好地描述匹配点对的相邻关系。在2D-TIN结构中,某一个三角形由哪几个匹配点对构成,或者某一匹配点对与哪些匹配点对相邻等空间关系是十分清晰的[15, 16]。这些相邻关系为局部面元的分割提供便利,使得局部几何关系更具有代表性。除此之外,匹配结果决定三角网结构的疏密程度,从一定程度上反映物方空间的地形变化规律与地物特征,这对于局部面元内的观测值统计具有重要意义。
如图 2所示,在三角网结构中,设定待定点位(黑圆点所在位置)附近范围(圆形标记的范围)的所有匹配点位(三角网结构的角点,按照匹配点位的邻接关系选取)作为一个统计单元,则可形成一个多边形的局部面元结构。设定搜索待定点周围两圈的点位作为统计样本,此时,面元的大小根据匹配点位的稠密程度而有所差异,更符合局部自适应的统计规律。
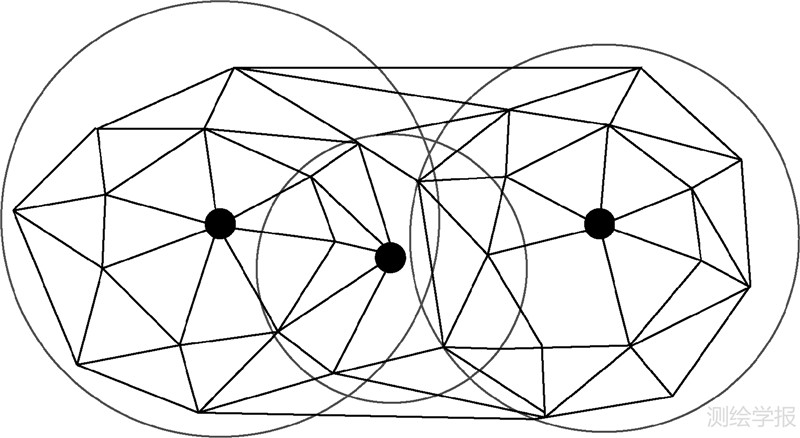
|
| 图 2 局部面元算法实现示意图 Fig. 2 Technical realization of local field |
局部面元具有3个特点:①由于匹配点位的疏密程度不同,局部面元的大小不一;②局部面元内,参与统计的关系点位数量不同;③局部面元构网之后,会对匹配结果有一个粗略的筛选,即极其相近的点位会在构网时自动剔除,保证统计样本中的观测值不存在强耦合性。
2.2 矢量描述子的模型与计算在局部面元内,需要定义能够反映匹配点位真实情况的局部敏感度指标,从而达到探测和剔除匹配粗差的目的。由于大多数匹配结果没有有效的辅助信息,如初始内、外方位元素,单纯从影像匹配的直接观测值出发,矢量描述子作为局部敏感度指标应用性较强。
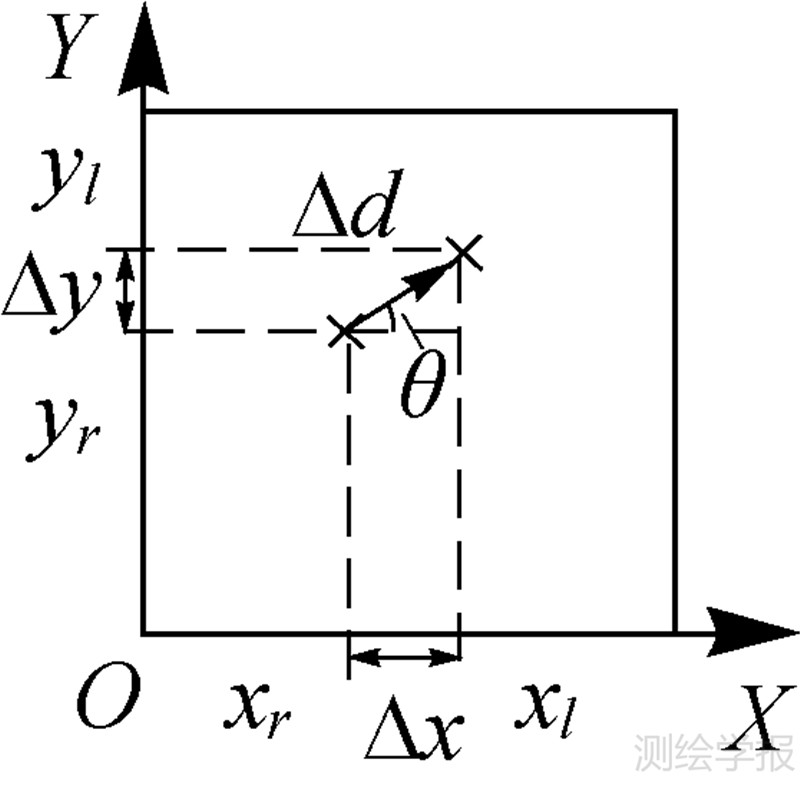
定义W(Δd,θ)为矢量描述子的数学模型。其中,Δd为左、右影像上同名点对的像方坐标差,θ为Δd与x方向的夹角。然而,两幅影像上的同名像点坐标存在差异,如图 3所示。为了消除匹配结果中的系统性差异,首先在左、右影像上量测同名点对al和ar的像方坐标,计算其欧式距离Δd′=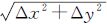 ;然后,针对整体影像上所有点对的Δd取平均值Δd,记Δd=Δd′-Δd。
;然后,针对整体影像上所有点对的Δd取平均值Δd,记Δd=Δd′-Δd。
|
| 图 3 矢量描述子的数学模型 Fig. 3 Mathematical model of vector descriptor |
矢量描述子在局部面元上从两个方面描述影像匹配直接观测值的真实情况:
(1) Δd描述去除系统差异影响后,同名点之间坐标差异的量值。Δd同时包含成像方式(中心投影或线阵扫描)造成的和地形起伏引起的投影偏差。其中,地形起伏引起的投影偏差占主导地位。
(2) θ描述同名点位在左、右像方间的投影差方向。θ表示同名点坐标差值与固定方向形成的角度,理论上代表投影差的方向,其在局部面元上应该具有一致性,能够反映局部面元整体的投影差方向特性。
2.3 阈值选取与粗差判定常规的测量平差处理中以中误差作为衡量精度的指标[17, 18],但在匹配粗差中无法直接使用中误差的一般公式。由于局部敏感度指标定义为矢量描述子的形式,中误差的公式应在局部面元的统计模型中以矢量描述子的形式进行相应变化。
定义局部面元内所有点位的矢量描述子均值为Wdi,其计算公式为式(1),其中Δx、Δy为局部面元内所有参与统计的点位在x方向与y方向坐标差值的均值。需要注意的是,该组均值的计算需要消除左、右影像间的系统性差异(参照第2.2节);定义局部面元内Wθi为均值向量Wdi与像方x方向的夹角。
根据中误差的计算公式,定义矢量描述子的中误差为δi,其计算公式为式(2),其中Δdi为局部面元上某点位矢量描述子的量值,n为局部面元上的统计样本数目。在局部面元上按照式(2)统计关系点位矢量描述子的中误差后,按照式(3)进行粗差判定,其中Wi为某一局部面元内待定点位矢量描述子的量值,kδi为判定指标阈值,若Wi大于阈值,则该待定点位为粗差,予以剔除,若Wi小于阈值,则该待定点位可参与下一次统计处理[19, 20, 21]。其中,k是唯一需要人工干预的参数。通常情况下,设定k为常数2~3。
3 试验与分析 3.1 试验数据本文选用两组影像进行试验,其中第1组是利用资源一号02C卫星平台拍摄的全色影像与多光谱影像数据,覆盖区域为浙江省杭州市与富阳市的部分地区。其中,全色影像的空间分辨率为5 m,多光谱影像的空间分辨率为10 m,影像覆盖范围内包括山区、平地、水域及城区等地形类别,影像匹配方法在这类数据中解决自动化、高精度的数据配准与融合问题。试验中采用物方匹配的方法得到的影像配准同名点数据。第2组是利用无人飞艇平台拍摄的一个测区的数码影像,影像覆盖范围位于江西新余地区,覆盖面积达160 km2,影像具有较大的倾角,影像匹配方法用于解决空中三角量测及立体匹配问题,试验中采用像方匹配的方法得到的影像匹配同名点数据。
由于在大倾角或地形特征复杂的影像上,匹配搜索的拉入范围在局部表现不一致,简单的相关系数匹配会引入数量庞大的匹配粗差,即使采用SIFT算法获得匹配点位预测模型的参数,仍旧无法有效避免误匹配的出现。本文针对两组数据进行影像匹配粗差剔除算法试验,分析算法的适用范围、处理速度及处理效果。
3.2 试验结果及分析第1组试验数据的匹配点位局部示意图如图 4所示,试验中取200像素×200像素的格网进行特征提取,匹配窗口大小为13像素×13像素,搜索窗口大小为51像素×51像素,相关系数阈值为0.85,匹配粗差剔除后,采用人工查看的方式确认剔除点位是否为粗差,剔除点位局部放大图如图 5所示;第2组试验数据的匹配点位示意图如图 6所示,试验中取80像素×80像素的格网进行特征提取,匹配窗口大小为13像素×13像素,搜索窗口大小为31像素×31像素,相关系数阈值为0.8,匹配粗差剔除后,采用人工查看的方式确认剔除点位是否为粗差,剔除点位局部放大图如图 7所示。图 5、图 7中,编号相同的点为匹配得到的同名点。
|
| 图 4 卫星影像匹配结果示意图 Fig. 4 Matching results of satellite image |

|
| 图 5 卫星影像匹配粗差局部放大图 Fig. 5 Gross error in satellite image matching |

|
| 图 6 无人飞艇影像匹配结果示意图 Fig. 6 Matching results of unmanned airship image |

|
| 图 7 无人飞艇影像匹配粗差局部放大图 Fig. 7 Gross error in unmanned airship image matching |
卫星影像匹配试验中,矢量描述子的示意图如图 8所示,其中箭头表示矢量描述子向量,黑色圆圈标记的箭头是在局部表现为粗差的点位。由矢量描述子示意图可以看出,影像在整体上的匹配残差并不具有规律性,但在局部却具有一致的量级和方向。

|
| 图 8 卫星影像匹配矢量描述子分布示意图 Fig. 8 Distribution of vector descriptors in satellite image matching results |
抽取卫星影像数据两个局部面元内的矢量描述子统计分析,结果如表 1所示。表中统计项包括标准矢量描述子、局部面元上的矢量描述子中误差及误差分布情况等统计数据。从统计数据可以看出,在每个局部面元上,标准矢量描述子的模与中误差的大小相当,符合误差统计的规律。同时,匹配点位的残差向量相对于中误差的分布比也满足正态分布的规律,证明统计算法设计的合理性。
| 试验数据 | 标准矢量描述子的模/像素 | 中误差δi/像素 | 匹配点位分布比/(%) | |||
| ≤δi | >δi,≤2δi | >2δi,≤3δi | >3δi | |||
| 局部面元1 | 1.217 | 1.453 | 48.4 | 35.2 | 15.9 | 0.5 |
| 局部面元2 | 0.757 | 0.972 | 52.9 | 32.1 | 14.4 | 0.6 |
两组试验数据的影像匹配粗差剔除结果统计如表 2所示(无人飞艇影像仅抽取其中一个像对进行统计,具体的区域网平差结果如表 3所示)。其中误剔除点指匹配点位正确,但却被错误剔除的点,残余粗差指未被正确剔除的粗差点,正确率=100%×(剔除点数目-误剔除点数目)/剔除点数目。借鉴遥感图像分类的评价体系--Kappa系数,根据式(4)计算评价匹配粗差剔除结果。
式中,C表示剔除点(对)数目;T表示真实粗差(对)数目;D表示残余粗差(对)数目;F表示误剔除点(对)数目。
| 试验数据 | 匹配点/对 | 剔除点/对 | 误剔除点/对 | 残余粗差/对 | 正确率/(%) | Kappa系数 |
| 卫星影像 | 2599 | 35 | 7 | 2 | 80 | 0.757 4 |
| 无人飞艇影像 | 219 | 92 | 12 | 6 | 87 | 0.729 3 |
| 像点中误差/像素 | 像方x方向残差最大值/像素 | 像方y方向残差最大值/像素 | 物方X中误差/m | 物方Y中误差/m | 物方Z中误差/m | |
| 剔除算法加入前 | 7.341 | 125.483 | 97.570 | 7.843 | 2.606 | 1.005 |
| 剔除算法加入后 | 1.128 | 38.500 | 35.673 | 0.115 | 0.117 | 0.384 |
| 注:表3中像方残差最大值是参与平差解算的像点观测值最大粗差 | ||||||
针对资源一号02C卫星的全色影像与多光谱影像的自动化配准与数据融合,由于受到地形起伏、传感器畸变及分辨率等因素的影响,匹配结果往往会出现较多误匹配点。试验结果表明,本文算法能够有效提高两类不同分辨率影像的匹配可靠性,为生产高精度的卫星数据融合产品奠定良好的基础。
针对无人飞艇数据进行区域网平差解算(控制点115个),并在平差解算过程中融入数据探测法、选权迭代法等经典粗差处理方法,对比加入影像匹配粗差剔除算法前后的平差结果,如表 3所示。统计结果表明:尽管平差过程中加入了粗差处理方法,但由于其剔除策略与平差解算参数的强耦合性,以及粗差数量在观测值中所占比例较大的原因,效果并不明显,可见在一般的平差处理中,并不能很好地探测和剔除影像匹配粗差;加入独立的影像匹配粗差剔除算法后,平差结果有了显著的提高,进一步验证了本文算法的有效性和合理性。
对于资源一号02C卫星数据来说,全色传感器与多光谱传感器是同一镜头成像,在几何关系上比较简单,内部畸变与系统误差也相似,匹配结果中只含有少量粗差。从统计数据可以看出,在粗差剔除过程中,算法具有较高的准确性,处理后的匹配结果中基本不含粗差。在单线程处理条件下,试验耗时不超过25 s,证明算法能够满足快速的粗差剔除处理要求。
对于无人飞艇数据来说,由于倾角较大、姿态不稳等原因,影像匹配的结果中存在较多的误匹配点,几乎占到匹配结果的30%~40%,平差结果不理想,无控制的情况甚至可能无法构建平差自由网。从统计数据可以看到,在粗差剔除过程中,算法能够有效地识别绝大多数的点位粗差,剔除正确率较高,处理后的匹配结果只含有极少数的粗差,便于后续的区域网平差处理。在单线程处理条件下,一个像对的剔除耗时不超过15 s,证明算法能够满足快速的粗差剔除处理要求。
4 结 语本文提出的影像匹配粗差剔除算法,利用TIN网结构实现了匹配点位的局部面元遍历,计算并统计与待定点位具有相邻关系的匹配点位的矢量描述子,从而有效完成匹配粗差检测与剔除。该算法避开大规模平差运算的影像匹配粗差剔除算法,能够进一步推动数字摄影测量生产流程的自动化。试验证明,该方法处理速度快、剔除成功率高,不仅能够解决实际的生产作业问题,而且能为摄影测量误差处理与可靠性理论的研究提供新的视点。
匹配粗差剔除算法与影像匹配算法相结合,粗差判定测度与统计指标设计等问题将是影像匹配粗差剔除算法新的研究重点。
| [1] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002: 240-255.(李德仁,袁修孝.误差处理与可靠性理论[M].武汉:武汉大学出版社,2002: 240-255.) |
| [2] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722. (陈义,陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.) |
| [3] | YANG Yuanxi. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99. (杨元喜.大地测量相关观测抗差估计理论[J].测绘学报,2002, 31(2): 95-99.) |
| [4] | GUO Jianfeng, ZHAO Jun. Comparative Analysis of Statistical Tests Used for Detection and Identification of Outliers[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 14-18. (郭建锋,赵俊. 粗差探测与识别统计检验量的比较分析[J]. 测绘学报,2012,41(1): 14-18.) |
| [5] | TAO Benzao, YAO Yibin, SHI Chuang. Distinguishability of Outlier Based on Correlative Analysis[J]. Geomatics and Information Science of Wuhan University, 2004, 29(10): 881-884. (陶本藻,姚宜斌,施闯. 基于相关分析的粗差可区分性[J]. 武汉大学学报: 信息科学版, 2004, 29(10): 881-884.) |
| [6] | ZHANG Yongjun, XIONG Jinxin, HAO Lijuan. Photogrammetric Processing of Low-altitude Images Acquired by Unpiloted Aerial Vehicles[J]. The Photogrammetric Record, 2011, 26(134): 190-211. |
| [7] | ZHANG Zuxun. From Digital Photogrammetry Workstation(DPW) to Digital Photogrammetry Grid(DPGrid)[J]. Geomatics and Information Science of Wuhan University,2007, 32(7): 565-570. (张祖勋. 从数字摄影测量工作站(DPW)到数字摄影测量网格(DPGrid)[J]. 武汉大学学报: 信息科学版, 2007, 32(7): 565-570.) |
| [8] | ZHANG Zuxun. Digital Photogrammetry and Computer Vision[J]. Geomatics and Information Science of Wuhan University,2004, 29(10): 1035-1039. (张祖勋.数字摄影测量与计算机视觉[J]. 武汉大学学报: 信息科学版, 2004, 29(12): 1035-1039.) |
| [9] | ZHANG Zuxun. Integration of Photogrammetry and Engineering Surveying[J]. Geospatial Information,2004, 2(6): 1-4. (张祖勋. 论摄影测量与工程测量的结合[J]. 地理空间信息,2004,2(6): 1-4.) |
| [10] | GRUEN A. Development and Status of Image Matching in Photogrammetry[J]. The Photogrammetry Record, 2012, 27(137): 36-57. |
| [11] | GRUEN A, AKCA D. Least Squares 3D Surface and Curve Matching[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2005, 59(3): 151-174. |
| [12] | SCHREIER H W, BRAASCH J R, SUTTON M A. Systematic Errors in Digital Image Correlation Caused by Intensity Interpolation[J]. Optical Engineering, 2000, 39(11): 2915-2921. |
| [13] | CHENG Xiaojun, HU Minjie. The Determination of Digital Camera’s Distortion[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2):113-117. (程效军, 胡敏捷. 数字相机畸变差的检测[J]. 测绘学报, 2002, 31(2): 113-117.) |
| [14] | FENG Haojian. Generalized Normal Distribution and Combined Adjustment Method[J]. Acta Geodaetica et Cartographica Sinica, 1983, 12(3): 223-230. (冯浩鉴. 广义正态分布与综合平差法[J]. 测绘学报, 1983, 12(3): 223-230.) |
| [15] | SHAO Chunli, HU Peng, HUANG Chengyi, et al. The Expatiation of Delaunay Algorithms and a Promising Direction in Application[J]. Science of Surveying and Mapping, 2004, 29(6): 68-71. (邵春丽, 胡鹏, 黄承义, 等. Delaunay三角网的算法详述及其应用发展前景[J]. 测绘科学, 2004, 29(6): 68-71.) |
| [16] | WU Xiaobo, WANG Shixin, XIAO Chunsheng. A New Study of Delaunay Triangulation Creation[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 28-35. (武晓波, 王世新, 肖春生. Delaunay 三角网的生成算法研究[J]. 测绘学报, 1999, 28(1): 28-35.) |
| [17] | PETER J H. Robust Statistics[M]. Hoboken: John Wiley &Sons, 1981. |
| [18] | Survey Adjustment Subject Group of Wuhan University. Error Theory and Measurement Adjustment Basis[M]. Wuhan: Wuhan University Press, 2006. (武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社,2006.) |
| [19] | SCHAFFRIN B. A Note on Constrained Total Least-squares Estimation[J]. Linear Algebra and Its Applications, 2006(417): 245-258. |
| [20] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [21] | NEITZEL F. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |