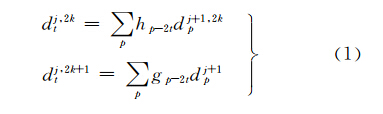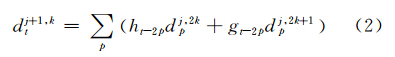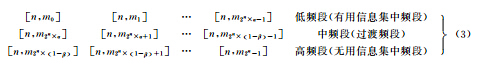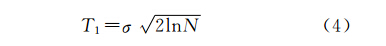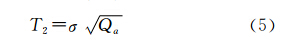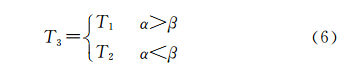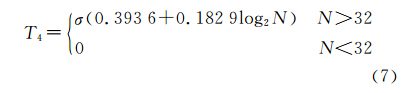1 引 言
小波分析因其具有良好的时频特性,已被广泛应用于形变分析中,并取得了不错的效果[1]。例如对高层建筑的动态监测[2, 3],矿层的移动分析[4]以及大坝的变形预报[5]等。但小波分析主要是提取低频有用信息,容易忽略中频以及高频有用信息,这会对高精度GPS变形监测的分析结果产生不良影响。例如对高层建筑进行变形监测,不仅要监测出其主模态的振动频率,有时还需提取其风致振动变形、台风暴雨等极端天气引起的变形信息,这些变形信息的振动频率已高达甚至超过10-1 Hz[6],当采样频率较低时传统的小波分析就容易产生过度去噪的现象,无法准确提取有用信息。小波包分析是一种新的小波分析方法,具有更好的去噪能力,它不仅像小波分析一样对观测数据的低频部分进行分解,还能对观测数据的高频部分进行分解,能相对有效地提取各频段的有用信息[7]。目前,小波包分析已在数据去噪[8]、振动信息提取[9]等变形监测领域广泛应用。其中小波包应用的关键是对小波包分解系数选取合适的阈值准则并进行阈值处理,现今已有了诸如改进的单阈值处理[10]和普通的多阈值处理[11, 12]的方法,较传统小波包去噪的效果有一定改善,但是上述方法并没有完全充分考虑信号及其噪声的分布,去噪精度有待进一步提高。
如何对小波包分解系数排序重组并进行多阈值处理是高精度去噪的关键问题。文献[11]的方法是对小波包树的第一个节点和最后一个节点进行了特殊化处理,虽然提高了去噪精度,但是事实上最后一个节点并不是频率最高部分,如果不按照小波包树节点的频率顺序,而利用小波包树分解的自然顺序进行多阈值处理,虽然能够对高频部分的噪声进行相对有效地处理,但却是一种比较粗糙的多阈值处理方法。文献[12]的方法是依据小波包分解系数的能量来进行分组,同样提高了去噪精度,并且比文献[11]的方法更为精确,但是当各个频段中噪声污染不稳定时,即噪声污染比较复杂,已严重影响了信号的能量分布,这时候根据能量来进行分组会对有用信息的提取造成困难。
基于这些问题,本文提出了一种小波包去噪方法,即根据不同信号及其噪声的分布,对小波包分解系数按照频率大小的顺序进行排列,依据信息类型分段,对每个频段选取合适的阈值准则并进行阈值处理。它是一种基于频率顺序的多阈值准则(the multi-threshold criteria based on frequency order)小波包去噪法,称为FMC法。理论和实例证明,该方法去噪能力优于传统方法,并且能够有效提取信号中各频段的有用信息,可以高效处理变形监测数据。
2 小波包多阈值去噪法的关键技术
2.1 小波包分解系数的排序重组
小波包理论的分解算法和重构算法的数学表达式如下[9]。
小波包的分解算法是通过dj+1,kt求dj,2kt以及dj,2k+1t实现
小波包的重构算法是通过dj,2kt以及dj,2k+1t求dj+1,kt实现
式中,h、g为滤波器系数;d为小波包分解系数;p、t为分解层数;j、k为小波包节点号。
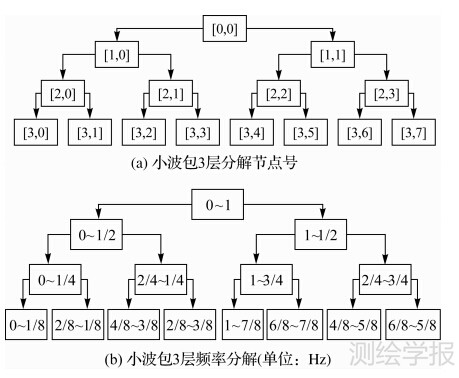
由于噪声在频率域上的分布主要集中在频率较高的部分[13, 14]。因此在利用小波包去噪时,假如不同频段信息采用同一种阈值处理方法,或者同一个频段信息采用不同阈值处理方法势必会影响去噪精度。因此如何准确划分频段是进行多阈值去噪的关键问题。这里提出了一种按照频率大小顺序排列,并依据信息类型重组的划分方法。根据小波包变换理论,它可以将隐含在低频、中频、高频中的有用信息提取出来,以分3层为例,信号分解如图 1(a)所示。以采样频率为2Hz的GPS变形监测数据为例,同时根据那奎斯特(Nyquist)采样定理,将信号用小波包分解如图 1(b)所示。然后再将第3层每一个小波包树节点与图 1(a)进行逐一对应,得表 1。
|
| 图 1 小波包3层分解节点号及频率分解示意图 Fig. 1 Three layers of decomposition node numbers and frequency decompositions with wavelet packet |
通过表 1可以发现,小波包树节点的自然顺序与频率顺序存在不一致现象。最低频部分对应的是第1个节点,最高频部分对应的是第5个节点。出现这种现象的原因是由于小波包分解时,高通滤波器会进行一次“翻转”操作。可以通过小波包的性质证明,任何小波包的分解都会产生自然顺序与频率顺序不一致的现象,并且不一致的现象的情况是一样的[15]。因此,小波包每分解一层时,低频分解部分按频率从小到大排列,高频部分按频率从大到小排列。在变形监测领域,因为噪声分布和频率顺序紧密相关,因此需要的是频率顺序而不是自然顺序。
在形变分析中,往往有需要集中保留的频段以及集中去噪的频段。例如图 1(b)情况的分解,如果需要监测0.15 Hz的建筑物主模态振动频率信息,根据计算,[3, 0]、[3, 1]为有用信息集中频段,即为低频段;而噪声污染情况一般,[3, 4]为无用信息集中频段,即为高频段;其余节点为过渡频段,即为中频段。因此,可以根据需要监测的频段以及噪声污染情况,对小波包分解系数进行分组,即为依据信息类型重组的方法。
具体而言,根据信号及其噪声的分布,以分3层为例,设α为低频段比例系数,β为高频段比例系数,n为信号分解层数。则有小波包树节点分组如(3)所示。需要指出的是,在某些特殊情况下,也可以对频段进一步细分,分为低频、次低频、中频、次高频以及高频,但基本原理不变。
式中,小波包树节点[n,m0]、[n,m1]、…、[n,m2n-1]按频率顺序从小到大进行排列。2.2 小波包分解系数的多阈值处理
单一阈值准则由于没有充分考虑信号及其噪声的分布,因此去噪时很容易出现去噪效果不明显或是去噪过度等现象,而多阈值准则就很好地克服了上述缺点。多阈值准则的基本思想就是根据一定法则,对每个小波包分解系数灵活的选用不同阈值准则,从而最大程度地保留有用信息,去掉无用信息。小波包分析中常用的四种阈值准则包括固定形式阈值准则 (sqtwolog)、自适应阈值准则(rigrsure)、启发式阈值准则(heursure)以及极小化极大阈值准则(minimaxi)[16],由于各自的选取规则不一,去噪效果不尽相同。因此, 每一个小波包分解系数都有它最合适的阈值准则。
(1) 固定形式阈值准则。它所采用的是固定形式的阈值,其公式为
式中,σ为噪声信号的标准差;N为信号长度。
(2) 自适应阈值准则。它是基于 Stein 的无偏似然估计原理的一种阈值,其公式为
式中,σ为噪声信号的标准差;Qa为依据无偏似然估计原理而得到的小波包分解系数的平方。
(3) 启发式阈值准则。它是一种无偏风险阈值,是前两种阈值准则的综合,选取规则为
式中,α=W-N/N;β=3/2 log 2NN;W为N个分解系数的平方和。
(4) 极小化极大阈值准则。也是一种固定形式的阈值,是在最坏条件下求最大均方误差的最小值,这在统计学上叫做“悲观法”,选取规则为
式中,σ为噪声信号的标准差;N为信号长度。
4种阈值准则都有其各自特点。其中,sqtwolog阈值准则以及heursure阈值准则两种方法类似,都是将全部系数进行了处理[17, 18],因此可以较强地去除噪声,与之相对应的,容易过度去噪,因而可以称之为“激进”的去噪准则,适合处理GPS信号的高频部分。rigrsure阈值准则以及minimaxi阈值准则是将部分系数进行了处理[17, 18],是一种较为折中的处理方法,因此,它可以防止过度去噪,与之相对应的容易出现去噪不明显的现象,因而可以称之为“保守”的去噪准则,适合处理低频部分。其中,中频段更适合采用rigrsure阈值准则以及minimaxi阈值准则[11, 15, 19]。
为此,建立如表 2所示的多阈值准则选取表,以用于对小波包分解系数的阈值处理。
| 低频段 | 中频段 | 高频段 |
| rigrsure | rigrsure | sqtwolog |
| minimaxi | minimaxi | heursure |
基于频率顺序并依据信息类型进行分段的小波包多阈值准则处理方法是一种精度较高的去噪方法。下面给出其算法步骤,以分高中低3个频段为例。
(1) 小波包分解。根据所给信号选定一个合适的小波基函数 以及决定所需的分解层次n,对信号进行小波包分解,得到小波包树。
(2) 优化小波包树(可选)。确定熵标准从而选定最优小波基,得到最优树。
(3)根据信号及其噪声的分布,选定低频段比例系数α和高频段比例系数β。其中,有用信息集中的频段越多,α越大;无用信息集中的频段越多,β越大。通过排序重组,得到各频段的小波包树节点信息。
(4) 根据表 2的选取标准,决定低频段阈值准则A、中频段阈值准则B、高频段阈值准则C,对各频段的小波包分解系数分别进行阈值处理。
(5) 小波包重构。对处理后的小波包分解系数进行小波包重构,最终得到去噪信号。
3 仿真试验
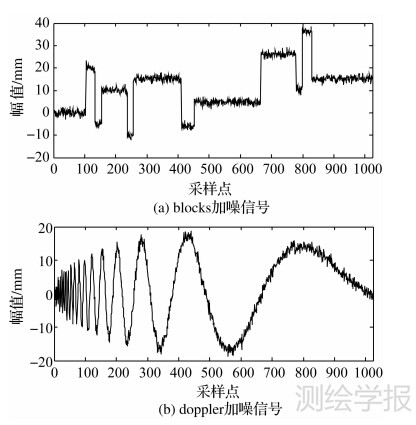
为了验证此法的有效性和优越性,进行了一系列的对比分析。以Matlab为平台,使用评价小波去噪效果质量的两种专用测试信号:blocks信号和doppler信号,在这些信号上加上高斯白噪声,信噪比为10 dB,信号长度为1024个采样点,采样频率为1 Hz。这两种信号都为非平稳信号,前者具有突变性,后者具有渐变性,因此基本涵盖了变形监测数据的特点。其加噪信号如图 2所示。选用均方根误差(RMSE)、信噪比(SNR)以及与真实信号的相关系数( r )为评价指标[20],用来定量比较去噪效果,其中均方根误差越小、信噪比越大、相关系数越高则去噪效果越好。
|
| 图 2 两种加噪信号 Fig. 2 Two noisy signals |
为了较为全面地认识基于频率顺序的多阈值准则(FMC)小波包去噪法的去噪效果,将上述测试信号分别用小波通用去噪,小波包强制去噪,小波包单一全局阈值准则去噪(sqtwolog,rigrsure,heursure,minimaxi),文献[11]的方法以及FMC法进行处理,每种方法得到对应的RMSE、SNR以及 r 。上述各方法若涉及选取小波基的,均使用工程实际中被广泛应用的db4小波基,db4小波基具有正交性,可以任意分解,另外还有保证高频信息不丢失的高度紧支撑性[21]。根据信噪比,分解层数定为3层。涉及阈值类型的选取时都采用软阈值,这样可以更好地保护有用信息。参数的统一还可以保证去噪效果仅与分解方法(小波与小波包)、阈值准则以及频率顺序有关。使用小波通用去噪的目的是作为一个基准,因为此法具有简单、快速、稳定的特点,在实际工程应用中被广泛使用。使用小波包强制去噪的目的是为了比较没有带阈值准则的处理与带阈值准则的处理的差别。分别利用4种阈值准则进行小波包单一全局阈值准则去噪是为了比较单一阈值准则的处理与多阈值准则的处理的差别。使用文献[11]的方法去噪是为了验证基于频率顺序并依据信息类型排序重组的有效性,其中,节点[3, 0]采用minimaxi准则,节点[3, 7]采用sqtwolog准则,其余节点采用rigrsure准则。
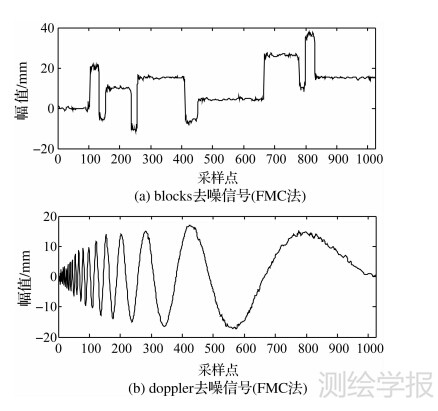
图 3是利用FMC法对两种加噪信号进行去噪的结果。具体过程如下:选定db4为小波基函数,分解层数为3,对信号进行小波包分解,得到小波包树;熵标准定为Shannon,优化小波基,得到最优树;根据信号及其噪声的分布,设低频段比例系数 α=1/8,高频段比例系数β=1/8,重组小波包树节点,具体而言,低频段节点为[3, 0],高频段节点为[3, 4],其余节点分在中频段;依据表 2,选低频段阈值准则A 为minimaxi、中频段阈值准则 B 为rigrsure、高频段阈值准则 C 为sqtwolog,分别对小波包树节点系数进行阈值处理,具体而言,节点[3, 0]采用minimaxi准则,节点[3, 4]采用sqtwolog准则的,其余节点采用rigrsure准则;对处理后的小波包分解系数进行小波包重构,得到去噪信号。
|
| 图 3 两种去噪信号(FMC法) Fig. 3 Two de-noising signals (FMC) |
将各种去噪方法后得到的信号的均方根误差、信噪比以及相关系数列表如表 3所示。
| 方法 | blocks信号 | doppler信号 | |||||
| RMSE /mm | SNR /dB | r | RMSE /mm | SNR /dB | r | ||
| 小波通用去噪 | 1.0236 | 23.3114 | 0.9948 | 0.8140 | 21.9036 | 0.9967 | |
| 小波包强制去噪 | 1.8606 | 18.1210 | 0.9825 | 1.2521 | 18.1630 | 0.9921 | |
| 小波包sqtwolog准则去噪 | 0.9865 | 23.6325 | 0.9951 | 0.7755 | 22.3240 | 0.9970 | |
| 小波包rigrsure准则去噪 | 0.8195 | 25.2427 | 0.9967 | 0.7654 | 22.4374 | 0.9971 | |
| 小波包heursure准则去噪 | 0.9601 | 23.8676 | 0.9954 | 0.7743 | 22.3373 | 0.9970 | |
| 小波包minimaxi准则去噪 | 0.8701 | 24.7231 | 0.9962 | 0.7623 | 22.4733 | 0.9971 | |
| 文献[11]的方法 | 0.7955 | 25.5010 | 0.9968 | 0.5628 | 25.1085 | 0.9984 | |
| FMC法 | 0.7607 | 25.8903 | 0.9971 | 0.5464 | 25.3662 | 0.9985 | |
由表 3可知,FMC法去噪后的均方根误差最小,信噪比最大,相关系数最高,因此去噪效果最好。通过分析可以得到以下几点结论:所有方法都可以不同程度地去噪,因此可以应用于GPS变形监测领域;去噪效果最差的是小波包强制去噪,原因是因为没有利用到阈值准则,这在调整系数时,会产生很多误差,因此必要的阈值准则是提高去噪效果的有效方法;小波包单一全局阈值准则去噪效果优于小波通用去噪,说明小波包去噪的精度整体上是优于小波去噪的;4种阈值准则的去噪效果相当,对于不同信号,各有优劣,如何正确认识信号以及阈值准则的特点并灵活使用,是一个值得注意的问题;FMC法和文献[11]的方法去噪效果优于小波包单一全局阈值准则去噪,说明多阈值准则处理能够提高去噪精度;FMC法去噪效果优于文献[11]的方法,证明基于频率顺序并依据信息类型排序重组可以切实提高精度。
4 工程实例
为了验证该法在实际工程中的去噪效果,进行了一组试验。数据是从某教学楼顶连续观测所得的GPS数据,基线长度约为13m,数据采样率为1Hz,连续观测7d,经双差解算、多路径重复性周期对齐之后等预处理而得到 y 方向的坐标残差数据。这7d数据具有高度相关性,其中存在着多路径效应、建筑物主模态的振动频率,以及风致振动变形等信息,所有这些有用信息的振动频率达到10-1 Hz数量级。
利用FMC法对该GPS变形监测数据进行去噪。根据原始信号特点,选定具有正交性以及保证高频信息不丢失的高度紧支撑性的db4为小波基函数,熵标准定为shannon;根据小波包分解性质以及那奎斯特采样定理,采样频率为1Hz,所需要的小波包分解系数分辨率为0.01Hz,分解层数为5时分辨率为0.015625Hz,符合要求,确定分解层数为5;根据原理,0.015625为每一个小波包分解系数的频段大小,而有用信息高达10-1 Hz,因此低频段和中频段的分界点为0.1Hz,即低频段比例系数 α=8/32,又噪声污染情况一般,即高频段比例系数β =4/32;依据表 2,选定阈值准则 A 为minimaxi、 B 为rigrsure、 C 为sqtwolog。具体而言,节点[5, 0]、[5, 1]、[5, 3]、[5, 2]、[5, 7]、[5, 6]、[5, 4]、[5, 5]采用minimaxi准则,节点[5, 23]、[5, 22],[5, 20]、[5, 21]采用sqtwolog准则,其余节点采用rigrsure准则。以第1天为例,原始信号和去噪信号如图 4所示,从结果可以看出去噪后信号的噪声得到了有效剔除。

|
| 图 4 第1天的原始信号及其去噪信号 Fig. 4 The first day of original signal and de-noising signal |
此外,还使用小波通用去噪、文献[11]的方法对该数据进行了去噪。并计算了第一天与后面各天坐标残差间的原始相关系数与各种方法得到的新的相关系数 r ,如表 4所示;表 5同时计算了各天坐标残差的标准偏差。通过分析能够发现,所有经去噪后的信号中,FMC法处理后的相关系数提高最明显,标准偏差最小,由此最大程度地去除了噪声的污染,去噪效果最好。
| 处理方式 | 1~2d | 1~3d | 1~4d | 1~5d | 1~6d | 1~7d |
| 未处理 | 0.8267 | 0.8294 | 0.7977 | 0.7605 | 0.7099 | 0.7123 |
| 小波通用去噪 | 0.8618 | 0.8705 | 0.8433 | 0.8045 | 0.7537 | 0.7563 |
| 文献[11]的方法 | 0.8714 | 0.8791 | 0.8532 | 0.8163 | 0.7656 | 0.7681 |
| FMC法 | 0.8755 | 0.8841 | 0.8574 | 0.8181 | 0.7668 | 0.7692 |
| 处理方式 | 1d | 2d | 3d | 4d | 5d | 6d | 7d |
| 未处理 | 4.7440 | 4.1156 | 4.1348 | 4.0017 | 3.9006 | 3.6200 | 3.6945 |
| 小波通用去噪 | 4.6433 | 4.0056 | 4.0287 | 3.8846 | 3.7912 | 3.5045 | 3.5801 |
| 文献[11]的方法 | 4.6000 | 3.9630 | 3.9890 | 3.8404 | 3.7370 | 3.4502 | 3.5244 |
| FMC法 | 4.5867 | 3.9401 | 3.9662 | 3.8210 | 3.7290 | 3.4452 | 3.5198 |
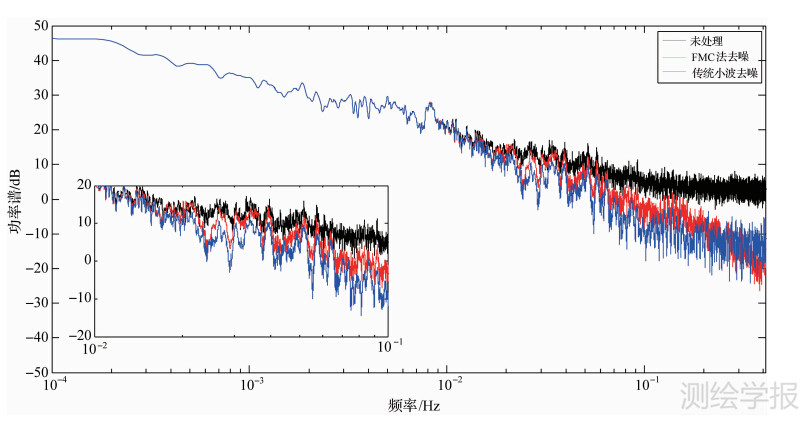
为更直观地说明本方法去噪效果好的原理,图 5给出了利用welch平均周期图法得到的原始信号、FMC法去噪信号以及传统小波去噪信号的功率谱密度估计图。由图 5能够看出,两种去噪信号的功率谱密度在10-2 Hz以下的信息都得到了很好的保留,已基本满足去噪需要;而在大于10-1 Hz的信息部分,FMC法的去噪之后的功率谱从形状以及减弱情况来看也比小波去噪要好。通过图 5放大图可以发现,在高精度GPS变形监测所需要保留的10-2~10-1 Hz的信息,传统小波去噪之后的功率谱密度与原信号的功率谱密度相差较大,而FMC法则更接近原信号,保留了有用信息。因此,在高精度GPS变形监测中,FMC法去噪能够防止去噪不明显或去噪过度等现象,是一种稳定的去噪方法。
|
| 图 5 功率谱密度图 Fig. 5 Power spectrum density |
5 结 论
通过试验分析与工程应用,可以发现本文方法去噪效果优于传统的小波、小波包去噪方法以及其他改进的小波包去噪方法。本文的创新点如下:① 传统小波、小波包去噪并没有充分考虑信号及其噪声的分布,而基于频率顺序并依据信息类型划分的多阈值准则处理方法,可以在剔除噪声的同时有效保护各频段的有用信息;② 基于频率顺序并依据信息类型划分的观点用于小波去噪,这为小波、小波包的多阈值准则去噪提供了一种思路。
| [1] | HUANG Shengxiang, LIU Jingnan. A Novel Method for Reducing Noises in GPS Deformation Monitoring System[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 104-107.(黄声享,刘经南. GPS变形监测系统中消除噪声的一种有效方法[J]. 测绘学报,2002,31(2):104-107.) |
| [2] | HUANG Shengxiang, LIU Jingnan, LIU Xianglin. Deformation Analysis Based on Wavelet and Its Application in Dynamic Monitoring for High-rise Buildings[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 153-157.(黄声享,刘经南,柳响林. 小波分析在高层建筑动态监测中的应用[J]. 测绘学报,2003,32(2):153-157.) |
| [3] | KUANG Cuilin, DAI Wujiao. Measurement of Wind-induced Vipation of Tall Buildings Using GPS and Wavelet Application[J]. Geomatics and Information Science of Wuhan University, 2010, 35(9): 1024-1028.(匡翠林,戴吾蛟. GPS监测高层建筑风致振动变形及小波应用[J]. 武汉大学学报:信息科学版,2010,35(9):1024-1028.) |
| [4] | GU Qinghua, LU Caiwu, GUO Jinping, et al. Dynamic Management System of Ore Blending in an Open Pit Mine Based on GIS/GPS/GPRS[J]. Mining Science and Technology, 2010, 20(1): 132-137. |
| [5] | MA Pan, MENG Lingkui, WEN Hongyan. Kalman Filtering Model of Dynamic Deformation Based on Wavelet Analysis [J]. Geomatics and Information Science of Wuhan University, 2004, 29(4): 349-353.(马攀,孟令奎,文鸿雁. 基于小波分析的Kalman滤波动态变形模型研究[J]. 武汉大学学报:信息科学版,2004,29(4):349-353.) |
| [6] | HUANG Dingfa, CHEN Yongqi, DING Xiaoli, et al. Wavelet Based Analysis Technique for the Monitoring of Tall Stracture under Normal Loading Using GPS[J]. Journal of Vipation and Shock, 2001, 20(1):12-17.(黄丁发,陈永奇,丁晓利,等. GPS高层建筑物常荷载振动测试的小波分析[J]. 振动与冲击,2001,20(1):12-15.) |
| [7] | DAUBECHIES I. Ten Lectures on Wavelets[M]. SIAM: Society for Industrial and Applied Mathematics, 1992: 312-313. |
| [8] | YI TingHua, LI Hongnan, GU Ming. Experimental Assessment of High-rate GPS Receivers for Deformation Monitoring of pidge[J]. Measurement, 2012, 46: 420-432. |
| [9] | WU Jizhong, HUA Xianghong, GAO Junqiang. Feature Extraction of Structure Natural Vipation and Multipath Separation Based on Wavelet Packet Decomposition[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 486-490.(吴继忠,花向红,高俊强. 基于小波包分解的结构自振特征提取及多路径误差分离[J]. 武汉大学学报:信息科学版,2010,35(4):486-490.) |
| [10] | LI Qingwu, HE Chunyuan. A New Thresholding Method in Wavelet Packet Analysis for Image De-noising[C]// Proceedings of IEEE International Conference on Mechatronics and Automation. Piscatawan: IEEE, 2006: 2074-2078. |
| [11] | GUO Xiaoxia, YANG Huizhong. Wavelet Packet De-noising Based on Several Thresholds[C]// Proceedings of the 27th Chinese Control Conference. Beijing: Beihang University Press, 2008: 169-172.(郭晓霞,杨慧中. 基于多阈值的小波包去噪[C]//第27届中国控制会议. 北京: 北京航空航天大学出版社,2008:169-172.//第27届中国控制会议. 北京: 北京航空航天大学出版社,2008:169-172.) |
| [12] | TAN Wencai, ZHANG Qiuju. An Improved De-noising Method by Wavelet Packet Multi-threshold[J]. Journal of Jiangnan University:Natural Science Edition, 2012, 11(2): 178-181.(谭文才,张秋菊. 小波包多阈值去噪的一种方法改进[J]. 江南大学学报:自然科学版,2012,11(2):178-181.) |
| [13] | WU Zhaocai, LIU Tianyou. Wavelet Transform Methods in Seismic Data Noise Attenuation[J]. Progress in Geophysics, 2008, 23(2): 493-499.(吴招才,刘天佑. 地震数据去噪中的小波方法[J]. 地球物理学进展,2008,23(2):493-499. 地球物理学进展,2008,23(2):493-499.) |
| [14] | OGAJA C, RIZOS C, WANG Jingling, et al. A Dynamic GPS System for On-line Structural Monitoring[C] //International Symposium on Kinematic Systems in Geodesy, Geomatics & Navigation (KIS 2001). Banff:[s.n.], 2001: 5-8. |
| [15] | JI Yuebo. Frequency Order of Wavelet Packet[J]. Journal of Vipation and Shock, 2005, 24(3):97-99.(纪跃波. 小波包的频率顺序[J]. 振动与冲击,2005,24(3):96-98.振动与冲击,2005,24(3):96-98.) |
| [16] | GE Zhexue, SHA wei. Wavelet Analysis Theory and MATLAB R2007 Implementation[M]. Beijing: Publishing House of Electronics Industry, 2007: 340-342.(葛哲学,沙威. 小波分析理论与MATLAB R2007实现[M]. 北京:电子工业出版社,2007: 340-342.) |
| [17] | QU Guoqing, DANG Yamin, ZHANG Chuanyin, et al. Analysis and Improvement of De-noising Method for Wavelet Packet[J].Journal of Geodesy and Geodynamics, 2008, 28(4): 102-110.(曲国庆,党亚民,章传银,等. 小波包消噪方法分析及改进[J].. 大地测量与地球动力学,2008,28(4):102-110.) |
| [18] | ZHANG Defeng. Matlab Wavelet Analysis[M]. Beijing: China Machine Press, 2009: 93-97.(张德丰. Matlab小波分析[M]. 北京:机械工业出版社,2009: 93-97.) |
| [19] | VIRMANI J, KUMAR V, KALRA N, et al. SVM-Based Characterization of Liver Ultrasound Images Using Wavelet Packet Texture Descriptors[J]. Journal of Digital Imaging, 2013: 1-14. |
| [20] | TAO Ke, ZHU Jianjun. A Hypid Indicator for Determining the Best Decomposition Scale of Wavelet Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 749-755.(陶珂,朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报,2012,41(5):749-755.) |
| [21] | WU Fumei, YANG Yuanxi. GPS/INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold De-noising[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 124-128.(吴富梅,杨元喜. 基于小波阈值消噪自适应滤波的GPS/INS组合导航[J]. 测绘学报,2007,36(2):124-128.) |