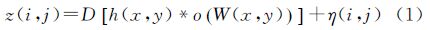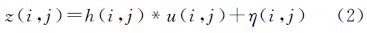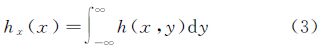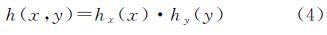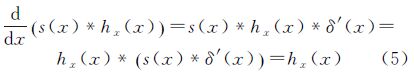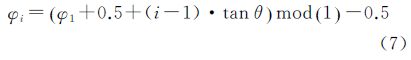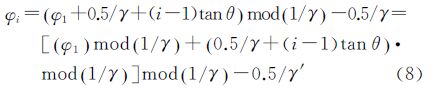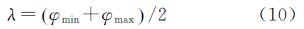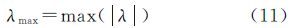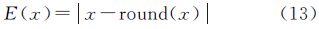2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences,Beijing 10049,China
1 引 言
空间光学遥感相机在地形测绘、环境监测、资源探测等方面有着重要应用,然而由于大气扰动、空间相机与拍摄场景的相对复合运动、相机离焦等诸多因素影响,拍摄的遥感图像会存在一定程度的模糊(blur)[1, 2]。如何从退化模糊的图像中准确提取出点扩散函数(point spread function,PSF),是分析成像指标[3, 4]以及进一步提升图像质量所需要解决的问题。如文献[5]分析了SPOT影像的点扩散函数,对SPOT影像进行了反卷积复原后处理,从而重建获得图像质量更好、空间分辨率更高的影像。而文献[6]将点扩散函数估算运用到遥感影像融合中,从地面边缘纹理中获取点扩散函数信息,用于设计滤波参数,得到了更佳的图像融合结果。
相机在轨点扩散函数的测量是空间光学遥感领域的关键技术。目前,基于捕获的遥感图像测量在轨点扩散函数的方法,根据是否需要特定形状的源目标,可分为两类。其中使用特定源目标的方法目前较常用,如点光源法[7]、矩形脉冲法(pulse method)[8]、阶跃响应法(step-edge method)[9, 10, 11]等。点光源法原理简单,但地面点光源靶标较难实现;矩形脉冲法需要狭缝状目标的准确宽度信息;最为常用的还是阶跃响应法,其源目标可以是铺设的靶标,也可以是遥感图像中检测到的屋顶、海岸等[12, 13],而且它对校直(alignment)问题不十分敏感,稳健性好[14]。对源目标形状无特定要求的方法[15, 16],虽能节约靶标铺设成本,但由于该类方法在稳定性和精度上还有待提升,故目前并不常用[17]。
本文以空间光学遥感相机为重点研究对象,分析了遥感图像退化模型。为了精确测量在轨点扩散函数,理论分析了阶跃图像性质对PSF计算精度的影响,并提出了阶跃图像选择标准,以及采样相位弱化方法。通过对实际遥感图像的试验,验证了所提方法的稳定性和有效性。
2 遥感图像退化过程有着连续亮度函数o(x,y)的地面场景,通过空间相机的光学系统会发生扭曲形变(warping),原场景的退化过程可建模为卷积点扩散函数h(x,y)。最终CCD器件对其离散量化,生成数字图像z(i,j),整个成像过程可用式(1)表示
式中,η为加性噪声;W表示几何形变;D[·]为抽样算子;*表示卷积。不考虑几何形变时,更常用的数字图像退化模型如式(2)所示
式中,h(i,j)、u(i,j)分别表示离散化的PSF和原场景的数字图像。该退化模型成立的前提是,点扩散函数h对于整幅图像u是线性、空间移不变的。对于连续信号输入、离散信号输出的采样成像系统,离散系统点扩散函数h(i,j)与空间位置存在虚假相位相关性[18],虽然在微观上PSF与位置相关,但是在宏观上可认为采样成像系统具有全局移不变性[19]。因此,从图像中测得的在轨点扩散函数为系统平均点扩散函数(average system point spread function,ASPSF),为宏观参量。
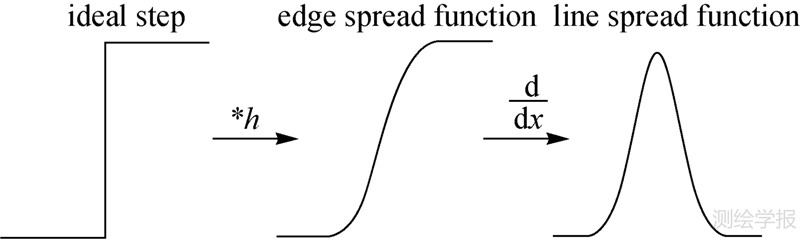
3 在轨点扩散函数测量方法 3.1 阶跃响应法思想设垂轨(across-track)方向为x轴方向,沿轨方向(along-track)为y轴方向,以垂轨方向阶跃为例,阶跃响应法的原理如图 1所示。所得线扩散函数(line spread function,LSF)hx(x)与二维PSF关系如式(3)所示
|
| 图 1 阶跃响应法示意图 Fig. 1 Brief explanation of step-edge method |
同理,由沿轨方向阶跃可以得到对应的线扩散函数hy(y),对于可以空间分离变量的h(x,y),有
而对一般遥感系统,这种可分离性是有效的。
图 1中,一维理想阶跃信号s(x)退化得到边缘扩散函数(edge spread function,ESF),对ESF求一阶导数则有
式中,δ′(x)表示Delta函数的一阶导数。式(5)表明,对地面场景中的理想阶跃目标,从退化后的图像中提取其边缘扩散函数后求导即可得到LSF。由垂轨和沿轨方向的两个LSF结合式(4)即可给出二维PSF。
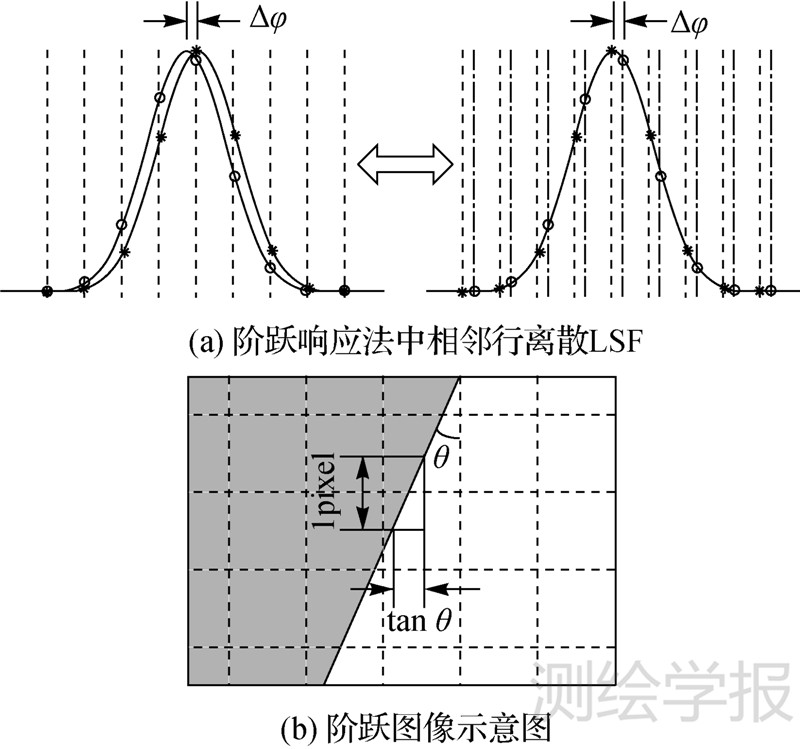
3.2 提高测量精度的方法实际遥感相机为采样成像系统,为了消除虚假相位的影响,阶跃响应法对多行有微小采样相位(sampling phase)差异的边缘扩散函数移位取均值。该操作等效于对点扩散函数进行多次采样,每次对应不同的采样网格(sampling grid),如图 2所示。图 2(a)中所示的相邻行之间的采样相位差与阶跃边缘倾斜角度有关,以垂轨方向阶跃为例,其关系如图 2(b)所示。设阶跃边缘线与竖直方向夹角为θ,则相邻行采样相位差为
|
| 图 2 阶跃图像与相邻行离散LSF Fig. 2 Sketch map of the step-edge image and the adjacent lines |
设参与计算的阶跃图像行数为l,即对点扩散函数进行了l次不同位置的采样,其中第1行的采样相位为φ1(-0.5≤φ1 <0.5,单位为像素),以其为参考第i (0≤i≤l)行的采样相位为
式中,(A)mod(B)表示A对B取模数(modulus)。为了抑制采样相位对测量结果的影响,集合{φi|0≤i≤l}中元素需要尽量对称分布在0值两边。在实际的遥感图像中,由于地面像元分辨率以及阶跃目标实际尺寸的限制,阶跃图像行数的值l通常不会太大,由式(7)得到的φi在[-0.5 0.5]区间分布随机性很大,需要通过对ESF插值来缩小采样相位区间。若对原始ESF每两个点之间插(γ-1)个点,插值后的ESF相邻数据之间距离为(1/γ)像素,对应φi为
此时φi需要在[-0.5/γ 0.5/γ]范围内对称分布。
虽然插值可以减小(φ1)mod(1/γ)的值,从而弱化φ1的影响,但是γ不是取值越大越好,γ取值需要避免
的情况。若式(9)成立,每行ESF偏移的相位很小,那么式(8)的结果由 (φ1)mod(1/γ)主导,如θ=0时,式(8)的值完全取决于(φ1)mod(1/γ)。对于选定的阶跃图像,θ值已固定,而γ是处理中可控的,在插值中需避开使得tanθ与1/γ成整数倍关系的γ取值。
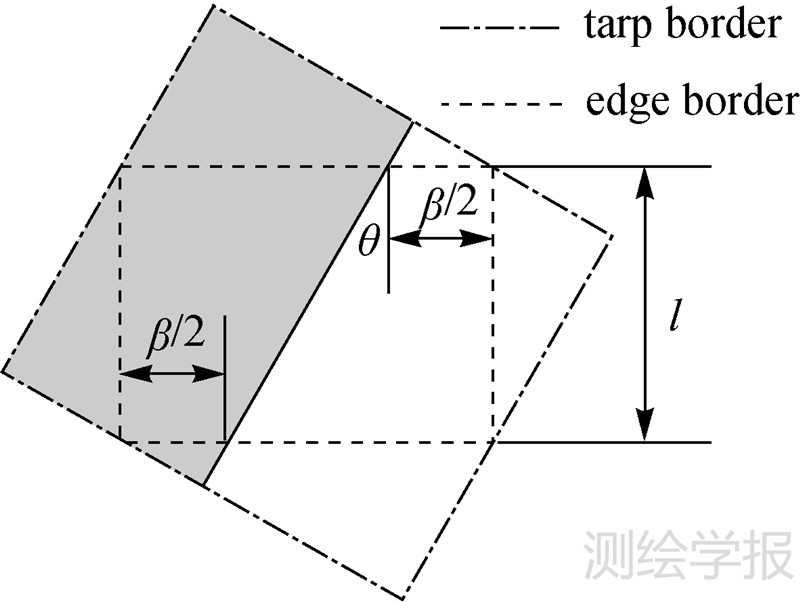
理论上,阶跃响应法对角度θ并无要求,但是对靶标铺设和阶跃图像选取有一定的影响。阶跃响应法所铺设的靶标通常为矩形油布,对于图 3所示倾角为θ的靶标,用于计算的有效尺寸为l×β,而需要的油布尺寸为(βsinθ+l/cosθ)×(βcosθ+2lsinθ)。倾角越大,同样的有效尺寸所需要的油布尺寸越大,故而铺设靶标时θ不应过大。
|
| 图 3 铺设的靶标与可用于计算的图像尺寸关系图 Fig. 3 Brief explanation of the relationship between physical tarp and step-edge image |
设集合{φi|0≤i≤l }中最小元素为φmin,最大元素为φmax,则可以通过比较
偏离0值的幅度来判断对称性。
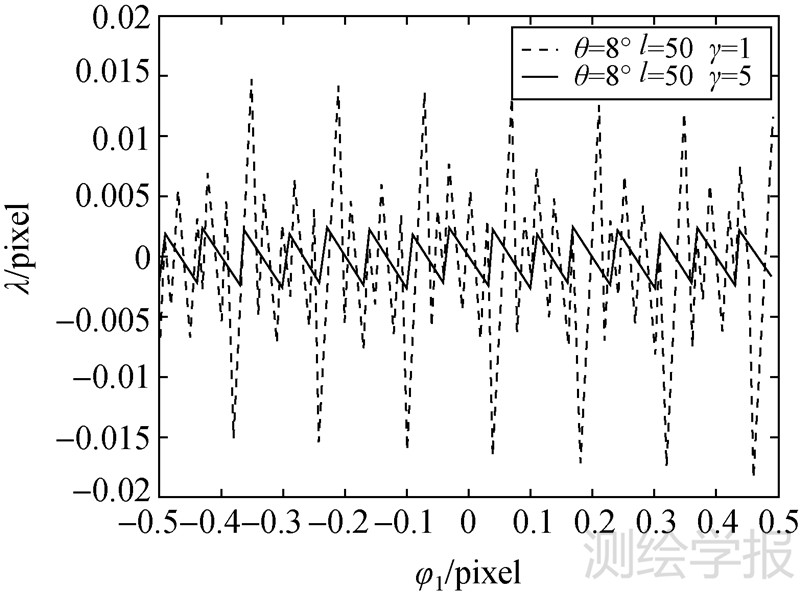
图 4所示为θ=8°、l=50,γ分别为1和5时,λ随φ1的变化曲线。当γ=1时,虽然λ也能在某些φ1处接近0,但是整体曲线随φ1变化幅度大,即测量不确定度大。如果考虑在不同φ1下最坏的情况,即
|
| 图 4 θ、l相同,γ不同时λ随φ1变化曲线 Fig. 4 λ-φ1 curves for fixed θ and l |
图 4中γ=1时,λmax=0.018 4;γ=5时,λmax=0.002 7。θ、l固定,λmax随γ增大时的变化曲线如图 5所示。在实际应用中,当阶跃目标图像选定,θ、l即固定,需要通过图 5所示的曲线来判定合适的γ。

|
| 图 5 θ、l固定,λmax随γ变化曲线 Fig. 5 λmax-γ curve for fixed θ and l |
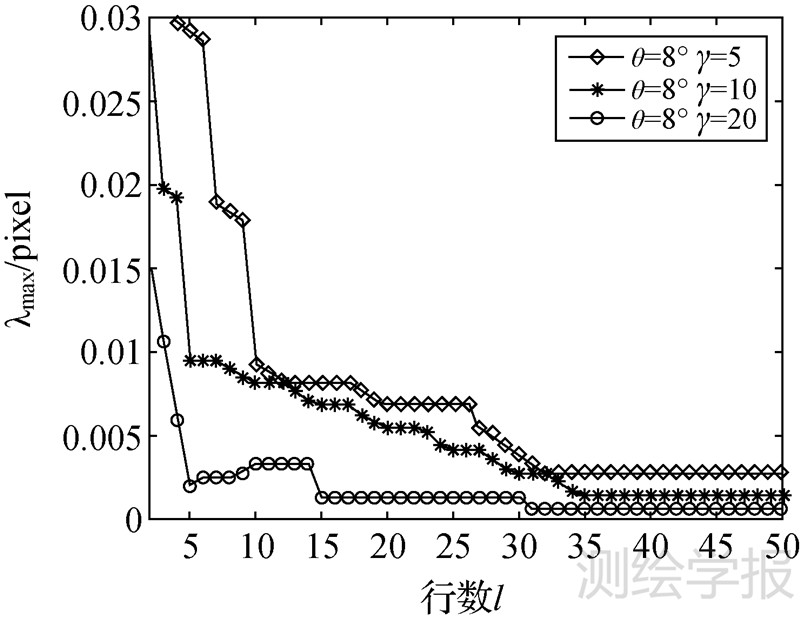
图 6所示为θ=8°,γ分别为5、10、20时,λmax随l的变化情况。总的来说,尽可能大的l可以使λmax越小,进而使PSF测量结果更精确。
|
| 图 6 θ固定,λmax随l变化曲线 Fig. 6 λmax-l curves for fixed θ |
实际捕获的遥感图像是经过量化的,在同样的量化间隔下,图 1所示理想阶跃幅度越大,量化得到的ESF中细节层次越多。形象地说,对图 2所示阶跃图像,其低亮度区域与高亮度区域的亮度比为10∶20和100∶200时测量结果的准确度是不一样的。定义R来表征阶跃图像对比度
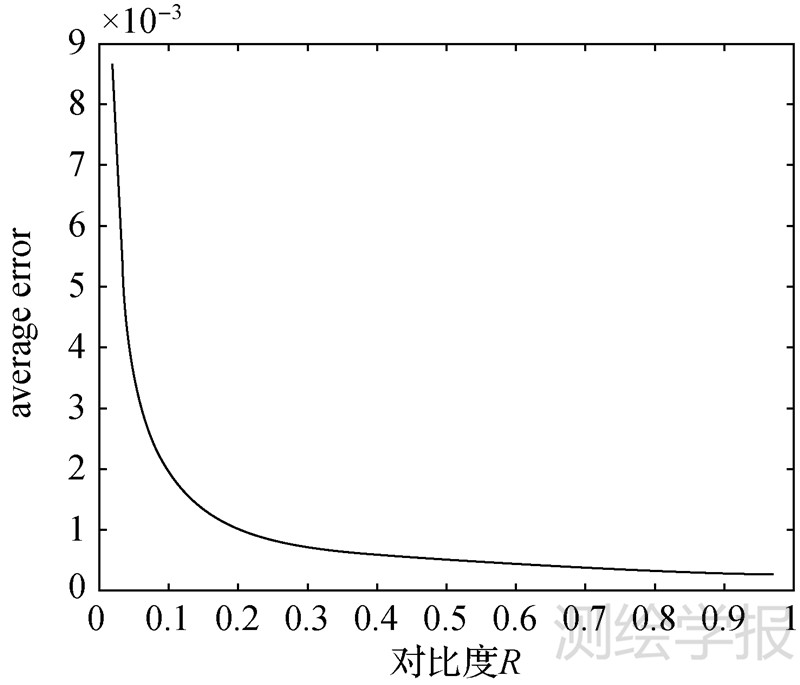
式中,Imax、Imin分别为阶跃图像较暗区域及较亮区域分别的灰度值;ID为动态范围(对于10 B遥感数据,动态范围为1023)。阶跃图像中阶跃越大,则R值越大。图 7所示为量化值与真实值之间的误差均值与R的关系,其中误差E定义为
round表示四舍五入运算。
|
| 图 7 误差均值与R的关系曲线 Fig. 7 Curve of relationship between average error and R |
由以上分析可知,使用R值较大的阶跃图像计算ASPSF时受量化误差影响小。要达到较大的R值,有两个途径:场景中目标本身亮度差异大和调节CCD增益。
场景中本身的亮度差异除了与地面场景反射率及太阳高角有关,此外,太阳高角还影响遥感影响中的随机噪声,太阳高角小时,图像信噪比(signal to noise ratio,SNR)小。为了减小随机噪声的影响,通常选取中午12时至下午2时之间拍摄的遥感图像计算PSF。
虽然增大CCD增益可以获得较大的R值,但是也易造成原先亮度很大的区域像素饱和。像素饱和会导致信息丢失,如图 8所示,在应用中应避免使用严重像素饱和的阶跃图像计算点扩散函数。

|
| 图 8 像素饱和的ESF与实际ESF Fig. 8 Difference between the saturated and real ESF |
为了提高遥感相机的在轨点扩散函数测量精度,需要考虑如下几点:
(1) 若铺设靶标,则阶跃倾斜角度θ不宜过大。
(2) 选择阶跃图像时,要求ESF行数l尽量大;在像素不存在饱和的情况下,对比度R需尽量大;为了减小随机噪声的影响,应选取太阳高角接近90°时候捕获的图像。
(3) 阶跃图像选定后,对固定的l、θ,要选取能使λmax较小的γ值来削弱采样相位的影响。
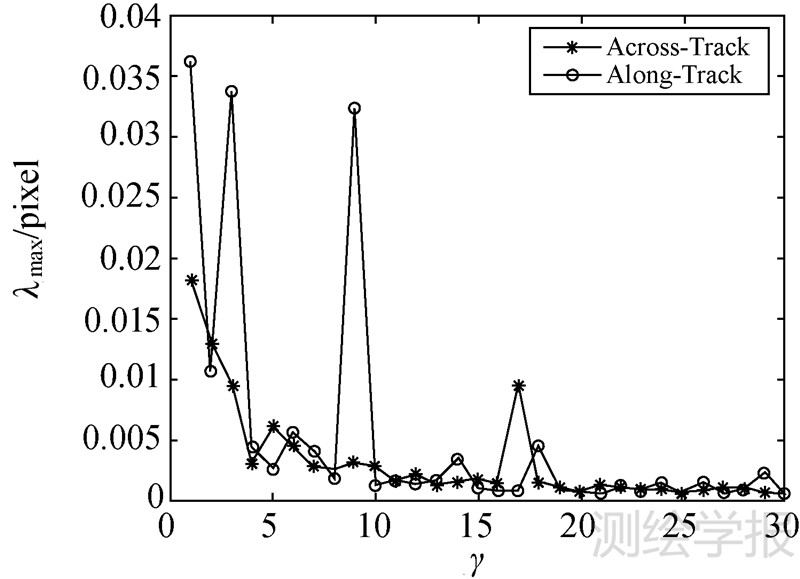
4 试验及讨论 4.1 点扩散函数测量试验中使用遥感相机全色谱段图像,地面像元分辨率5 m,量化位数10位,拍摄于当地时间下午2时左右。由包含阶跃的地面场景(图 9(a)、(b))中,选择了对比度大的地面靶标作为计算点扩散函数的阶跃图像,如图 9(c)所示。垂轨与沿轨方向阶跃图像的参数如表 1所示。根据第3节的分析,计算得到图 10所示的两个方向上λmax随γ的变化关系,选取该范围内令λmax最小的γ值,垂轨方向为25,沿轨方向为27。对阶跃图像分别计算得到的插值后LSF如图 11(a)所示,由两个方向的LSF合成得到的二维PSF如图 11(b)所示。

|
| 图 9 阶跃图像选取 Fig. 9 Candidate edges and selected step-edge images |
| step-edge image | across-track | along-track |
| θ/(°) | 5.6 | 6.4 |
| l | 45 | 44 |
| R/(%) | 86.7 | 87.8 |
|
| 图 10 沿轨方向与垂轨方向γ值选取 Fig. 10 Brief explanation of selecting proper γ in both directions |

|
| 图 11 垂轨方向于沿轨方向的插值LSF以及插值PSF Fig. 11 Interpolated LSFs of across-track and along-track directions and the interpolated PSF |
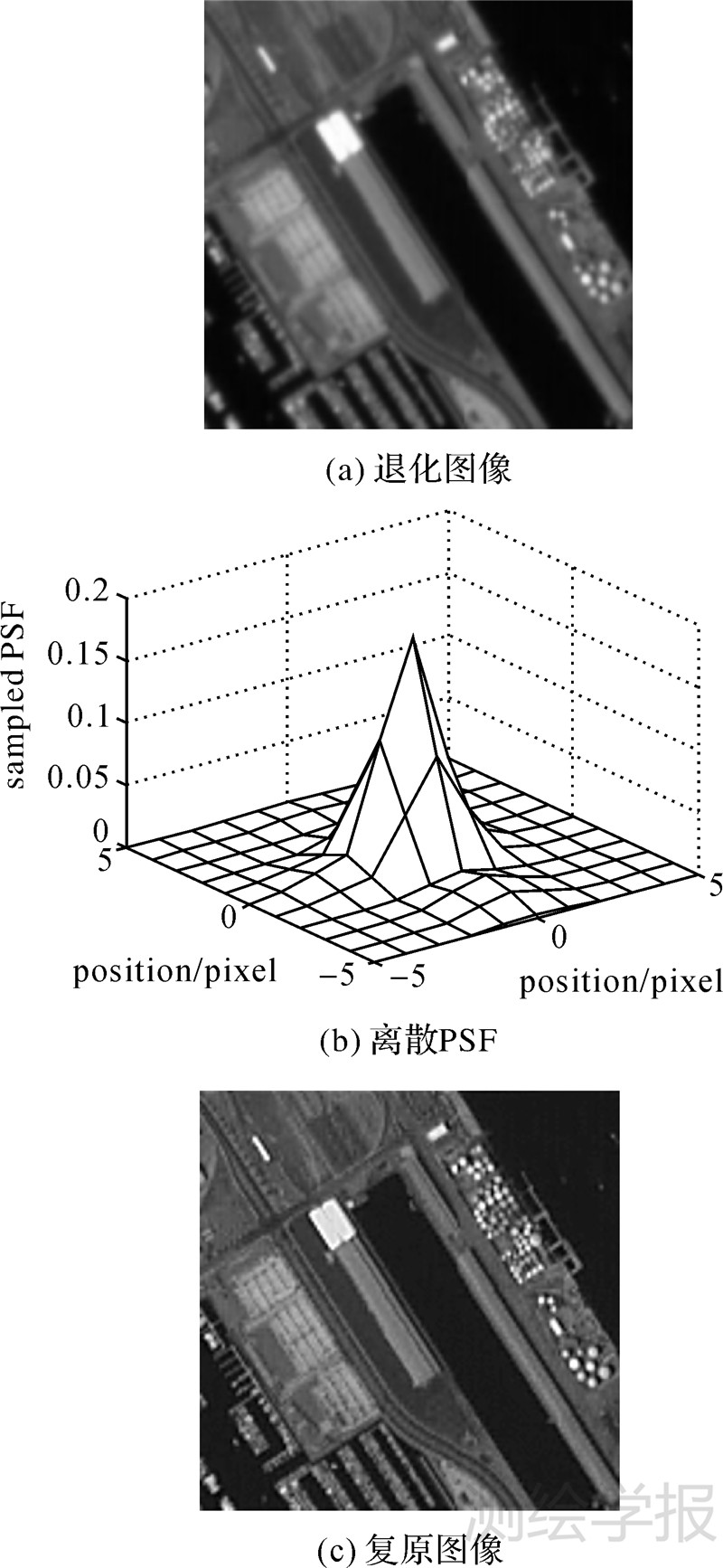
基于式(2)的退化模型进行图像复原时,需要对图 12(b)所示PSF重采样,使其分辨率与退化图像相同。试验中使用有约束的最小乘方滤波法进行图像复原,结果如图 12(c)所示。
|
| 图 12 基于所测PSF的图像复原 Fig. 12 Image restoration based on measured PSF |
分别用细节信号能量(energy of details,EOD)[10]、灰度平均梯度(gray average gradient,GMG)、拉普拉斯能量和(energy of Laplacian,EOL)[20]作为图像复原效果的客观评价指标,复原前后图像质量对比如表 2所列。由表 2可知,复原后图像的细节信号能量提升92%,灰度平均梯度上提升104%,拉普拉斯能量和提升173%。图像复原结果也验证了PSF测量的准确性。
| degraded | restored | improved/(%) | |
| EOD | 3462.8 | 6643.3 | 92 |
| GMG | 7.1 | 14.5 | 104 |
| EOL | 11.3 | 30.8 | 173 |
本文深入分析了阶跃图像性质对测量空间相机在轨点扩散函数的影响,提出了一种提高测量精度的方法。通过选择合适的阶跃图像,并弱化采样相位的影响,获得高精度的PSF测量结果。基于所测PSF对退化图像进行了复原,复原后图像细节信号能量提升92%,灰度平均梯度上提升104%,拉普拉斯能量和提升173%。试验结果表明,该测量方法可获得高精度的在轨点扩散函数,为分析遥感系统成像质量和进一步的图像复原提供了重要依据。
| [1] | XU Huanyu, SUN Quansen, XIA Deshen. Restoration of Irregular Sampled Remote Sensing Image Based on NLTV [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2):232-238. (徐焕宇,孙权森,夏德深.基于非局部总变差的消除不规则采样遥感图像复原方法[J].测绘学报,2012, 41(2):232-238.) |
| [2] | SONG Yigang, XIAO Liang, WEI Zhihui, et al. Variable Splitting Iterative Fast Algorithm for Remote Sensing Image Recovery [J]. Acta Armamentarii, 2012, 33(3):283-289.(宋义刚,肖亮,韦志辉,等.光学遥感图像变量分裂迭代快速复原算法[J].兵工学报,2012,33(3):283-289.) |
| [3] | HUANG Chengquan, KALLURI S N V, TOWNSHEND J R G, et al. Assessing and Deconvolving the Impacts of the Point Spread Function on Satellite Remote Sensing [C]//IEEE Geoscience and Remote Sensing Symposium Proceedings.Seattle:[s.n.],1998. |
| [4] | GUO Qiang, YANG Changjun, WEI Caiying. A New Approach to the On-orbit Evaluation of Point Spread Function of Thermal Infrared Images with Applications to FY-2 Satellite Products [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3):1598-1612. |
| [5] | TAN Bing, XU Qing, XING Shuai, et al. Wavelet Super-resolution Algorithm and Its Application to SPOT Images [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3):233-238. (谭兵,徐青,刑帅,等.小波超分辨率重建算法及其在SOPT影响中的应用[J].测绘学报,2004, 33(3):233-238.) |
| [6] | ZHANG Ying, HE Binbin, LI Xiaowen, et al. Remote Sensing Image Fusion of Beijing-1 DMC+ 4 Microsatellite Based on MTF Filter [J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3):223-228. (张瑛,何彬彬,李小文,等.基于MTF 滤波的北京一号小卫星遥感影像融合[J].测绘学报,2009, 38(3):223-228.) |
| [7] | LEGER D, DUFFAUT F, FOBINET F. MTF Measurement Using Spotlight [C]//Proceedings of Geoscience and Remote Sensing Symposium.Pasadena:[s.n.],1994,4:2010-2012. |
| [8] | CHOI T. IKONOS Satellite on Orbit Modulation Transfer Function (MTF) Measurement Using Edge and Pulse Method [M]. Brookings: South Dakota State University, 2002. |
| [9] | NUGENT P W, SHAW J A, KOHOE M R, et al. Measuring the Modulation Transfer Function of an Imaging Spectrometer with Rooflines of Opportunity [J]. Optical Engineering, 2010, 49(10):103201. |
| [10] | ZHAO Huijie, QIN Baolong, JIA guorui. On-orbit Detection for Modulation Transfer Function of Hyperspectral Remote Sensing System [J]. Optics and Precision Engineering, 2011, 19(6):1235-1243. (赵慧洁,秦宝龙,贾国瑞. 高光谱遥感系统调制传递函数的在轨测试 [J]. 光学精密工程, 2011, 19(6):1235-1243.) |
| [11] | XU Baoshu, SHI Zelin, FENG Bin. Modulation Transfer Function Measurement Method of Electro-optical Imaging System [J]. Acta Optica Sinica, 2011, 31(11):1111004. (徐宝树,史泽林,冯斌. 一种光电成像系统调制传递函数的测量方法[J].光学学报, 2011, 31(11):1111004.) |
| [12] | RYAN R, BALDRIDGE B, SCHOWENGERDT R A, et al. IKONOS Spatial Resolution and Image Interpretability Characterization [J]. Remote Sensing of Environment, 2003, 88:37-52. |
| [13] | WANG Ke, XIAO Pengfeng, FENG Xuezhi, et al. The Modified Algorithm of Image Edge Features Detection Based on 2D Discrete Hilbert Transfrom [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. (王珂,肖鹏峰,冯学智,等.基于改进二维离散希尔伯特变换的图像边缘检测方法[J].测绘学报,2012, 41(3): 421-427.) |
| [14] | ZHANG Ying. Imaging MTF of Space Camera under Vibration and Simulation [J]. Optics and Precision Engineering, 2011, 19(9):2146-2153. (张影. 空间相机的颤振成像调制传递函数及仿真实验 [J]. 光学精密工程, 2011, 19(9):2146-2153.) |
| [15] | DELVIT J, LEGER D, ROQUES S, et al. Modulation Transfer Function Estimation from Nonspecific Images [J].Optical Engineering, 2004, 43(6), 1355-1365. |
| [16] | GUO Lingling, WU Zepeng, ZHANG Liguo, et al. Multichannel Blind Deconvolution-Based on-orbit Estimation of Point Spread Function for Space Optical Remote Sensors[J]. Acta Optica Sinica, 2013, 33(4): 245-252. (郭玲玲,吴泽鹏,张立国,等.基于多通道盲反卷积的空间光学遥感器在轨点扩展函数估算[J].光学学报,2013, 33(4): 245-252.) |
| [17] | GUO Lingling, WU Zepeng, ZHANG Liguo, et al. New Approach to Measure the On-orbit Point Spread Function for Spaceborne Imagers [J]. Optical Engineering, 2013, 52(3): 33602-01—33602-06. |
| [18] | PARK S K, SCHOWENGERDT R, KACZYNSKI M A. Modulation-transfer-function Analysis for Sampled Image Systems [J]. Applied Optics, 1984, 23(15), 2572-2582. |
| [19] | HOLSR G C. Imaging System Fundamentals [J]. Optical Engineering, 2011, 50(5): 52601-01—52601-10. |
| [20] | WEN Bo, ZHANG Qiheng, ZHANG Jianlin. Realization of Iterative Blind Image Restoration by Self Deconvolution and Increment Wiener Filter [J]. Optics and Precision Engineering, 2011, 19(12):3049-3055. (温博,张启衡,张建林. 应用自解卷积和增量Wiener滤波实现迭代盲图像复原 [J]. 光学精密工程, 2011, 19(12):3049-3055.) |