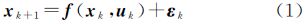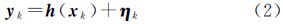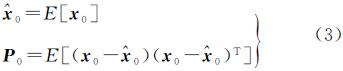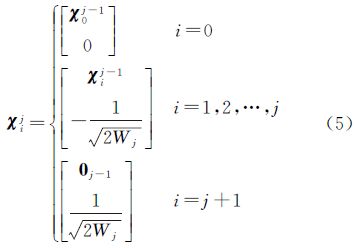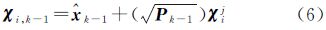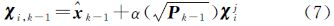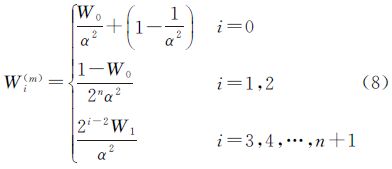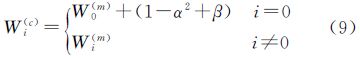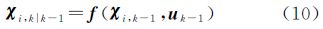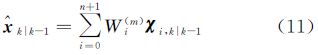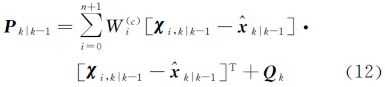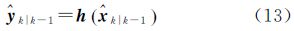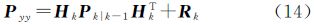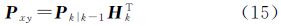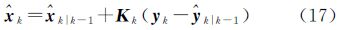2. 中国科学院 国家授时中心，陕西 西安 710600
2. National Time Service Center,Chinese Academy of Sciences,Xi’an 710600,China
1 引 言
控制卫星定轨中非线性模型线性化误差影响一直是卫星定轨领域的研究热点之一。扩展Kalman滤波(extended Kalman filter，EKF)是其中较为常用的一种方法[1, 2]。非线性卫星动力学模型的线性化带来的误差也可以通过观测信息进行补偿，即采用自适应Kalman滤波方法[3, 4, 5]。通过观测信息与动力学模型信息比较得到的差值来控制动力学模型的影响，于是产生了自适应滤波定轨技术[6]。
近年来，无味Kalman滤波(unscented Kalman filter，UKF)[7]作为一种非线性滤波新方法，引起了广泛关注。UKF在卫星定轨问题中已逐渐得到了应用，并显示了其在处理强非线性系统方面的优越性[8, 9]。UKF算法的估计精度和计算效率随采样策略的不同而有所差别，这是因为采样策略不同，所需的采样点数也会不一样。一般采样点数越多，估计精度越高，但相应的计算效率也越低。因此，如何在估计精度和计算效率之间找到一种平衡，或者在保证估计精度不明显降低的情况下，尽量提高算法的计算效率，这是应用UKF的关键技术之一[10, 11]。
在星载GPS卫星定轨中，通常以卫星的三维位置和速度为轨道参数，卫星运动的状态方程显然是强非线性的；卫星运动的观测方程是GPS距离观测方程，其线性化误差很小，与前者相比，观测方程无疑是弱非线性的。
在综合考虑估计精度和计算效率的情况下，本文提出一种将UKF和EKF相结合的星载GPS卫星定轨新算法。该算法充分考虑了星载GPS卫星定轨模型结构特点，一方面利用UKF来处理系统的强非线性部分，以保证较高的估计精度，同时改进了其采样策略，通过减少采样点数、减少采样次数来提高其计算效率；另一方面利用EKF来处理系统的弱非线性部分，即在保证估计精度不明显降低的同时，尽量进一步提高系统的计算效率。
2 星载GPS卫星定轨算法假设卫星运动系统的状态方程和观测方程分别为如下离散的非线性方程
式中，xk、uk、εk和Qk分别为系统状态向量、输入控制向量、系统动态噪声向量及其协方差阵(见式(12))；yk、ηk和Rk分别为观测向量、观测噪声向量及其协方差阵(见式(14))。系统状态向量xk的维数为n，观测向量yk的维数为m，εk与ηk线性无关。
EKF是至今为止应用最为广泛的一种非线性滤波算法，也是卫星定轨领域的一种经典算法。对于卫星定轨而言，有关文献已经验证了UKF算法的估计精度优于EKF算法，但计算效率低于EKF算法[8, 12, 13, 14, 15, 16]。
如何设计一种融合算法，既能利用经典EKF算法的高效性，又能倚重UKF算法的高精度，这是本文研究的出发点。
2.1 改进的UKF算法采样策略是UKF算法的核心，所以要改进UKF算法，提高UKF算法的计算效率，并保持较高的估计精度，必须先从算法的采样策略进行考虑。
UKF算法的计算效率与采样点数成正比。常用的对称采样策略，在状态向量不扩维的情况下，采样点个数为2n+1，其中n为状态向量的维数。对于UKF算法而言，采样点数最少的方案是单形采样策略。所谓单形采样策略，是指采样点能够构成一个单形，如二维空间的单形是三角形，三维空间的单形是四面体，等等。因此，对于n维空间情形，至少需要n+1个采样点才能构成一个单形[17]。由于随机变量x的均值所包含的分布信息最多，所以常把x的均值也作为一个采样点，称为中心点，故包含中心点的单形采样点个数为n+2。如果罚函数要求偏度最小，就可以得到最小偏度单形采样策略，该采样策略能在匹配前两阶矩的前提下使得3阶矩(即偏度)最小，确保了对于任意分布达到2阶截断精度，对于高斯分布可达到3阶截断精度[18]。因此，采用最小偏度单形采样策略，最有利于提高UKF算法的计算效率，并能保持比较高的估计精度。
值得注意的是，最小偏度单形采样策略中采样点非中心对称，并随着维数的增加，采样点至中心点的距离也会随之增大，产生采样的非局部效应，而且还会导致高阶项的误差增大[17]。为降低这类影响，文献[17]提出了一种比例UT变换(unscented transformation)方法，即对UT变换中的采样策略进行比例修正，通过调整参数α的值来解决非局部效应和高阶项误差等问题，并通过参数α和β来保证预测协方差矩阵的半正定性[17]。
将比例修正引入到最小偏度单形采样策略的UKF算法中，便得到了改进的UKF算法。限于篇幅，这里不再给出改进的UKF算法的具体公式，可参考文献[10, 11, 17, 18]。
2.2 UKF-EKF算法星载GPS卫星运动的动力学模型，复杂且强非线性。若单纯采用EKF算法，精度有时难以保证，甚至导致滤波发散；若单纯采用UKF算法，计算效率有时不能满足任务要求。为了在保证精度要求的前提下，进一步提高算法的计算效率，笔者在上述改进的UKF算法的基础上，将UKF算法和EKF算法相融合，建立了UKF-EKF算法。
UKF-EKF算法，其基本思想是，对星载GPS卫星运动的状态方程部分，即动力学模型部分，由于现在星载GPS卫星定轨大多选择三维位置和速度为轨道参数，所以这部分是强非线性的，采用改进的UKF算法；对星载GPS卫星运动的观测方程部分，由于GPS距离观测方程的线性化误差很小，这部分相对来说是弱非线性的，采用高效的EKF算法，两者融合统一，可以达到比较好的滤波效果。
根据上述基本思想，新设计构造的UKF-EKF算法如下：
(1) 状态初始化
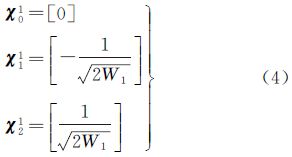
(2) 计算采样点集及相应权值
采样点初始化向量(j=1(对应状态为1维))
采样点扩展向量(j=2,3，…,n时(对应状态为j维))
加入均值和协方差信息
比例修正
确定采样点权值(取0≤W0≤1)
(3) 时间更新
(4) 观测更新
以上各式中，χij为j维空间采样点集中的第i个采样点；权值Wi(m)、Wi(c)，上标m和c分别表示计算均值和协方差阵时所取的权值；α和β为参数，比例因子α用以控制采样点至中心点的距离，是一个较小的正数，取值区间为[10-4,1]，β用来引入随机变量x分布的先验信息，若服从高斯分布，则取β=2为最优；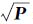
表示P的平方根矩阵，可用下三角的Cholesky分解法来计算，若P=UUT，则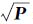=U，显然P应为半正定矩阵； Hk=
。
UKF-EKF算法与上述改进的UKF算法相比，前两部分(即状态初始化和采样点集及相应权值的计算)完全相同；第3部分时间更新，UKF算法进行了第2次重新采样，以计算观测值预报值，而UKF-EKF算法没有第2次重新采样，直接通过观测方程来计算观测值预报值，这样设计也是为了提高UKF-EKF算法的计算效率；第4部分观测更新，形式上看，UKF-EKF算法与UKF算法非常类似，只是Pyy和Pxy计算式不同，但实质上，UKF-EKF算法的观测更新部分采用的是EKF算法的相应算式。
3 算例分析为了对比分析上述几种星载GPS卫星定轨算法的性能，本文选用CHAMP卫星于2003年064年积日10:00-11:30时段内(约一个轨道周期)所采集的GPS观测数据进行轨道解算处理。GPS观测数据，采用的是双频相位消电离层线性组合的非差观测值。
对应于EKF算法、改进的UKF算法和本文提出的UKF-EKF算法，采用了3种解算方案逐点估计卫星轨道状态，分别是：EKF方案、UKF方案、UKF-EKF方案。其中在UKF方案、UKF-EKF方案中，根据演算情况，比例因子α和参数β取值分别为α=0.000 5、β=2。为了单纯地比较各种方案的估计精度和计算效率，对GPS观测数据进行了统一的数据预处理，所以没在各种方案中再嵌入抗差处理、自适应处理等功能模块，这样的比较排除了附加的影响，应更具有说服力。
这里以德国GFZ提供的CHAMP卫星事后处理精密科学轨道作为参考轨道。3种方案的定轨结果分别与参考轨道的相应量进行互差对比，情况如图 1-图 6所示，相应的RMS(误差的均方根)[19]如表 1所示。
|
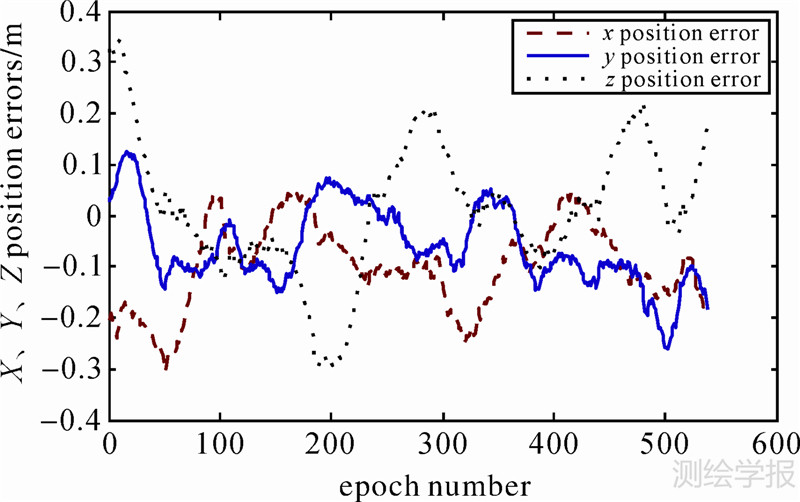
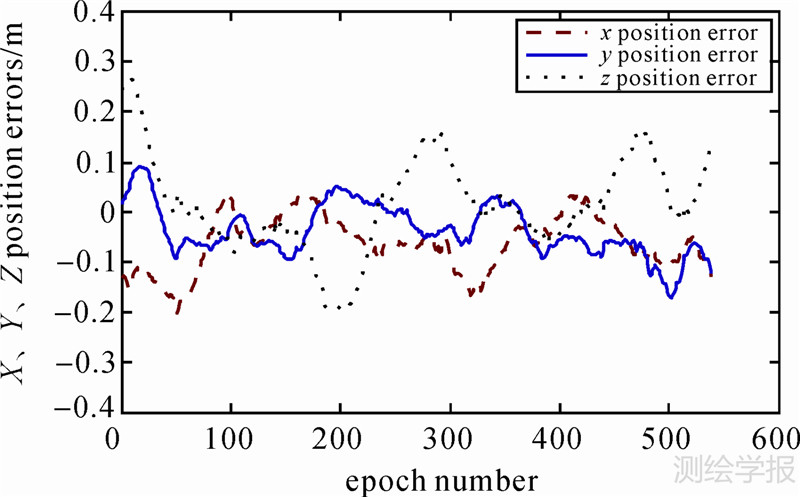
| 图 1 EKF方案的位置误差 Fig. 1 Position errors of EKF strategy |
|
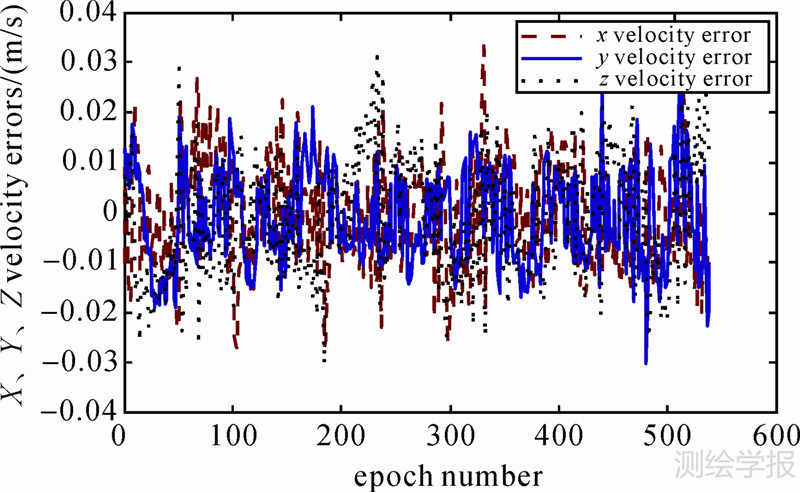
| 图 2 EKF方案的速度误差 Fig. 2 Velocity errors of EKF strategy |
|
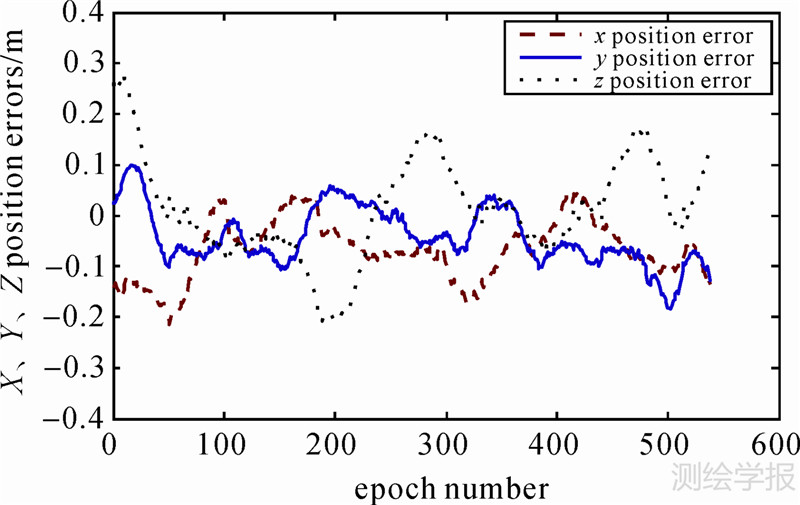
| 图 3 UKF方案的位置误差 Fig. 3 Position errors of UKF strategy |
|
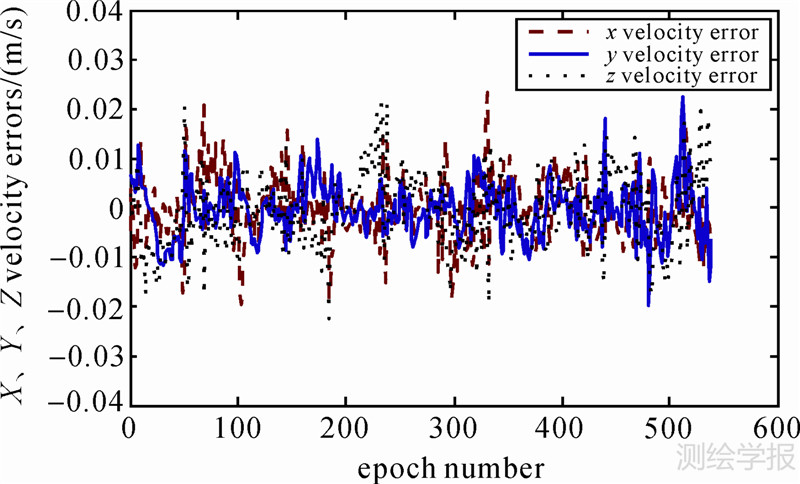
| 图 4 UKF方案的速度误差 Fig. 4 Velocity errors of UKF strategy |
|
| 图 5 UKF-EKF方案的位置误差 Fig. 5 Position errors of UKF-EKF strategy |
|
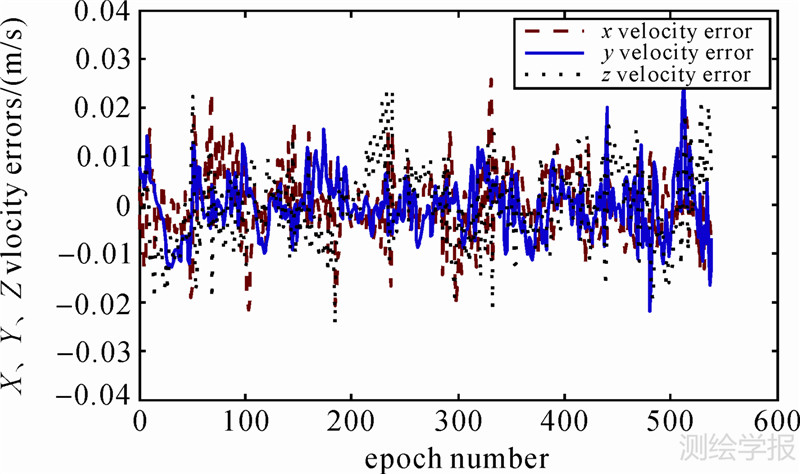
| 图 6 UKF-EKF方案的速度误差 Fig. 6 Velocity errors of UKF-EKF strategy |
| 方 案 | 位置RMS/m | 速度RMS/(m/s) | |||||
| X方向 | Y方向 | Z方向 | X方向 | Y方向 | Z方向 | ||
| EKF | 0.128 5 | 0.098 3 | 0.132 3 | 0.010 6 | 0.009 7 | 0.012 2 | |
| UKF | 0.083 4 | 0.063 5 | 0.094 0 | 0.006 2 | 0.005 4 | 0.007 4 | |
| UKF-EKF | 0.089 2 | 0.069 9 | 0.100 8 | 0.006 9 | 0.006 0 | 0.008 2 | |
图 1、图 2为EKF方案定轨结果与参考轨道的对比情况。可以看出，EKF方案定轨结果的误差偏大，这是由于EKF方案在递推滤波的过程中，将系统强非线性的状态方程和略非线性的观测方程均进行了线性化处理，线性化误差的影响较大，从而导致定轨结果的误差相对偏大。
图 3、图 4为UKF方案定轨结果与参考轨道的对比情况。与图 1、图 2相比，图 3、图 4的误差幅度明显变小，表明UKF方案比EKF方案定轨结果的误差要明显小一些，这是因为UKF方案在递推滤波的过程中，没有将系统非线性的状态方程和观测方程进行线性化处理，而是采用分布逼近的思想，来递推求解下一历元的均值和协方差阵，从而不受线性化误差的影响，所以结果的误差也较小。
图 5、图 6为UKF-EKF方案定轨结果与参考轨道的对比情况。与图 1、图 2相比，图 5、图 6的误差幅度也明显较小；与图 3、图 4相比，图 5、图 6的误差幅度非常接近前者，对比表明UKF-EKF方案比EKF方案定轨结果的误差要明显小一些，与UKF方案定轨结果的误差比较接近，这是因为UKF-EKF方案在递推滤波的过程中，系统强非线性的状态方程没作线性化处理，以确保滤波的精度；同时系统弱非线性的观测方程进行线性化处理，滤波的精度稍有降低，从图示情况看，UKF-EKF方案定轨结果的精度明显优于EKF方案，稍弱于但很接近于UKF方案。
表 1给出了3种方案定轨结果的RMS统计结果。可以看出，UKF-EKF方案定轨结果的位置RMS(0.089 2 m、0.069 9 m、0.100 8 m)分别明显小于EKF方案的位置RMS(0.128 5 m、0.098 3 m、0.132 3 m)，但与UKF方案的位置RMS(0.083 4 m、0.063 5 m、0.094 0 m)相差不大，可以说基本相当；3种方案的速度RMS对比情况与位置RMS对比情况类似。所以，表 1给出的统计结果与图 1-图 6对比分析的结果是一致的。
值得说明的是，虽然UKF方案、UKF-EKF方案的位置RMS、速度RMS分别相差不大，基本相当，但UKF-EKF方案的相应量还是稍大一点，这是符合算法设计预期的，因为UKF-EKF算法减少了一次采样，观测更新部分也进行了简化，这正是造成两种方案差异的主要原因，统计结果也正好反映了差异的大小。
计算效率是3种方案对比的另一个重要方面。在本算例中，对3种方案的计算效率进行了相应的统计，基本情况是，EKF方案明显高于UKF方案和UKF-EKF方案，UKF-EKF方案也要高于UKF方案。根据计算条件或硬件的不同，3种方案计算的具体耗时量会有所不同，但耗时量间的数量关系大体不变。统计的结果是，UKF方案耗时约为EKF方案耗时的3倍左右，UKF-EKF方案耗时约为UKF方案耗时的70%左右。计算效率统计情况表明，UKF-EKF方案由于减省了采样次数、改进了系统弱非线性部分的处理策略，可比UKF方案提高约30%的计算效率。
4 结束语EKF算法是比较经典的卫星定轨算法，虽然得到了广泛应用，但它仍具有一定的理论局限性。针对EKF算法的缺陷，许多学者提出了一些改进算法，如自适应抗差滤波算法、UKF算法等。UKF算法虽然比EKF算法的估计精度要高，但耗时较多，计算效率较低，这在一定程度上制约了UKF算法的广泛应用。
本文提出的UKF-EKF算法，就是对UKF算法的一种改进与拓展。针对星载GPS卫星定轨的特点，UKF-EKF算法将UKF算法和EKF算法相结合，系统的强非线性部分采用UKF处理，弱非线性部分采用EKF处理，实际算例表明，UKF-EKF算法的估计精度与UKF算法基本相当，但计算效率提高了约30%，这对于某些实时或准实时应用而言，还是非常有效的。
随着卫星应用对卫星轨道的精度和时效性的不断提高，对卫观测手段也越来越丰富和多样化，数据处理方法也不再固守单一模式，如何针对系统模型的特点，设计更为有效的满足需求的算法，将是未来卫星定轨算法的发展趋势。
| [1] | LI Jisheng. Satellite Precision Orbit Determination[M]. Beijing: PLA Press, 1995. (李济生. 人造卫星精密轨道确定[M]. 北京:解放军出版社,1995.) |
| [2] | WEN Yuanlan. Spacecraft Precision Orbit Robust Estimation Theory and Application Research[D]. Zhengzhou: Information Engineering University, 2001. (文援兰. 航天器精密轨道抗差估计理论与应用的研究[D]. 郑州: 信息工程大学,2001.) |
| [3] | YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2/3): 109-116. |
| [4] | YANG Yuanxi, HE Haibo, XU Tianhe. On Adaptively Kinematic Filtering[J]. Acta Geodetica et Cartographica Sinica, 2001, 30(4): 293-298. (杨元喜,何海波,徐天河. 论动态自适应滤波[J]. 测绘学报,2001,30(4): 293-298.) |
| [5] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. |
| [6] | YANG Yuanxi, WEN Yuanlan. Synthetically Adaptive Robust Filtering for Satellite Orbit Determination[J]. Science in China: Earth Sciences, 2004, 47(7): 585-592. |
| [7] | JULIER S J, UHLMANN J K, DURRANT-WHYTEN H F. A New Approach for Filtering Nonlinear Systems[C]. Proceedings of the 1995 American Control Conference. Seattle: IEEE, 1995: 1628-1632. |
| [8] | LEE D J, ALFRIEND K T. Precise Real-time Orbit Estimation Using the Unscented Kalman Filter[J]. Advances in the Astronautical Sciences, 2003, 114: 1835-1854. |
| [9] | LIU Yang, PAN Xiaogang, WANG Zhengming, et al. An Augmented-GPS Based Adaptive UKF Method for Real-time Inter-satellite Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 15-22. (刘洋,潘晓刚,王正明,等. 基于增强型GPS的自适应UKF实时星间相对定位方法[J]. 测绘学报, 2008, 37(1): 15-22.) |
| [10] | JIANG Weinan, ZHOU Haiyin, DUAN Xiaojun, et al. UKF with Scaled Minimal Skew Simplex Sampling and Its Application in Satellite Orbit Determination[J]. Aerospace Shanghai, 2008, 25(5): 12-15. (姜伟南, 周海银, 段晓军, 等. 比例最小偏度单形采样的UKF及其在卫星定轨中的应用 [J]. 上海航天, 2008, 25(5): 12-15.) |
| [11] | LI Dan, LIU Jianye, XIONG Zhi, et al. Square Root Unscented Kalman Filter for Satellite Autonomous Navigation System Based on Minimal Skew Simplex Transformation[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(1): 54-58. (李丹, 刘建业, 熊智, 等. 基于最小偏度采样的卫星自主导航SRUKF算法[J]. 南京航空航天大学学报, 2009, 41(1): 54-58.) |
| [12] | PAN Quan, YANG Feng, YE Liang, et al. Survey of a Kind of Nonlinear Filters: UKF[J]. Control and Decision, 2005, 20(5): 481-489. (潘泉,杨峰,叶亮, 等. 一类非线性滤波器: UKF综述[J]. )控制与决策, 2005, 20(5): 481-489. |
| [13] | WU Jiangfei, HUANG Cheng. Unscented Kalman Filter and Its Application in GPS-based Satellite Orbit Determination[J]. Acta Astronomica Sinica, 2005, 46(1): 55-61. (吴江飞,黄珹. 分布逼近的卡尔曼滤波及其在星载GPS卫星定轨中的应用[J]. 天文学报, 2005, 46(1): 55-61.) |
| [14] | WU Jiangfei, HUANG Cheng. A Sampling-based Square Root Filter and Its Application[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 696-698. (吴江飞,黄珹. 一种采样型平方根滤波及其应用[J]. 武汉大学学报:信息科学版, 2007, 32(8): 696-698.) |
| [15] | WU Jiangfei, HUANG Cheng. Nonlinear Adaptively Robust Filter for Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 187-190. (吴江飞,黄珹. 非线性自适应抗差滤波定轨算法[J]. 武汉大学学报: 信息科学版, 2008, 33(2): 187-190.) |
| [16] | ROH K M, PARK S Y, CHOI K H. Orbit Determination Using the Geomagnetic Field Measurement via the Unscented Kalman Filter[J]. Journal of Spacecraft and Rockets, 2007, 44(1): 246-253. |
| [17] | JULIER S J. The Scaled Unscented Transformation[C]//Proceedings of the 2002 American Control Conference. Jefferson City: IEEE, 2002: 4555-4559. |
| [18] | JULIER S J, UHLMANN J K. Reduced Sigma Point Filters for the Propagation of Means and Covariance through Nonlinear Transformations[C]//Proceedings of the 2002 American Control Conference. Jefferson City: IEEE, 2002: 887-892. |
| [19] | YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650. (杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650.) |