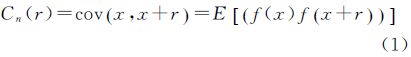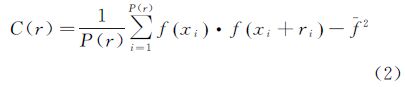2. 西部矿产资源与地质工程教育部重点实验室,陕西 西安 710054
2. Key Laboratory of Western China’s Mineral Resources and Geological Engineering,Ministry of Education,Xi’an 710054,China
1 引 言
合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)是近几十年迅速发展起来的一种能够精确测定地表三维信息和高程变化信息的微波遥感新技术。它具有高分辨率、高覆盖和不受区域环境与气候约束的特征,能较好地解决传统地表形变观测中三维空间上由于人工布设观测点获取的形变信息量不足和恶劣区域信息采集困难等问题[1, 2],故可获取更多的形变信号和揭示更多的地球物理现象,为地球物理反演研究提供一种全新的途径,因此InSAR被众多学者认为是一种极具潜力的空间对地观测新技术[3]。然而,由于InSAR获取的是基于像素的连续面状形变数据,其包含的数据量较大,不但包含了大量冗余数据,而且还包含不少强噪声和伪信号等,这些冗余数据和粗差噪声不仅影响数据后处理的计算效率,而且还会因误差的存在对InSAR结果解译和形变机理反演等的可靠性带来极为不利的影响[4]。因此,在保持形变信息基本特征不变的前提下,在有效地压缩InSAR数据量的同时能消除一定的噪声影响,是InSAR数据后处理的重要任务之一[5]。
无论何种影像的数据压缩都应遵循尽可能保留原数据的基本特征信号的原则。常用的影像压缩算法是通过将影像变换到频率域或小波域[6, 7, 8, 9],通过仅存储小部分的频域或小波系数来达到影像压缩的目的,但是这类方法是对数据存储大小的压缩而非数据量大小本身的压缩。而基于InSAR形变结果的反演研究则需要对数据量本身进行压缩,因此,这类方法并不适用。针对此,文献[10]提出了InSAR数据点的规则采样法,该方法计算简单,但需要在数据压缩率和形变细节间进行取舍。文献[4, 11]分别利用象限分解的方法实现InSAR数据的重采样以达到数据压缩目的。文献[12]则提出了基于像素分辨率的InSAR数据减采样方法。这些方法均能在一定程度上达到InSAR数据量的有效压缩,但其更多的是针对地震、火山等大尺度形变,需设定某些形变震源参数等,不具有普适性。基于此,本文将四叉树分解法引入InSAR监测数据的压缩中,四叉树分解是一种基于均匀性检测的图像分割算法[13, 14];同时,考虑到InSAR数据自身误差的特点,本文提出了顾及InSAR监测数据的物理空间相关性设定协方差函数对四叉树分解中的参数进行设定的方法,提高了算法的可靠性。这种顾及协方差函数的自适应四叉树压缩算法在较好保持形变信息的同时,可对数据量进行有效的压缩,且能在一定程度上达到噪声消除的目的,具有较好的普适性。
本文提出的InSAR数据压缩算法,主要针对InSAR相位监测数据进行分析,该数据既可是解缠相位,也可是经过地理编码等转换后的形变数据,算法具有通用性。本文主要以InSAR解缠相位数据为例进行算法的解释和分析。
2 四叉树InSAR数据压缩在形变模型反演中,为获取最优的模型参数,常常需要采用非线性迭代法进行大量的模型预测估计。而基于像素的连续面状覆盖的InSAR变形监测数据,则含有成千上万数以百万计的数据点,其中包含了大量的冗余数据和强噪声等引起的误差乃至粗差等,利用这些形变数据点反演需要进行成千上万次的模型迭代估计,这无疑给模型的解算带来了不可估量的计算困难和负担,而且异常噪声的存在,将导致反演结果的严重失真[12]。因此有必要在尽可能地保持形变重要细节信息不变的条件下,寻求合适的InSAR变形监测数据压缩算法,这是InSAR数据后处理和形变模型反演研究的一个重要内容。本文研究将自适应四叉树分解方法引入InSAR数据压缩,该算法可在保持形变基本特征信息的同时,对数据量进行有效的压缩。
2.1 四叉树分解原理四叉树分解是一种基于均匀性检测的图像分割算法。自适应四叉树分解,则是为了以最少的数据量,得到各个像块的均值,从而获得对原始图像的最佳逼近[13]。对影像进行四叉树分解的基本流程为:首先通过添加零值将影像的维数扩充为2的幂次,四叉树分解要求影像的大小为N=2n,其中,n为正整数,N为影像的维数。然后将影像分成大小相等的4个象限,分别计算各个象限内解缠值的方差,并将其与预先设定的方差阈值进行比较,若某象限方差超过阈值,则将该象限进一步分解为4个新的象限;重复上述过程直到收敛,即各个象限方差均小于给定的阈值;最后将分解后的各个象限的均值或中值赋给象限的中心坐标,仅保留该象限中心坐标点即可[15]。
2.2 算法的优缺点分析四叉树压缩算法的主要优点是可在形变梯度变化较大处保留较多数据点,而在数据平坦即连续处保留较少点,因此相较于常规的规则降采样等方法,它能更好地在保留形变细节信息不损失的同时,还可实现有效的数据压缩;同时由于采用均值算法为象限赋值,其本质上也是一种低通滤波,可有效地消除影像中噪声占主导地位的高频部分,实现噪声消除。但是,该算法也有不足之处:若某个分解象限内的形变值整体具有较好的一致性而仅在某个较小的区域内存在形变特征,尽管该小形变区域内的方差可能会明显高于给定的方差阈值,但由于该象限整体的方差值比分解阈值低很多,在最后运算时仅将一个值赋给该象限的中心坐标,从而忽略该小形变区域,易造成形变细节信息的损失。为解决该问题,本文在进行四叉树分解时,通过设定最大象限大小参数对其进行改进。
结合以上可知,在进行四叉树分解时,需确定两个重要参数:象限分解阈值和最大象限大小。这两个参数的确定,需要对数据噪声的统计特性进行分析,为此,本文引入噪声协方差函数进行计算。
3 InSAR噪声协方差函数估计由于大气和电离层等影响通常在数十到数百千米的尺度范围内是相关的,且和高程相关的大气水汽变化也会引起和地形相关的卫星视向信息延迟等[16],因此InSAR获取的干涉信号中存在空间相关信息[17],在测量中,这些信号被认为是观测噪声,而且这些噪声的空间相关度同样会影响InSAR监测数据的质量。为有效地利用InSAR观测结果进行形变机理的反演和比较等,必须对这些噪声信号进行估计和去除。特别在InSAR监测数据中的这种相关性,更主要地表现为一种物理空间相关,不能直接用函数拟合等简单的数学模型构建,对于此,本文给出了利用协方差函数对这些噪声信号进行估计和分析的方法。
在进行噪声协方差函数Cn估计时,假设噪声满足二阶平稳且各向同性,即两点间的协方差仅与其距离相关而和点的位置及方向无关。设r为两点间距离,则其协方差可表示为
式中,r=|r|;f(x)为干涉图中x处的值,且假设噪声的均值为0。协方差函数的计算通常有两种方法[12],一种是参照变异函数的计算,利用一个简单的经验协方差函数式求解
式中,P(r)为距离r的点对数目;f(xi)和f(xi+ri)为影像在xi和xi+ri处的取值;y为影像的局部均值。另一种则是根据二维自相关计算。在利用二维自相关计算协方差时,首先需对数据中的无效值进行0值填充,然后利用功率谱的逆傅里叶变换计算二维自相关,最后利用二维自相关的旋转平均值计算一维协方差。在频域中会在影像的边界处引入常数变化,但是由于影像的均值为0,其基本上是正负相抵的,故可忽略。唯一需要的是利用数据中的非0点数对功率谱进行加权以使自相关正则化。影像gij的功率谱可通过离散二维傅里叶变换Gkl计算
式中,Gkl为gij的二维离散傅里叶变换;Gkl*为Gkl的共轭;Nnz为gij中的有效值个数。求得自相关后,即可利用二维自相关函数的旋转平均值估计一维协方差函数。如图 1所示即为利用二维自相关计算协方差函数的流程图。
|
| 图 1 利用二维自相关计算协方差函数流程 Fig. 1 Covariance function calculation based on 2D autocorrelation |
协方差函数给出的是一个两点间相似性的测度,当两点间的距离大于某个特定值时,协方差值趋于0,表明当两点间的距离大于该特定值时,数据点间不相关。
4 算法的实现在求取噪声协方差函数时,仅关心噪声的统计特性,故需要分离进行形变信息和噪声的估计,可通过分析干涉条纹确定可能的形变区域,再利用掩膜处理将该区域形变从干涉图中去除;另外,干涉图中通常还含有因干涉基线估计不正确所引起的轨道残余误差[18, 19],由于轨道误差通常呈现为明显的线性趋势分布,故可利用线性拟合估计的方法提取一个最佳拟合平面将其剔除[20]。由此,可认为剩余的信息即为局部均值接近于0的噪声数据,则可利用文中上节提到的方法进行噪声协方差函数的估计。
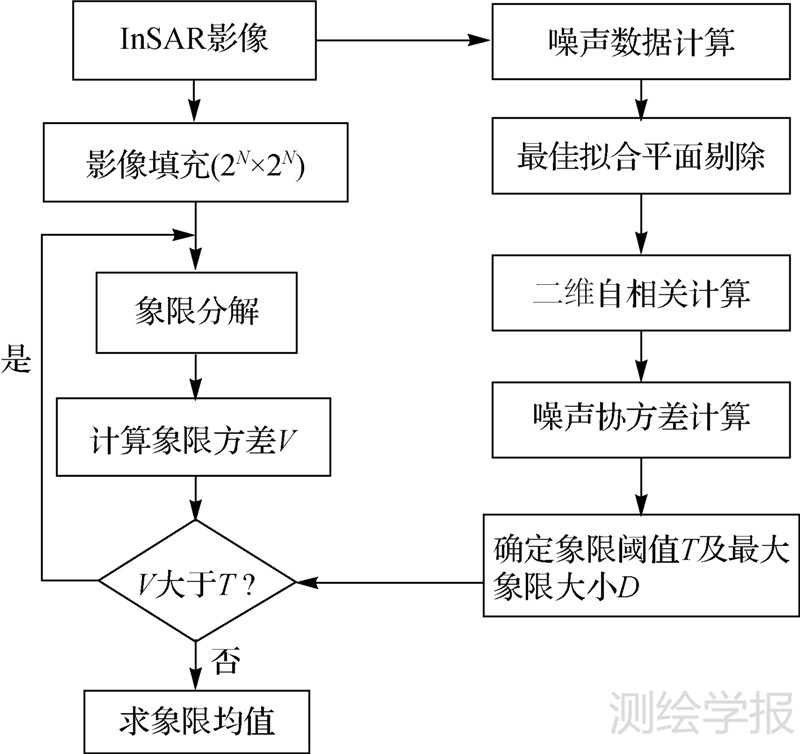
由估计的噪声协方差函数即可确定四叉树分解的两个重要参数:象限分解阈值和最大象限大小。象限分解阈值原则上应远大于噪声方差,但足够小以保留形变细节特征不损失,通常可取4倍噪声方差;最大象限大小可设为影像中使数据点间不相关的距离。这两个参数都可以根据估计的噪声协方差函数确定。利用确定的参数,采用四叉树对InSAR数据进行分解:即当某个分解象限的形变方差小于给定阈值时,将该象限内影像的均值赋给该象限中心坐标,在数据输出时仅保留该象限中心值。图 2即为本文算法的完整流程图。
|
| 图 2 顾及协方差函数的InSAR数据四叉树压缩算法流程图 Fig. 2 Flow chart of the quadtree InSAR data reduction method based on covariance function |
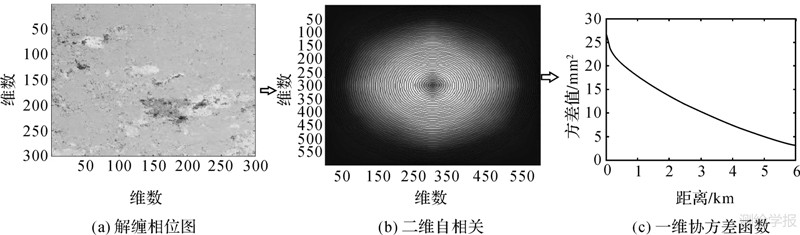
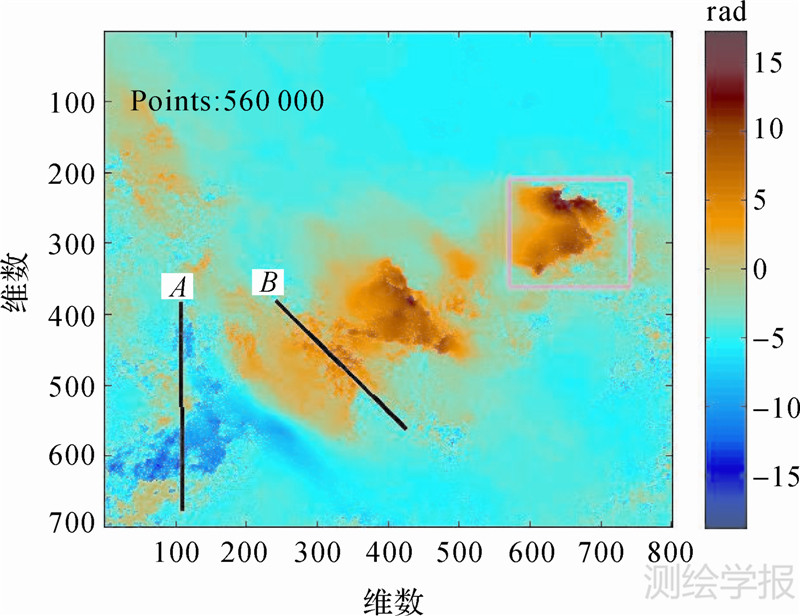
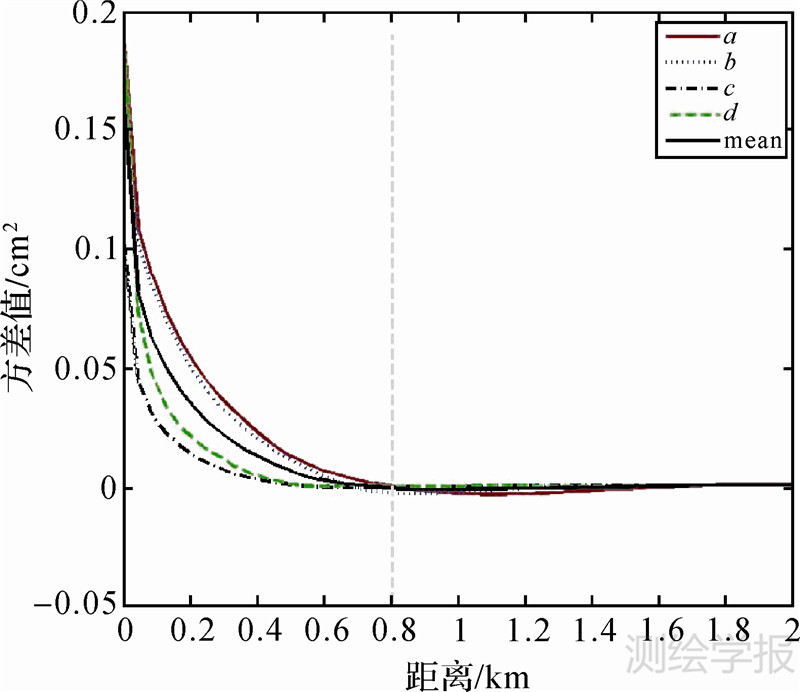
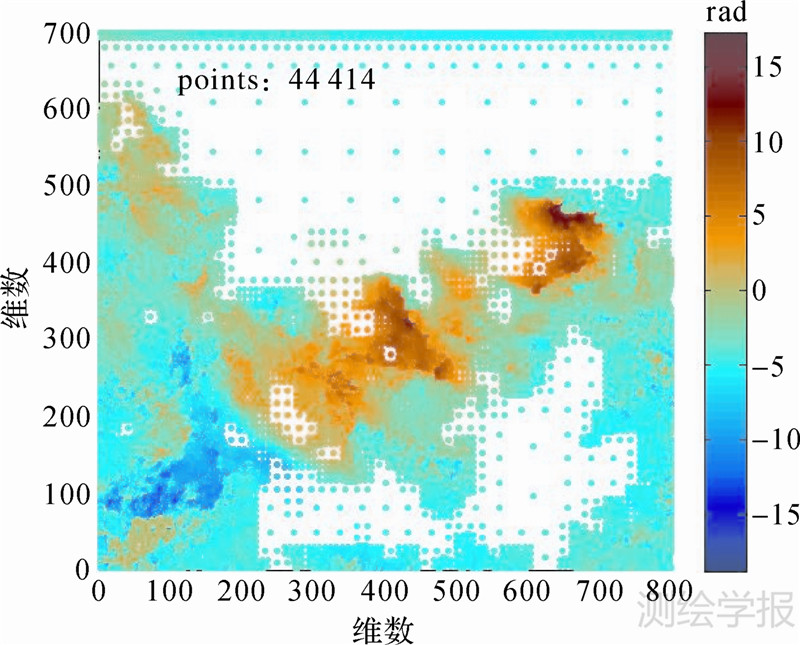
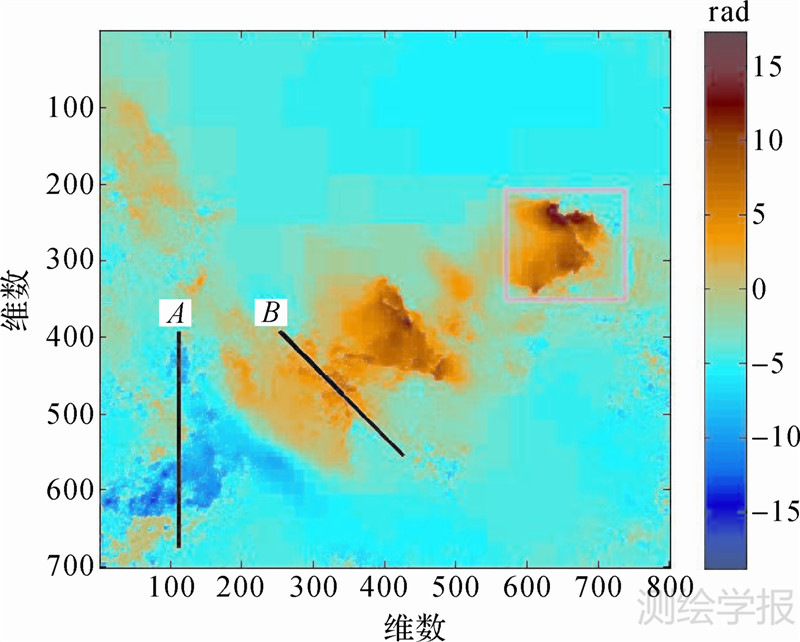
本文以西安地区的InSAR解缠相位数据为例进行了试验分析,图 3即为研究区解缠干涉图,其中形变发生的主要区域为西安的高新开发区,其沉降量级约为10 cm左右。图 4为利用二维自相关估计的噪声协方差函数,从该协方差函数可看到,最大噪声方差约为0.18 cm2,取四叉树分解阈值为4倍噪声方差,即0.72 cm2。进一步从图上可看到,当点间距离大于0.8 km时,协方差函数接近于0,认为数据点间不相关,故可取象限的最大距离为0.8 km,即最大象限的面积为(0.64 km2)。考虑到影像的像素大小为20 m,相当于40个像素大小,故取最大象限为64(需为2N)。图 5为利用四叉树压缩算法提取的数据散点图,其数据量从原始的560 000个点降为44 414个点,压缩后的数据量仅约为原数据的7.93%。从图上可看到在形变发生区数据点采样密集,充分保留了形变的细节特征信息量,而在数据变化平缓或无形变处仅保留了少量的数据点,从而大大地降低了数据的量级;且利用四叉树压缩数据能够很好地对原数据进行重构,如图 6所示,利用四叉树压缩数据得到的解缠图很好地保留了原解缠图的形变细节信息,且相较于原图其连续性更好,在部分噪声明显区域进行了有效的噪声消除。为进一步比较四叉树压缩算法的效果,对图 3和图 6中小框内的区域分别进行放大显示,结果如图 7和图 8所示。
|
| 图 3 西安解缠影像 Fig. 3 Unwrapping image of Xi’an |
|
| 图 4 协方差函数 Fig. 4 Covariance function |
|
| 图 5 四叉树分解数据点图 Fig. 5 Scatter points of Quadtree decomposition |
|
| 图 6 四叉树压缩数据重构影像 Fig. 6 The image by quadtree reduction data |

|
| 图 7 裁剪区原影像 Fig. 7 Sub-image of the full image |

|
| 图 8 裁剪区四叉树分解影像 Fig. 8 Quadtree decomposition image of the sub-image |
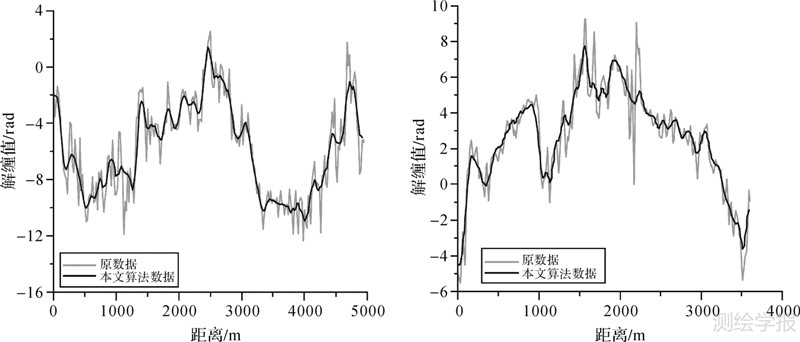
从图 7和图 8的研究区域放大视图可看出,其很好地保留了形变信号的细节信息,几乎无细节损失,但数据点数却降低了2~3个数量级,可有效地提高后续模型优化反演等操作的运算效率。另外,通过对图 7和图 8的观察分析可看到,利用顾及协方差的四叉树压缩算法得到的解缠图噪声明显变小,相位变化连续性更好。为对比说明本文方法的效果,进一步提取了图 3和图 6中的两条剖线A和B进行分析,结果如图 9所示,从剖线图上可更直观地看到利用该算法在一定程度上对数据中的部分噪声进行了有效消弱,数据整体更光滑,达到了噪声消除的目的。
|
| 图 9 研究区剖线分析(左为剖线A,右为剖线B) Fig. 9 Profile analysis of the area |
本文提出了顾及InSAR数据物理空间相关特性设立协方差函数的自适应四叉树分解InSAR数据压缩算法,并以西安地区的InSAR解缠相位数据为例进行了试验分析,充分地证明了该算法的有效性。从结果可看到,该算法能够在形变变化明显处进行密集采样,而在形变变化平坦处进行稀疏采样,从而能够在较好地保留InSAR数据的细节信息不损失的条件下,达到有效的InSAR数据量压缩目的,使InSAR数据点的数量降低2~3个量级,能有效地提高后续模型优化反演等操作的运算效率,大大节省计算时间和硬件损耗;同时,由于采用了均值运算作为四叉树分解的算子,在保证了该算法为线性的条件下,可有效地消除数据中的部分高频噪声,减小相位的突变,使数据整体连续性增强,数据更加平滑。
| [1] | FERRETTI A, MONTI G A, PRATI C, et al. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation[M].AG Noordwijk: ESA Publications,2007. |
| [2] | LUO Haibin, HE Xiufeng, LIU Yanxiong. Estimation of Three-dimensional Surface Motion Velocities Using Integration of DInSAR and GPS[J]. Acta Geodaetica et Cartographica Sinica,2008, 37 (2): 168-171. (罗海滨,何秀凤,刘焱雄.利用DInSAR和GPS综合方法估计地表3维形变速率[J].测绘学报,2008,37 (2): 168-171.) |
| [3] | LIU Guoxiang. Surface Deformation Monitoring with Radar Interferometry[M].Beijing:Surveying and Mapping Press,2006.(刘国祥.利用雷达干涉技术监测区域地表形变[M]. 北京: 测绘出版社, 2006.) |
| [4] | JONSSON S. Modeling Volcano and Earthquake Deformation from Satellite Radar Interferometric Observations,[D].California: Stanford University, 2002. |
| [5] | ZHANG Jing, ZHAO Chaoying, ZHANG Qin,et al. Research on Deformation Contour Mapping from Interferometry[J]. Journal of Geodesy and Geodynamcs,2009,29(5):143-146.(张静,赵超英,张勤,等.InSAR形变等值线图绘制方法研究[J].大地测量与地球动力学,2009,29(5):143-146.) |
| [6] | DU Xutao. Discussed on the Image Compression Algorithm Based on Transformation[J]. Software Guide, 2012,11(1):145-148.(独旭涛. 基于变换的图像压缩算法探讨[J]. 软件导刊,2012,11(1):145-148.) |
| [7] | LI Sha, HUANG Lin,ZHOU Jianqi, et al. SAR Image Compression Algorithm Based on Wavelet Transform[J]. Computer Measurement and Control,2012,20(8):2310-2313.(李莎,黄琳,周剑奇,等. 基于小波变换的SAR图像压缩算法研究[J]. 计算机测量与控制,2012,20(8):2310-2313.) |
| [8] | XIE Haihui. Speckle Reduction and Data Compression in SAR Images Using Wavelet-Based Method[D]. Chengdu: University of Electronic Science and Technology, 2004.(谢海慧. 干斑抑制及图像压缩的小波域方法[D]. 成都:电子科技大学,2004.) |
| [9] | WELSTEAD S T. Fractal and Wavelet Image Compression Techniques[D].Washington: SPIE Optical Engineering Press, 1999,232. |
| [10] | PRITCHARD M E, SIMONS M, ROSEN P A, et al. Co-seismic Slip from the 1995 July 30 Mw = 8.1 Antofagasta, Chile, Earthquake as Constrained by InSAR and GPS Observations[J].Geophysical Journal International,2002,150(2): 362-376. |
| [11] | SIMONS M, FIALKO Y, RIVERA L. Coseismic Deformation from the 1999 Mw 7.1 Hector Mine, California, Earthquake as Inferred from InSAR and GPS Observations[J].Bulletin of the Seismological Society of America,2002,92:1390-1402. |
| [12] | LOHMAN R B, SIMONS M. Some Thoughts on the Use of InSAR Data to Constrain Models of Surface Deformation: Noise Structure and Data Downsampling[J]. Geochemistiy,Geophysics,Geosystems, 2005, Q01007. DOI:10.1029/2004GC000841. |
| [13] | NI Lin. Compression of Remote Sensing Images Based on Adaptive Quadtree Partitioning [J].Journal of Remote Sensing, 2002, 6(5):343-351.(倪林.基于自适应四叉树分割的遥感图像压缩算法[J]. 遥感学报,2002,6(5):343-351.) |
| [14] | LIU Yang, GONG Adu, LI Jing. A Model for Massive 3D Terrain Simplification Based on Data Block Partition and Quad-tree[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):410-415. (刘扬,宫阿都,李京. 基于数据分层分块的海量三维地形四叉树简化模型[J]. 测绘学报, 2010, 39(4):410-415.) |
| [15] | HE Xingheng, CHEN Hui.Method Based on Quarter-tree Decomposition of Image Compression[J]. Computer Engineering and Applications, 2008,44(9):181-183.(何兴恒,陈慧.一种基于四叉树分解的图像压缩方法[J].计算机工程与应用,2008,44(9):181- 183.) |
| [16] | WAN Qing, ZHANG Lu, JIANG Houjun, et al. Estimation and Removal of Atmospheric Effects in InSAR Topographic Mapping[J]. Journal of Remote Sensing,2012, 16(5):1074-1088. |
| [17] | KNOSPE S H G, JONSSON S. Covariance Estimation for DInSAR Surface Deformation Measurements in the Pressence of Anisotropic Atmospheric Noise[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010,48: 2057-2065. |
| [18] | JI Lingyun, WANG Qingliang, CUI Duxin,et al. Influence of SAR Orbital Data to the Accuracy of DEM by Doris[J]. Science of Surveying and Mapping, 2009,34(5): 57-59. (季灵运,王庆良,崔笃信,等.SAR卫星轨道数据精度对Doris获取DEM精度的影响研究[J]. 测绘科学,2009,34(5):57-59.) |
| [19] | JIN Guowang, WU Yirong,XIANG Maosheng, et al. Baseline Estimation Algorithm of InSAR with Block Adjustment[J].Acta Geodaetica et Cartographica Sinica, 2011,40(5): 616-622.(靳国旺, 吴一戎, 向茂生,等. 基于区域网平差的InSAR基线估计方法[J].测绘学报,2011,40(5): 616-622.) |
| [20] | HETLAND E A, MUSÉ P, SIMONS M, et al. Multiscale InSAR Time Series(MInTS) Analysis of Surface Deformation[J] Journal of Geophysical Research,2012,117,B02404. DOI:10.1029/2011JB008731. |