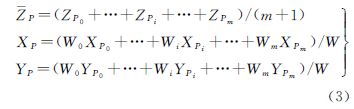1 引 言
机载激光探测与测距(airborne light detection and ranging,机载LiDAR)是一项集成激光扫描仪和定位定姿系统(position and orientation system,POS)的三维地形数据快速获取技术。通过在机载LiDAR设备上搭载数码相机,可同步获取具有很强互补性[1]的LiDAR点云和高分辨率彩色航空影像。两种数据的集成在三维建模以及正射影像制作等领域有着广泛应用[2]。然而由于相机多为临时安置,其与POS设备之间的安置角很难准确测量[3],导致由POS数据计算获得的影像外方位元素精度不高,为此仍需对航空影像进行区域网空中三角测量解算影像的准确外方位元素[4, 5]。
航空影像区域网空中三角测量中一个重要步骤是影像间连接点自动匹配[6, 7, 8]。目前在摄影测量领域常采用SIFT(或SURF以及其他尺度与旋转不变性特征)匹配、相关系数匹配、最小二乘匹配等算法以及金字塔影像匹配、仿射变换纠正等策略以获取高精度匹配点[9, 10, 11, 12, 13, 14, 15]。为缩小影像匹配过程中同名点搜索范围,还可利用有理多项式模型、POS数据等建立几何约束条件辅助影像匹配[16, 17, 18]。由于机载LiDAR数据采集中,常会出现多个航高、交叉飞行的航带,还需采用POS数据恢复影像间的重叠关系。文献[18]提出了POS辅助航空影像自动转点方法,取得了很好的匹配结果,但需采用地面检校场对POS系统进行检校,在检校场布置较困难的地区应用受到制约。有研究表明POS数据的主要误差源在角元素中[19],而角元素的误差主要来源于相机安置角误差[3]。目前已有一些无需真实地面控制点、结合LiDAR数据进行相机安置角误差检校的方法[3, 20],但在自动化程度和效率上不适合在影像匹配之前进行安置角误差快速检校。
鉴于对机载LiDAR设备搭载的数码相机同步获取的影像进行匹配时,可将同步获得的较高精度LiDAR点云数据生成数字表面模型(digital surface model,DSM)进行物方约束的影像匹配[7, 21],故本文研究了LiDAR点云和POS辅助航空影像连接点自动匹配方法。从基于物方约束的影像匹配原理出发,研究了快速相关系数匹配算法,并采用一种基于虚拟地面控制点的相机安置角误差快速检校方法提高影像外方位元素精度,在检校基础上自适应确定影像匹配搜索范围,无需对影像进行排航带、旋转、畸变纠正等操作即可自动进行匹配。研制了相应的点云和POS辅助航空影像连接点自动匹配软件。采用8条航带共62张航空影像及相应LiDAR点云进行试验,验证了本文算法的有效性。
2 LiDAR点云和POS辅助航空影像连接点自动匹配原理本文从基于物方约束的影像匹配原理出发,先进行基于虚拟地面控制点的相机安置角误差检校,在优化影像外方位元素精度后进行测区内所有影像的连接点自动匹配。在匹配过程中,采用快速相关系数匹配算法加快同名点搜索速度。相关算法原理如下。
2.1 物方约束匹配原理及快速相关系数匹配算法 2.1.1 基于物方约束的航空影像匹配基本原理本文将与航空影像同步获取的LiDAR点云按一定的间隔(取点云平均间距)采样生成DSM,结合POS数据,进行物方约束的航空影像连接点匹配。方法如下:①依次将每张影像当做参考影像,提取特征点,对于参考影像上的特征点,依据共线条件方程将其投影到DSM上,获得该点对应的概略物方坐标;②采用文献[18]提出的POS辅助同名像点位置预测以及待匹配窗口影像的几何变形改正方法,获得特征点在所有相邻待匹配影像上的搜索区;③在参考影像与待匹配影像之间进行两级金字塔影像相关系数匹配,获取准确匹配点位,并采用最小二乘匹配方法精化匹配结果。
2.1.2 快速相关系数匹配算法传统的相关系数影像匹配需在搜索区逐点计算相关系数,考虑到影像上相邻像素点的灰度具有一定的连续性,相应的相关系数值也应具有一定连续性。图 1为某特征点在对应匹配搜索区上的相关系数示意图(相关系数小于0时设为0),用灰度表示点位处的相关系数值。图中将相关系数值从0到1依次按从白到黑显示,颜色越黑表示相应点位处相关系数值越大。从图 1可见在最佳匹配点位(灰度最黑的点位)附近存在一片相关系数值连续区域。据此,设计如下用于相关系数匹配的最佳匹配点位快速搜索算法(简称快速相关系数匹配):首先,在图 2中格网所示的搜索区(共有16×16=256个搜索点位,以图 2中左上角5×5格网为一个基本单元对搜索区进行划分)中先逐个计算黑色点位处的相关系数值,找出相关系数大于阈值T1的所有点位;其次,判断以上点位八邻域内还未参与计算的格网处是否存在相关系数大于阈值T1的点位,如有则继续对这些点位八邻域的格网点进行分析,直至不再有新的相关系数大于阈值T1的点位出现;最后,统计所有参与计算的点位处相关系数最大值,若其大于阈值T2,以最大值对应的点位为最佳匹配点位。

|
| 图 1 某特征点在影像匹配搜索区上的相关系数示意图 Fig. 1 Illustration of correlation coefficient values between matching window and searching window |

|
| 图 2 相关系数匹配最佳匹配点位快速搜索算法示意图 Fig. 2 Illustration of fast searching algorithm for obtaining conjugate point in correlation matching |
该算法优势在于,对于图 1所示的大片相关系数为0的白色区域,只需通过在较稀疏的点位上进行计算即可自动跳过这一区域,无需逐点进行相关系数计算。对于图 2所示搜索区中任何一个白色格网点,在其周围四个方向上(上下、左右及两个对角方向)最少相邻1个像素、最多相邻2个像素均有在第一次搜索中参与计算的点位,无论该点的灰度值与周围像素在哪一方向上连续,只要该点的相关系数足够大,均可保证该点最终被搜索到。将本算法应用到2.1.1 节的最上层金字塔影像匹配中,可节省计算量。在后文的试验部分将通过试验分析阈值T1与T2取值。
2.2 基于虚拟地面控制点的相机安置角误差检校及匹配搜索范围自适应确定 2.2.1 基于虚拟地面控制点的相机安置角误差检校本文提出一种虚拟地面控制点计算模型,在对其理论分析基础上设计了一种基于虚拟地面控制点的相机安置角误差检校算法:
首先,进行基准片匹配。结合POS数据与DSM,自动选择位于测区中间、地势较平坦且非纹理贫乏区域(如无大面积水体、植被覆盖的区域)的一张影像作为基准片影像,采用物方约束影像匹配方法将该基准片与所有相邻影像进行连接点自动匹配,并进行匹配点粗差剔除。由于受相机安置角误差的影响,预测点位偏差较大,在匹配时需要设置较大的同名点搜索范围。
然后,根据下文方法计算虚拟地面控制点的近似物方坐标值。
最后,进行外方位元素修正。在获取的虚拟控制点的数目足够且在基准片上分布均匀的情况下,采用全部虚拟控制点对基准片进行单片空间后方交会,在固定外方位线元素的条件下修正外方位角元素。在对基准片进行外方位角元素修正后,根据式(1)计算相机安置角误差补偿矩阵Rrot,然后根据公式(2)修正测区内所有影像的外方位角元素
式(1)、式(2)中,R1为改正前影像外方位角元素构成的旋转矩阵;R2为经过相机安置角误差改正后的外方位角元素组成的旋转矩阵;Rrot为相机安置角误差补偿矩阵。本文采用下述方法计算虚拟控制点的近似物方坐标。从位于地形局部平坦处的航带间4°及以上重叠加密点(在每航带内至少有2°重叠)中选择虚拟控制点,假设某一加密点P的理想地面坐标为(XPi,YPi ,ZPi)(影像外方位元素无误差的情况下的投影点位),其在各影像上的像点为pi (i=0,1,2,…,m; m≥3)。首先,采用影像初始外方位元素将各像点pi投影到DSM上,分别获得对应的物方点Pi(XPi,YPi ,ZPi),通过比较各ZPi的最大值与最小值的差值是否小于阈值(设置为1.0m)判断投影点是否位于地形局部平坦处,如是则将该加密点作为一个虚拟地面控制点。然后,按式(3)计算点P的近似物方平面坐标值(XP,YP)
式中,Wi(i =0,1,2,…,m; m≥3)为各影像对应投影点的权值;W=W0+…+Wi+…+Wm。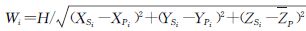 式中,XSi、YSi、ZSi为影像i的摄影中心坐标;H=ZS0-ZP0为概略航高。在计算各影像相应投影点的权值时,考虑到各物方投影点Pi的高程坐标ZPi差别较小,故均用均值ZP代替。在计算出点P的近似物方平面坐标值(XP,YP)后再在点云中内插出该位置的高程值作为点P的近似高程值ZP。
式中,XSi、YSi、ZSi为影像i的摄影中心坐标;H=ZS0-ZP0为概略航高。在计算各影像相应投影点的权值时,考虑到各物方投影点Pi的高程坐标ZPi差别较小,故均用均值ZP代替。在计算出点P的近似物方平面坐标值(XP,YP)后再在点云中内插出该位置的高程值作为点P的近似高程值ZP。
下面分析上述计算获得的P点的坐标(XP,YP ,ZP)相对于单张影像投影获得的地面点坐标(XPi,YPi ,ZPi)(i =0,1,2,…,m; m≥3)的精度(由于位于局部平坦处,为方便分析,此处可近似认为ZPi=ZP=ZP=ZPt,故仅需分析平面精度)。假设P点为位于S0、S1、S2、S3 4张影像上的航带间4°重叠点,S0、S1位于第一航带,S2、S3位于第二航带,第一航带和第二航带的飞行方向相反(影像飞行路线为S0—S1—S2—S3)。假设3个角元素的误差分别为Δφ、Δω、Δκ,图 3分别为Δφ、Δω及Δκ对投影点的平面坐标的影响示意图。从图 3(a)和图 3(b)可见对于航带间重叠影像S1和S3,由于飞行方向相反,导致Δφ(或Δω)对两影像作用相反,使得投影点P1、P2与理想投影点P的偏移量相反;从图 3(c)可见Δκ亦对航带间影像投影点的平面坐标值造成相反的偏移量。由于Δφ、Δω及Δκ均为小角,可近似认为3幅图中偏移量分别为Δφ|SiP|、Δω|SiP|和Δκ|SiP|,即离该地面点距离越近的影像,其投影获得的地面点坐标值受安置角误差的影响越小,地面点精度相对越高,故在式(3)中其权值应越大。需说明的是,以上分析中的距离均为在投影面上的平面距离,由于其分别几乎与相应的三维空间距离成正比,故在计算权值时统一由摄影中心到地面点的三维距离代替。

|
| 图 3 3个角元素误差分量对投影点的平面坐标影响示意图 Fig. 3 The affection of three angular elements errors to the horizontal coordinates of the projected ground point |
本文在进行相机安置角误差检校并更新影像外方位元素的基础上,提出了同名点搜索范围自适应确定方法。其原理如下:①对于基准片匹配获得的加密点,将基准片上的像点投影到DSM上,获取每一个像点对应的物方坐标值;②将获得的物方坐标值反投影到每张重叠影像上,分别计算投影点位与匹配点位的差值,并统计点位差值中误差DRMS;③在对所有影像进行连接点匹配过程中,将特征点投影到DSM上获取其物方坐标的同时,判断该点所处位置是否平坦。如果该点位于平坦处,匹配搜索范围取4倍DRMS大小的窗口,否则,如果该点处于不平坦区域,预测点位误差可能较大,相应的搜索范围取6倍DRMS大小的窗口。
3 试验与分析 3.1 试验数据基于以上匹配算法,开发了LiDAR点云和POS数据辅助航空影像匹配软件,采用某试验区的LiDAR点云、POS数据和航空影像进行了影像连接点匹配试验。试验区为城区,如图 4所示共有8条航带62幅航空影像,以及同步获取的8个条带LiDAR点云,其中包括东西飞行的5条航带和南北飞行的3条航带(影像7-13与影像28-34所在航线重叠)。试验数据由Trimble H68机载扫描仪获取,相机的像元大小为0.006mm,焦距为51.71mm,影像像幅大小为8984像素×6732像素。东西飞行影像航向重叠度为60%,旁向重叠度为60%,飞行高度为750m,影像地面分辨率为0.08m;南北飞行的影像航向重叠度为68%,旁向重叠度为69%,飞行高度为1050m,影像地面分辨率为0.12m。LiDAR点云平均点间距约为0.7m,点云高程精度约0.2m。试验计算机配置为Intel双核处理器,频率2.53GHz,内存2GB。

|
| 图 4 试验区正射影像及航线分布图 Fig. 4 The orthoimage and distribution of flight line of the test site |
为分析快速相关系数匹配算法的匹配效果,分别选择两组影像进行匹配试验。对于每一组影像首先采用传统的搜索区逐点搜索法进行匹配,将匹配结果作为参考值。然后采用本文提出的快速搜索算法,分别取T1为0.01、0.1、0.2、…、0.6,统计漏匹配加密点数、漏匹配像点数、误匹配像点数以及匹配耗时,试验结果如表 1所示。试验中影像相关窗口大小为19像素×19像素,影像搜索范围大小为59像素×59像素(不包括相关窗口尺寸),T2值统一取0.7。
| 测试数据 | 像对数 | 策略 | T2值 | T1值 | 加密点数 | 像点数 | 漏匹配加密 点数 | 漏匹配 像点数 | 误匹配 像点数 | 匹配时间/s |
| A | 41 | 传统算法 | 0.7 | - | 1257 | 13571 | - | - | - | 960.484 |
| 快速算法 | 0.01 | 1257 | 13571 | 0 | 0 | 0 | 861.234 | |||
| 0.1 | 1257 | 13571 | 0 | 0 | 0 | 788.828 | ||||
| 0.2 | 1257 | 13570 | 0 | 1 | 0 | 729.722 | ||||
| 0.3 | 1257 | 13560 | 0 | 11 | 0 | 680.266 | ||||
| 0.4 | 1254 | 13511 | 3 | 60 | 1 | 647.718 | ||||
| 0.5 | 1252 | 13376 | 5 | 195 | 10 | 626.375 | ||||
| 0.6 | 1232 | 12921 | 25 | 650 | 84 | 609.141 | ||||
| B | 41 | 传统算法 | 0.7 | - | 1089 | 10279 | - | - | - | 767.563 |
| 快速算法 | 0.01 | 1089 | 10279 | 0 | 0 | 0 | 720.703 | |||
| 0.1 | 1089 | 10277 | 0 | 2 | 0 | 686.562 | ||||
| 0.2 | 1089 | 10276 | 0 | 3 | 0 | 641.859 | ||||
| 0.3 | 1088 | 10271 | 1 | 8 | 0 | 609.985 | ||||
| 0.4 | 1087 | 10240 | 2 | 39 | 1 | 590.437 | ||||
| 0.5 | 1085 | 10120 | 4 | 159 | 10 | 574.641 | ||||
| 0.6 | 1070 | 9725 | 19 | 554 | 87 | 563.047 |
从对以上82个像对的匹配试验结果可见,随着T1值的增大,错误匹配数增多,而匹配耗时逐渐减少。当T1取0.4时错误匹配数仍然可忽略,综合考虑匹配错误率与匹配耗时,本文匹配时取T1为0.3。从表 1可知,在取T1为0.3时平均每对同名像点可节省匹配时间0.02s,与传统算法平均每对同名像点匹配耗时0.08s相比,节省了25%的匹配耗时。由于本试验采用物方匹配,对影像进行仿射变换纠正占据了部分的匹配耗时,故采用快速搜索算法在节省影像匹配耗时上具有可观的效益。
3.3 相机安置角误差检校试验分析 3.2.1 虚拟地面控制点坐标精度验证首先分析本文提出的虚拟地面控制点计算模型的正确性。由于试验中自动匹配获得的虚拟控制点一般位于平坦处,很难从点云中量取同名点作为参考值评价虚拟控制点的坐标精度,故采取人工量测的方式在基准片上均匀量测了18个4°及以上重叠的航带间加密点(主要为房角点)作为用于检查的虚拟控制点。对于每个检查点P,在点云中量测其坐标(XP,YP ,ZP),分别将该检查点对应的每一像点pi(i =0,1,2,…,m; m≥3)投影到ZP高程面上获取投影的平面坐标(XPi,YPi),并分别统计按式(3)计算的点P在单航带内投影点平面坐标加权均值以及其全部投影点平面坐标加权均值相对于点云中量测坐标的残差,统计结果如表 2所示,其中dX、dY、dXY分别表示X坐标残差、Y坐标残差以及平面整体残差。
| m | ||||||
| 残差项 | 单航带投影点平面坐标加权均值的精度 | 所有投影点平面坐标加权均值的精度 | ||||
| dX | dY | dXY | dX | dY | dXY | |
| 残差中误差 | 1.8693 | 0.4218 | 1.9163 | 0.3945 | 0.3014 | 0.4965 |
| 残差平均值 | 0.3673 | 0.2995 | 1.8962 | -0.0266 | 0.2158 | 0.4490 |
| 残差最大值 | -2.4376 | 0.8010 | 2.4877 | -0.7450 | 0.7083 | 1.0280 |
从表 2可见,所有投影点平面坐标加权均值的精度相比单航带投影点平面坐标加权均值的精度有明显提高。可见由于航带间飞行方向相反,在计算虚拟地面控制点的物方平面坐标时,可以在一定程度上抵消相机安置角误差的不利影响,获得较为准确平面坐标值。另由于虚拟地面控制点高程值从精度较高的点云获取(点云高程精度约0.2m),故虚拟地面控制点坐标平面精度和高程精度均较理想,此试验验证了本文设计的虚拟地面控制点计算模型的合理性。
3.2.2 相机安置角误差检校前后点云与影像套合情况分析在相机安置角误差检校过程中,对基准片影像进行匹配时,2级金字塔影像(1级金字塔影像即原始影像)相关窗口大小为19像素×19像素,2级金字塔影像搜索范围大小(不包括相关窗口的大小)为59像素×59像素(相当于原始影像上177像素×177像素,根据初始外方位元素的精度人工设定这一搜索范围),原始影像上相关窗口大小为11像素×11像素,原始影像上搜索范围大小为11像素×11像素,2级金字塔影像匹配相关系数阈值T2为0.70,原始影像匹配相关系数阈值T2为0.85。匹配获得443个加密点,初步剔除粗差后共有439个加密点,包含有3378个像点,其中4°及以上重叠航带间加密点342个。
为分析相机安置角误差检校前后的影像外方位元素精度,在测区内选择了多张航空影像,在其覆盖范围内的LiDAR点云中人工截取若干建筑物屋顶点,分别采用相机安置角误差检校前后的影像外方位元素将建筑物屋顶点反投影到相应影像上进行对比。因篇幅所限,图 5展示了测区中两幅影像(与基准片距离很远且不在同一航带上)上部分投影效果。从图 5可见,相机安置角误差检校后,屋顶点与影像套合效果得到明显改善,证实了本文相机安置角误差检校的有效性。

|
| 图 5 部分影像上建筑物屋顶点云投影结果(其中每组图片左右分别为相机安置角误差检校前后的投影结果) Fig. 5 The fitness of roof points to images (for each group,the left is the result before calibration and the right is the result after calibration) |
试验中选择了一些影像上的若干特征点,分析在相机安置角误差检校前后其预测同名点位与真实点位的接近程度。因篇幅限制,此处仅展示图 6中所示的一组预测结果,其中图 6(a)、图 6(b)分别为相机安置角误差改正前后特征点在同一重叠影像上的预测点位,图中的影像块进行过旋转和尺度纠正,图中图片所在的影像与参考影像的飞行方向相差大约180°,真实同名点位用白色圆圈标于图 6(a)中。试验中对所有预测点位进行分析后发现,相机安置角误差改正后,预测同名点位均非常接近真实位置,证实了相机安置角误差补偿的有效性。

|
| 图 6 某特征点在重叠影像上的预测点位 Fig. 6 The predicted conjugate point in correspond image |
在相机安置角误差改正后,通过搜索窗口大小自适应计算,确定2级金字塔影像(1级金字塔影像即原始影像)最大搜索范围大小为18×18(相当于原始影像上54像素×54像素)。搜索窗口与最初的设定值相比,减小了123像素×123像素,有效地缩小了搜索范围。2级金字塔影像相关窗口大小设定为15像素×15像素,原始影像上相关窗口大小为11像素×11像素,原始影像上搜索范围大小为11像素×11像素,2级金字塔影像匹配相关系数阈值为0.70,原始影像匹配相关系数阈值为0.85。为节省连接点匹配时间,匹配时将各影像划分成9×7个格网,每个格网选择一个特征点参与匹配。
表 3为测区影像匹配获得的各重叠度的加密点及其个数统计情况,总共获得加密点2201个,同名点13511对。其中6°及以上重叠加密点1036个,占总加密点数的47%,最高匹配出19°重叠的加密点。
| 重叠度 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12—19 | 总点数 |
| 加密点数 | 403 | 322 | 248 | 192 | 166 | 157 | 152 | 132 | 98 | 100 | 231 | 2201 |
图 7所示为某一特征点的匹配结果。从匹配结果可见,本文算法可以成功匹配出大旋角(90°或180°)、较大尺度差异的影像间同名点。

|
| 图 7 测区某一特征点部分匹配结果 Fig. 7 Matched conjugate points in four images |
为验证本文匹配算法的有效性,与不进行安置角误差检校、不采用相关系数快速匹配的传统的物方约束影像匹配进行了对比试验,试验结果如表 4所示。从表 4可见,传统算法匹配的加密点和对应像点数分别为2367和14780个,本文算法匹配获得的加密点和像点数分别为2201和13511个,其原因在于本文自适应地缩小了匹配搜索范围,减少了因搜索范围过大导致的误匹配像点的数目;对加密点进行光束法自由网平差后,本文算法的像点残差中误差为0. 00233mm,约为1/3像素大小,相对于传统算法的0.00245mm有所降低,其中传统算法和本文算法匹配后残差小于3倍对应的像点残差中误差大小的像点比例分别为87.6%和92.0%,证明本文算法提高了匹配正确率;传统算法和本文算法匹配总耗时分别为59min和39min,其中Harris特征点提取耗时均为14min,因本文算法进行安置角误差检校时需在基准影像上对所有特征点(625个)进行逐一匹配,故耗时6min。本文算法对相机安置角误差检校后自适应缩小了匹配搜索范围,且采用快速相关系数匹配,故在最终对所有影像进行连接点匹配时仅耗时19min,相比传统算法节省26min。考虑到安置角检校耗时固定且与测区影像数目和匹配连接点数目无关,当测区内影像数目越多、匹配连接点数目越多,本文算法所节省时间越可观。
| 匹配方法 | 匹配结果 | 匹配耗时/min | |||||||
| 加密点数 | 像点数 | 像点残差 中误差/mm | 残差小于3倍中 误差的像点比例 | Harris特征点 提取 | 安置角 检校 | 全部影像连接 点匹配 | 总耗时 | ||
| 传统算法 | 2367 | 14780 | 0.00245 | 87.6% | 14 | — | 45 | 59 | |
| 本文算法 | 2201 | 13511 | 0.00233 | 92.0% | 14 | 6 | 19 | 39 | |
针对机载LiDAR设备搭载数码相机获取的航空影像空三连接点匹配问题,本文提出一种LiDAR点云和POS辅助航空影像匹配方法。在基于物方约束的航空影像匹配算法基础上,提出了一种快速相关系数匹配算法;同时采用虚拟地面控制点进行相机安置角误差检校,提高影像外方位元素的精度,并在此基础上实现影像匹配搜索范围自适应确定;最后采用更新后的外方位元素和LiDAR点云数据辅助进行影像连接点匹配。
对快速相关系数匹配算法进行的大量试验结果表明,所提出的快速算法能够在几乎不影响匹配正确率的情况下节省约25%的匹配耗时。相机安置角误差检校的试验表明,本文设计的虚拟地面控制点具有较好的精度,相机安置角检校后点云与影像的套合效果以及匹配时同名点预测精度有了很大改善,匹配搜索范围自适应确定方法取得了良好的效果。采用本文设计的影像连接点匹配方法对62张影像进行了匹配试验,验证了该方法能匹配出大量6°及以上重叠的加密点,可以成功匹配出大旋角(90°或180°)、较大尺度差异影像间同名点,自由网平差精度达到约1/3像素,与传统算法相比提高了匹配精度、节省了大量匹配耗时。
由于本文所能获取的数据有限,无法进一步验证本文算法对于无序影像的连接点匹配效果,后续的研究工作可围绕此方面进行。此外,还可采用GPU并行匹配算法[22]进一步提高连接点匹配速度。
| [1] | BALTSAVIAS E P. A Comparison between Photogrammetry and Laser Scanning[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3): 83-94. |
| [2] | SHAN J, TOTH C K. Topographic Laser Ranging and Scanning: Principles and Processing[B]. Boca Raton: CRC Press, 2008: 445-477. |
| [3] | YASTIKLI N, TOTH C, GREJNER-BRZEZINSKA D A. In-situ Camera and Boresight Calibration with LiDAR Data[C]//Proceedings of the fifth International Symposium on Mobile Mapping Technology. Padua: ISPRS, 2007. |
| [4] | IP A, EI-SHEIMY N, MOSTAFA M. Performance Analysis of Integrated Sensor Orientation[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(1): 1-9. |
| [5] | ZHANG Yongjun, XIONG Xiaodong, SHEN Xiang. Automatic Registration of Urban Aerial Imagery with Airborne LiDAR Data[J]. Journal of Remote Sensing, 2012, 16(3): 579-595. (张永军, 熊小东, 沈翔. 城区机载LiDAR数据与航空影像的自动配准[J]. 遥感学报, 2012, 16(3): 579-595.) |
| [6] | SCHENK T. Towards Automatic Aerial Triangulation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1997, 52(3): 110-121. |
| [7] | KRUPNIK A, SCHENK T. Experiments with Matching in the Object Space for Aerotriangulation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1997, 52: 160-168. |
| [8] | TANG L, BRAUN J, DEBITSCH R. Automatic Aerotriangulation: Concept, Realization and Results[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1997, 52(3):122-131. |
| [9] | ZEBEDIN L, KLAUS A, GRUBER-GEYMAYER B, et al. Towards 3D Map Generation from Digital Aerial Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(6): 413-427. |
| [10] | WILKINSON B E, DEWITT B A, WATTS A C, et al. A New Approach for Pass-point Generation from Aerial Video Imagery[J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(12): 1415-1423. |
| [11] | BARAZZETTI L, SCAIONI M, REMONDINO F. Orientation and 3D Modelling from Markerless Terrestrial Images: Combining Accuracy with Automation[J]. The Photogram-metric Record, 2010, 25(132): 356-381. |
| [12] | ZHANG Y J, XIONG J X, HAO L J. Photogrammetric Processing of Low-altitude Images Acquired by Unpiloted Aerial Vehicles[J]. Photogrammetric Record, 2011, 26(134): 190-211. |
| [13] | LERMA J L, NAVARRO S, CABRELLES M, et al. Automatic Orientation and 3D Modelling from Markerless Rock Art Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 76: 64-75. |
| [14] | XIONG Xinghua, CHEN Ying, QIAN Zengbo. A Fast, Accruate and Robust Image Matching Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 40-45. (熊兴华, 陈鹰, 钱曾波. 一种快速、高精度和稳健的影像匹配算法[J]. 测绘学报, 2005, 34(1): 40-45.) |
| [15] | ZHAO Xian, CHEN Zhixue, LV Jingguo, et al. The Scale and Rotating Invariant Auto Stereo Matching[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 81-86. (赵西安, 陈志学, 吕京国, 等. 具有尺度与旋转不变性的立体影像自动匹配研究[J]. 测绘学报, 2012, 41(1): 81-86.) |
| [16] | JI Shunping, YUAN Xiuxiao. Automatic Matching of High Resolution Satellite Images Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 592-598. (季顺平, 袁修孝. 基于RFM的高分辨率卫星遥感影像自动匹配研究[J]. 测绘学报, 2010, 39(6): 592-598.) |
| [17] | ZHANG Guo, CHEN Tan, PAN Hongbo, et al. Patch-based Least Squares Image Matching Based on Rational Polynomial Coeffcients Model[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 592-597. (张过, 陈钽, 潘红播, 等. 基于有理多项式系数模型的物方面元最小二乘匹配[J]. 测绘学报, 2011, 40(5): 592-597.) |
| [18] | YUAN Xiuxiao, MING Yang. POS-supported Matching Method for Aerial Images between Neighboring Strips[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 156-161. (袁修孝, 明洋. POS 辅助航带间航摄影像的自动转点[J]. 测绘学报, 2010, 39(2): 156-161.) |
| [19] | ZHANG Yongjun, XIONG Jinxin, XIONG Xiaodong, et al. Main Error Source of Vertical Parallax and Compensation Regression Model of POS Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 604-609. (张永军, 熊金鑫, 熊小东, 等. POS数据的上下视差误差源检测及误差补偿回归模型[J]. 测绘学报, 2011, 40(5): 604-609.) |
| [20] | CHEN S Y, MA H C, ZHANG Y C, et al. Boresight Calibration of Airborne LiDAR System without Ground Control Points[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 85-89. |
| [21] | WALKER A S. Responses to Users: The Continuing Evolution of Commercial Digital Photogrammetry[J]. Photogrammetric Record, 1999, 16(93): 469-483. |
| [22] | XIAO Han, ZHANG Zuxun. Parallel Image Matching Algorithm Based on GPGPU[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 46-51. (肖汉, 张祖勋. 基于GPGPU 的并行影像匹配算法[J]. 测绘学报, 2010, 39(1): 46-51.) |