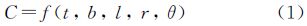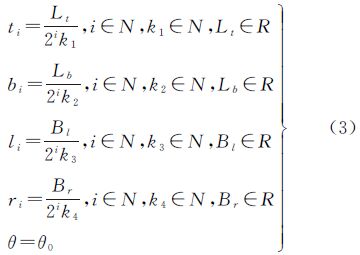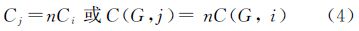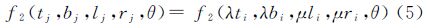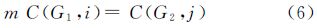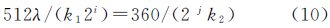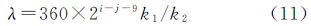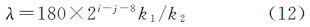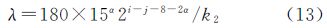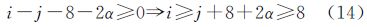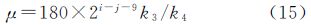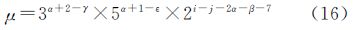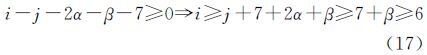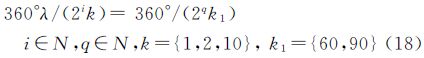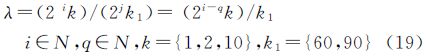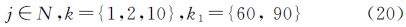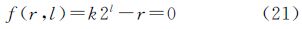2. 北京大学 航空航天信息工程研究所,北京100871;
3. 中煤科技集团公司,北京 100013
2. Institute for Aeronautics and Astronautics Information Engineering,Peking University,Beijing 100871,China;
3. China Coal Technologies Group Corp,Beijing 100013,China
在实际应用中,空间数据种类繁多、关系复杂,且不同行业有不同内容的专业数据,空间数据的生产、维护分散在不同的单位且采用的数据网格标准各异,造成了部门或系统之间、不同历史阶段之间数据产品规格不统一[1]。例如,卫星地面数据接收中心的原始遥感影像数据按照轨道景或轨道条带组织,而轨道景、轨道条带主要依据格网参考系GRS(Grid Reference System)和世界参考系WRS(Worldwide Reference System)所形成的固定参考网格并利用Path/Row对轨道景编码[2, 3];测绘部门的正射影像数据产品,高级数据产品(4级以上)按照地图图幅标准进行组织,低级数据产品按照轨道景数据组织;广泛使用的空间数据服务,如Worldwind、Google Earth、天地图等,均采用构建影像金字塔的方式进行数据组织。这种不同部门建立各自独立的遥感数据组织和索引方式,可很好地适应本部门内业务需要,但跨部门间数据应用时,不同的数据组织和记录方式给用户带来了很大的困难,不利于空间信息的检索、整合、共享与分发等。
为解决上述问题,本文提出基于GeoSOT (geographical coordinate subdividing grid with one dimension integer coding on 2n-tree)网格[4]的全球遥感影像数据剖分组织,为遥感数据高效应用奠定基础。
1 国内外研究现状近年来,国内外学者对全球离散网格[5, 6]有很深入的研究,取得了很多成果,具体归纳为如下几类。第1类是基于柏拉图立体的正多面体(4面体、立方体、8面体、12面体和20面体)网格[7, 8],如O-QTM(octahedral-quaternary triangular mesh)[9, 10]、SQT(sphere quadtree)[11, 12]和STQIE(spherical triangle quadtree based on Icosahedron and ERLRP)[13, 14, 15];第2类是基于正六边形的全球离散网格[8, 16, 17, 18];第3类是基于Voronoi图的自适应全球离散网格[19, 20, 21];第4类是基于地理坐标划分的全球离散网格,如多级网格[22]、Worldwind网格[2]、Google Earth和Google Maps网格[2]、Bing Maps网格[23]、天地图网格[23]和我国测绘数据网格[24]等。
这些全球离散网格具有自身的特点。第1类全球离散网格可使得各网格单元在全球范围内的形状相似、各向同性,但各单元为球面三角形,从多面体到球体的映射关系比较复杂[25];第2类全球离散网格最紧凑、具有唯一的邻域,可用6个离散的速度向量描述连续的各向同性的流体[26],但上下层之间的网格单元不像三角形网格那样具有层次性和对称性,而是存在一定角度的旋转;第3类网格可针对空间数据的分布情况动态生成网格,适合组织空间点数据,但该网格单元不规则、无层次性,无法与比例尺和分辨率对应,且动态生成Voronoi图计算复杂,结构繁琐[27];第4类全球离散网格多是按经纬度网格进行划分,坐标转换方便,但高纬度地区存在一定的变形[27]。针对遥感影像数据的矩形点阵结构的特点,基于三角形、六边形和Voronoi图等的网格,由于网格单元与影像数据块单元不一致,在组织管理遥感影像数据,需大量复杂数据转换工作,使得这3类网格仅用于理论研究和少数应用[28, 29],组织管理遥感影像数据均存在一定的局限性。基于经纬度坐标的全球离散网格单元与影像数据点阵相似以及坐标转换简单等优点,被Google Earth、Worldwind、天地图等广泛地应用。因此,本文主要对经纬度坐标全球离散网格讨论。同时,我国遥感影像数据产品多按地图图幅组织,Worldwind、Google Earth、Bing Maps和天地图等网格单元大小并不是整度、整分和整秒划分,不能无缝地拼接为地图图幅(具体见后面理论证明),对跨部门之间遥感数据组织网格的兼容性和历史数据继承等问题考虑较少,在制作遥感影像数据产品还需数据拼接、裁剪等数据处理。
在此背景下,以北京大学程承旗教授为首的研究团队提出了GeoSOT剖分网格理论,期望利用GeoSOT网格独特的性质,解决跨部门之间、部门内各业务阶段遥感影像数据组织基准不统一的问题。
2 GeoSOT网格及特点分析 2.1 GeoSOT网格与编码为了使得全球网格单元(剖分面片)大小为二进制整型、便于与地图图幅网格兼容,GeoSOT网格通过地球表面经纬度范围空间经过3次扩展后再对其进行严格的递归四叉剖分。具体GeoSOT网格划分方法如下:首先将地球通过简单投影变换到平面,将180°×360°地球表面空间扩展为512°×512°,并将该空间作为第0级剖分面片(cell),且面片中心与赤道和本初子午线的交点重合(见图 1(a)和图 1(b))。在此基础上,对第0级剖分面片进行递归四叉剖分,直到1°剖分面片。为了进行整分剖分,对1°剖分面片先进行扩展,即从60′扩展为64′(见图 1(e)),再对扩展的剖分面片递归四叉剖分,直到1′大小的剖分面片。对于1′网格面片,同样先将其扩展到64″(见图 1(f)),然后递归四叉剖分直到32级(1/2048)″。这样,GeoSOT网格产生整度、整分、整秒和秒下级等多级剖分网格(见图 1(c))。这样,经纬度坐标空间经过3次扩展后,整个地球表面经纬度空间在经线方向和纬线方向可严格的整型二分,由此将整个地球分割为大到全球、小到厘米级的整度、整分和整秒的层次网格。

|
| 图 1 GeoSOT网格多级剖分与3次扩展示意图 Fig. 1 Multi-level subdivision and three extension of GeoSOT |
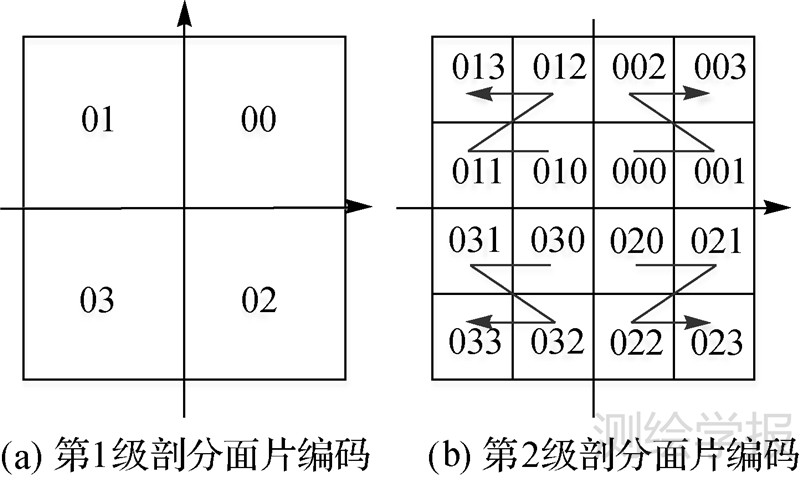
针对GeoSOT网格剖分方案,采用64位编码对各级剖分面片进行标识。其中,第0级剖分面片标识为0,第1级剖分面片编码分别为00、01、02和03(见图 2(a)),并从第2级开始,下一级剖分面片的编码在上一级剖分面片编码后追加0、1、2和3。具体编码规则是,距赤道和本初子午线的交点最近的剖分面片为0,最远的为3,然后按照先沿纬线方向再沿经线方向对其他两个剖分面片分别为1和2(见图 2(b))。
|
| 图 2 GeoSOT网格单元的编码 Fig. 2 GeoSOT cells’ codes |
由于GeoSOT网格是基于经纬度整度、整分、整秒的递归四叉剖分,与Google Earth、Worldwind、Bing Maps和天地图等格比较,GeoSOT网格与测绘数据地图图幅具有很好的同构性,证明如下。
为了方便后面的证明,首先介绍有关网格同构的几个概念,且讨论的全球经纬度网格是将球面网格投影到平面后的全球经纬度网格。
2.2.1 基本概念定义1:在全球经纬度网格G中,若映射f适合
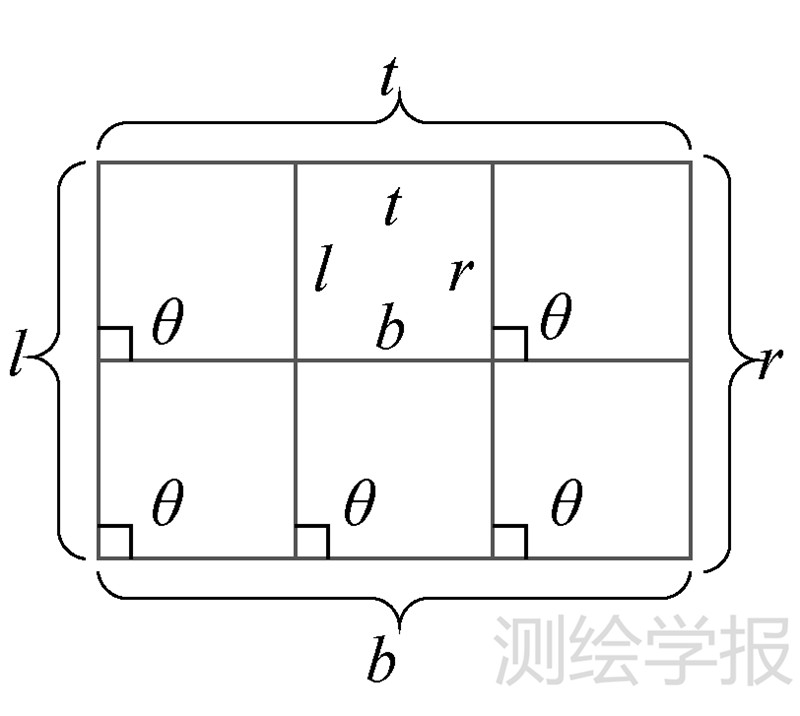
式中,t、b、l、r代表网格单元的四边长度;θ代表任意两邻边的夹角,则称C为网格G的单元。其中,t、 b、 l、 r、 θ单位为度(°)。
第i层全球经纬度网格G的单元C,记作C(G,i)或Ci,表示如下
在全球经纬度网格G单元Ci=f(ti,bi,li,ri,θ)中,参数取值如下
式中,Lt、Lb、Bl、Br为整个地球或者第1层单元格的经度和纬度长度,单位为度(°)。当Lt、Lb、Bl、Br、k1、k2、k3、k4和θ0取不同值时,即可表示不同全球经纬度网格。
根据定义1,NASA Worldwind、Google Earth、Bing Maps、天地图、我国测绘数据规格网格和GeoSOT等网格单元Ci=f(ti ,bi ,li ,ri ,θ),其参数取值如表 1所示。
| 数据网格 | ti | bi | li | ri | θ |
| Worldwind | ti=bi =360/(10×2i),i∈N,Lt=Lb=360, k1= k2=10 | li=ri =180/(5×2i),i∈N,Bl=Br=180,k3= k4=5 | 90 | ||
| Google Earth | ti=bi =360/2i,i∈N,Lt=Lb=360, k1= k2=1 | li=ri =180/2i,i∈N,Bl=Br=180,k3= k4=1 | 90 | ||
| Bing Maps | ti=bi =360/(2×2i),i∈N,Lt=Lb=360, k1= k2=2 | li=ri =180/(2×2i),i∈N,Bl=Br=180,k3= k4=2 | 90 | ||
| 天地图 | ti=bi =360/(2×2i),i∈N,Lt=Lb=360, k1= k2=2 | li=ri =180/2i,i∈N,Bl=Br=180,k3= k4=1 | 90 | ||
| 中国地图图幅 | 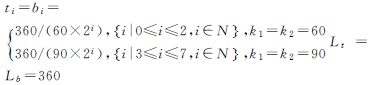 |  | 90 | ||
| GeoSOT网格 | 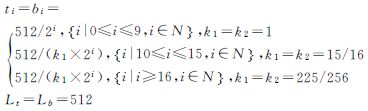 | 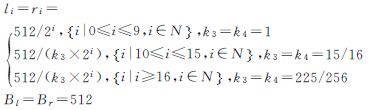 | 90 | ||
定义2:对于全球经纬度网格G1和G2,C(G1,i)= f1(ti,bi,li,ri,θ1)和C(G2,j)= f2(tj,bj,lj,rj,θ2)(i,j∈N)分别是G1第i层和G2第j层的网格单元。若n(n∈N)个相邻的C(G1,i)覆盖的空间范围与C(G2,j)覆盖的空间范围相同,则称G1可聚合成G2。特别的,G1与G2可以是同一个全球经纬度网格。
若tj=λti,bj=λbi,lj=μli,rj=μri,θ1=θ2=θ且n=λμ(1≤λ≤n,1≤μ≤n,λ∈N,μ∈N,n∈N)时,称为长度聚合(如图 3),表示为
或
|
| 图 3 长度聚合示意图 Fig. 3 Length of aggregation |
定义3:对于全球经纬度网格G1和G2,C(G1,i)(i∈N)和C(G2 ,j)(j∈N)分别是G1和G2的单元。若有限个C(G1,i)聚合而成的空间范围与C(G2,j)的覆盖空间范围不相等,但形状相同,则称G1弱聚合成G2。
定义4:对于全球经纬度网格G1、G2和G3,若G1可聚合成G2,而G1可弱聚合成G3,则称G2与G3弱同构。
因此,对于全球经纬度网格G1和G2,若G1和G2的θ相等,G1和G2必是弱同构。其证明见附录。
定义5:对于全球经纬度网格G1、G2和G3,若G1可聚合成G2,同时G1也可聚合成G3,则称G2与G3同构。特别的,全球经纬度网格G与其本身同构。
2.2.2 GeoSOT网格与其他数据网格的同构性分析根据定义4,若要证明GeoSOT网格与其他全球经纬度网格同构,只需证明GeoSOT网格可聚合成其他全球经纬度网格即可,具体证明如下。
证明:对GeoSOT网格G1与其他全球经纬度网格G2,假设C(G1,i)(i∈N)和C(G2,j)(j∈N)分别是G1第i层和G2第j层的网格单元。要证明G1与G2同构,也就是要证明存在正整数m(m∈N),使得G1中m个单元C(G1,i)可聚合成G2单元C(G2,j),即
根据定义2,证明式(6)成立等价于证明存在λ∈N,μ∈N,使得下面3个等式成立
而对式(7),将表 1中的ti代入得
因为k1∈{1,15/16,225/256},k2∈{1,2,10,60,90},因此式(11)变换为
在式(12)中,180/k2∈N,k1可以表示为k1=15α/22α,α∈{0,1,2},并代入式(12)得
在式(13)中,180/k2∈{2,3},15α≥1,只要使得2i-j-8-β≥1即可,即
也就是,当GeoSOT网格层级i≥8时,总可使得式(13)中λ为正整数。
同理,将表 1中GeoSOT网格li和其他经纬度网格的lj代入式(8)得
而k3∈{1,15/16,225/256},k4∈{1,2,5,45,135/2},则令k3=15α/22α,α∈{0,1,2},k4=2β×3γ×5ε,β∈{-1,0,1},γ∈{0,2,3},ε∈{0,1},则式(15)变换为
要使得μ为正整数,只要式(16)右边为正整数即可。而5α+1-ε≥1,且当α和γ取特定的值时3α+2-γ≥1,所以只要使得2i-j-2α-β-7≥1,即
也就是,当GeoSOT网格G1层级i≥6时,总可使得式(16)中μ为正整数。
因此,根据式(14)和式(17),对于表 1中的其他全球经纬度网格G2,只要GeoSOT网格G1层级i≥7时,总存在正整数m=λμ使得式(6)成立,即证GeoSOT网格与其他全球经纬度网格同构。
而Worldwind、Google Earth、Bing Maps、天地图等网格与测绘数据规格网格具有弱同构性,可采用反证法进行证明。
证明:假设Worldwind、Google Earth、Bing Maps、天地图等网格与测绘数据规格网格同构性。
根据定义2,只要存在λ整数,使得式(18)成立,即证明Worldwind、Google Earth、Bing Maps、天地图等网格与测绘数据规格网格同构性
也就是
令j=i-q,则式(19)变换为
由于2j始终为偶数,k1={60,90}为2、3、5等素数的合数,因此要使得λ为整数,则式(20)中左边k必须为3的倍数。而Google Earth、Worldwind、Bing Maps、天地图等网格模型中k取值为{1,2,10},不是3的倍数,所以式(20)中左边结果为非整数,即λ为小数,与假设λ为整数矛盾,所以假设为错误。而Worldwind、Google Earth等网格与测绘数据规格网格的夹角θ相等,因此Worldwind、Google Earth等网格与测绘数据规格网格弱同构性。
3 基于GeoSOT网格的遥感数据组织鉴于GeoSOT网格的多尺度性以及与我国测绘数据规格网格同构的特点,在不改变现有数据组织的前提下,本文提出通过逻辑剖分,建立以GeoSOT网格剖分面片为遥感影像景划分单元,实现基于空间区域的遥感数据“全球一张网”组织,提高多源多类型遥感数据使用效率。
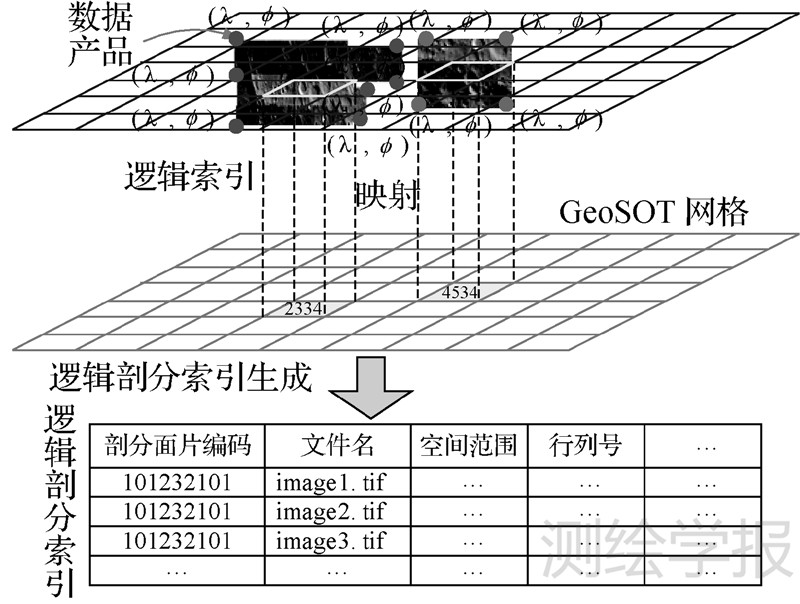
3.1 遥感数据“全球一张网”数据组织我国经过几十年的发展积累了大量的遥感数据,若这些数据都按GeoSOT剖分面片进行物理分景处理,必是一个耗时耗力的巨大工程,且可能对目前遥感数据生产流程带来影响。因此,本文提出的基于GeoSOT遥感数据组织思路是,在不改变目前遥感数据组织模式的前提下,首先根据遥感数据的地理坐标范围,确定该数据的最小外包面片MBC(minimum bounding cell),并将MBC面片编码作为整幅遥感数据的剖分标识,写入剖分索引表中,然后根据遥感数据的空间分辨率确定所在GeoSOT层,并通过GeoSOT剖分面片单元4个角点地理坐标与遥感数据的地理坐标对应,对遥感数据按GeoSOT网格剖分面片空间范围进行“虚拟划分”,即逻辑剖分,将遥感影像数据覆盖剖分面片的编码与剖分面片4个角点对应遥感影像数据像素行列号等信息,写入与遥感影像文件名相同的剖分索引文件中,由此建立基于GeoSOT剖分面片编码的遥感数据块剖分索引,从而实现遥感数据按空间区域数据组织。由于GeoSOT网格剖分面片覆盖全球且大小固定,与剖分面片关联的遥感数据也虚拟覆盖全球且遥感数据大小规格一定,形成遥感数据虚拟“全球一张网”的数据组织体系,如图 4所示。
|
| 图 4 遥感数据建立逻辑剖分的流程图 Fig. 4 Logical subdivision of remote sensing data |
此方案中,遥感数据与GeoSOT网格层级l的对应关系采用的如下公式确定
式中,r为遥感数据分辨率,单位为°/像素;l为GeoSOT网格层级;k为常数,一般取2-n,n∈N。
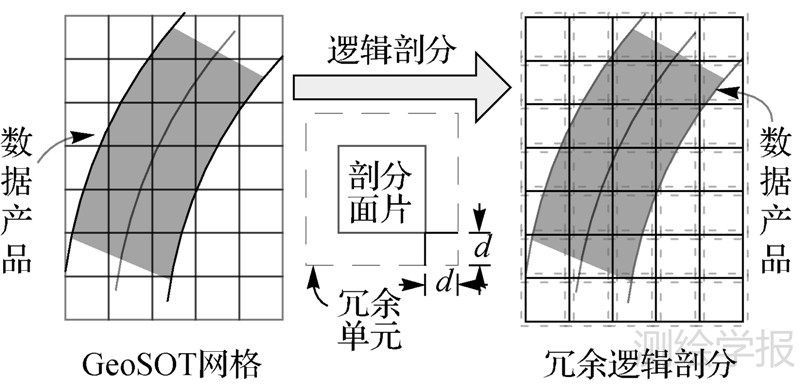
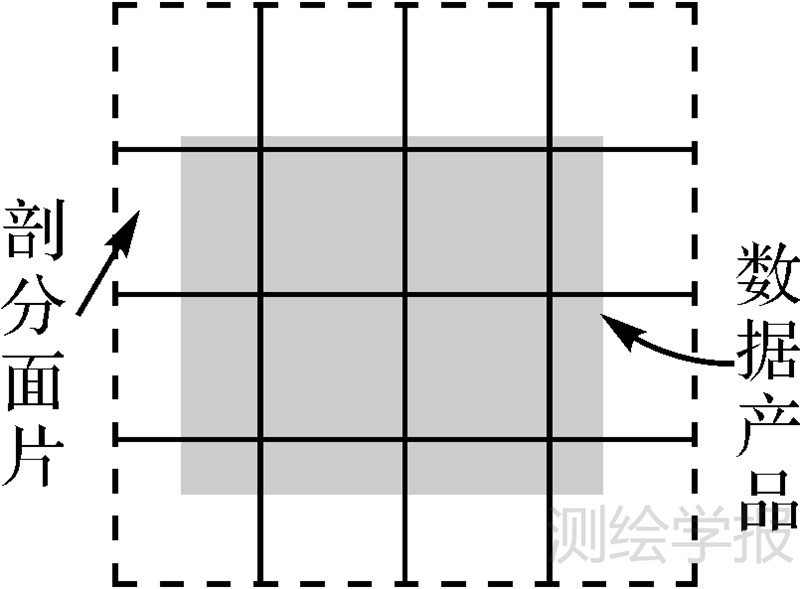
同时,由于各级剖分面片空间范围固定,而不同等级的影像数据产品几何精度不同,导致基于剖分面片“分割”的遥感影像数据会产生一些问题。例如,对地理精度误差较大的低级别(3级以下)的遥感影像,由于其存在较大的几何精度误差,导致本应该与剖分面片A关联的数据块,分割后可能与A相邻的剖分面片B关联。为了避免出现上述现象,在对不同地理精度误差的遥感影像数据逻辑剖分时,分别采用冗余逻辑剖分和精确逻辑剖分。对地理精度误差较大的低级别(3级以下)遥感影像数据逻辑剖分时,将剖分面片空间范围向周围扩展遥感影像地理误差的宽度,并按扩展后的剖分面片“分割”遥感影像,即为冗余逻辑剖分,从而使得地球表面与剖分面片地理范围对应区域的遥感影像数据始终在关联的剖分面片内。图 5为地理精度误差为d的遥感数据产品冗余逻辑剖分示意图,实线单元格为GeoSOT剖分面片,虚线网格为根据精度误差d扩展后的冗余剖分面片,冗余逻辑剖分即按虚线对影像数据进行“分割”。而对于地理精度误差较小的高级(4级以上)影像数据产品,直接根据GeoSOT剖分面片的空间范围进行逻辑剖分,建立遥感数据逻辑剖分索引,即为精确逻辑剖分,如图 6所示。
|
| 图 5 低级影像数据产品的冗余逻辑剖分示意图 Fig. 5 Redundant logical subdivision of lower-level remote sensing data products |
|
| 图 6 高级影像数据产品的精确逻辑剖分示意图 Fig. 6 Precise logical subdivision of advanced remote sensing data products |
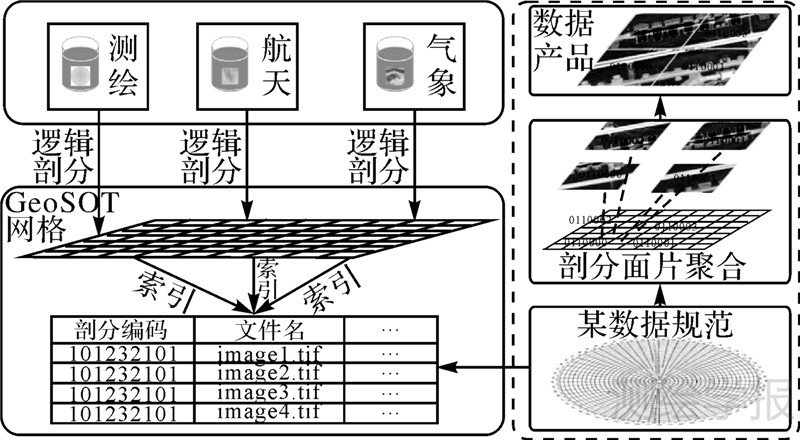
基于GeoSOT遥感数据“全球一张网”的数据组织,使得遥感数据具有共同的数据组织基础,可避免不同部门、不同型号卫星遥感数据采用的数据组织网格不一致问题。同时使得大区域的遥感数据可直接聚合得到,即当利用遥感数据制作某规格数据产品时,根据规格数据产品的空间范围信息,例如地图图幅范围,计算出规格产品范围覆盖的剖分面片,并根据剖分面片编码提取相关的遥感数据。最后,根据GeoSOT网格与其他规格数据网格同构性,通过剖分面片聚合的方式即可快速生成规格数据产品(如图 7),可有效减少参与计算的遥感数据数据量,从而提高遥感数据整合效率。
|
| 图 7 基于GeoSOT网格剖分面片聚合的数据产品生产过程 Fig. 7 Process of products aggregated by GeoSOT cells |
根据GeoSOT网格及编码模型,在Worldwind开源代码的基础上,利用Microsoft Visual studio 2008 C#作为开发平台,Microsoft Office Access2007作为后端数据库系统,在CPU主频为2.4 GHz、内存为2 GB、硬盘转速为7200 rpm的PC机上进行了遥感数据GeoSOT组织与数据整合的试验验证。试验数据为局部地区某卫星1A、2B和3B级约32 GB遥感影像数据,分辨率分别为2 m、5 m和10 m,其格式为TIF文件。当式(21)中k取值为1/512,则上述分辨率的遥感影像分别对应GeoSOT网格第15层、第14层和第13层。对地理精度相对较低的1A级影像数据采用冗余逻辑剖分,而对地理精度相对较高的2B级和3B级影像数据采用精确逻辑剖分处理。3种不同级别影像建立逻辑剖分索引的耗时如表 2。
| 数据级别 | 数据量/GB | 剖分处理耗时/s | 耗时率/(s/GB) |
| 1A级 | 7.2 | 6.77 | 0.94 |
| 2B级 | 7.03 | 5.94 | 0.845 |
| 3B级 | 17.4 | 17.8 | 1.024 |
在影像逻辑剖分组织的基础上,利用GeoSOT网格与测绘地形图图幅之间的同构关系,通过剖分面片编码对单个剖分面片对应的影像数据以及不同区域、比例尺地图图幅的影像数据进行了数据检索和提取试验,其试验结果如表 3所示。
| 空间范围 | 级数 | 面片数/个 | 平均整合时间/ms |
| 3°×2° | 13 | 3072 | 997 |
| 15′×15′ | 15 | 450 | 871 |
| 1°×1° | 13 | 512 | 643 |
从表 3可看出,由于遥感数据建立了基于GeoSOT网格的逻辑剖分索引,在对剖分面片或规格产品范围对应的遥感数据进行数据整合具有较高的效率。
需要说明的是,本测试系统主要是验证遥感数据按GeoSOT网格进行逻辑剖分组织的效率和基于剖分面片聚合的数据整合的效率,以此说明基于GeoSOT的遥感数据组织的可行性和遥感数据应用的高效性。
5 结 论本文对目前常用的全球经纬度网格和GeoSOT网格进行了分析,理论证明GeoSOT网格较Google Earth、Worldwind、BingMaps和天地图等网格,与现有的测绘数据规格网格具有更好的同构性。鉴于GeoSOT网格的多尺度性和对我国测绘数据规格网格同构性特点,在不改变现有遥感数据组织的前提下,提出了通过基于GeoSOT网格的逻辑剖分方法,实现基于空间区域的遥感数据“全球一张网”组织。同时,本文还提出了基于剖分面片聚合的规格数据产品生成方法,可有效减少参与计算的遥感数据量,从而提高遥感数据整合效率。最后,通过试验验证,通过对现有的遥感数据建立逻辑剖分索引,实施代价不大,且基于GeoSOT的统一数据组织有助于规格数据产品的数据整合。
附 录:全球经纬度网格G1和G2弱同构证明。
证明:对于全球经纬度网格G1和G2,C(G1,i)= f1(ti,bi,li,ri,θ1)和C(G2,j)=f2(tj,bj,lj,rj,θ2)(i,j∈N)分别是G1第i层和G2第j层的网格单元,且tj>ti>0、lj>li>0、θ1=θ2。
由于θ1=θ2,则C(G1,i)和C(G2,j)可以进行长度聚合。而要证明G1和G2弱同构,则只要证明存在正整数n1和n2,使得n1ti > tj,n2li>lj即可。
取N1=[tj/ti]+1,N2=[lj/li]+1,对于任意的正整数n1和n2,当n1> N1,n2> N2时,n1ti > N1ti > titj/ti= tj,n2li > N2li >lilj/li= lj同时成立。
即证,G1与G2是弱同构。
| [1] | SHAO Zhenfeng, LI Deren. Study on Spatial Information Multi-grid under Grid Computing Environment[J]. Geomatics World, 2005, 3(2): 31-35. (邵振峰,李德仁. 基于网格计算环境下的空间信息多级格网研究[J]. 地理信息世界, 2005, 3(2): 31-35.) |
| [2] | SONG Shuhua. Research on a Universal Scene Model of Remote Sensing Data and Its Applications[D]. Beijing: Peking University, 2011. (宋树华. 遥感数据标准分景框架及其应用模型研究[D]. 北京: 北京大学, 2011.) |
| [3] | LI Jinping, LI Yonggang, LIU Xiufang. Research on the Estimate Method of Landsat WRS Grid Coordinate Position[J]. Science of Surveying and Mapping, 2006, 31(3): 52-53. (李锦萍, 李永刚, 刘秀芳. Landsat卫星WRS格网坐标位置估算方法的研究[J]. 测绘科学, 2006, 31(3): 52-53. ) |
| [4] | CHENG Chengqi, REN Fuhu, PU Guoliang, et al. An Introduce to Spatial Informaiton Subdivision Organization[M]. Beijing: Science Press, 2012. (程承旗, 任伏虎, 濮国梁, 等. 空间信息剖分组织导论[M]. 北京: 科学出版社, 2012.) |
| [5] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. |
| [6] | GOODCHILD M. Discrete Global Grids for Digital Earth[C]// Proceedings of International Conference on Discrete Global Grids. Santa Barbara: [s.n.], 2000. |
| [7] | WHITE D. Global Grids from Recursive Diamond Subdivisions of the Surface of an Octahedron or Icosahedrons[J]. Environmental Monitoring and Assessment, 2000, 64(1): 93-103. |
| [8] | GOLAY J E. Hexagonal Parallel Pattern Transformations[J]. IEEE Transactions on Computers, 1969, 18(8): 733-739. |
| [9] | DUTTON G. A Hierarchical Coordinate System for Geoprocessing and Cartography[M]. Berlin: Springer-Verlag, 1999. |
| [10] | DUTTON G. Encoding and Handling Geospatial Data with Hierarchical Triangular Meshes[C]//Proceedings of 7th International Symposium on Spatial Data Handling. Amsterdam: Taylors and Francis, 1996. |
| [11] | FEKETE G. Rendering and Managing Spherical Data with Sphere Quadtrees[C]// Proceedings on Visualization’90. New York: ACM, 1990. |
| [12] | FEKETE G, TREINISH L. Sphere Quadtrees: A New Data Structure to Support the Visualization of Spherically Distributed Data[C]//Extracting Meaning from Complex Data: Processing, Display, Interaction. Santa Clara:SPIE,1990, 1259: 242-253. |
| [13] | YUAN Wen, CHENG Chengqi, MA Ainai, et al.L Curve for Spherical Triangle Region Quantrees[J]. Science China: Technological Science,2004,47(3): 265-270. |
| [14] | YUAN Wen. STQIE Model for GeoGrid and the Prototype System[D]. Beijing: Peking University, 2004. (袁文. 地理格网STQIE 模型及原型系统[D]. 北京: 北京大学, 2004.) |
| [15] | YUAN Wen, MA Ainai, GUAN Xiaojing. A New Projection for Spherical Triangle: Equal Angle Ratio Projection(EARP)[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 78-84. (袁文,马蔼乃, 管晓静. 一种新的球面三角投影:等角比投影(EARP)[J]. 测绘学报, 2005, 34(1): 78-84.) |
| [16] | TONG Xiaochong, BEN Jin, QIN Zhiyuan, et al. The Subdivision of Partial Grid Based on Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 506-513. (童晓冲, 贲进, 秦志远, 等. 基于全球离散网格框架的局部网格划分[J]. 测绘学报, 2009, 38(6): 506-513.) |
| [17] | BEN Jin, TONG Xiaochong, ZHANG Yongsheng, et al. Research on Generating Algorithm and Software Model of Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 187-191. (贲进, 童晓冲, 张永生, 等. 球面等积网格系统生成算法与软件模型研究[J]. 测绘学报, 2007, 36(2): 187-191.) |
| [18] | ZHANG Yongsheng, BEN Jin, TONG Xiaochong, et al. Geospatial Information Processing Method Based on Spherical Hexagon Grid System[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(2): 110-114. (张永生, 贲进, 童晓冲, 等. 基于球面六边形网格系统的空间信息处理方法[J]. 测绘科学技术学报, 2006, 23(2): 110-114. ) |
| [19] | XU Yinfeng, YANG Boting. Popularization of Voronoi Diagram[J]. Chinese Journal of Engineering & Mathematics, 1995, 12(2): 93-96. (徐寅峰, 杨波艇. Voronoi图在球面上的推广[J].工程数学学报, 1995, 12(2): 93-96.) |
| [20] | ZHAO X S, CHEN J, LI Z L. A Mix Global Data Structure Based on QTM and Voronoi[C]//Proceedings of XXth ISPRS Congress. Istanbul: ISPRS, 2004: 791-796. |
| [21] | ZHAO Xuesheng, CHEN Jun, WANG Jinzhuang. QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 157-163. (赵学胜, 陈军, 王金庄. 基于O-QTM的球面Voronoi图的生成算法[J]. 测绘学报, 2002, 31(2): 157-163.) |
| [22] | LI Deren, ZHU Xinyan, GONG Jianya. From Digital Map to Spatial Information Multi-grid: A Thought of Spatial Information Multi-grid Theory[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 642-650. (李德仁, 朱欣焰, 龚健雅. 从数字地图到空间信息网格: 空间信息多级网格理论思考[J]. 武汉大学学报: 信息科学版,2003, 28(6): 642-650.) |
| [23] | LV X F, CHENG C Q, GONG J Y, et al. Review of Data Storage and Management Technologies for Massive Remote Sensing Data[J]. Science China: Technological Science, 2011, 54(12): 3220-3232. |
| [24] | Institute on Standardiztion of National Adminstration of Suveying, Mapping and Geoinformation. GB/T 13989-2012 Subdivision and Numbering for the National Primary Scale Topographic Maps[S]. Beijing: China Zhijian Publishing House, 2012. (GB/T13989-92,(国家测绘地理信息局测绘标准化研究所. GB/T13989-2012国家基本比例尺地形图分幅和编号[S].北京: 中国质检出版社, 2012.) |
| [25] | LI Deren, XIAO Zhifeng, ZHU Xinyan,et al.Research on Grid Division and Encoding of Spatial Information Multi-grids[J].Acta Geodaetica et Cartographica sinica, 2006, 35(1): 52-56. (李德仁, 肖志峰, 朱欣焰, 等. 空间信息多级网格的划分方法及编码研究[J]. 测绘学报, 2006, 35(1): 52-56.) |
| [26] | FRISCH U, HASSLACHER B, POMEAU Y. Lattice-gas Automata for the Navier-Stokes Equations[J]. Physical Review Letters, 1986, 56(3): 1505-1508. |
| [27] | SONG Shuhua, CHENG Chengqi, GUAN Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-Information Science, 2008, 24(4): 11-15. (宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4): 11-15.) |
| [28] | BARTHOLDI J, GOLDSMAN P. Continuous Indexing of Hierarchical Subdivisions of the Globe[J]. International Journal of Geographical Information Science, 2001, 15(6): 489-522. |
| [29] | SAHR K, WHITE D, KIMMERLING A. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. |