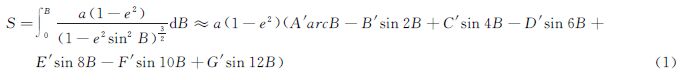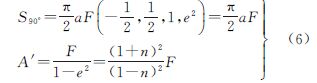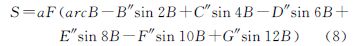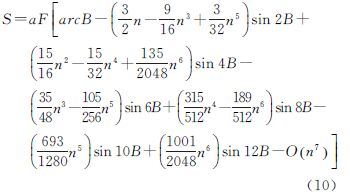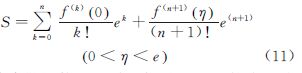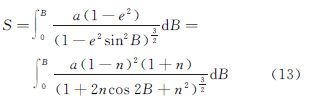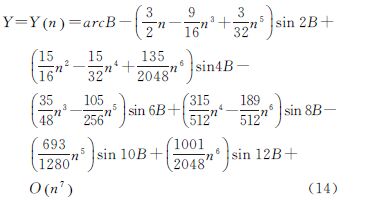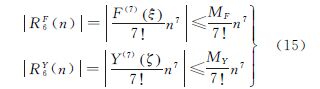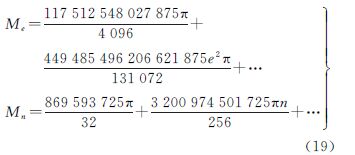2. 江西省数字国土重点实验室，江西 抚州 344000
2. Jiangxi Province Key Lab for Digital Land,Fuzhou 344000,China
1 引 言
子午线弧长计算是经典大地测量问题之一[1, 2, 3, 4]，围绕这一问题的计算和应用，近年来各国学者提出了许多新的方法和见解[5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]。因子午线弧长问题涉及椭圆积分，不能直接求出，其经典算法是按二项式定理展开的级数展开，国内学者常采用的形式为[20]
式中
为提高式(2)的收敛速度，文献[8,9]以第二偏心率e′来代换第一偏心率e，式(2)由正项级数转为交错级数。而国际上则多以椭球的第三扁率n(the third flattening)来代换e[1, 3, 4, 14]。其中文献[3, 14]指出在子午线弧长的计算中，以e为参数的收敛性不及以n为参数的收敛性好。另外，文献[10, 11, 12, 13, 14]则论证了子午线弧长与第二类椭圆积分的关系，文献[12]提出调用第二类椭圆积分函数库以达到计算任意精度子午线弧长的建议。以上研究成果丰富了子午线弧长的理论与应用，但迄今尚未有文献给出按二项式定理计算子午线弧长的误差估计理论。本文通过引入高斯超几何函数，对子午线弧长公式进一步简化，并给出其泰勒级数解释，分析其精度。
2 子午线弧长公式的简化引入参数椭球的第3扁率
可得e2=4n/(1+n)2，并由此可得
将其代入式(2)，可得
根据文献sup>[12,13]，子午线弧长公式与高斯超几何函数之间的关系为
式中，F为高斯超几何函数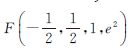
的缩写
对式(1)提取系数A′，由高斯超几何函数F与A′的关系式(6)，式(1)可化为
式中，B″、C″、…、G″等系数仍以n的幂级数形式给出
综合式(7)—式(9)，各系数取至n6，可得
至此，将子午线弧长计算公式(1)及式(2)化为公式(10)，相对简化了其系数结构。
3 子午线弧长公式的泰勒级数解释及其误差估计 3.1 公式的泰勒级数解释由式(1)及式(2)可知，若视子午线弧长S为e的函数S=f(e)(视e为变量)，显然S对e在以e0=0为中心的邻域内无穷可导，因此式(1)在e0=0处可展开为泰勒级数
该泰勒级数通过手工推导展开是较为困难的。笔者在数学软件Mathematica 8.0中实现其级数展开，按下式输入命令并运行 得到结果与式(1)、式(2)完全一致。式中Series[]命令为泰勒级数展开命令，其他各命令功能参见Mathematica手册[24]。
同理，将式(3)代入子午线弧长公式并化简可得
在此基础上，视子午线弧长S为n的函数(视n为变量)，则式(13)在n0=0处可展开为泰勒级数，按式(12)形式在Mathematica8.0中输入相应命令，并提取F，可得到与式(10)完全一致的结果。
以上分析表明按二项式定理展开与按泰勒级数展开求解子午线弧长是统一的，而有了子午线弧长公式的泰勒级数解释，即可按泰勒级数的拉格朗日型余项来估计其误差。
3.2 误差估计为讨论方便，设F=F(n)及
可得S=aFY，则子午线弧长S的解算误差由F的误差和Y的误差两方面引起。记F和Y展开至n6的拉格朗日型余项分别为R6F(n)、R6Y(n)，则有
式中，ξ、ζ分别满足0＜ξ＜n，0＜ζ＜n。F(7)(ξ)、Y(7)(ζ)的表达式为
显然，应用拉格朗日型余项(15)估计误差的关键是确定F(7)(ξ)、Y(7)(ζ)的上限MF、MY。本文取MF、MY为|F(7)(ξ)|、|Y(7)(ζ)|的最大值，下面求之。
因为S=aFY，所以F、Y均收敛，其中F为n的幂级数；对于[0,π/2]内任意的大地纬度值，Y也为n的幂级数，由“收敛的幂级数在其收敛半径内逐项微分所得级数仍收敛[25]”的性质可知F(7)(ξ)、Y(7)(ζ)也均收敛。对于F(7)(ξ)，在区间0,n上，恒有F(7)(ξ)＜0，F(8)(ξ)＞0，所以 (7)(ξ)为单调递增函数，故
对于Y(7)(ζ)，由式(16)可知其为周期性函数，理论上其最小正周期随纬度倍角的增加而趋于无穷小。但事实上，经验证，随着式(16)的展开，其纬度倍角的正弦的系数将逐渐趋于0，sin14B以后各项的周期性影响很小，Y(7)(ζ)的最小正周期趋于π/7。应用多元函数极值分析，可求得其最大值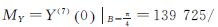
32，具体过程从略。
再由误差传播定律可得
式(17)即为公式(10)的误差估计。
同理，对子午线弧长公式(1)也可作泰勒级数解释，其误差估计为
式中
与F(7)(ξ)情况类似，容易证明Me为收敛的幂级数。类似的，可得展开至其他各阶的误差估计式，结构与上述公式类似，此不赘述。
比较式(17)、式(18)两误差估计式，可得
对地球椭球而言，ΔSn/ΔSe≈1/1.12×104。可见改进后的公式(10)精度提高显著。其主要原因在于：以n替换e，并提取高斯超几何函数后，原公式(1)中各系数由以e为参数的正项级数转换为公式(10)中以n为参数的交错级数，且n仅约为e2的1/4，及至n6项，仅约e12的1/4014，加速了各项系数的收敛速度，从而有效提高了子午线弧长的计算精度。
下面以具体实例进行验证分析。
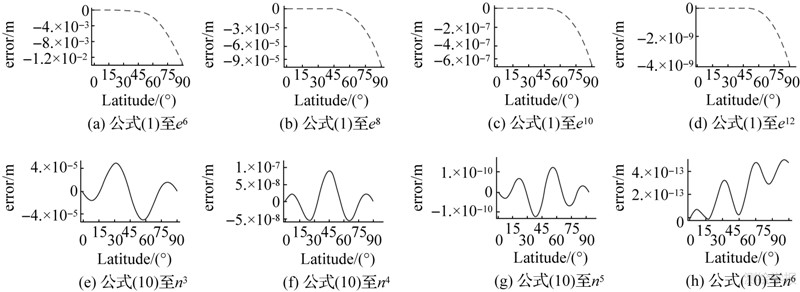
4 算例验证分析为验证公式泰勒级数解释下估计误差的正确性，以WGS-84椭球参数为例，按文献[12]给出的子午线弧长与第二类椭圆积分关系，在Mathematica8.0中调用第二类椭圆积分函数，得到子午线弧长的任意精度解，进而得到分别按公式(1)展开至e6sin6B、e8sin8B、e10sin10B、e12sin12B项及公式(10)展开至n3sin6B、n4sin8B、n5sin10B、n6sin12B项的子午线弧长解算误差，误差对比曲线如图 1所示，最大估计误差与实际最大绝对误差对比列于表 1。
|
| 图 1 子午线弧长解算误差曲线图 Fig. 1 Error curves of the solution of the meridian arc length |
| m | ||||||
| 公式(1) | 公式(10) | |||||
| 阶数 | 最大估计误差 | 实际最大绝对误差 | 阶数 | 最大估计误差 | 实际最大绝对误差 | |
| e6 | 1.78×10-2 | 1.35×10-2 | n3 | 4.79×10-5 | 4.76×10-5 | |
| e8 | 1.32×10-4 | 8.97×10-5 | n4 | 8.89×10-8 | 8.89×10-8 | |
| e10 | 1.00×10-6 | 5.97×10-7 | n5 | 1.23×10-10 | 1.22×10-10 | |
| e12 | 7.69×10-9 | 3.97×10-9 | n6 | 6.87×10-13 | 4.98×10-13 | |
| 注：n4项的最大估计误差为8.886944×10-8m，实际最大误差为8.886899×10-8m，表中数据按四舍五入原则取位。 | ||||||
验算结果表明，按公式(10)分别展开至n3sin6B、n4sin8B、n5sin10B、n6sin12B项比按公式(1)分别展开至e6sin6B、e8sin8B、e10sin10B、e12sin12B项的精度提高了3～4个数量级，精度提高显著，且验算误差与估计误差吻合，验证了按泰勒级数解释所给误差估计理论的正确性。
5 结 语本文通过引入新的参数，得到了子午线弧长的简化形式，加快了收敛速度，精度提高显著，体现了高斯超几何函数的引入对子午线弧长在公式简化及精度提高方面的意义，而本文给出的子午线弧长公式的泰勒级数解释则给子午线弧长公式的误差分析提供了理论依据。
| [1] | TORGE W. Geodesy[M]. 3rd ed. Berlin: Walter De Gruyter, 2001: 91-98. |
| [2] | KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2001: 64-73. (孔祥元,郭际明,刘宗泉. 大地测量学基础[M]. 武汉:武汉大学出版社,2001:64-73.) |
| [3] | HELMERT F R. Die Mathematischen und Physikalischen Theorien der Hheren Geodsie (English Translation Version) [M]. Leipzig: Printing and Publishing House of B.G. Teubner, 1880: 46-48. |
| [4] | DEAKIN R E, Hunter M N. Geometric Geodesy: Part A [R]. Melbourne: RMIT University, 2010: 60-77. |
| [5] | DING Jiabo. The Transforming the Zones of Gauss Projection from Latitudes of Low Points[J]. Acta Geodaetica et Cartographica Sinica, 1993, 22(3): 212-217. (丁佳波. 利用底点纬度进行高斯投影换代计算[J]. 测绘学报, 1993, 22(3): 212-217.) |
| [6] | LI Houpu, BIAN Shaofeng. The Expressions of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 5-9. (李厚朴,边少峰. 高斯投影的复变函数表示[J]. 测绘学报,2008,37(1): 5-9.) |
| [7] | YANG Yuanxi. The Respective Roles and Contributions of Various Observation in Integrated Geodesy[J]. Acta Geodaetica et Cartographica Sinica, 1989,18(3):232-238. (杨元喜. 整体大地测量中各类观测值的分工与贡献[J]. 测绘学报,1989,18(3): 232-238.) |
| [8] | CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(3): 189-194. (程鹏飞,成英燕,文汉江, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3): 189-194.) |
| [9] | LIU Zhengcai. Simplification of Formula of Meridian Arc Length & Program of Gauss Projection[J]. Engineering of Surveying and Mapping, 2001, 10(1):55-56. (刘正才. 子午线弧长公式的简化及通用高斯投影计算程序介绍[J]. 测绘工程, 2001, 10(1): 55-56.) |
| [10] | DORRER E. From Elliptic Arc Length to Gauss- Krüger Coordinates by Analytical Continuation [C]//Geodesy: The Challenge of the 3rd Millennium. Berlin: Springer, 2003: 293-298. |
| [11] | BERMEJO-SOLERA M, OTERO J. Simple and Highly Accurate Formulas for the Computation of Transverse Mercator Coordinates from Longitude and Isometric Latitude[J]. Journal of Geodesy, 2009, 83: 1-12. |
| [12] | GUO Jiachun, ZHAO Xiuxia, XU Li, etal. Calculating Meridian Arc Length by Transforming Its Formula into Elliptic Integral of Second Kind[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 94-98. (过家春,赵秀侠,徐丽,等. 基于第二类椭圆积分的子午线弧长公式变换及解算[J]. 大地测量与地球动力学,2011,31(4): 94-98.) |
| [13] | GUO Jiachun. New Method for Inverse Solution of Meridian Based on Elliptic Integral of the Second Kind[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 116-120. (过家春. 基于第二类椭圆积分的子午线弧长反解新方法[J]. 大地测量与地球动力学,2012,32(3): 116-120.) |
| [14] | KAWASE K. A General Formula for Calculating Meridian Arc Length and Its Application to Coordinate Conversion in the Gauss-Krüger Projection[J]. Bulletin of the Geospatial Information Authority of Japan, 2011, 59: 1-13. |
| [15] | YI Weiyong, BIAN Shaofeng, ZHU Hanquan. Determination of Foot Point Latitude by Analytic Positive Series[J]. Journal of Institute of Surveying and Mapping, 2000, 17(3): 167-171. (易维勇,边少峰,朱汉泉. 子午线弧长的解析型幂级数确定[J]. 测绘学院学报,2000,17(3): 167-171.) |
| [16] | LIU Renzhao, WU Jicang. Recursive Computation of Meridian Arc Length with Discretionary Precision[J]. Journal of Geodesy and Geodynamics, 2007, 27(5): 59-62. (刘仁钊,伍吉仓. 任意精度的子午线弧长递归计算[J]. 大地测量与地球动力学,2007,27(5): 59-62.) |
| [17] | BIAN S F, CHEN Y B. Solving an Inverse Problem of a Meridian Arc in Terms of Computer Algebra System[J]. Journal of Surveying Engineering, 2006, 132(1):7-10. |
| [18] | NIU Zhuoli. Formulae for Calculation of Meridian Arc Length by the Parameters of Space Rectangular Coordinates[J]. Bulletin of Surveying and Mapping, 2001(11): 14-15. (牛卓立. 以空间直角坐标系为参数的子午线弧长计算公式[J]. 测绘通报,2001(11): 14-15.) |
| [19] | LIU Xiushan. Numerical Integral Method Calculating Meridian Arc Length[J]. Bulletin of Surveying and Mapping, 2006(5): 4-6. (刘修善. 计算子午线弧长的数值积分法[J]. 测绘通报, 2006(5): 4-6.) |
| [20] | CHENG Pengfei, CHENG Yingyan, WEN Hanjiang, et al. Practical Manual on CGCS2000[M]. Beijing: Surveying and Mapping Press, 2008: 147-148. (程鹏飞,成英燕,文汉江, 等. 2000国家大地坐标系实用宝典[M]. 北京:测绘出版社,2008: 147-148.) |
| [21] | LIU Shishi, LIU Shida. Special Function[M]. Beijing: China Meteorological Press, 1988: 656-745. (刘式适,刘式达. 特殊函数[M]. 北京:气象出版社,1988:656-745.) |
| [22] | ZHU Huatong. Review on the Methods for Calculating Latitude of Low Points[J]. Bulletin of Surveying and Mapping, 1978(5): 10-14. (朱华统. 底点纬度计算方法评述[J]. 测绘通报,1978(5): 10-14.) |
| [23] | SUN Qun, YANG Qihe. The Research on the Computation of the Foot-point Latitude and the Inverse Solution of Isometric Latitude and Function[J].Journal of Institute of Surveying ang Mapping,1985(2):64-75. (孙群,杨启和. 底点纬度解算以及等量纬度和面积函数反解问题的探讨[J]. 测绘学院学报,1985(2): 64-75.) |
| [24] | WOLFRAM S. The Mathematica Book[M]. 5th ed. Champaign: Wolfram Media Inc, 2003. |
| [25] | BRONSHTEIN I N, SEMENDIAEY KA, HIRSCH K A. Handbook of Mathematics[M]. 4th ed. New York: Van Nostrand Reinhold, 2003: 412-416. |