2. 河海大学 文天学院,安徽 马鞍山 243000
2. Wentian College, Hohai University, Maanshan 243000, China
森林是最大的有机碳存贮库,也是控制陆地生物圈能量传输的一个重要组成部分,而森林植被高度则是管理和研究森林的一个重要参数[1, 2]。在众多的植被高度提取方法中,极化干涉SAR技术因具有比其他植被提取技术更多的优势而获得巨大的发展。该技术将极化信息和干涉相位信息有效地结合,既发挥了干涉SAR技术对地表植被散射体的空间垂直分布和高度具有较高敏感性的优势,又综合了极化SAR技术对植被散射体的形状和方向具有较高敏感性的特点[3]。因此基于极化干涉SAR技术提取地表植被高度是当前极化干涉研究的热点问题之一。
极化干涉SAR植被高度反演的关键是能够区分植被底部和顶部差异的散射特征分量,从而获取植被顶部的相位中心以及底部地表的相位中心。基于此,学者们提出了两类典型的极化干涉SAR植被参数反演方法:①基于复相干系数相位、复相干幅度联合反演算法,主要包括:六维非线性迭代反演算法[4]、三阶段反演算法[5, 6]及复数域最小二乘平差反演算法[7];②基于复相干系数的相位反演算法,主要包括DEM差分算法[8]及基于ESPRIT(旋转不变技术)的植被高度反演算法[9, 10]。此外,针对ESPRIT算法存在地面散射相位估计不准的问题,本文作者提出一种改进的ESPRIT算法[11]。通过后续大量研究试验发现,尽管对ESPRIT算法进行了改进,但是基于相位信息的反演算法的稳健性低于相位与相干幅度联合反演算法。原因在于前者忽略了相干幅度,未能很好地考虑植被散射物理特性。三阶段算法是目前相位与相干幅度联合反演算法中较常用的方法。然而,在三阶段方法中,植被高反演精度容易受到地面散射相位估计误差的影响[12]。
针对这一关键问题,本文提出基于极化干涉互协方差矩阵分解的植被高度反演方法。该方法首先利用Freeman-Durden分解理论[13, 14]和极化干涉互协方差矩阵[15, 16],估计出更准确的地面散射相位;然后,结合RVoG模型[17, 18]反演植被高度;最后,利用欧空局(ESA)的软件PolSARpro模拟的L波段极化干涉SAR数据和亚马逊森林地区的ALOS PALSAR L波段数据进行试验验证。
2 极化干涉互协方差矩阵分解极化干涉SAR由主、从全极化雷达构成,假定主影像和从影像的极化散射矢量分别为
式中,Spqi表示极化散射矩阵元素,i=1,2分别表示主、从雷达影像,p、q分别表示雷达天线接收和发射的极化方式,其中h代表水平极化,v代表垂直极化。通过公式〈k1L(k2L)*T〉就能得到极化干涉SAR互协方差矩阵Ct。根据文献[13]和文献[16]提出的基于Freeman的极化干涉SAR互协方差矩阵分解理论,Ct可以分解成3个分量组成,即体散射矩阵Cv、表面散射矩阵Cs和二面角散射矩阵Cd,分别对应3种不同的物理散射机制,其表达式为
对于主、从两幅影像,散射系数的幅度不会改变,但是相位是不同的。这个相位差主要是来自两方面的贡献:不同极化通道下复散射系数之间的差值ψpi-ψqi;垂直坐标中与位置相关的干涉相位Δvp。但是在这里同时假设对于所有的极化通道体散射机制的有效相位中心是相同的[13],那么矩阵Cv就表示为
令Fv=(3π/4)ejΔvp,式(3)即简化为同样,表面散射矩阵表达式为
式中,Δsp表示表面散射机制的相位中心;Δsψvh表示主、从影像中不同极化通道之间的相位差。令Fs=
 ,定义β=
,定义β= ,这样Cs矩阵就简化为
,这样Cs矩阵就简化为
同样,二面角散射矩阵表达式为
式中,Δdp表示二面角散射机制的相位中心;Δψvh表示不同极化通道下复散射系数之间的差值。同样,令
 ,定义
,定义 。其中,Rgv、Rtv、Rgh和Rth是Fresnet反射系数[13],下标字母g代表的是地面,t代表树干,而v和h代表不同的极化方式。同时假设对于主影像和从影像这些系数是相等的[13],则Cd矩阵表示为
。其中,Rgv、Rtv、Rgh和Rth是Fresnet反射系数[13],下标字母g代表的是地面,t代表树干,而v和h代表不同的极化方式。同时假设对于主影像和从影像这些系数是相等的[13],则Cd矩阵表示为
由式(2)可知Ct矩阵中的每个元素表示为
从式(9)中可以看出,体散射成分贡献可以直接从C22中得到。去除体散射成分贡献之后,剩余部分用Cr表示
则可以通过对式(10)的优化处理来获得参数的估计值。式(10)表示的实质是一个非线性最小二乘问题,可以利用非线性最小二乘求解方法进行求解,最后得到3种不同散射机制的有效相位中心。通过分析,二面角散射机制相位中心位于植被根部树干和地面交互处[15],在植被覆盖区域二面角散射机制相位中心基本位于地面,因此可以把二面角散射机制相位作为地面散射相位[19]。同时,体散射机制相位中心位于植被冠层,而表面散射机制相位中心位于植被冠层顶部,故可以将表面散射机制相位中心与二面角散射机制相位中心之差认为是由植被高度引起的相位变化,然后利用相位高度转换关系得到植被高度。
3 改进的反演算法研究表明利用极化干涉互协方差矩阵分解算法所得到的植被高度相对于实际植被高度偏低[16],究其原因是由于树冠顶层相位估计不准,但是该方法对于地面散射相位估计相对可靠。经典三阶段反演算法中利用多个极化通道的复相干系数观测值在复数平面内的直线拟合获得的地面散射相位往往不准确,进而影响植被高度估计的精度。因此,本文利用Freeman-Durden分解理论和极化干涉互协方差矩阵,估计出更准确的二面角散射机制的相位作为地面散射相位,然后,结合随机体-地表散射(RVoG) 模型反演植被高度,从而提高植被高度反演的精度。
目前,极化干涉SAR植被高度反演最常用且有效的是RVoG模型,假设植被体由随机方向的粒子组成,与极化方式无关,将植被场景认为是由地面和植被构成的二层模型。根据文献[17,18],在RVoG散射模型中,复干涉相干系数可以表示为
式中,mw表示有效地面散射与体散射回波的幅度比,w是表示与极化有关的单位矢量,mw=0时, 变成只有体散射模型的相干系数,mw→∞时,
变成只有体散射模型的相干系数,mw→∞时, 变成地面散射模型的相干系数;Φ表示地面散射相位;
变成地面散射模型的相干系数;Φ表示地面散射相位; v是仅有植被体引起的体散射相干系数,其表达式为
v是仅有植被体引起的体散射相干系数,其表达式为
式中,kz是距离向谱滤波后的有效垂直干涉波数;σ是植被消光系数;θ0是雷达入射角;hv表示植被高度。
从式(11)和式(12)可以看出,地面散射相位Φ精确估计是基于RVoG模型植被高度准确估计的关键因素之一。本文根据极化干涉互协方差矩阵分解算法和三阶段算法的特点,提出了一种新的植被高度反演算法,该算法具体思路如下:
(1) 首先利用极化干涉互协方差矩阵分解,通过非线性最小二乘方法得到3种不同散射机制的有效相位中心,其中二面角散射机制的相位中心位于地表与树根底部交界处,与地面散射相位位置大致相同。
(2) 将极化干涉互协方差矩阵分解得到的二面角散射机制的相位作为地面散射相位Φ的估计值。
(3) 给定植被高度及消光系数可能的数值范围,利用RVoG模型中体相干性计算公式,计算出该范围内可能的体去相干系数的预测值,从而建立了体相干系数查找表(look up table,LUT)。
(4) 假定hv极化方式不存在地面贡献,结合地面散射相位的估计值Φ计算对应体相干系数观测值与步骤(3)得到的查找表中所有模型预测值的均方差。将最小均方差对应的植被高度作为最后植被高度的估值,具体公式如下
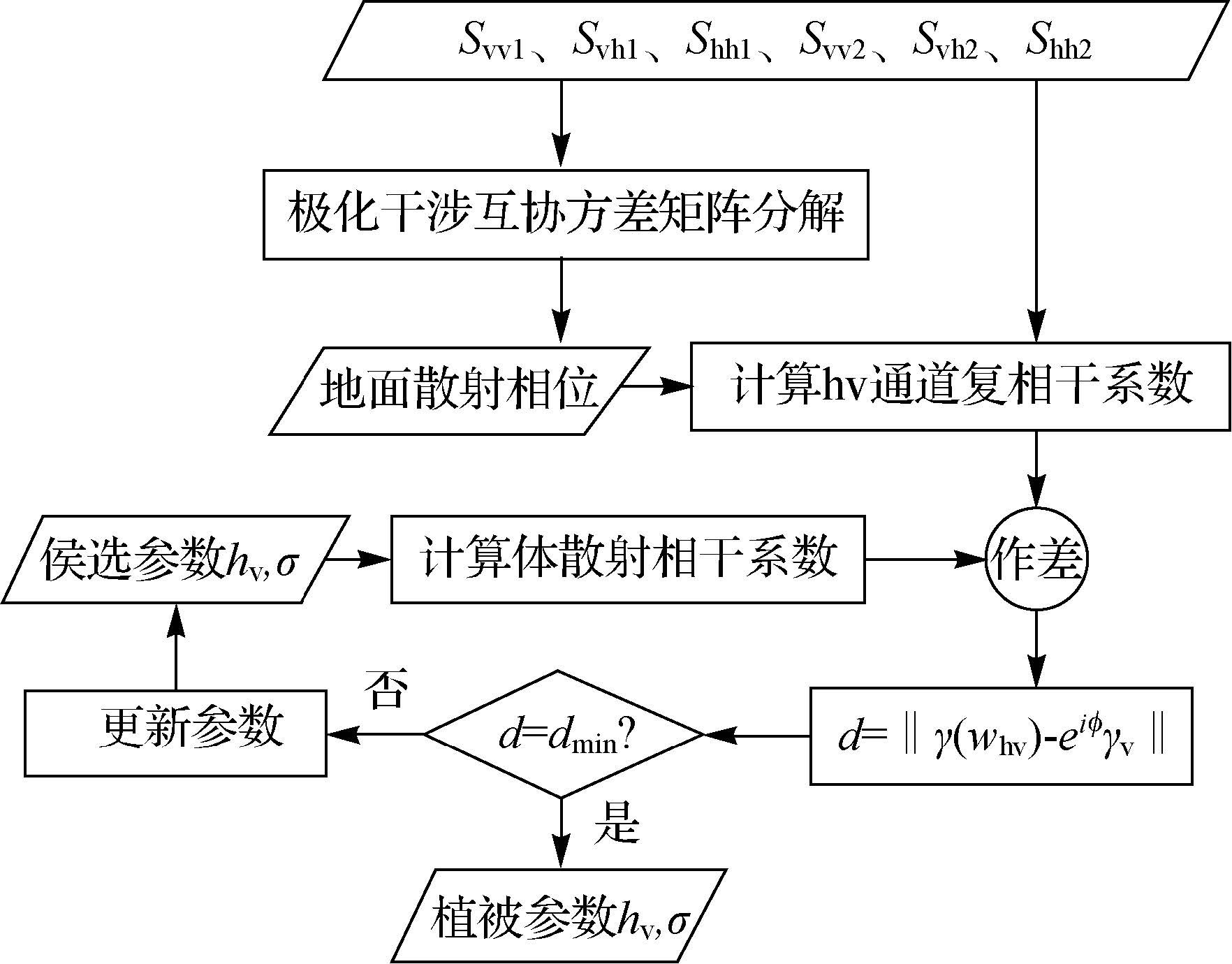
由植被高度反演新算法构建思路可以看出,改进的算法有效地避免了利用极化干涉互协方差矩阵分解算法直接得到的植被高度由于树冠顶层相位估计不准引起的偏差,也克服了经典三阶段法进行植被高度反演时由于地面散射相位估计不准引起的偏差,从而有效地提高了反演的精度。图 1所示的是改进算法的流程图。
4 试验及结果分析 4.1 模拟数据试验结果及分析试验中所采用的一组L波段全极化干涉数据是由欧空局(ESA)的软件PolSARpro中PolSARpro Simulator模块[20]进行模拟所生成。用户可以根据具体需要设置传感器参数(平台高度、基线、入射角、波长等)及地表参数(粗糙度、坡度、水分、植被类型、密度等),软件根据这些参数生成主、从两幅全极化数据。此外,用户可以利用该软件提供的极化干涉模块进行极化干涉SAR数据处理。对于本文模拟数据的参数见表 1。
|
| 图 1 改进算法流程图 Fig. 1 The flow chart of the modified algorithm |
| 平台高度/m | 入射角/(°) | 垂直基线/m | 方位分辨率/m | 斜距分辨率/m | 树种 | 植被密度/(stems/ha) | 植被高度/m |
| 3674.235 | 30° | -6.1 | 1.0 | 0.5 | Hedge | 360 | 10 |
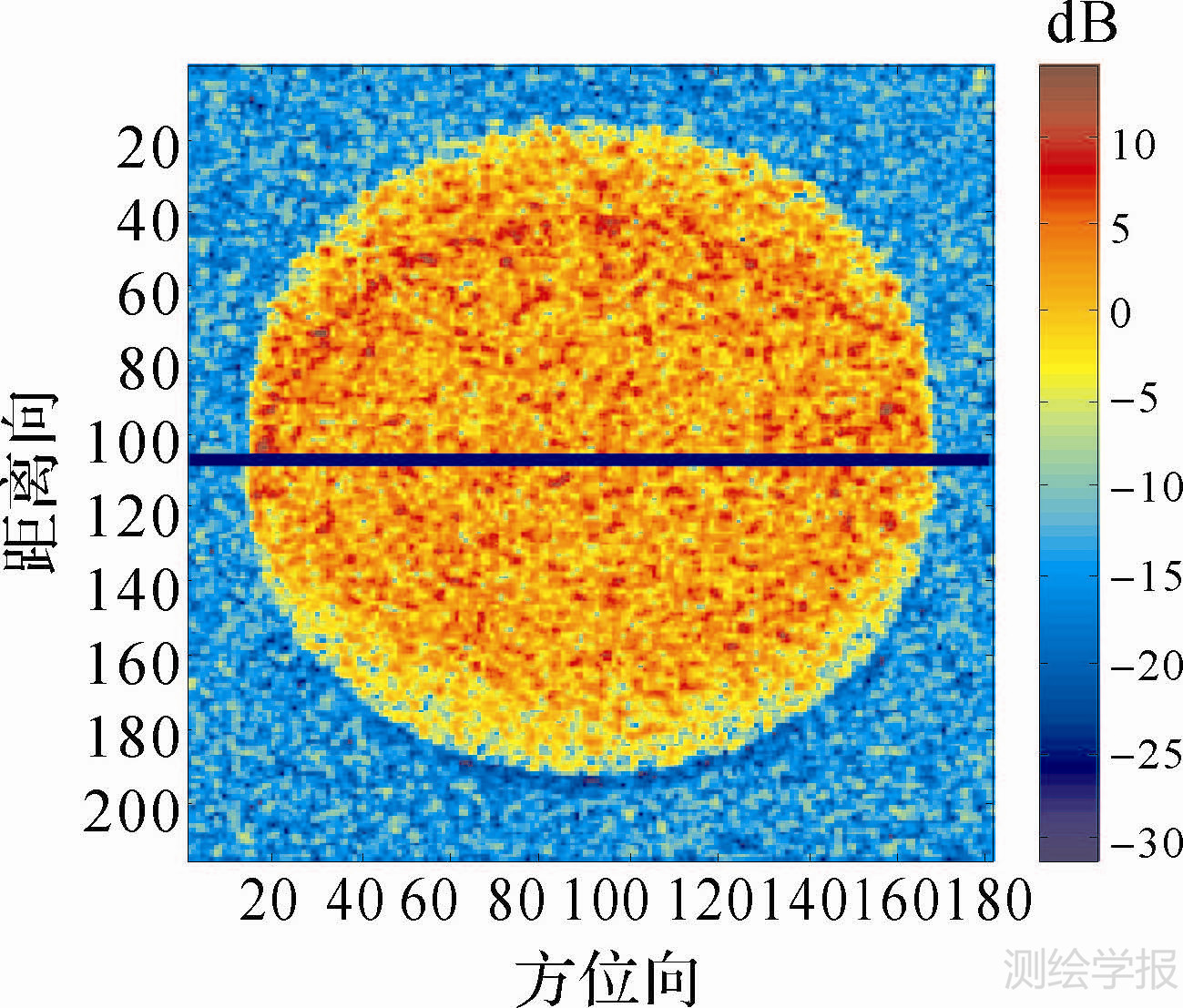
图 2所示的是主影像的功率图像,从图中可以看出中间圆形区域是高度为10m的植被覆盖区域,其他区域为非植被覆盖的地表。图中在方位向标注的蓝色线段用于下文的分析,本文提出的植被高度反演算法及数据分析是以Matlab为开发平台编程实现。
图 3所示的是极化干涉互协方差矩阵分解得到3种不同散射机制有效相位中心。从图中可以看出3种不同散射机制相位中心位置是垂直分布的。表面散射贡献主要来自于植被上层,体散射贡献主要来自于植被冠层。但是有些区域表面散射相位位置要低于体散射相位位置,分析可能有两点原因:①与树的种类有一定的关系,对于树顶树叶较小的树(针叶林),其表面散射有可能要低于体散射,而对于树叶茂盛的树表面散射要高于体散射;②与试验数据的波长有关,波段越长穿透性越强。二面角散射机制相位中心位于地面[19],在植被区域与非植被区域交界处,二面角散射机制比较明显,其相位中心位置变化趋势明显。从试验结果看,试验区体散射机制相位中心比较稳定,表面散射机制相位中心有变化起伏,但总的来说表面散射机制相位中心位置位于植被顶层,因此由表面散射机制相位中心和二面角散射机制相位中心之间的相位差可以估计得到植被高度。
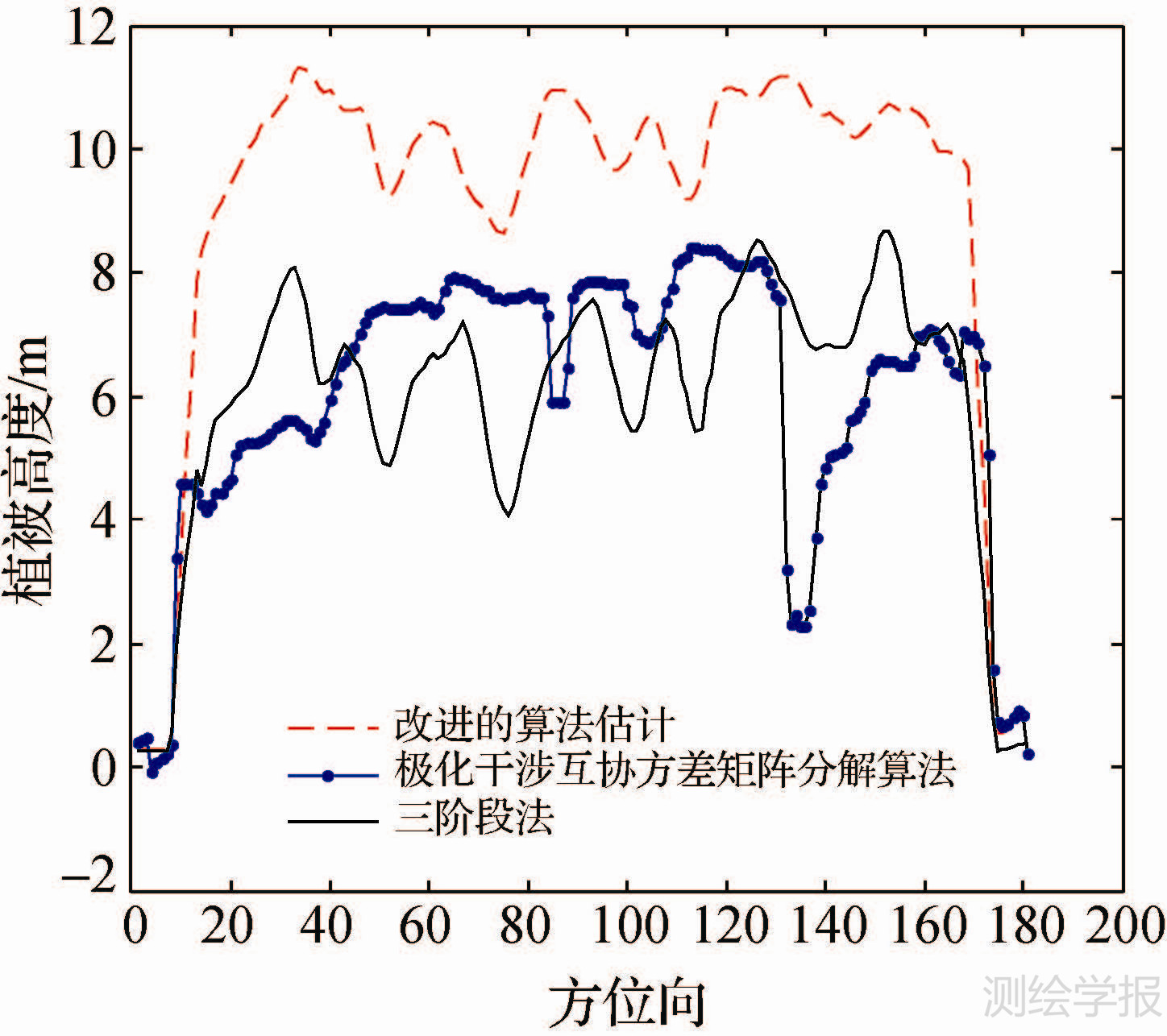
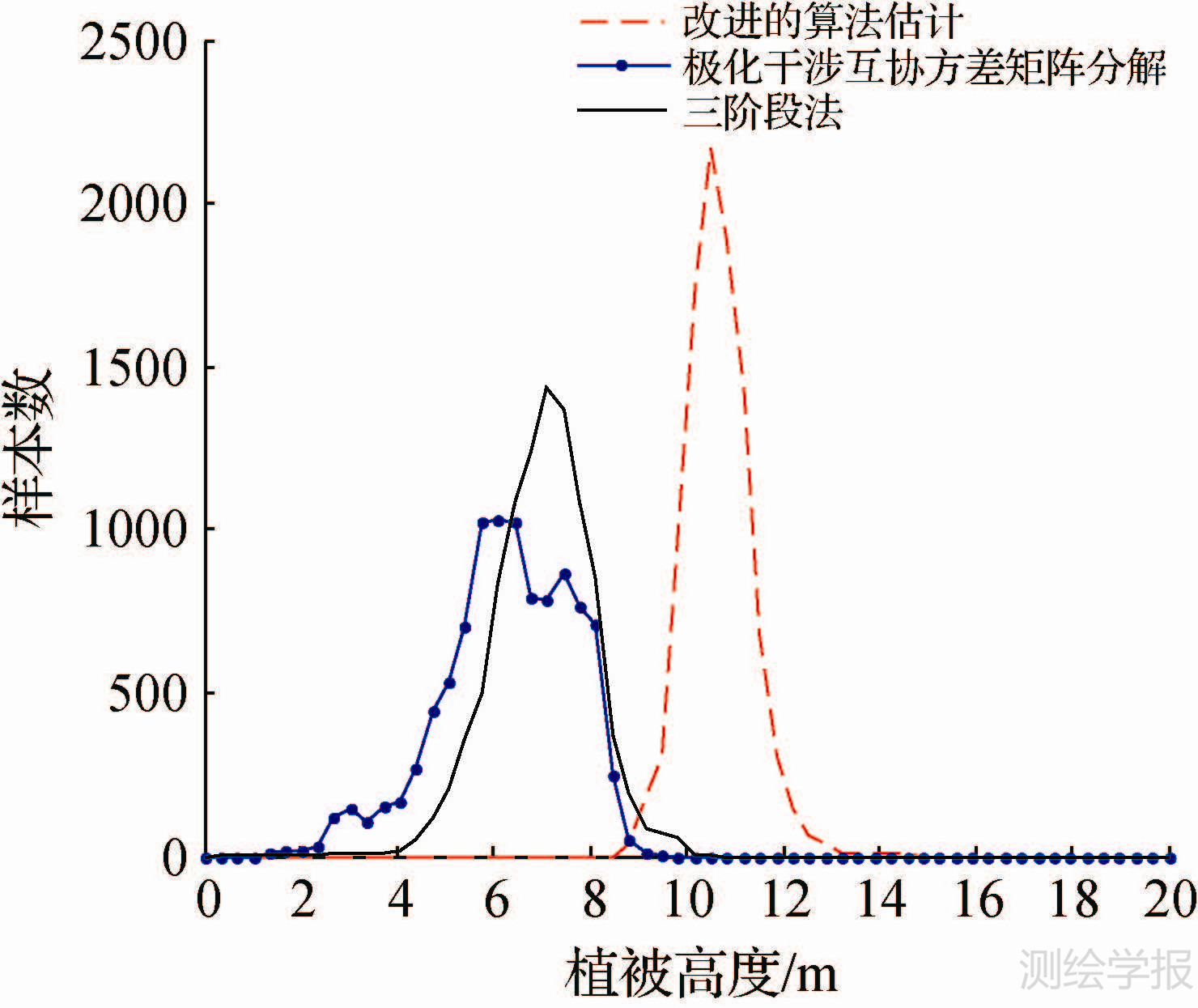
由图 4和图 5可以直观地看出,由表面散射机制相位中心和二面角散射机制相位中心之间的相位差所估计出的植被高度相对于实际植被高度来说精度不高,比10m的理论高度要偏低,同样三阶段法得到的植被高度精度也不高。相比之下,改进算法估计出的植被高度精度得到较好的改善。对于植被区域统计得到:直接利用极化干涉互协方差矩阵分解算法估计出的植被高度均值为6.3m,均方根误差为4.0m;三阶段法估计出的植被高度均值为7.01m,均方根误差为3.16m;而改进算法估计出的植被高度均值为10.66m,均方根误差为0.95m。由此证明,改进算法反演出的平均植被高度更接近理论高度,进而说明改进算法的可行性,提高了植被高度反演的精度。
|
| 图 2 主影像功率图 Fig. 2 Master span image |

|
| 图 3 图 2标注方位线处3种不同散射机制相位中心高度估计图 Fig. 3 Image for three different scattering mechanisms phase center of the marked azimuth line in Fig. 2 |
|
| 图 4 算法改进前后图 2中标注方位向处的反演高度比较 Fig. 4 Comparision of the retrieved heights of the marked azimuth line in Fig. 2 |
|
| 图 5 改进前后植被高度的直方图比较 Fig. 5 The histogram of vegetation heights comparision between traditional algorithm and the proposed algorithm |
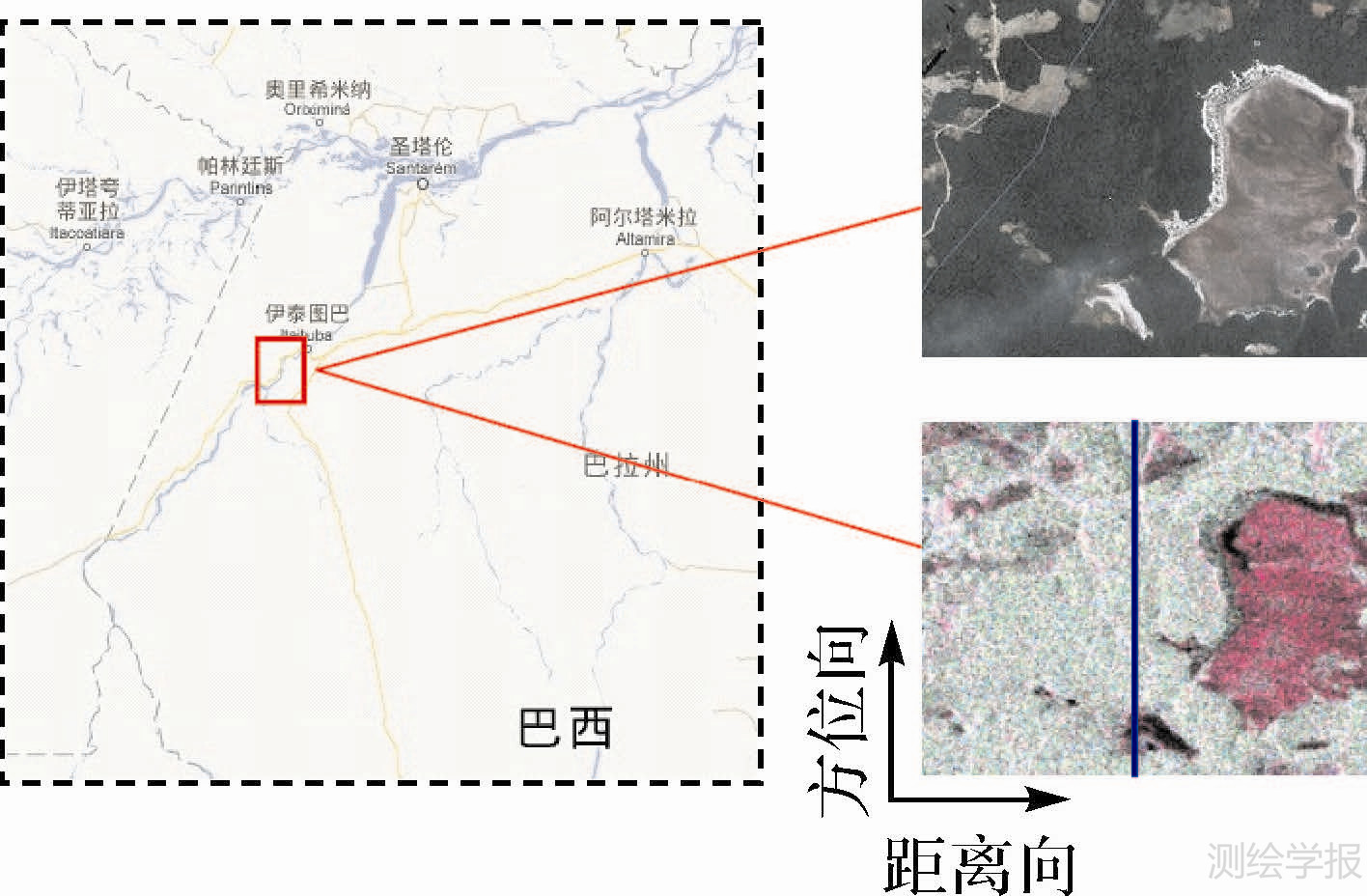
为验证本文算法对于真实数据的可行性,利用一组星载极化干涉SAR数据进行了试验。数据为日本ALOS卫星PALSAR传感器在亚马逊热带雨林区获取的L波段重复轨道极化SAR数据,研究区域的中心地理经纬度分别是4.450°S,56.317°W。主、从两景影像获取的时间分别为2007-03-13和2007-04-28,垂直基线为120m,时间基线为46d,入射角为24.0808°,斜距向采样间隔为9.4m,方位向采样间隔为3.6m。图 6所示的是所裁剪的研究区域的卫星地图、光学遥感影像(Google Earth)和Pauli分解图。在光学影像中解译出绿色代表植被区域,其他的是非植被区域,同样在Pauli分解图中绿色代表是植被,红色代表是裸地。该区域植被相对比较稀疏,由光学遥感影像解译知,其可能是由人为砍伐导致。植被为典型的热带雨林阔叶乔木,由美国国家航天航空局(NASA)提供的3D Global Vegetation Map可以知道该区域的植被平均高度大约为30m[21]。Pauli分解图中沿方位向标定的蓝色线段用于后文分析。
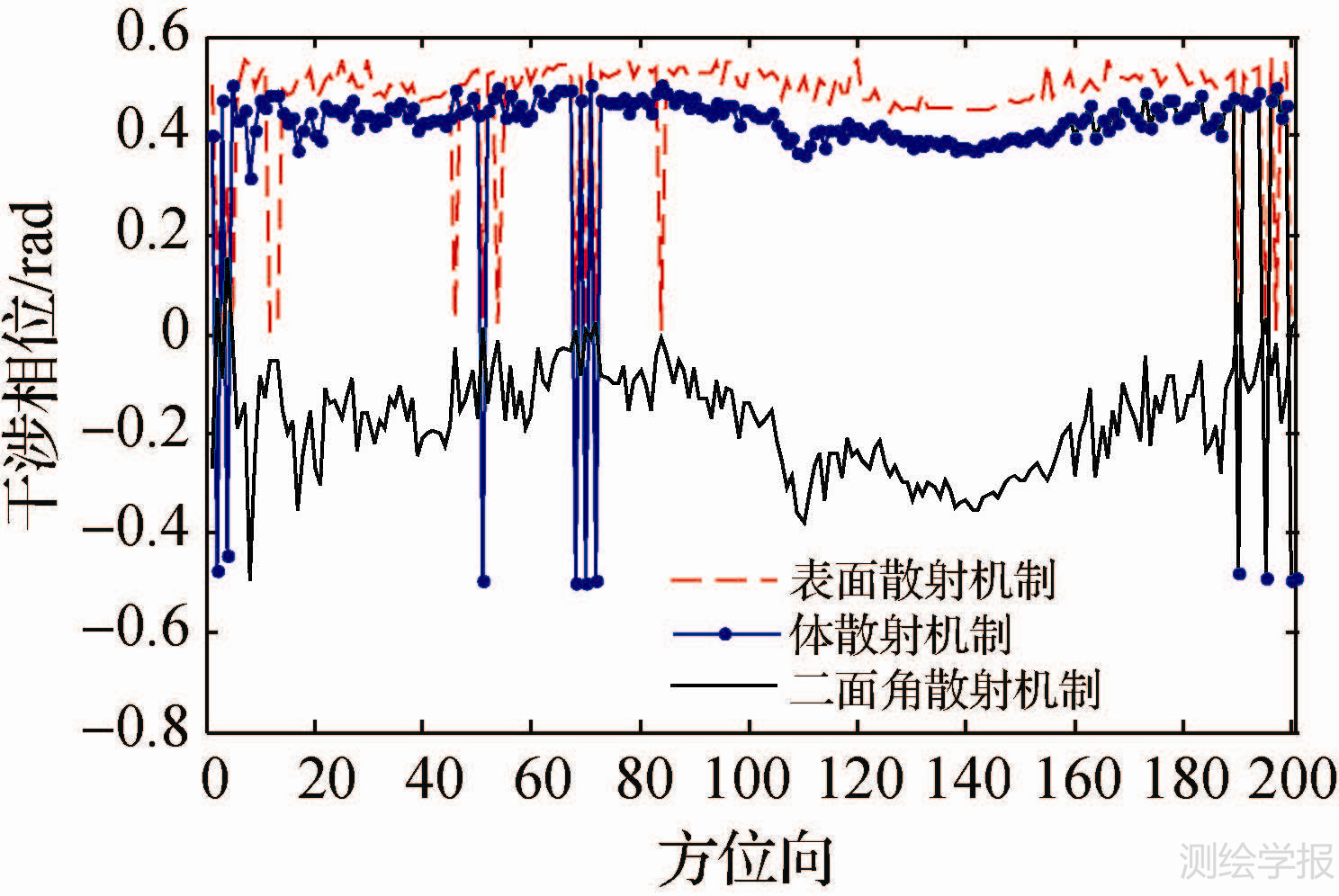
图 7所示的是图 6中蓝色直线标定区域的剖面图。从图 7纵向剖面图中可以直观地看出植被分布相对一致,高度趋势大体一致:植被覆盖区表面散射相位中心位置要高于体散射相位中心位置,在植被相对稀疏处,地面也有对表面散射机制的贡献;二面角散射机制相位中心位于地面附近,地面和植被之间相互作用的二面角散射机制相对明显,而在植被浓密处,二面角散射机制比较稳定;有些区域体散射机制存在一些误差,位于地面以下(见图 7蓝色曲线对应的负值)。总体上二面角散射机制相位中心变化趋势比较符合地面变化趋势,因为所选的研究区域地面是比较平坦的,地形起伏较小。
|
| 图 6 研究区域地理位置 Fig. 6 Geographical position of the study area |
|
| 图 7 图 6标注方位向处3种不同散射机制相位中心高度估计图 Fig. 7 Image for three different scattering mechanisms phase center of the marked azimuth line in Fig. 6 |
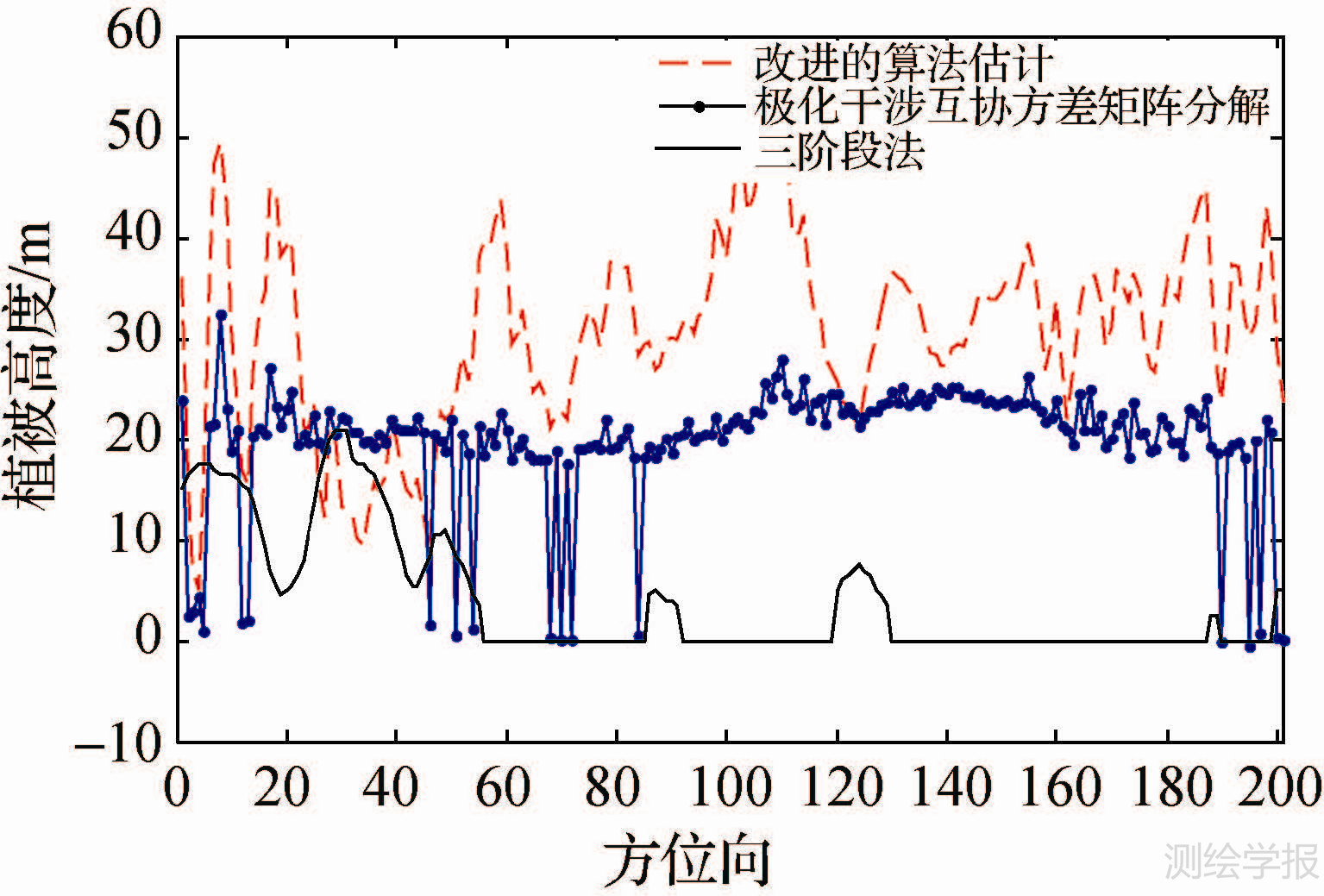
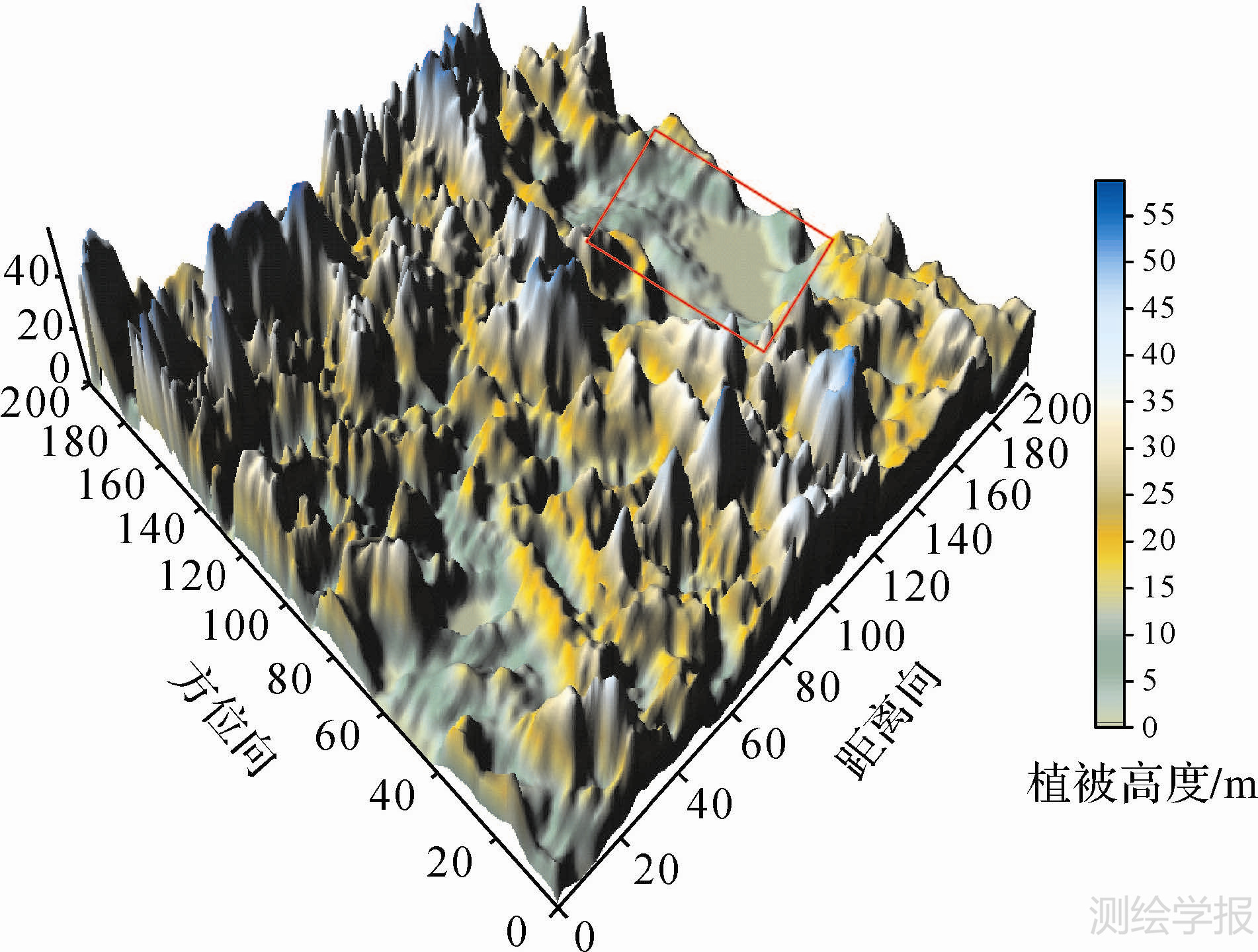
图 8和图 9所示的分别是3种算法反演植被高度所得到的剖面图和改进算法的三维透视图。由图 8中可以看出,三阶段法反演的植被高度最低,在植被稀疏的地方甚至无法得到反演结果,导致平均高度严重偏低,并且在裸地区域也没有很好地反演出来,与实际情况不相符合,因此三阶段法对于植被比较稀疏的区域反演的效果较差。主要原因是:在植被稀疏或者裸地区域,不同的极化方式所对应的相位中心比较集中,因此三阶段法中利用最小二乘直线拟合估计地面散射相位时误差较大[22]。相比较三阶段法,改进算法反演的植被高度与实际更相符合,并且对于植被稀疏的区域也能反演出较为准确的结果。与此同时,对于裸地区域也能较为准确地反演出地形变化趋势(图 9中红色矩形标定区域)。对于植被区域,计算统计出三阶段法反演的平均植被高度是5.67m,极化干涉互协方差矩阵分解直接得到的平均植被高度是23.38m,而改进的算法反演出的平均植被高度为27.24m。这与实际情况是相符合的,进而说明改进算法的有效性,反演的精度比较高。此外,该方法对于植被稀疏的区域反演同样有效,弥补了三阶段法的不足之处。
|
| 图 8 算法改进前后图 6中标注方位向处的反演高度比较 Fig. 8 Comparision of the retrieved heights of the marked azimuth line in Fig. 6 |
|
| 图 9 改进算法反演植被高度三维图 Fig. 9 Three dimentional diagram of vegetation heights using proposed algorithm |
本文针对经典三阶段植被高度反演算法中地面散射相位的估计不准确这一关键问题,提出基于极化干涉互协方差矩阵分解的植被高度反演方法。通过模拟及真实的极化干涉SAR数据试验,结果表明本文提出的算法估计的地表散射相位更可靠,提取的植被高度相比经典三阶段法精度更高,特别对于植被稀疏区域反演的效果更为显著,从而验证了算法的有效性和可靠性。
| [1] | LUO Huanmin, CHEN Erxue, CHEN Jian, et al. Forest Height Estimation Methods Using Polarimetric SAR Interferometry[J]. Journal of Remote Sensing, 2010, 14(4): 806-813. (罗环敏, 陈尔学, 陈建, 等. 极化干涉SAR森林高度反演方法研究[J]. 遥感学报, 2010, 14(4): 806-813.) |
| [2] | GARESTIER F, DUBOIS-FERNANDEZ P C, PAPATHANASSIOU K P. Pine Forest Height Inversion Using Single-pass X-band PolInSAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 59-68. |
| [3] | GUO Huadong, LI Xinwu, WANG Changlin, et al. Polarimetric SAR Interferometry Mechanism and Function[J]. Journal of Remote Sensing, 2002, 6(6): 401-405. (郭华东, 李新武, 王长林, 等. 极化干涉雷达遥感机制及作用[J]. 遥感学报, 2002, 6(6): 401-405.) |
| [4] | PAPATHANASSIOU K P, CLOUDE S R. Single-baseline Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352-2363. |
| [5] | CLOUDE S R, PAPATHANASSIOU K P. Three-stage Inversion Process for Polarimetric SAR Interferometry[J]. IEEE Proceedings: Radar, Sonar and Navigation, 2003, 150(3): 125-134. |
| [6] | TAN Lulu, CHEN Bing, YANG Ruliang. Improved Three-stage Algorithm of Tree Height Retrieval with PolInSAR Data[J]. Journal of System Simulation, 2010, 22(4): 996-999. (谈璐璐, 陈兵, 杨汝良. 利用PolInSAR数据反演植被高度的改进三阶段算法[J]. 系统仿真学报, 2010, 22(4): 996-999.) |
| [7] | ZHU Jianjun, Xie Qinghua, ZUO Tingying, et al. Criterion of Complex Least Squares Adjustment and Its Application in Tree Height Inversion with PolInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 45-51. (朱建军, 解清华, 左廷英, 等. 复数域最小二乘平差及其在PolInSAR植被高度反演中的应用,测绘学报, 2014, 43(1): 45-51.) |
| [8] | CLOUDE S R, PAPATHANASSIOU K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551-1565. |
| [9] | YAMADA H, YAMAGUCHI Y, KIM Y. Polarimetric SAR Interferometry for Forest Analysis Based on the ESPRIT Algorithm[J]. IEICE Transactions on Electronics, 2001, 84(12): 1917-1924. |
| [10] | TAN Lulu, YANG Libo, YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 296-300. (谈璐璐, 杨立波, 杨汝良. 基于ESPRIT算法的极化干涉SAR植被高度反演研究[J]. 测绘学报, 2011, 40(3): 296-300.) |
| [11] | SONG Guiping, ZUO Tingying, WANG Changcheng, et al. A New Vegetation Height Estimation Method Based on Scattering Mechanism Decomposition and ESPRIT Algorithm[J]. Modern Surveying and Mapping, 2013, 36(5): 6-10. (宋桂萍, 左廷英, 汪长城, 等. 基于散射机制分解的ESPRIT植被高度反演新方法[J]. 现代测绘, 2013, 36(5): 6-10.) |
| [12] | LI Tingwei, HUANG Haifeng, LIANG Diannong, et al. A Novel Vegetation Parameters Inversion Method Based on the Freeman Decomposition[J]. Journal of Electronics & Information Technology, 2011, 33(4): 781-786. (李廷伟, 黄海风, 梁甸农, 等. 基于Freeman分解的植被参数反演新方法[J]. 电子与信息学报, 2011, 33(4): 781-786.) |
| [13] | FREEMAN A, DURDEN S L. A Three-component Scattering Model for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551-1565. |
| [14] | AN Wentao, CUI Yi, YANG Jian. Three-component Model-based Decompositon for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2732-2739. |
| [15] | NEUMANN M, FERRO-FAMIL L, REIGBER A. Estimation of Forest Struture, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1086-1104. |
| [16] | BALLESTER-BERMAN J D, LOPEZ-SANCHEZ J M. Applying the Freeman-Durden Decomposition Concept to Polarimetric SAR Interferometry[J]. IEEE Transaction on Geoscience and Remote Sensing, 2010, 48(1): 466-478. |
| [17] | LI Zhen, GUO Ming. A New Three-stage Inversion Procedure of Forest Height with the Improved Temporal Decorrelation RVOG Model[C]//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich: IEEE, 2012: 5141-5144. |
| [18] | GARESTIER F, LE TOAN T. Forest Modeling for Height Inversion Using Single-baseline InSAR/Pol-InSAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1528-1539. |
| [19] | WILSEN C B, SARABANDI K, LIN Y C. The Effect of Tree Architecture on the Polarimetric and Interferometric Radar Responses[C]//Proceedings of 1998 IEEE International Geoscience and Remote Sensing Symposium. Seattle: IEEE, 1998: 1499-1501. |
| [20] | POTTIER E, FERRO-FAMIL L, ALLAIN S, et al. PolSARpro V3.3: The Educational Toolbox for Polarimetricand Interferometric SAR Data Processing[C]//Proceedings of 2008 IEEE Geoscience and Remote Sensing Symposium. Boston: IEEE, 2008: 471-474. |
| [21] | SIMARD M. 3D Global Vegetation Map[EB/OL]. 2011[2012-06-13]http://lidarradar.jpl.nasa.gov/. |
| [22] | ISOLA M, CLOUDE S R. Forest Height Mapping Using Space-borne Polarimetric SAR Interferometry[C]//Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium. Sydney: IEEE, 2001: 1095-1097. |