2. 国家海洋局 海底科学重点实验室, 浙江 杭州 310012;
3. 山东科技大学 测绘科学与工程学院,山东 青岛 266590;
4. 海岛(礁)测绘技术国家测绘地理信息局重点实验室,山东 青岛 266590
2.Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China;
3.Geomatics College, Shandong University of Science and Technology, Qingdao, 266590;
4.Key Laboratory of Surveying and Mapping Technology on Island and Reef, NASG, Qingdao, 266590
200海里以外大陆架划界是关系到国家海洋权益的重大问题,包括中国在内的许多沿海国均组建多专业联合工作组研究并编制划界案[1, 2, 3, 4]。大陆坡脚点(foot point of slope,FOS)是确定200海里以外大陆架系列界限的起点,是编制符合大陆架界限委员会(CLCS)要求的划界案所必备的核心界限点。《联合国海洋法公约》(简称《公约》)中关于200海里以外大陆架划界的第76条源于大西洋型大陆边缘[5],该类大陆边缘简单,但中国周边海域属于太平洋型大陆边缘,受板块汇聚作用影响,海底地形地貌异常复杂多变[6],导致FOS识别非常困难,同时也导致其他相关界限生成比较困难。
高精度水深数据和DDM(depth digital model)是确定FOS的基础,关于测深数据处理和DDM构建方面已取得较多的研究成果[7, 8, 9, 10, 11, 12, 13, 14, 15],但关于海洋划界方面的技术研究仍很少[5, 16, 17, 18]。文献[18]提出一种将水深转换为最大曲面(MCS,maximum curvature surface)的FOS识别方法,但该方法只适用于简单大陆边缘,相同的曲面可能对应完全不同的海底地形,因此存在误判FOS的风险。CARIS LOTS软件是一款商业划界软件,但该软件对于原始地形数据进行了滤波与平滑处理,有可能会改变FOS的精确位置,同时该软件的算法并未公开,难以进行技术交流,无法进行深化研究。
如何在不利条件下有效维护我国海洋权益,研究适用不同地形条件下的FOS自动识别方法,进而推广到特殊界限生成方法非常重要。针对该问题,本文提出一种基于地形、坡度、二阶导数及D-P剖面等综合分析的FOS自动识别方法,经试验获得了多重直接的FOS判识方法,并给出了详细的技术流程,最终实现了FOS的自动识别。
2 大陆坡脚点的定义及确定原则 2.1 FOS的基本定义准确理解大陆架及大陆边缘的含义是研究和识别大陆坡脚点的开始。1982年签署生效的《联合国海洋法公约》(1982年12月10日通过,1994年生效)第76条[5]规定:沿海国的大陆架包括其领海以外依其陆地领土的全部自然延伸,扩展到大陆边外缘的海底区域的海床和底土,如果从测算领海宽度的基线量起到大陆边的外缘的距离不到200海里,则扩展到200海里的距离;在大陆边从测算领海宽度的基线量起超过200海里的任何情形下,沿海国应以下列两种方式之一,划定大陆边的外缘:①按照第7款,以最外各定点为准划定界线,每一定点上沉积岩厚度至少为从该点至大陆坡脚最短距离的百分之一;②按照第7款,以离大陆坡脚的距离不超过60海里的各定点为准划定界线。第76条也是目前世界各沿海国提交200海里以外大陆架划界案,主张外大陆架的法律依据。大陆坡脚点是确定200海里以外大陆架的起点和核心界限点。
大陆边缘由陆架、陆坡和陆隆组成(图 1(a)),与《联合国海洋法公约》中论述的大陆架概念不同,此时的陆架仅是《联合国海洋法公约》中所定义的大陆架中的一部分。大陆边缘可划分为3种类型[5]:① 大西洋型;② 太平洋型;③ 转换型。大陆边缘外缘最好界定为地貌大陆的外部边缘,它通常精确解释为大陆坡的底部[8]。
《联合国海洋法公约》第76条关于200海里以外大陆架界限的确定主要来源于大西洋型大陆边缘,该类大陆边缘海底地貌类型清晰,完整的大陆边缘由陆架、陆坡、陆隆至海盆组成,大陆坡脚点位于陆坡下部到陆隆之间(图 1(a))。太平洋型大陆边缘受板块汇聚、俯冲挤压的影响,大陆边缘变得非常复杂,自陆向海分布陆架、弧后盆地、岛弧、弧前盆地、海沟至深海盆等多种地貌单元,此时,在弧后盆地两侧和海沟等多处出现大陆坡脚点(图 1(b))。作为中日韩划界焦点区的东海冲绳海槽就是典型的正在扩张的弧后盆地。

|
| 图 1 大陆边缘模型及大陆坡脚点理论位置(FOS:大陆坡脚点) Fig. 1 Continental shelf model and theoretical positions of FOS |
在没有相反证据的情况下,大陆坡脚点是大陆坡坡底梯度变化最大之点[5]。确定大陆架坡脚分为两大步骤:① 确定界定为大陆坡坡底的区域,也就是陆坡基部;② 确定大陆坡坡底坡度变化最大点的位置。
陆坡区海底地形复杂,确定大陆坡脚点前必须确定陆坡基部,也就是大陆坡脚点可能所在的区域。大陆坡脚点位于由大陆地壳向大洋地壳转换的地带(COB),陆坡基部的确定需要多方面的证据,其中海底地形地貌是最重要的证据之一,在空间上具备典型“陆架-陆坡-海盆”地形特征的区域才是确定大陆坡脚点的合理区域。
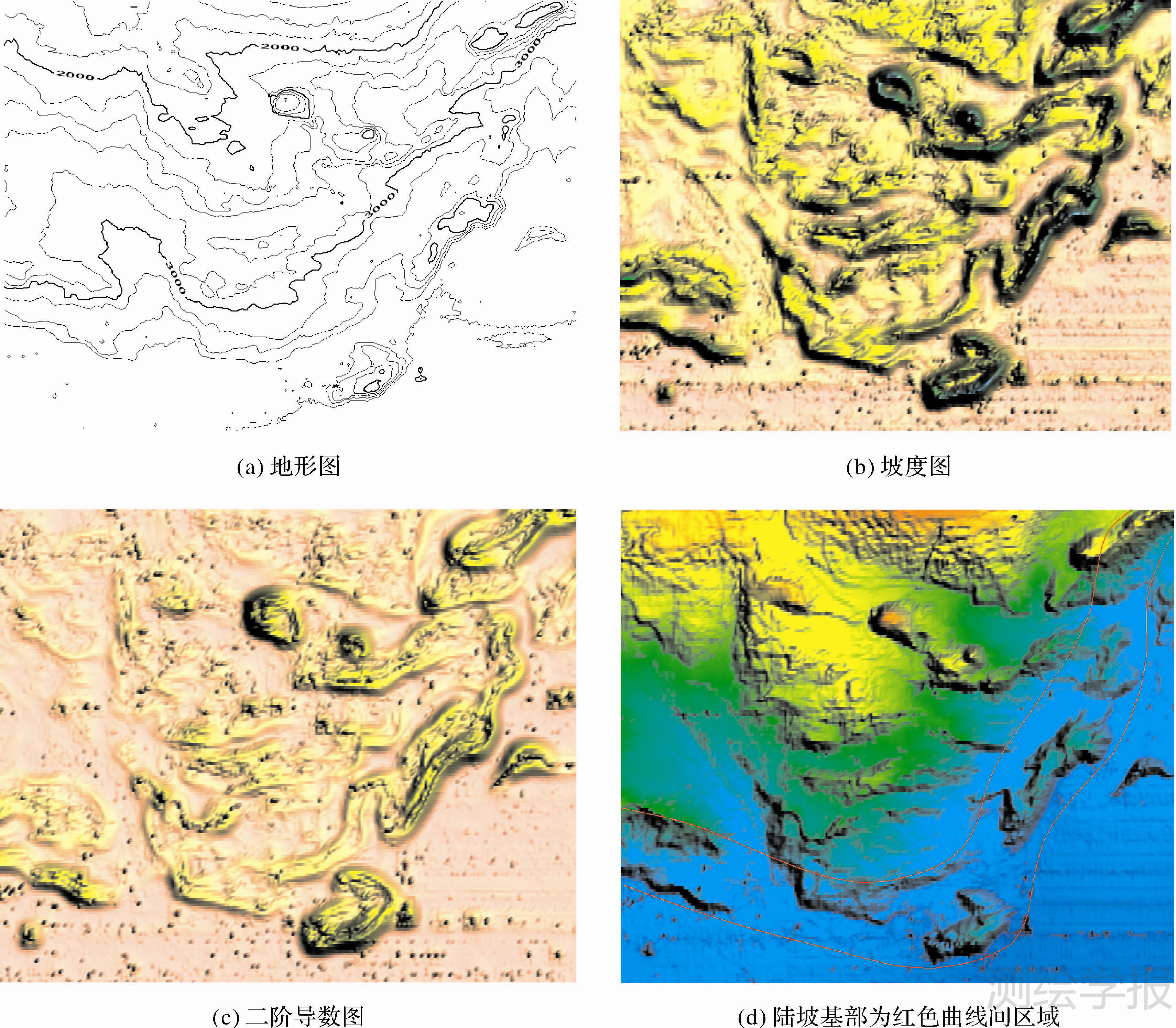
海底地形地貌往往是确定陆坡基部最直观的手段[19]。通过水深、地形、坡度和二阶导数的综合分析可以确定陆坡基部区域。图 2(a)展示的是一个大的斜坡地形区,水深自西北向东南逐渐加深,介于1500~3900m之间,从等深线的疏密程度看是一典型的陆坡至海盆过渡地形区。从坡度分析看(图 2(b)),该斜坡区地形崎岖不平,海底地形坡度变化较大,坡度总体特征与海底地形吻合,较大坡度区对应局部起伏地形。从二阶导数图分析看(图 2(c)),总体特征与坡度图类似,但趋势要平缓,同时二阶导数图中峰值对应的位置与坡度图中对应的位置是不同的,坡度峰值对应地形变化最大处,二阶导数极值对应地形梯度最大变化区,也就是大陆坡脚所在的区域。通过图层叠加,综合分析水深、地形、坡度和二阶导数等相关信息,可确定陆坡基部区域(图 2(d))。
|
| 图 2 陆坡基部的确定 Fig. 2 Determination of base region of slope |
准确、定量、可验证是对大陆坡脚点确定方法的基本要求。目前确定大陆坡脚点的方法是构建系列垂直陆坡走向的地形剖面线,从海底地形剖面变化来确定大陆坡脚点。但仅依赖地形剖面往往难以定量确定大陆坡脚点位置,还需要通过其他方法来综合分析以准确确定大陆坡脚点的位置。
大陆坡脚点被定义为地形梯度变化最大之点,其对应的是二阶导数极值点,而非坡度剖面的零值点,因此,大陆坡脚点往往并非地形剖面中的极值点。通过对比可发现,二阶导数极值点往往在地形极值点附近,但二者往往不重合。大陆坡脚点所处的地形剖面具有凸包性质(纵轴按照水深自浅向深的习惯显示),因此,曲线二阶导数值为极值点且为正值时是潜在的大陆坡脚点。但受小地形的影响,一条地形曲线的二阶导数极值点可能很多,因此,需要简化原始地形剖面。
一条典型的大陆边缘地形剖面由3段组成:平坦且水深较浅的陆架、倾斜且水深急剧变化的陆坡和平坦且水深较深的海盆。大陆坡脚点位于陆坡至海盆的转折处,水深较深,向陆坡方向的坡度较大,向海盆方向的坡度较小。对一条原始地形剖面而言,受局部小地形的影响,可能有很多点符合上述条件,因此,需要简化曲线,以消除局部地形的干扰。
可采用极值点和D-P算法二次拟合来简化原始地形剖面。D-P算法的一个显著优点是能保留曲线的最基本特征,但直接采用D-P算法拟合原始地形剖面也难以直接确定大陆坡脚点的位置,因为,符合D-P算法的点可能并非曲线的二阶导数极值点,也就是说D-P算法可能过滤了曲线的二阶导数极值点。因此,在进行D-P算法拟合前,应首先基于二阶导数极值点拟合原始剖面,然后在极值点剖面基础上再用D-P算法进行二次拟合,以保证所获取的点均为曲线二阶导数极值点,以免错判大陆坡脚点。
对于获取的D-P地形剖面进行二次求导,可以获取新的坡度剖面和二阶导数剖面。二次简化后的剖面仅保留曲线的最基本特征,已无小地形干扰,因此可以通过判断D-P剖面中每个点的水深值、坡度、二阶导数、凹凸特征,以及该点与邻近点上坡度、下坡度和水深值的相关性(连续性),以判断地形变化是否符合陆坡向海盆转折的典型特征(分段性),通过这几种参数可以准确判定大陆坡脚点在曲线中的位置。
3.2 地形剖面简化算法Douglas-Peucker算法(简称D-P算法)是由David Douglas和Thomas Peucker提出的一种曲线抽稀算法[20],可对曲线大量冗余点进行精简并保留曲线最基本特征。近年来,该算法在国内引起较多关注,已在图形压缩、冗余点删除和图像分割等方面得到应用[21, 22, 23]。简言之,根据曲线离散度给定一个初始距离偏差值D,将曲线首尾A和B点相连形成直线AB,并查询曲线所有拐点中距离直线AB最远的点(图 3(a)中点4)。如果该点与AB的距离d小于D,则删除曲线A—B之间所有拐点并返回,如图 3(b)中A—4段中1—3点经判断直接删除。若d大于D,则保留该点,并重新搜索首点至该点间距离最远的点,如图 3(c)中4—B段中9点。依此类推,直至搜索完曲线所有点并保留下特征点。

|
| 图 3 D-P算法流程示意,(a)、(b)和(c)示意算法筛选冗余点的过程 Fig. 3 Schematic diagram of D-P algorithm. (a)—(c) indicated the screening process of redundant points by algorithm |
目前实现该算法一般会用到递归函数,如果设计的数据结构体能记忆曲线前后查询点的全信息,在程序实现时无需递归函数。另一个值得关注的问题是初始距离偏差值D的大小将影响曲线简化的结果,该值太大将导致曲线太多的细节被删除,太小将保留较多的点而影响简化效果,程序能自动调节初始偏差值有利快速简化曲线。整体算法是D-P算法的突出优点,可保留曲线最大弯曲形态的点,也就是简化后的曲线形态不变,该特性与大陆坡脚点的求取是吻合的。识别大陆坡脚点也就是要寻找海底梯度变化最大之点,是地形剖面中的二阶导数极值点,在地形上位于陆坡至海盆的转折处。
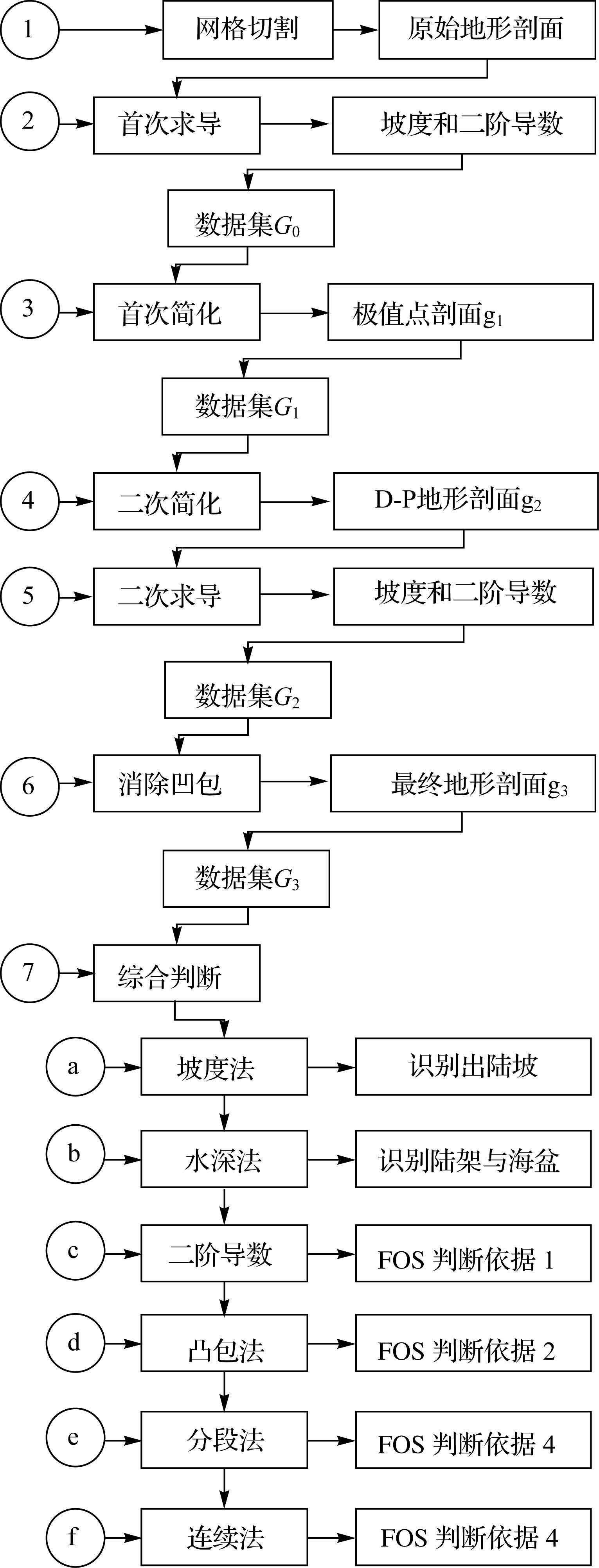
3.3 详细技术流程对于给定的数字水深网格模型(DDM),通过切割网格、首次求导、首次简化地形、二次简化地形、二次求导、消除凹包地形和综合判断7个步骤,以及6种判据实现了大陆坡脚点的自动识别(见图 4)。
|
| 图 4 大陆坡脚点识别的技术流程 Fig. 4 The identification technique-flow of FOS |
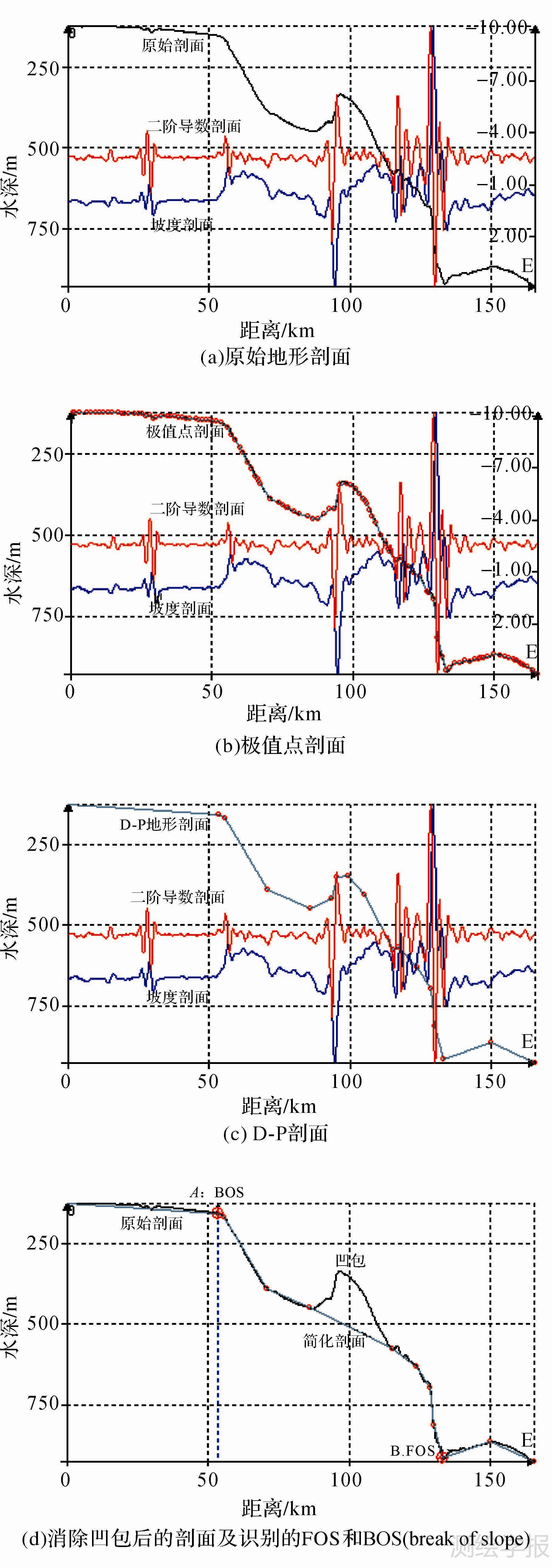
(1) 网格切割。使用直线切割海底地形网格模型,进行相交运算,获得原始地形剖面g0,该地形剖面要符合“陆架-陆坡-海盆”特征(见图 4和图 5(a))。
|
| 图 5 典型地形剖面及识别大陆坡脚点过程图 Fig. 5 Typical topographical profile and identification process of FOS |
(2) 首次求导。对地形剖面线进行首次求导,获得坡度剖面和二阶导数剖面。由距离、地形、坡度和二阶导数值共同组成数据集G0(见图 4和图 5(a))。
(3) 首次简化。仅保留二阶导数剖面极值点,并由极值点坐标和水深组成新的简化地形剖面g1,并形成新的数据点集G1,与原地形剖面相比,仅保留了符合二阶导数极值点特性的水深点(见图 4和图 5(b))。
(4) 二次简化。采用D-P算法[19],在极值点地形剖面g1中计算符合要求的数据点集G2,并形成新的地形剖面g2,该剖面是二次简化后的地形剖面,仅保留了少数符合要求的数据点(见图 4和图 5(c))。
(5) 二次求导。对g2所表达的地形剖面进行再次求导,形成新的坡度剖面和二阶导数剖面 (见图 4)。
(6) 消除凹包。采用二次循环,遍历地形剖面g2中所有点,消除符合凹包特征的点后形成新的点集G3,形成新的地形剖面g3、坡度剖面和二阶导数剖面(见图 4和图 5(d))。
(7) 综合判断。通过步骤(1)至步骤(6),获取简化后的综合剖面。经过2次简化、消除凹包后,地形剖面大幅简化,陆架和海盆地形平坦,陆坡地形坡度单一。可采用水深、坡度、二阶导数、凸包特征、连续性和分段性对步骤(6)形成的地形剖面g3进行查询和判断,识别并判断出大陆坡脚点(见图 4)。
(a) 坡度法。对剖面点的坡度值进行分类,分别获取陆架与海盆平均坡度,以及陆坡区平均坡度,按照坡度差异识别出陆坡区。
(b) 水深法。对剖面点进行深度分类,获得陆架平均水深值和海盆平均水深值,从而识别出陆架和海盆。
(c) 二阶导数。大陆坡脚点FOS是陆坡至海盆海底坡度最大变化之点,也就是二阶导数极值点。
(d) 凸包特性。大陆坡脚点FOS位于陆坡至海盆转折处,因此在地形上具有凸包特征,也就是二阶导数值为正值的数据点。
(e) 分段性法。大陆坡脚点相邻的前后点分别为陆坡和海盆,通过陆坡和海盆坡度差异的分段性可初步判断出大陆坡脚点FOS。
(f) 连续性法。按照坡度相近规则,剖面点向首点和尾点生长,并记录每个点向剖面首、尾点的生长距离,生长距离最远者为大陆坡脚点FOS。
综合运用步骤(a)至(f),同时满足(c)—(f)条件的数据点为大陆坡脚点FOS。
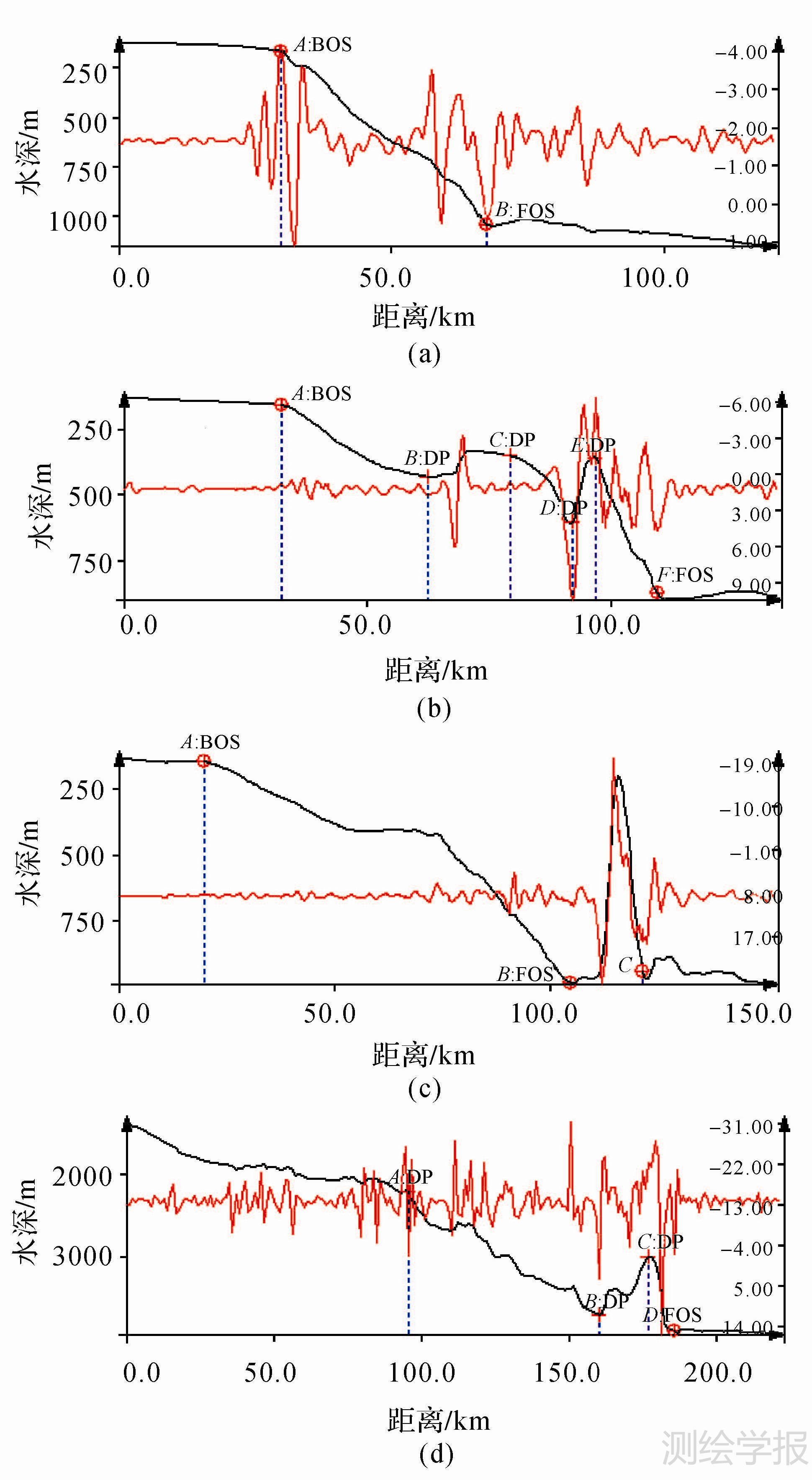
3.4 典型剖面中大陆坡脚点的识别在实际应用中,FOS的判断易受多种因素的影响,在程序设计时要考虑多种复杂情况。图 6(a)—(d)展示了4种不同类型的典型大陆边缘地形剖面,图 6(a)—(c)位于弧后盆地,图 6(d)位于扩张性大陆边缘。图 6(a)为标准的大陆边缘地形剖面,由“陆架-陆坡-海盆”组成,其特征容易判断,A点是陆架和陆坡的分界点,B点是陆坡至海盆的分界点,也就是FOS。图 6(b)虽然也能识别出“陆架-陆坡-海盆”地形特征,但陆坡异常复杂,受海底峡谷切割和构造运动影响,陆坡区显得支离破碎,局部分布凸起和下凹地形,因此,FOS识别易受局部地形的影响,图中B点和D点易被程序误判为FOS,此时要通过地形剖面的整体形态来判断,通过消除凹包可避免这些局部地形的干扰。图 6(c)展示了海盆边缘海山对FOS判断的影响,如果仅考虑FOS处地形的转折特征,图中C点易被误判为FOS,因为该点坡度和二阶导数均处于高值区,也要从剖面的整体特征来判断,通过曲线的分段性和连续性特征可排除干扰。图 6(d)展示了在宽陆坡背景下叠加海丘的情形,在陆坡的外缘叠加一低矮的海丘,阻断了陆坡向海盆的自然延伸,B点易被误判为FOS,但通过整条剖面的分析,D点是合理的FOS,自D点向海盆方向海底地形由陡峭变平坦,符合陆坡向海盆转折的特征,此时也可通过消除凹包地形排除局部地形对FOS判识的干扰。对地形剖面整体特征的自动识别是准确判断FOS的基础,需要程序自动识别剖面中每个数据点的特征和类别。
|
| 图 6 典型剖面分析(黑色曲线为地形,红色曲线为二阶导数) Fig. 6 Analysis of typical profiles(black curve: the terrain; red curve: second derivative of the terrain) |
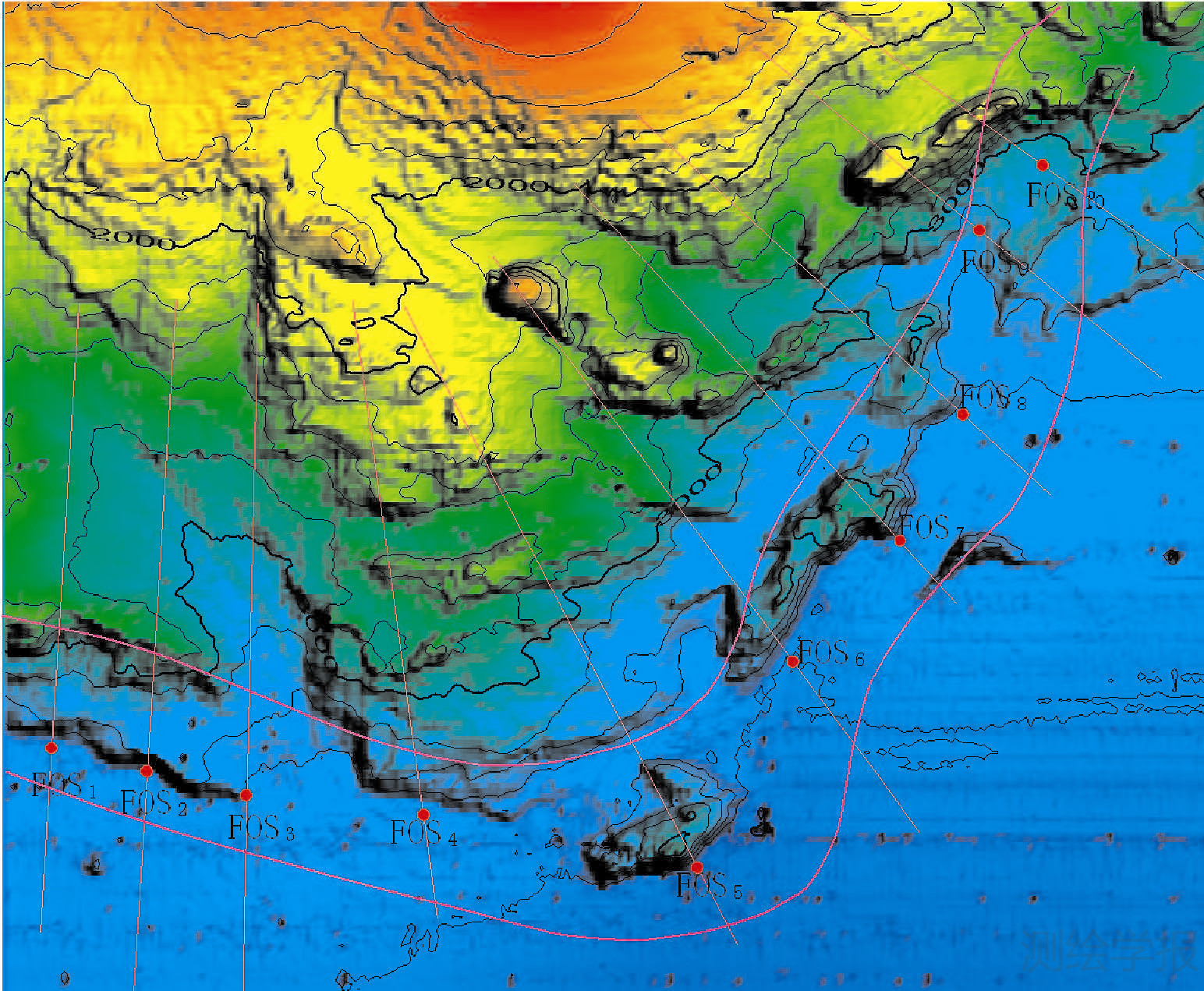
根据《联合国海洋法公约》第76条和大陆架划界委员会相关技术准则要求,分两步确定大陆坡脚点。首先,基于多波束水深数据形成某大陆架区200m分辨率的DDM(图 7),并在此基础上形成了坡度(图 3(b))和二阶导数网格(图 3(c)),通过3种网格的叠加分析,确定了陆坡基部区域(图 3(d))。其次,自NW-SE走向沿垂直大陆坡方向构建了10条原始地形剖面(图 7),采用3节所述之方法,使用地形、坡度、二阶导数和D-P剖面相结合的自动分析方法,确定了该大陆架10个大陆坡脚点所在的位置(图 7中FOS1—FOS10)。这些大陆坡脚点均位于陆坡基部区域,且位于陆坡下部至海盆的转折处,是合理的大陆坡脚点。为验证程序的有效性,采用相同的数据和相同的地形剖面,用CARIS LOTS软件对计算结果进行了验证。
在应用实例(图 7)中还使用不同分辨率的DDM对算法进行了检验,包括200m、400m、600m和800m的多种分辨率的DDM,所设计的算法体现了良好的抗差性能,在DDM不影响海底地形刻画的情况下,能准确识别出不同分辨率DDM情况下的FOS。
|
| 图 7 确定大陆坡脚点实例 Fig. 7 An example of determination of FOS |
(1) 阐述了《联合国海洋法公约》关于大陆架的发展历史,以及大陆架含义的异同,定性确定了不同类型大陆边缘中大陆坡脚点的空间位置。
(2) 提出通过地形图、坡度图和二阶导数图综合叠加分析的方法,确定了陆坡基部,为准确寻找大陆坡脚点确定了区间位置。
(3) 建立了大陆坡脚点自动识别技术方法与详细流程。基于地形、坡度和二阶导数剖面,获取了二阶导数极值点和D-P算法二次拟合剖面,进行原始剖面和D-P剖面的二次求导。通过七大步骤获取了4套逐渐简明的剖面数据集,并通过剖面点的水深、坡度与二阶导数值,以及曲线的凹凸性、分段性和连续性等多特征综合分析方法,实现了大陆坡脚点的自动识别。
(4) 底层编程实现了大陆坡脚点的自动识别算法,并用实测数据对程序进行了有效性验证。
| [1] | Submission by the Russian Federation. Outer Limits of the Continental Shelf beyond 200 Nautical Miles from the Baselines: Submissions to the Commission [EB/OL]. [2012-11-10]. http://www.un.org/ depts/los/clcs_new/submissions_files/rus01/rus_page1_Arctic.pdf. |
| [2] | Submission by the People's Republic of China. Outer Limits of the Continental Shelf beyond 200 Nautical Miles from the Baselines [EB/OL]. [2012-11-10]. http://www.un.org/depts/los/ clcs_new/ submissions_files/chn63_12/executive%20summary_ch.pdf. |
| [3] | Submission by the Republic of Korea. Outer Limits of the Continental Shelf beyond 200 Nautical Miles from the Baselines: Submissions to the Commission [EB/OL]. [2012-11-10].http://www.un.org/depts/los/clcs_new/submissions_files/preliminary/kor_2009preliminaryinformation.pdf. |
| [4] | Submission by Japan. Outer Limits of the Continental Shelf beyond 200 Nautical Miles from the Baselines: Submissions to the Commission[EB/OL]. [2012-11-10].http://www.un.org/depts/ los/clcs_new/submissions_files/jpn08/jpn_execsummary.pdf. |
| [5] | PETER J C, CARLETON C. Continental Shelf Limits: The Scientific and Legal Interface[M]. Oxford: Oxford University Press, 2000. |
| [6] | LIU Guangding. Geological-geophysical Features of China Seas and Their Adjacent Regions [M]. Beijing: Science Press, 1992. (刘光鼎. 中国海区及邻域地质地球物理特征[M]. 北京: 科学出版社, 1992.) |
| [7] | YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The Methods of High Quality Post Processing for Shallow Multibeam Data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 444-457. (阳凡林, 李家彪, 吴自银, 等. 浅水多波束勘测数据精细处理方法[J]. 测绘学报, 2008, 37(4): 444-457.) |
| [8] | YANG Fanlin , LI Jiabiao, WU Ziyin, et al. The Methods of Removing Instantaneous Attitude Errors for Multibeam Bathymetry Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 450-456. (阳凡林, 李家彪, 吴自银, 等. 多波束测深瞬时姿态误差的改正方法[J]. 测绘学报, 2009, 38(5): 450-456.) |
| [9] | ZHANG Hongmei, ZHAO Jianhu. Quality Control of GPS Height in Precise MBS Measurement[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 22-27. (张红梅, 赵建虎.精密多波束测量中GPS高程误差的综合修正法[J]. 测绘学报, 2009, 38(1): 22-27.) |
| [10] | HUANG Xianyuan, ZHAI Guojun, SUI Lifen, et al. The Influence of Optimized TRA in Samples on Elimination of Sounding Outliers in the LS-SVM Arithmetic[J]. Acta Geodaetica et Cartographica Sinica, 2001, 40(1): 22-27. (黄贤源, 翟国君, 隋立芬, 等. LS-SVM算法中优化训练样本对测深异常值剔除的影响[J]. 测绘学报, 2001, 40(1): 22-27.) |
| [11] | WANG Haidong, CHAI Hongzhou, WANG Min. Multibeam Bathymetry Fitting Based on Robust Kriging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 238-248. (王海栋, 柴洪洲, 王敏. 多波束测深数据的抗差Kriging拟合[J]. 测绘学报, 2011, 40(2): 238-248.) |
| [12] | ZHANG Lihua, JIA Shuaidong, WU Chao, et al. A Method for Interpolating Digital Depth Model Considering Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 359-365. (张立华, 贾帅东, 吴超, 等. 顾及不确定度的数字水深模型内插方法[J]. 测绘学报, 2011, 40(3): 359-365.) |
| [13] | ZHANG Lihua,JIA Shuaidong,YUAN Jiansheng, et al. A Method for Controlling Shoal-bias Based on Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 184-190. (张立华, 贾帅东, 元建胜, 等. 一种基于不确定度的水深控浅方法[J]. 测绘学报, 2012, 41(2): 184-190.) |
| [14] | JIA Shuaidong, ZHANG Lihua,SONG Guoda, et al. A Method for Constructing an Adaptive Grid Digital Depth Model Based on Mean Vertical Uncertainty of Area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 454-460. (贾帅东, 张立华, 宋国大, 等. 基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454-460.) |
| [15] | HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. Data Fusion Technique for Single Beam and Multibeam Echo Soundings[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 299-303. (黄谟涛, 翟国君, 欧阳永忠, 等. 多波束与单波束测深数据的融合处理技术[J]. 测绘学报, 2001, 30(4): 299-303.) |
| [16] | LIU Zhijun, LIU Jin, JIN Jiye. Study on Automatic Drawing of Foot Line of Extended Continental Slope[J]. Computer Engineering and Applications, 2007, 43(31): 240-241. (刘志军,刘金,金继业. 外大陆架坡脚线自动绘制研究[J]. 计算机工程与应用, 2007, 43(31): 240-241.) |
| [17] | PENG Rencan, WANG Jiayao. A Research on Creating Buffer on the Earth Ellipsoid[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 270-273. (彭认灿, 王家耀. 基于地球椭球体的缓冲区构建技术研究[J]. 测绘学报, 2002, 31(3): 270-273.) |
| [18] | OU Z Q, VANCˇEK P. Automatic Tracing of the Foot of the Continental Slope[J]. Marine Geodesy, 1996, 19(2): 181-195. |
| [19] | HEDBERG H D. Ocean Boundaries and Petroleum Resources[J]. Science, 1976, 191(4231): 1009-1018. |
| [20] | DOUGLAS D, PEUCKER T. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973, 10(2): 112-122. |
| [21] | ZHAO Yongqing, XIE Chuanjie, QIAO Yuliang, et al. Douglas-Peucker Compressing Algorithm about Extreme Points[J]. Software Guide, 2008, 11(7): 60-62. (赵永清,谢传节,乔玉良,等. 基于最值点的道格拉斯-普克压缩算法[J]. 软件导报, 2008, 11(7): 60-62.) |
| [22] | PENG Rencan, DONG Jian, ZHENG Yidong, et al. The Efficiency Comparison of Methods between Perpendicular Distance and Douglas-Peucker in Deleting Redundant Vertexes [J]. Bulletin of Surveying and Mapping, 2010(3): 66-71. (彭认灿, 董 箭, 郑义东, 等. 垂距法与道格拉斯-普克法删除冗余顶点效率的比较[J]. 测绘通报, 2010(3): 66-71.) |
| [23] | SUN Chengbo,LI Yikun,ZHANG Zhihua. The Preliminary Study of Image Segmentation Based on Douglas-Peucker Algorithm[J]. Geomatics & Spatial Information Technology, 2012, 35(5): 33-38. (孙承勃,李轶鲲,张志华. 基于道格拉斯-普克算法的图像分割初探[J]. 测绘与空间地理信息, 2012, 35(5): 33-38.) |



