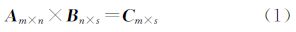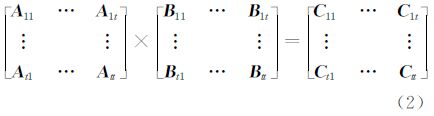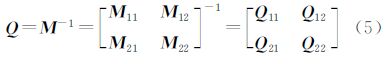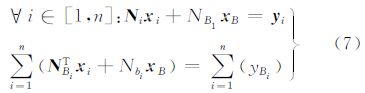1 引 言
随着全球导航卫星系统(global navigation satellite system,GNSS)在越来越多的学科和领域发挥愈来愈巨大的作用，许多国家和地区广泛建立各种连续运行参考站网络(continuously operating reference system,CORS)。成百上千个参考站的实时观测使得GNSS的数据量成几何倍数增长，相关的大型网络GNSS数据处理受到越来越多的重视，特别是大型网络实时数据快速解算[1]。为了实现大型GNSS网平差数据的高效处理，国内外研究机构和研究人员从降低数据处理算法复杂度等角度进行了广泛的关注和研究[2, 3, 4, 5]，文献[2]提出一种新的参数消去方法解决GNSS数据处理过程中面临的大量模糊度参数解算，文献[3, 4]根据“不动点理论”提出Ambizap算法用于基于PPP的GPS网解算，文献[5]利用解算约化代替求逆约化，提出一种分区平差快速解算新算法。另一方面，随着计算机硬件平台的高速发展，多核CPU结合众核GPU已成为当前通用计算机体系架构的主流，使得普通PC拥有了“超级计算”的性能，相应的多核并行计算技术及其应用引起了越来越多的重视，而传统的GNSS数据处理程序多是针对单处理器体系架构编写的，数据处理的硬件平台性能利用效率很低。对现有的测量数据处理软件代码并行化或者独立开发并行软件系统成为解决大规模测量数据处理的新方法。如国际大地测量协会(International Association of Geodesy，IAG)的第1工作小组负责的Dancer项目利用分布式并行计算技术开发的Dancer系统，实现了参考框架并行计算[6]。瑞士伯尔尼大学推出的GNSS数据处理软件Bernese5.0版本，采用多线程并行计算技术处理GNSS数据，并支持在不同计算机之间的远程调用和并行处理[7]。
随着更高抽象层次的基于“任务”的并行开发的扩展[8]，并行计算程序的开发难度逐步降低，并行计算技术从服务器、工作站等应用程序走到了传统的桌面应用程序。实现GNSS网平差数据处理的多核并行计算既充分发挥多核体系带来的性能优势，又极大提高了GNSS数据处理效率。本文分析GNSS网平差数据处理涉及的数值计算任务，利用矩阵分块的理论与方法研究相关并行计算的关键算法，通过多个算例实现矩阵分块方法在多核环境下GNSS网平差数据并行处理的应用。
2 GNSS数据处理并行分析GNSS数据处理过程中，由于卫星、测站等数目的增加，待估参数更加庞大复杂，所需的计算能力不断提高，多时段和多测站的大型GNSS网平差数据处理带来的计算瓶颈成为当前亟需解决的问题[2, 3, 6]。由于时空的分布性，多时段或者多测站的观测数据进行数据预处理、设计矩阵计算等步骤中具有较多良好的并行过程，在多核并行计算环境下，建立多个线程并行处理即能充分利用硬件资源和提高计算效率，无须设计复杂的并行算法。而GNSS网平差数据处理过程中的热点数值计算任务，如高维矩阵乘法、法方程求逆则是并行研究的重点。由于多核CPU硬件结构属于共享存储的对称处理器，独立开发共享存储编程模型的并行数据处理系统，关键是对算法的并行设计和任务分解设计[9, 10]。对于时序观测的GNSS网平差数据，采用滤波或者序贯的处理方法有效的降低了矩阵阶数，但却不适合并行处理。以下从整体平差的角度研究相关的并行算法，采用矩阵分块的理论与方法[11, 12, 13]，重新设计并行计算算法，将分解的计算任务分配给多核并行完成，能有效降低算法的开发难度，而且具有较好的扩展性和移植性。
2.1 矩阵的分块运算 2.1.1 矩阵分块乘法对于矩阵相乘
假设有t个处理器，则将每个矩阵均匀分为t×t块
式中，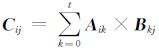
。
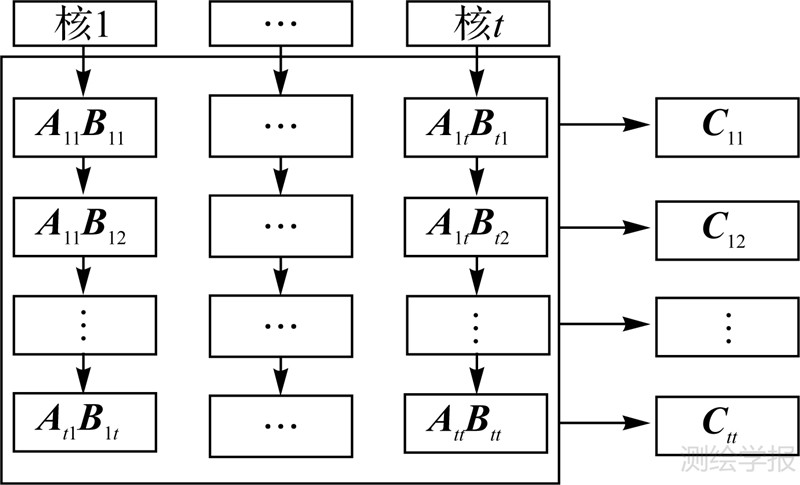
如图 1，将矩阵A与B分块后，每个核能够均匀得到相应的计算任务，通过索引标记完成各自的块矩阵相乘，通过累加得到结果块矩阵，经过t×t次运算后合并即可得到结果矩阵，保证了多核CPU性能的有效利用与负载平衡。
|
| 图 1 矩阵分块并行相乘示意图 Fig. 1 Parallel multiplication of a block matrix |
GNSS数据处理中涉及的高维系数矩阵的运算，采用上述分块并行处理方法，既可降低存储对内存的要求，也有效提高了计算效率。矩阵分块过程可根据矩阵规模大小自定义分块数目或者进行二次分块。
2.1.2 法矩阵的Cholesky分块分解在法方程Ax=b求解中，法方法中的法矩阵A一般是n×n阶对称正定矩阵。对法方程的求解，很多文献均采用稳定性较好的Cholesky分解法[5, 14]，通过对法矩阵A进行Cholesky分解，然后再回代求解x
式中，L是下三角矩阵。采用分块方法，假定对法矩阵分成4块，则
式中，A11=L11L11T、A12=L11L21T、A13=L11L31T、A14=L11L41T、A22=L21L21T+L22L22T、A23=L21L31T+L22L32T、
A24=L21L41T+L22L42T、A33=L31L31T+L32L32T+L33L33T、A34=L31L41T+L32L42T+L33L43T、A44=L41L41T+L42L42T+L43L43T+L44L44T。
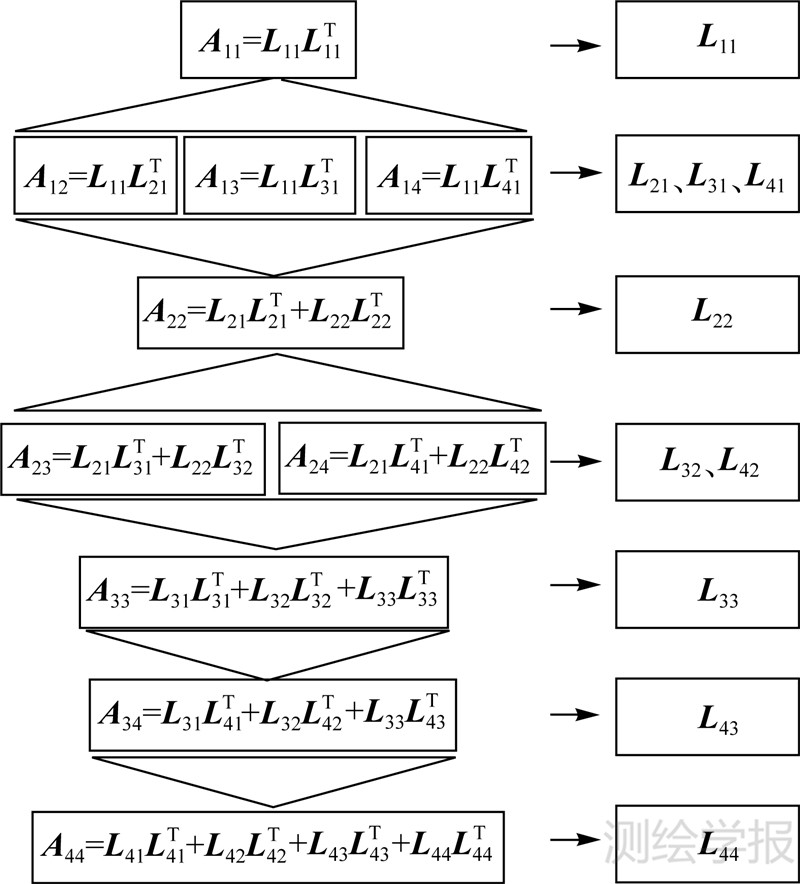
对角线上的块矩阵Aii仍为对称正定矩阵，进行矩阵的Cholesky分解求解Lii。非对角线上块矩阵Lij(i≠j)利用对角线矩阵分解产生的下三角矩阵Lii与Aij(i≠j)进行求解。采用分块分解有效降低了矩阵分解维数，其非对角线上互不相关的计算过程可并行计算。较粗粒度的计算流程如图 2。
|
| 图 2 分块矩阵Cholesky并行分解示意图 Fig. 2 Parallel Cholesky decomposition of a block matrix |
理论上每一步的矩阵相乘或者矩阵相加均可实现并行计算，算法执行过程中，每一步可根据矩阵的大小判断是否进行更细粒度的分块运算。通常，细粒度的并行计算流程的实现更复杂，当矩阵运算规模较小时，多核环境下并行计算效率反而低于直接分解的效率。
2.1.3 法矩阵的分块求逆不论是法方程求解，还是精度评定过程中，往往涉及计算比较耗时的对称正定矩阵求逆，除了采用上节矩阵分块分解法求逆，一般也可采用分块降阶求逆[15, 16]
式中，Q11=M11－M12M22－1M21－1、Q22=M22－M21M11－1M12－1、Q12=M11－1(－M12Q22)、Q21=M22－1(－M21Q11)。采用分层分块的方法，针对n个计算节点，需经过m=logn2 层分解，其中每层分解时将所有对角线上的块矩阵再次分成2×2块矩阵。当n=8时具有如图 3的结构。
|
| 图 3 矩阵分层分块示意图 Fig. 3 Layered decomposition of a matrix |
针对矩阵M求逆，假设现有4个计算节点，则分为2层，分解步骤如下：
第1层，将M分解2×2块矩阵，则对应逆阵Q也为2×2矩阵，表达式如式(5)。
第2层，将对角线上的矩阵M11和M22分别分解为2×2块矩阵
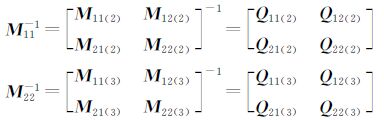
式中
Q11(2)=M11(2)－M12(2)M22(2)－1M21(2)－1
Q11(3)=M11(3)－M12(3)M22(3)－1M21(3)－1
Q22(2)=M22(2)－M21(2)M11(2)－1M12(2)－1
Q22(3)=M22(3)－M21(3)M11(3)－1M12(3)－1
Q12(2)=M11(2)－1(－M12(2)Q22(2))
Q12(3)=M11(3)－1(－M12(3)Q22(3))
Q21(2)=M22(2)－1(－M21(2)Q11(2))
Q21(3)=M22(3)－1(－M21(3)Q11(3))
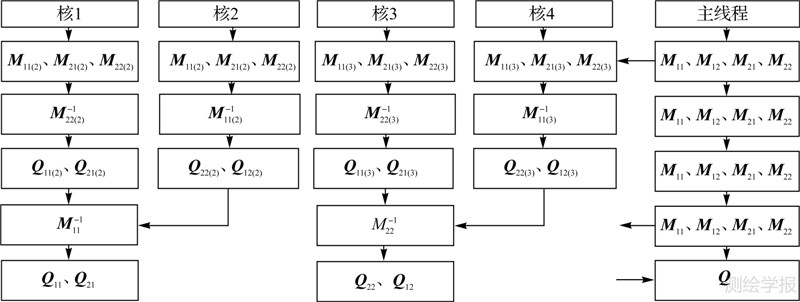
则4个计算节点首先同时求M11(2) 、M11(3) 、M22(2) 、M22(3) 的逆，再根据所在的2×2阶块矩阵并行求得逆矩阵的对角块矩阵Q11(2) 、Q22(2) 、Q11(3) 、Q22(3) ，再并行求得Q21(2) 、Q12(2) 、Q21(3) 、Q12(3)，通过块矩阵的融合得到M11－1、M22－1，根据第1层分解得到的块矩阵并行得到Q11 、Q22 ，进而并行求得Q12 、Q21 ，再通过块融合得到M的逆矩阵Q。
相应的并行计算流程如图 4。
|
| 图 4 分块矩阵并行求逆示意图 Fig. 4 Parallel inversion of a block matrix |
采用分块的方法进行矩阵的运算，算法粒度可根据数据计算任务规模与实际硬件平台进行调整，矩阵的划分即可根据核数目进行划分，也可根据自定义块矩阵大小划分。一般采用粗粒度算法减少系统开销的方式既能提高代码的执行效率，而且降低并行系统的开发难度，实践起来简单易行，移植性好。
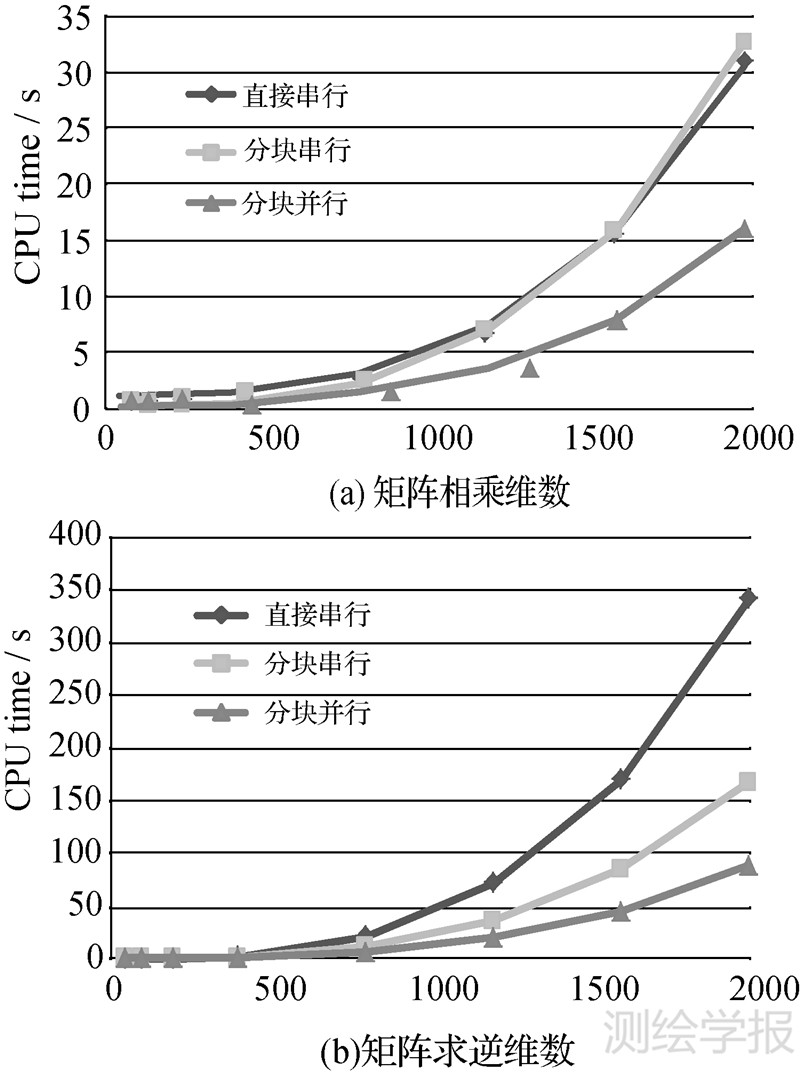
为了验证分块方法的有效性，针对C=ATA和M=C－1，设计不同阶数的方阵A，求取C和M。测试用的PC普通基本配置为Intel(R) Core(TM) i3-2100处理器，主频3.10 GHz，内存4 GB，操作系统为Windows XP Professional，物理核数为4个。根据核数均匀分块，编写常规串行、分块串行和分块并行的矩阵运算程序，得到如图 5的运行时间。
|
| 图 5 不同阶数的矩阵乘法和求逆运算时间比较 Fig. 5 Runtime of the multiplication and inversion of different definite matrix |
为了描述多核并行计算的性能，一般采用加速比指标进行度量。加速比定义[8, 17, 18]为
式中，n表示处理器个数；T1是改进前整个任务的执行时间；Tn是改进后n个处理器并行执行时间。可见当n=4时，理论最高加速比为4，但由于任务执行存在不可避免的串行部分和其他系统开销，试验加速比很难达到理论值。由图 5(a)知，采用分块并行方法改进后的矩阵乘法的加速比基本达到2.0，相当于比分块串行运算提高了2倍，由图 5(b)知，采用分块并行方法改进后的矩阵求逆的加速比接近为1.6，相当于比分块串行运算提高了1.6倍。分析试验结果可以得出：① 由于矩阵分块过程需要一定开销，总的矩阵相乘计算量没有改变，所以矩阵分块串行相乘时间比矩阵直接串行相乘花费较多的时间，而由于矩阵分块求逆降低了求逆规模，采用矩阵分块串行求逆比直接串行求逆更快，但通过分块并行化矩阵相乘或求逆后，相应的计算效率比串行运算都得到较大提高；② 不考虑硬件平台的限制，计算任务规模越大，并行计算技术的优势越明显；③ 当计算任务较小时，由于并行机制的建立也需要开销，采用并行计算技术并不能带来效率的提高。总之，采用矩阵分块的方法，根据适合的分解粒度进行任务均匀分配，减少了线程之间的排队与竞争，降低了通信等系统开销，代码并行执行效率得到提高。未来的GNSS数据处理软件，应能根据计算任务的规模自主选择并行处理还是串行处理。
3 应用与分析时序观测的GNSS网平差数据处理过程中，设计的系数矩阵的整体表现形式一般有以下两种形式[19]：第1种形式是参数始终不变，观测值不断增加，对应的系数矩阵如图 6(a)；第2种形式是对应的参数部分不变，称为全局参数，对应的系数矩阵如图 6(b)。以下通过几个算例，根据矩阵分块运算的并行策略，从整体平差的并行处理对现有的GNSS数据处理程序进行并行设计，验证多核并行计算环境下矩阵分块方法在GNSS数据处理中的有效性。
|
| 图 6 两种不同形式的系数矩阵 Fig. 6 Two different forms coefficient matrix |
本文的算例均利用.NET4.0框架下的并行扩展(parallel extensions)实现。2010年，微软发布.NET4.0时推出的以并行任务库(TPL: task parallel library)为核心的parallel extensions从更高的抽象层次上构建并行计算基础框架，大大降低了.NET平台上并行计算程序的开发难度[20]。所采用的硬件平台依然为四核处理器的台式计算机。开发语言采用VS2010的C#。
3.1 算例1：多期同步网的并行计算
算例模拟CORS站组成的同步网经过基线解算后得到的独立基线向量和协方差矩阵，网中总点数1000个，其中已知点10个，未知点990个，未知参数仅考虑三维坐标参数，对连续8 d的基线观测量，采用参数平差模型，以基线为观测值编写网平差程序[21]。由于网中参数不变，误差方程系数矩阵形具有如图 6(a)的特征，则通过并行累加求取法方程系数N=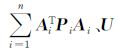
=
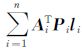。其中，每天的已知基线向量信息保存为一个向量组文件VectorsFile[i](i=0,1，…,7)，坐标信息保存为一个公共文件CoordFile。在.NET4平台下利用TPL对8个时段进行并行循环调用网平差程序，通过并行读取VectorsFile[i]文件建立误差方程，得到Ai、Pi、Li，进而将每个时段的法方程系数AiTPiAi和AiTPiLi并行累加到公共变量N和U上，最后利用分块并行求逆程序对法矩阵N求逆，利用分块并行乘法程序求N－1和向量U的乘积。
由于网型较大，误差方程系数矩阵Ai采用稀疏矩阵表示，法矩阵N大小为2970×2970阶。经过多次试验，法方程系数累加的串行计算时间4.16 s，经过并行化后计算时间仅需1.13 s，加速比达到了3.68，相当于比单核串行计算时间提高了3.68倍。
3.2 算例2：大型GNSS网平差的高斯消去并行计算对大型GNSS网进行平差计算，一般采用分区(组)平差模型，设公共的全局参数为xB，每个分区的区内参数为xi(i=1,2,…,n；n表示分区的个数)，分区平差模型的误差方程系数矩阵具有如图 5(b)的特征，图中Ai和Bi是各个分区对应xi和xB的系数矩阵，设对应的误差方程常数项为Li，权矩阵为Pi，则法方程组形式如下
式中，Ni=AiTPiAi；NBi=AiTPiBi，AiTPili=yi；Nbi=BiTPiBi；BiTPiLi=yBi。则由误差方程得到的法方程的法矩阵具有如图 7(a)的特点，其中NB=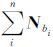
。大型GNSS网中待估参数较多，从数值并行计算的角度实现大网的并行平差，重点是大型法方程的并行解算。对具有图 7(a)特点的法矩阵，通常法方程首先通过类似高斯消去法消去下三角的块矩阵，得到如图 7(b)的结构，其中NB* =
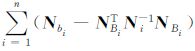，对应的常数项变成U*B =
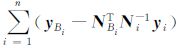。利用NB*和UB*求得公共参数xB，再回代求解区内参数xi。由于各区之间相互独立，各区的计算过程可并行实现，如消去过程、回代求解区内参数xi等。
|
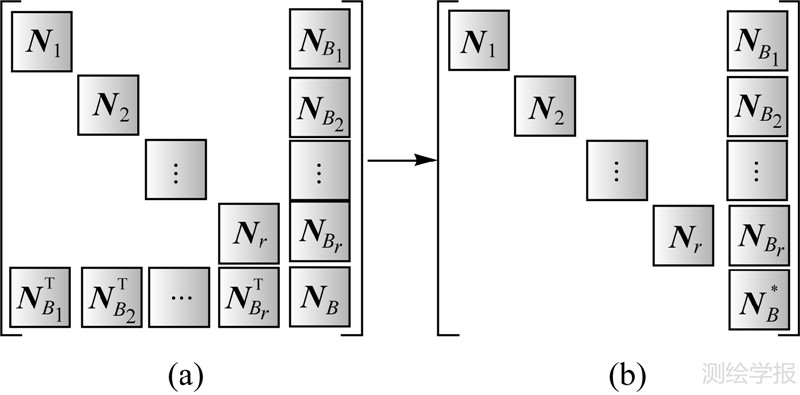
| 图 7 法矩阵高斯消去块矩阵示意图 Fig. 7 Normal matrix solved by Gauss elimination |
算例模拟利用基线向量进行大型GNSS网平差，观测方程8400个，未知参数2000个，则整体误差方程系数矩阵为8400×2000阶，根据计算机核数均匀分为4个区，其中全局公共参数为400个，每个分区内部参数为400，每个区对应xi和xB的系数矩阵Ai和Bi大小为2100×400阶，权矩阵Pi取单位阵。为了得到NB* 和UB*，设计子计算任务SubCalculate，完成Ai、Bi、Li、Pi计算得到(Nbi－NBiTNi－1NBi)和(yBi－NBiTNi－1yi)的任务，在.NET4平台下利用LTP以任务的形式多核并行调用SubCalculate，然后并行累加(Nbi－NBiTNi－1NBi)和(yBi－NBiTNi－1yi)得到NB*和UB*，利用Cholesky分块并行分解NB*，然后再分块并行解算得到全局参数xB，利用得到的xB再多核并行解算xi。由于稀疏矩阵相乘和矩阵分解后不一定还是稀疏矩阵，这里采用稠密矩阵表示NB*。
经过多次试验，该模拟的大网利用高斯消去法的串行计算时间为22.21 s，经过对其中的可并行化过程进行上述多核并行化设计后，计算时间约为10.19 s，加速比为2.18。
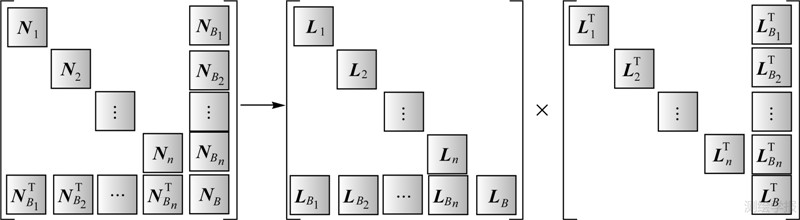
3.3 算例3：大型GNSS网平差的Cholesky分解并行计算通过对算例2分析，采用消去法消去块矩阵的求解过程中，矩阵消去过程占用时间较大。针对法矩阵的结构特点，本文采用Cholesky分解对法矩阵直接进行矩阵分解，将图 7(a)的法矩阵分解为下三角阵和上三角阵，然后求解参数xi和xB。矩阵分解结构示意图如图 8，对角线上的Ni对称正定，分别进行Cholesky分解Ni=LiLiT，然后通过NBi和Li求解LBiT，最后再求得LB。
|
| 图 8 法矩阵Cholesky分解示意图 Fig. 8 Normal matrix solved by Cholesky decomposition |
其中，Ni=LiLiT，NBi=LiLBiT，NB－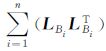
=LBLBT。
采用算例2的数据，设计新的子计算任务NewSubCalculate，完成由Ai、Bi、Li、Pi计算得到Li、LBi、yi、NBi和yBi，同样在.NET4平台下利用LTP以任务的形式多核并行调用NewSubCalculate，然后并行累加Nbi和yBi得到NB和yB，利用LBi和NB求得LB，根据图(8)右侧的下三角矩阵，利用Li、yi多核并行求得一组新的y′i，利用LBi、LB、y′i和yB得到新的y′B，然后利用LB的转置求得xB，通过xB和LBiT与LiT多核并行求得xi。
经过多次试验，该算法的串行计算时间为17.11 s，并行化后的计算时间约为8.02 s，并行加速比为2.13。与算例2比较，算例3的并行计算时间比之提高了20%。可见，针对相同硬件平台下同一平差计算问题，采用不同的并行算法得到不同的计算效率，设计高效的并行算法是GNSS网平差数据高效处理的一个关键问题。
4 总 结多核环境下的GNSS数据并行处理，既能充分发挥多核体系架构带来的计算性能优势，又能有效提升计算效率。随着并行系统开发难度的降低，设计高效的并行算法，实现GNSS数据任务的有效、合理并行分解是关键的难点。采用矩阵分块的方法研究GNSS数据并行处理为大型GNSS网平差数据处理提供一种有效的实现途径。
伴随当今信息与网络通信技术的飞速发展，将单机多核并行计算环境扩展到利用现有的多台多核通用计算机构成的分布式网络计算环境构建GNSS数据并行处理软件平台，为规模不断增长的GNSS数据的高效处理提供更加有效的实现途径，将成为下一步的研究方向。
| [1] | CAI Hua. Application Research of Method of Large GNSS Network Realtime Data Rapid Solution[D]. Wuhan University, 2010. (蔡华. GNSS大网实时数据快速解算方法应用研究[D]. 武汉: 武汉大学, 2010.) |
| [2] | GE M, GENDT G, DICK G. A New Data Processing Strategy for Huge GNSS Global Networks[J]. Journal of Geodesy, 2006, 82:199-203. |
| [3] | BLEWITT G. Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing: Ambizap[J]. Journal of Geophysical Research, 2008, 113(B12): 410-416. |
| [4] | CHEN Xiandong. Application of Ambizap Algorithm in Large GPS Network and Its Test Results[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 10-13. (陈宪冬. Ambiazp方法在大规模GPS网处理中的应用及结果分析[J]. 武汉大学学报:信息科学版, 2011, 36(1):10-13.) |
| [5] | SONG Lijie, OUYANG Guichong. A Fast Method of Solving Partitioned Adjustment for Super Large-scale Geodetic Network[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 204-207. (宋力杰,欧阳桂崇. 超大规模大地网分区平差快速解算方法[J]. 测绘学报, 2003, 32(3): 204-207.) |
| [6] | BOOMKAMP H. Global GPS Reference Frame Solutions of Unlimited Size[J]. Advances in Space Research, 2010, 46: 136-143. |
| [7] | DACH R, HUGENTOBLER U, FRIDEZ P, et al. User Manual of the Bernese GPS Software Version 5.0[M]. Bern: Stampfli Publications AG Press, 2008: 1-5. |
| [8] | CAO Zhebo, LI Qing. Research and Design of Parallel Programming Model on Multi-core[J]. Computer Engineering and Design, 2010, 31(13): 2999-3002. (曹折波, 李青. 多核处理器并行编程模型的研究与设计[J]. 计算机工程与设计, 2010, 31(13): 2999-3002.) |
| [9] | ZOU Xiancai, LI Jiancheng, WANG Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641. (邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641.) |
| [10] | ZHOU Weiming. Multi-core Computing and Programming[M]. Wuhan: Huazhong University of Science and Technology Press, 2008: 5-7. (周伟明. 多核计算与程序设计[M].武汉:华中科技大学出版社, 2008: 5-7.) |
| [11] | BABOULIN M, GIRAUD L, GRATTON S, et al. Parallel Tools for Solving Incremental Dense Least Squares Problems: Application to Space Geodesy[J]. Journal of Algorithms & Computational Technology, 2009, 3(1): 117-133. |
| [12] | WILKNSON B, ALLEN M. Parallel Program Design[M]. LU Xinda trans. Beijing: China Machine Industry Press, 2002: 41-50. (WILKNSON B, ALLEN M. 并行程序设计[M]. 陆鑫达,译. 北京: 机械工业出版社, 2002:41-50.) |
| [13] | CHEN Guoliang, AN Hong, CHEN Ling, et al. Practice of Parallel Programming[M]. Beijing: Higher Education Press, 2004:480-486.(陈国良, 安虹, 陈崚, 等. 并行算法实践[M]. 北京: 高等教育出版社, 2004: 480-486.) |
| [14] | CHENG Yingyan, CHENG Pengfei, GU Dansheng, et al. Data Processing Method for Combined Adjustment of National Astro-geodetic Network and GPS2000 Network[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2): 148-151. (成英燕, 程鹏飞, 顾旦生, 等. 天文大地网与GPS2000网联合平差数据处理方法[J]. 武汉大学学报: 信息科学版, 2007, 32(2): 148-151.) |
| [15] | CUI Xizhang, YU Zhongchou, TAO Benzao, et al. Adjustment in Surveying[M]. Beijing: Publishing House of Surveying and Mapping, 1982. (崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 北京: 测绘出版社, 1982.) |
| [16] | XU G C. GPS Theory, Algorithms and Applications[M]. 2nd ed. Berlin: Springer, 2007. |
| [17] | WANG Gangqiang, ZHONG Cheng, KE Qi. Fast Fourier Transform Parallel Algorithm on Multi-core Computer[J]. Computer Engineering, 2011, 37(16): 57-59. (王刚强, 钟诚, 柯琦.多核计算机上的快速傅里叶变换并行算法[J]. 计算机工程, 2011, 37(16): 57-59.) |
| [18] | YU Lei, LIU Zhiyong, SONG Fenglong, et al. Study on Instruction Scheduling of LU Decomposition on Many-core Architecture Simulator[J]. Journal of System Simulation, 2011, 23(12): 2603-2610. (余磊, 刘志勇, 宋风龙, 等. LU分解在众核结构仿真器上的指令级调度研究[J]. 系统仿真学报, 2011, 23(12): 2603-2610.) |
| [19] | LI Changgui, LU Zhiping, WANG Peng, et al. Fast Resolution of Multi-session GPS Carrier Phase Measurement Based on Grid[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 133-141. (李昌贵, 吕志平, 王鹏, 等. 基于网格的多时段GPS载波相位测量快速解算[J].大地测量与地球动力学, 2010, 30(4): 133-141.) |
| [20] | HILLAR G C. Professional Parallel Programming with C#: Master Parallel Extensions with .NET4[M]. ZHEN Siyao, FANG Peici, trans. Beijing: TSinghua University Press, 2012. (HILLAR G C. C#并行编程高级教程: 精通.NET4 Parallel Extensions[M]. 郑思遥, 房佩慈, 译. 北京: 清华大学出版社, 2012.) |
| [21] | SONG Lijie. Survey Adjustment Program Design[M]. Beijing: National Defense Industry Press. 2009. (宋力杰. 测量平差程序设计[M]. 北京:国防工业出版社, 2009.) |