线目标间存在多种空间拓扑关系约束条件,是数据组织、更新与一致性检查的基础[1, 2]。例如在空间数据增量更新中,河流往往相对稳定,道路为基础设施,发展迅速。新修道路后,一般通过外业测量新增道路的空间位置,再通过与已有地图数据进行叠加,通过拓扑关系计算、语义规则等方法来处理一致性冲突、构建变化后的河流等。如新修道路与已有河流间如存在“交叉”关系则被认为是存在冲突,需要插入桥梁或隧道等符号;而存在“相接”关系在某些比例尺中则是合理的。道路和较小河流在中小比例尺中常用线目标来表达,如在图 1中(见文末),亮红色线表示更新后的道路,绿色线表示已有地图中的河流。图 1(a)、图 1(c)表示的是“交叉”关系,表示道路跨越了河流,需要插入桥梁或隧道符号。图 1(b)表示的是“相接”关系,可能是合理关系,或道路与河流平行,由于表达的尺度和精度等原因导致道路与河流重叠。因此线目标间的相接、交叉关系的区分在空间更新与质量控制处理中有着重要作用。
图 1中的道路跨越河流的拓扑关系在目前通用的4I、9I模型中都表达为“内部/内部”有交,但“内部/内部”有交又包括多种细分情况,如交点的“相接”、“交叉”,交线的“相接”、“交叉”等,而4I、9I模型不能区分上述细分情况。
近年来,随着拓扑关系研究与应用的深入发展,国内外多位学者在线/线拓扑关系的分类与细化计算方面开展了大量的研究工作,取得了可喜的研究成果。文献[3]对线/线交进行了相接、交叉类型的细化分类,但未给出具体计算算法。文献[4]提出了线线空间关系描述的拓扑链模型与线目标间拓扑关系的细化计算方法,其中涉及线/线交的相接、交叉的计算算法,但该方法仅适用于交点的相接、交叉关系的判断,不能计算交线的相接、交叉类型。文献[5]提出的线目标间拓扑关系细化计算的分解一组合方法,将线分解,计算局部拓扑关系,再将局部拓扑关系按照一定顺序组成拓扑链来表达线线之间的拓扑关系,此方法不能判断相接交线与交叉交线。文献[6]提出的GIS线目标间空间关系的集成表达方法,建立一个综合描述线目标拓扑、方向、距离关系的方法,此模型中涉及多种空间关系的度量,描述复杂,不易于交流。而在Oracle空间数据库中应用广泛的空间线线拓扑关系也只给出了11种基本空间拓扑关系查询的操作算子,文献[7]提出的基于Oracle Spatial的空间线线拓扑关系判断的实现,描述了33种线线空间关系,但并不包括相接、交叉分类[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]。
总之,目前尽管在线/线拓扑关系的描述、区分与细化计算方面取得了可喜的研究成果,但仍缺少线/线“相接”“交叉”细化类型的判断算法,不能满足数据更新、数据质量检查等对拓扑关系细化计算的应用需求。因此本文提出一种基于局部平面分割的线/线交点和交线的相接、交叉类型的判断算法。该算法采用局部平面分割的基本思想,在线/线交的邻域内,一条线将邻域平面分割成两个平面区域,通过判断另一条线中与交相连的两线段是否处于同一个平面区域,确定该交的相接、交叉类型。
2 基于局部平面分割的线/线相接、交叉类型的判断原理文献[3]将线/线交的相接、交叉类型定义为:两线lA、lB相交,如图 2所示(粗直线表示lA,细虚线表示lB),构建交的邻域,在交的邻域内,将与交点(线)相连的线段按顺时针排序,得出线段序列T(k)=(a1,a2,a3,a4)。如果同一线目标中的两线段在该序列中不相邻,称为交叉交类型,如图 2(a)、(b)所示,a1、a3属于线lA,a2、a4属于线lB;如果同一线目标中的两线段在该序列中相邻,称为相接交类型,如图 2(c)、(d)所示,即a1、a2属于线lA,a3、a4属于线lB[2]。
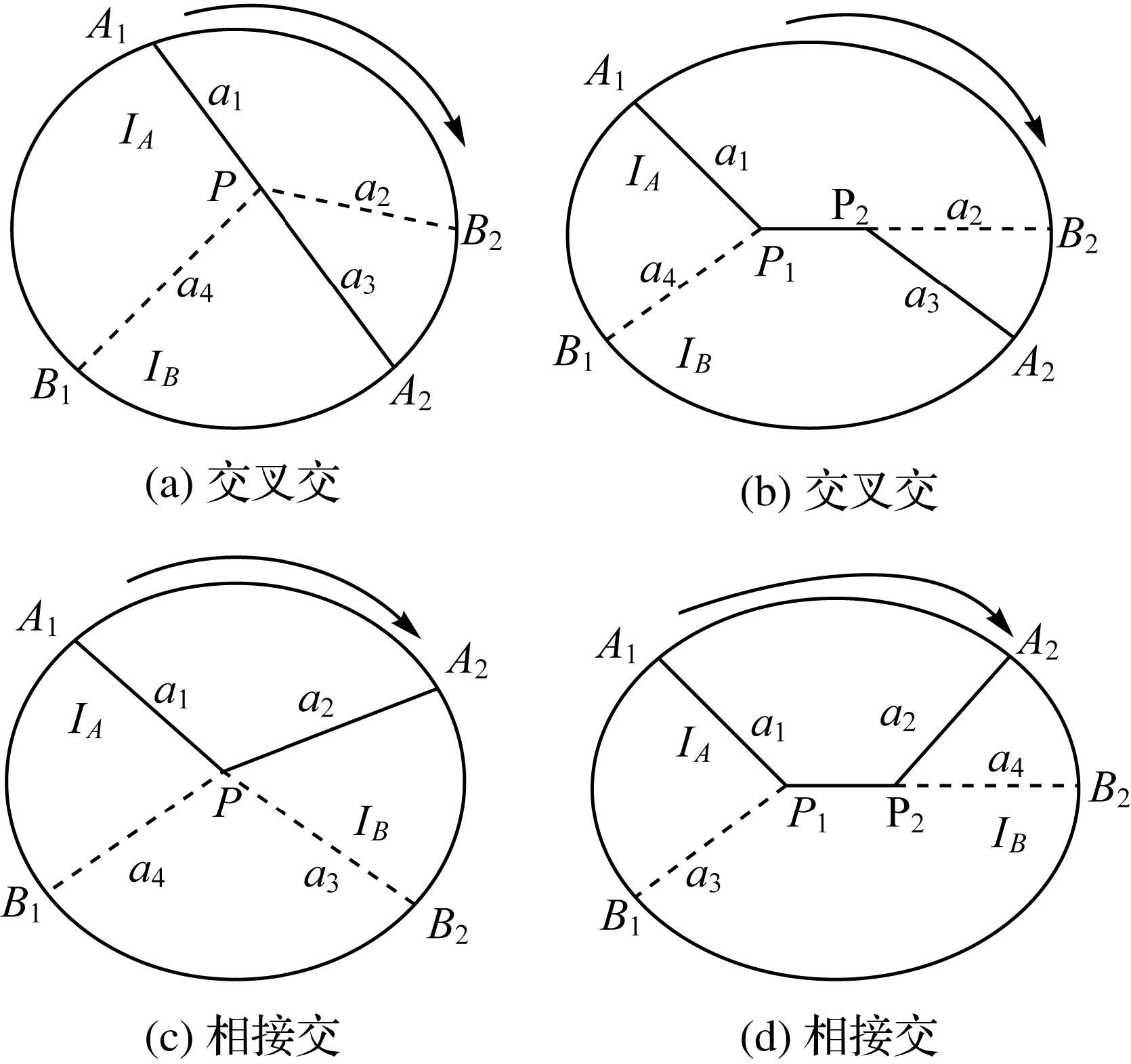
|
| 图 2 线/线交的相接、交叉定义示意图 Fig. 2 Examples of the crossing and touching intersection types |
通过分析图 2,发现交的邻域总会被线目标分割。如图 2中lA总是把邻域分成两个平面区域,lB中与交相连的两线段总会落在这两个平面区域内。而且在交叉交的邻域内,T(k)中lA、lB与交相连的线段序列相互交叉,lB中的两线段处于两个不同的平面区域。在相接交的邻域内,lB中的两线段落在同一平面区域。因此,如果可以判断lB中与交相连的两线段是否被lA分割到同一平面区域,就可以判断交的相接、交叉类型,这就是局部平面分割的思想。
应用于局部平面分割的计算几何原理是由矢量叉积的性质推出的。性质描述为:设向量M、Q,若M×Q>0,则M在Q的顺时针方向。若M×Q<0,则M在Q的逆时针方向。若M×Q=0,则M与Q共线,但可能同向也可能反向。
根据上述定理求已知坐标的两点B1、B2是否被已知线段lA1A2分割到同一平面区域,可以判断矢量叉积 与
与 的符号是否相同,总结为式(1)
的符号是否相同,总结为式(1)
此时,如果Side(lA1A2,B1,B2)值为true,那么B1、B2在线段lA1A2的同一侧,即分割到同一平面区域。这一方程可以直接应用到最简单的平面分割情况——点A1、A2与交点P在一直线上时(如图 2(a)所示),直接判断矢量 、
、 、
、 之间的关系。
之间的关系。
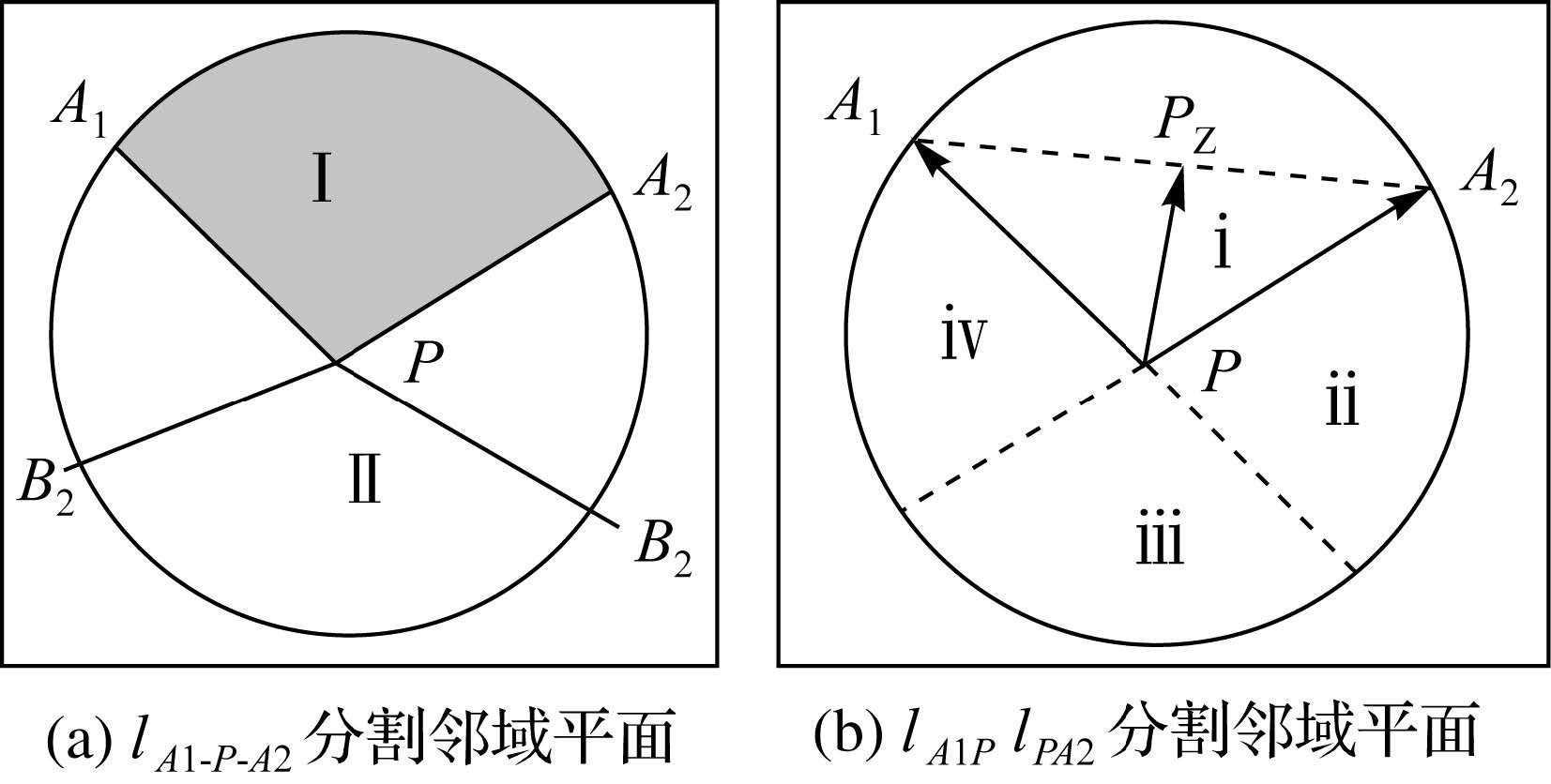
如果点A1、A2与交点P不在一直线上时,即折线段lA1PA2将邻域分割成两个平面区域Ⅰ、Ⅱ,如图 3(a)。向量 与
与 及其延长线将邻域分割成ⅰ、ⅱ、ⅲ、ⅳ4个辅助性区域,如图 3(b),此时区域Ⅰ与辅助性的区域ⅰ完全相等,选取将这一独立的辅助性区域(ⅰ区或Ⅰ区)内的一点——例如A1、A2的中点PZ,作为参考点,向量叉积
及其延长线将邻域分割成ⅰ、ⅱ、ⅲ、ⅳ4个辅助性区域,如图 3(b),此时区域Ⅰ与辅助性的区域ⅰ完全相等,选取将这一独立的辅助性区域(ⅰ区或Ⅰ区)内的一点——例如A1、A2的中点PZ,作为参考点,向量叉积 ×
× 与
与 ×
× 的正负符号就代表了Ⅰ区内任一以点P为起点的向量与
的正负符号就代表了Ⅰ区内任一以点P为起点的向量与 与
与 叉积的结果。如果判断
叉积的结果。如果判断 、
、 是否在同一平面区域,只需要将(
是否在同一平面区域,只需要将( ×
× ,
, ×
× )、(
)、( ×
× ,
, ×
× )与(
)与( ×
× 、
、 ×
× )作比较,分别判断
)作比较,分别判断 、
、 与
与 是否在同一区域,当
是否在同一区域,当 、
、 与
与 都在同一区域或都不在同一区域时,交点是相接交,否则是交叉交。以判断
都在同一区域或都不在同一区域时,交点是相接交,否则是交叉交。以判断 与
与 是否在同一区域为例,总结为式(2)
是否在同一区域为例,总结为式(2)
如果Side(lA1PA2,B1,PZ)的值是true,那么 与
与 在同一区域。同理可以判断
在同一区域。同理可以判断 。
。
|
| 图 3 折线段分割局部平面的计算原理 Fig. 3 The calculation principle of segment splitting the disc |
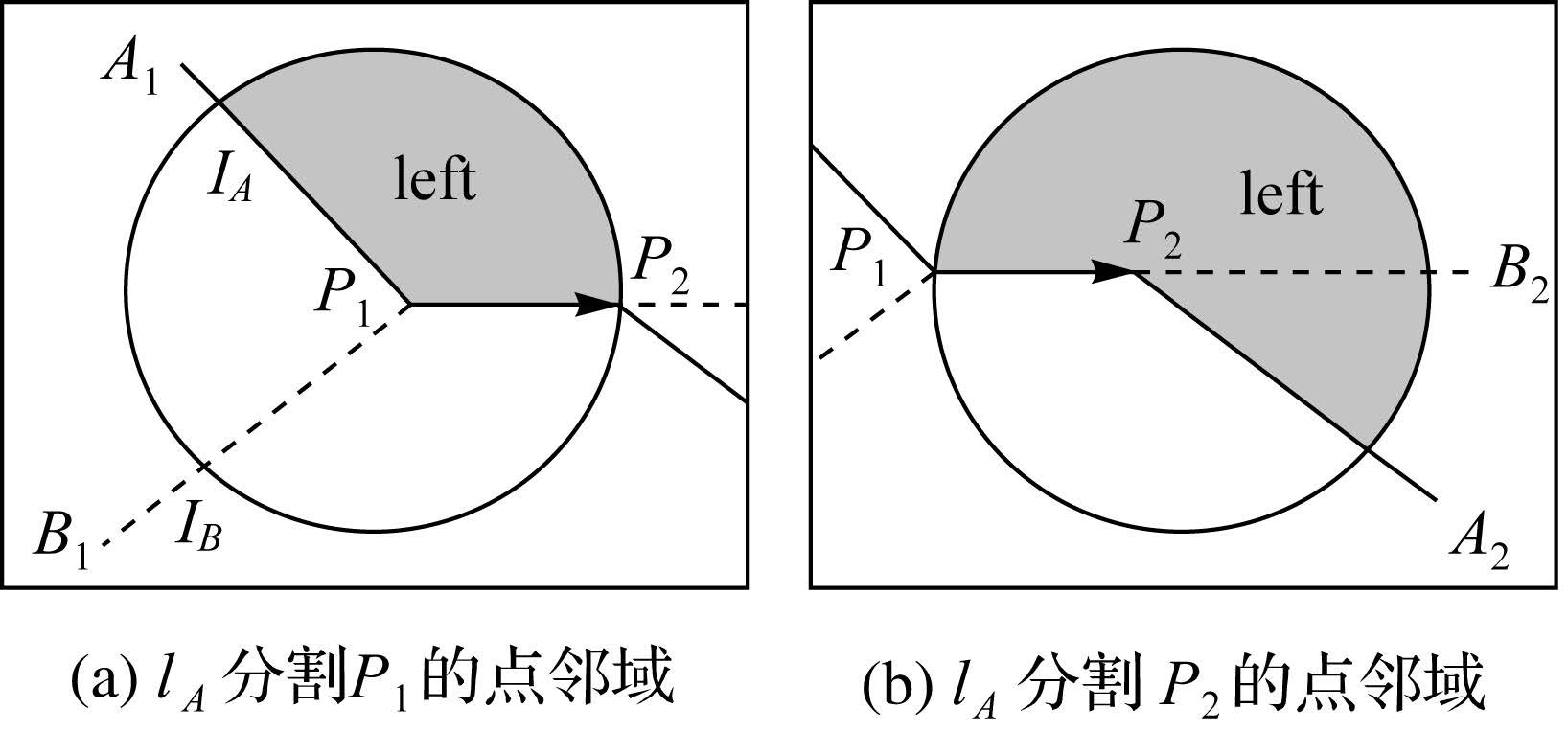
利用式(1)和式(2)可以计算所有相接/交叉的交点类型。而交线的邻域中存在更复杂的平面分割,如图 2(b)、(d)。此时需要进行简化。如果分别以交线的首尾节点P1、P2为圆心做辅助性的节点圆形邻域,如图 4(a)、(b),那么在每一个节点圆形邻域内,线lA都将邻域圆分割为两个不同的区域。引入交线的方向P1→P2,被分割的平面区域统一就归纳为lP1→P2的左侧区域与lP1→P2的右侧区域。此时,利用上述分割定理分别确定PB2、PB1处于节点圆邻域中的左侧区域还是右侧区域,就可以判断B1、B2是否处于lP1→P2的同一侧。
|
| 图 4 交线相接/交叉类型的计算方法 Fig. 4 The method of dividing line intersections into touching and crossing |
假设:线lA、lB相交于点P,lA中与点P相连的形状点为A1、A2,lB中与点P相连的形状点为B1、B2。
此时,基于上述理论,在线/线交点的邻域中,选取lA将邻域分割为两个平面区域。由于分割线的类型不同,使用的原理也不同。所以,先判断lA在邻域内的部分是否是直线段。判断方法:交点P是否是lA的形状点。
如果P不是lA的形状点,那么lA在邻域内的部分是直线段。将矢量 代入式(1),判断
代入式(1),判断 的值,如果Side(lPA2,B1,B2)=true,那么B1、B2在被分割到同一平面区域,交点P是相接;如果Side(lPA2,B1,B2)=False,那么B1、B2被分割到不同平面区域,交点P是交叉。总结为规则一。
的值,如果Side(lPA2,B1,B2)=true,那么B1、B2在被分割到同一平面区域,交点P是相接;如果Side(lPA2,B1,B2)=False,那么B1、B2被分割到不同平面区域,交点P是交叉。总结为规则一。
规则1:P不是形状点
如果Side(lPA2,B1,B2)值为真,那么交点P是相接交,否则交点P是交叉交。
如果P是lA的形状点,计算lA1A2的中点PZ,分别将 代入式(2),如果Side(lA1PA2,B1,PZ)=true,那么B1与点PZ被分割到同一平面区域。同理,如果Side(lA1PA2,B2,PZ)=true,那么B2与点PZ被分割到同一平面区域。如果B1、B2被分割到同一平面区域,那么交点P是相接。如果B1、B2被分割到不同平面区域,那么交点P是交叉。总结为规则2。
代入式(2),如果Side(lA1PA2,B1,PZ)=true,那么B1与点PZ被分割到同一平面区域。同理,如果Side(lA1PA2,B2,PZ)=true,那么B2与点PZ被分割到同一平面区域。如果B1、B2被分割到同一平面区域,那么交点P是相接。如果B1、B2被分割到不同平面区域,那么交点P是交叉。总结为规则2。
规则2:P是形状点
如果Side(lA1PA2,B1,PZ)∧Side(lA1PA2,B2,PZ)值为真,那么交点P是交叉交,否则交点P是相接交。
3.2 交线相接\交叉类型计算规则
假设:线lA、lB相交于线lP1P2,交线lP1P2的端点是P1、P2,lA中分别与点P1、P2相连的形状点为A1、A2,lB中分别与点P1、P2相连的形状点为B1、B2。
此时,可以利用直线分割平面原理进行计算。引入lA的方向,交线的方向P1→P2,这两个方向必须完全一致。此时,在P1的节点圆形邻域中确认B1的左右位置,在P2的节点圆形邻域中确认B2的左右位置,就可以求出B1相对lA的左右位置的值,用Right(lA,B1)表示,值为布尔型,B1在lA的右侧时值为真,B2相对lA的左右位置Right(lA,B2),就可以总结出交线lP1P2的类型。
以求点B1的位置为例,查找交线中与P1相连的节点Pf,第一步同样是判断A1→P1→Pf是否是一直线段。判断方法可以采用:判断交线节点P1是否是lA的形状点。
如果P1不是lA的形状点,那么lA在节点邻域邻域内的部分是直线段,根据 ×
× 的叉积结果判断
的叉积结果判断 与向量
与向量 (与P1→P2的方向一致)的左右关系,如果
(与P1→P2的方向一致)的左右关系,如果 ×
× <0,那么Right(lA,B1)=True,
<0,那么Right(lA,B1)=True, 在lA的右侧。
在lA的右侧。
规则3:P不是形状点
Right(lA,B1)= ×
× <0 ?true:false
<0 ?true:false
如果P1是lA的形状点,此时求B1与lA1P1Pf的左右关系。求出A1、Pf的中点PZ1,将向量代入式(2),求出( ×
× )·(
)·( ×
× )>0&(
)>0&( ×
× )·(
)·( ×
× )>0的值,确认B1与PZ1是否分布在同一区域。根据规则3计算PZ1与有向线lA的左右位置关系Right(lA,PZ1)=
)>0的值,确认B1与PZ1是否分布在同一区域。根据规则3计算PZ1与有向线lA的左右位置关系Right(lA,PZ1)= ×
× <0 ?true:false。如果B1与点PZ1被分割到同一平面区域,B1与点PZ1所处的左右位置关系相同;如果B1与点PZ1被分割到不同的平面区域,B1与点PZ1所处的左右位置关系相反。总结为规则4。
<0 ?true:false。如果B1与点PZ1被分割到同一平面区域,B1与点PZ1所处的左右位置关系相同;如果B1与点PZ1被分割到不同的平面区域,B1与点PZ1所处的左右位置关系相反。总结为规则4。
规则4:P是形状点
如果Side(lA1P1Pf,B1,PZ1)值为真,那么Right(lA,B1)=Right(lA,PZ1),否则Right(lA,B1)=﹁ Right(lA,PZ1);
同理可以判断B2,查找交线中与P2相连的节点Pl,计算的关键在于统一交线的方向,即确定Pl→P2→A2的方向与P1→P2的方向一致。这样才能确保求得的B1、B2的左右位置是绝对的。最后,总结B1、B2的左右位置得出交线的类型,总结为规则5。
规则5:如果Right(lA,B1)∧Right(lA,B2)值为真,那么交线lP1P2是交叉交,否则交线lP1P2是相接交。
4 试验实现总结3.1与2.2,可以将线线交的相接\交叉类型计算归纳如下。
假设:线lA与线lB,求出两线的交类型。函数Inter(lA,lB)为求线lA与线lB的交。定义PZ为变量点对(q1,q2)的中点;定义lA的节点与形状点为点集shapept。Right(lA,B1)是求点B1与有向线lA的左右方向的函数,值为布尔型,B1在lA的右侧时值为真。
(1)Inter(lA,lB)得出交集,其中交点集为Pt,交线集为Line。
(2)求交点集Pt中的每一个元素Pt[i]的相接\交叉类型。查找lA中与Pt[i]相连的节点A1、A2,lB中与Pt[i]相连的节点B1、B2。如果Pt[i]与shapept中的元素相等,令PZ为(A1,A2)的中点,进行Side(lA1PA2,B1,PZ)∧Side(lA1PA2,B2,PZ)运算,值为真时点Pt[i]是交叉,值为假时点Pt[i]是相接,利用规则一求出Pt[i]的类型;如果Pt[i]与shapept中的元素全不相等,进行Side(lPA2,B1,B2)运算,值为真时点Pt[i]是相接,值为假时点Pt[i]是交叉。
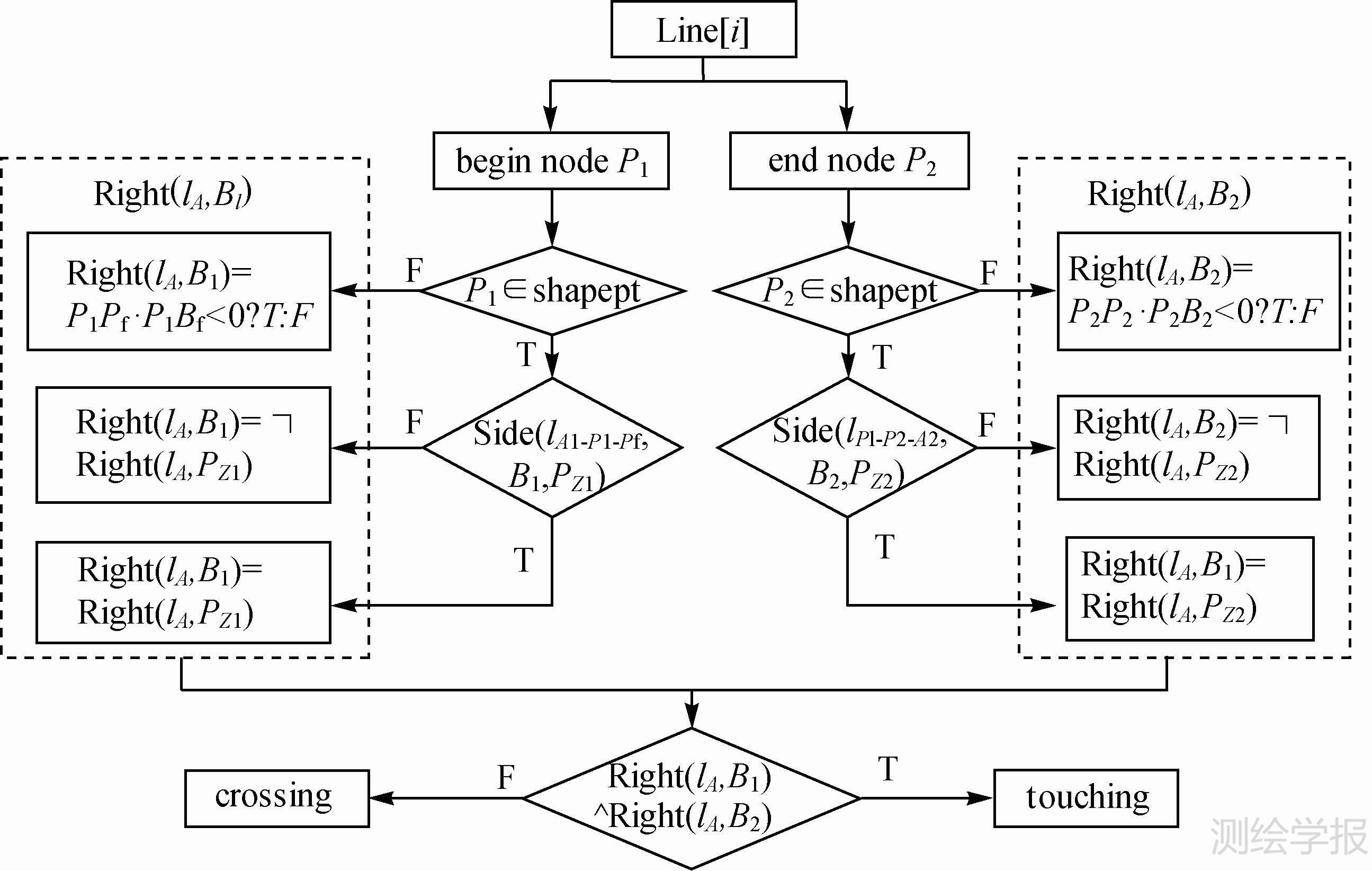
(3)求交线集Line中的每一个元素的类型。计算的流程总结如图 5所示。其中,Line[i]表示交线集Line中元素,头结点为P1,尾节点为P2。A1是lA中与P1相连的节点,Pf是Line[i]中与P1相连的节点,B1是lB中与P1相连的节点。如果P1→A1→Pf在一条直线上,即P1是形状点shapept,利用规则3求出B1的左右位置,其中lA1Pf表示由点A1→Pf的有向线段。否则,令PZ为(P1,Pf)的中点,利用规则4求出B1的左右位置,其中lA1P1,lP1Pf表示由点P1、A1与P1、Pf构成的两条直线段。lA中与P2相连的节点是A2,Line[i]中与P2相连的节点是Pl,lB中与P2相连的节点是B2。如果Pl→P2→A2在一条直线上,利用规则3求出B2的左右位置;否则,令PZ为(P2,Pl)的中点,利用规则4求出B2的左右位置。最后规则5求出Line[i]的类型。

|
| 图 1 道路线与河流线相交的3种细分类型 Fig. 1 Three intersection types including between rivers and roads |
|
| 图 5 交线相接\交叉计算流程 Fig. 5 Calculation flow chart of dividing intersections into touching and crossing |
为了验证本文的方法与模型,在增量采编原型系统上,用Visual Studio 2008的C#编程实现了基于局部平面分割的线/线交相接、交叉类型计算方法。
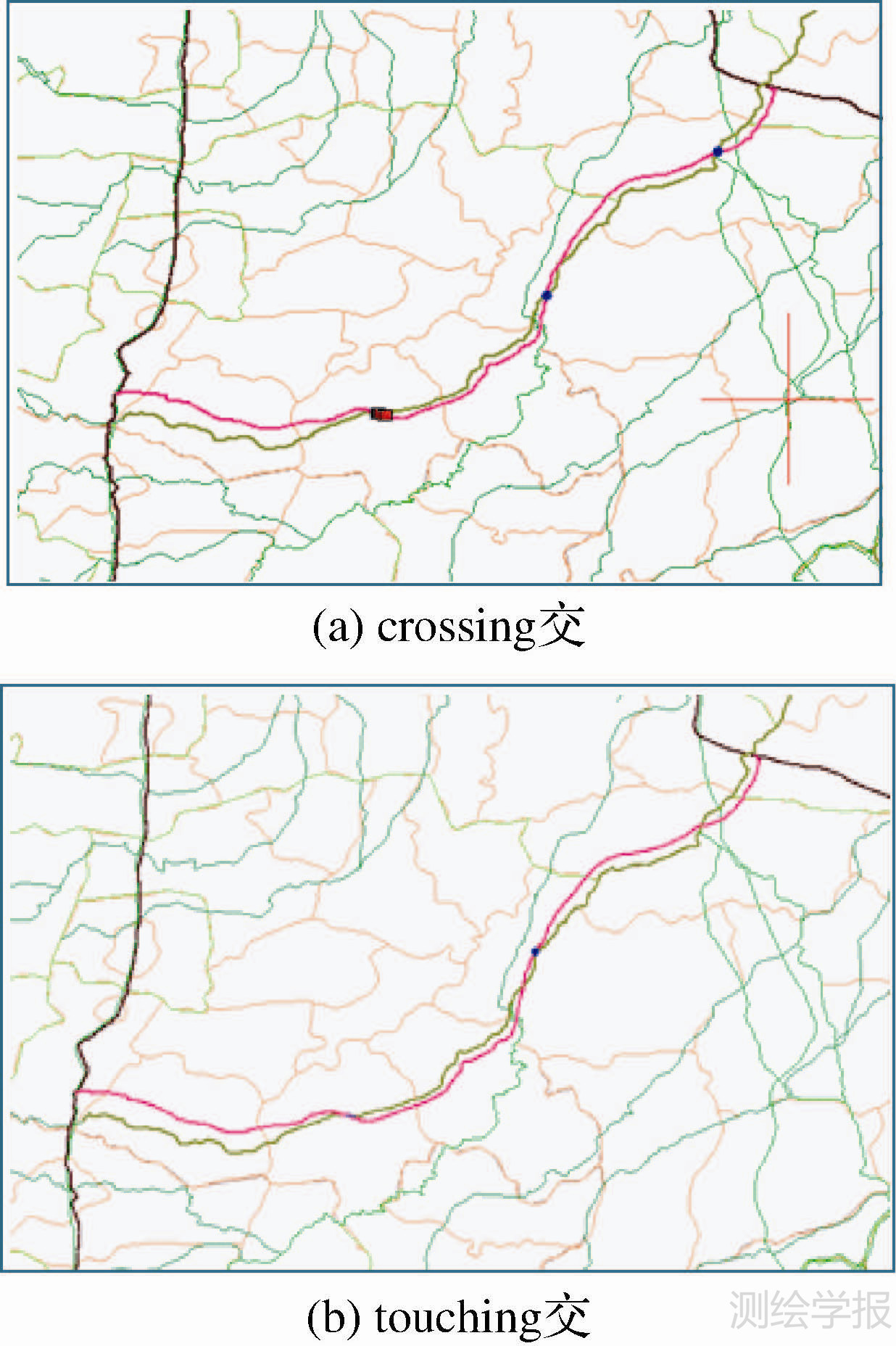
图 6是一幅1∶25万中国行政区道路与河流网地形图的局部,其中,道路经过更新,图中红色的线表示更新后的道路,绿色线表示河流。选取这一条更新后的道路线(红色粗实线),与一条相交的河流线(深绿色粗实线),用本文提出的方法计算了该道路线与该河流线之间相接、交叉交的类型,并且分别用蓝色高亮显示相接交与交叉交。计算结果如图 6所示,(a)图中高亮显示了两条线的交叉交,包括一条交线与两个交点,(b)图中高亮显示了两条线的相接交,只有一个交点。试验验证了本文计算方法的正确性。可以在判断相接、交叉类型的基础上进行下一步处理,在交叉交的位置按照实际情况插入跨河的桥梁或隧道。
|
| 图 6 试验实例图 Fig. 6 Data of test |
论文阐述了直线分割平面的计算原理,根据几何代数中直线分割平面定理,按照一条直线分割平面、两条相交直线分割平面和有向直线段分割平面3种情况推导出3个原理方程;提出了计算交相接/交叉类型时的5条规则,分别适用于交点邻域中的两种不同的分割情况和交线头尾节点邻域中的两种不同的分割情况;给出了线线交叉、相接交分类计算的算法流程。最后,在数据更新系统平台中用Visual Studio 2008的C#编程实现了该方法,并以中国道路与河流网为实验数据进行了试验,验证了算法的正确性。
目前在拓扑关系描述区分方面的模型较多,但在拓扑关系细化计算方面的成果仍不能满足应用需求。因此本文的后续研究工作包括:① 将继续研究线线拓扑关系的其他细化算法,并考虑将线线交叉、相接细分类型判断算法应用到线面拓扑关系的细化计算中;② 探索线线交叉、相接细分类型的实际应用,如,GIS不同类型线要素间具有交叉、相接关系类型在数据库更新中所对应的目标重构与更新处理方法,在数据质量控制中对应的冲突类型与处理算法等。
| [1] | ZHOU Xiaoguang. Incrmental Updating of Cadastral Database[M].Beijing: Surveying and Mapping Press,2007.(周晓光. 地籍数据库增量更新[M]. 北京:测绘出版社,2007.) |
| [2] | XING Hanfa, ZHOU Xiaoguang. Local Contour Line Fusion Based on Line /Line Topological Relations[J]. Geomatics and Information Science of Wuhan University,2010,35(11): 1322-1326. (邢汉发,周晓光. 基于线/线拓扑关系的局部变化等高线融合[J]. 武汉大学学报:信息科学版,2010,35(11):1322-1326.) |
| [3] | CLEMENTINI E, DIFELICE P. Topological Invariants for Lines[J].IEEE Transactions on Knowledge and Data Engineering, 1998,10:38-54. |
| [4] | ZHOU Xiaoguang, CHEN Jun. Computation of Topological Relations between Cadastral Objects Based on Euler-number[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(3):291-298.(周晓光,陈军. 基于欧拉数的地籍拓扑关系计算[J]. 测绘学报,2006,35(3):291-298.) |
| [5] | CHEN Jun , LIU Wanzeng, LI Zhilin. The Refined Calculation Method of Topological Relationships between Line Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(3):255-260. (陈军,刘万增. 线目标间拓扑关系的细化计算方法[J]. 测绘学报,2006,35(3):255-260) |
| [6] | DENG Min, LI Zhilin. An Integrated Approach to Representing Line-line Spatial Relations in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(4):421-427.(邓敏,李志强. GIS线目标间空间关系的集成表达方法[J]. 测绘学报,2007,36(4):421-427.) |
| [7] | WANG Lijiang, YUE Guoshen. The Realization of Differentiating Spatial Topological Relations between Lines Based on Oracle Spatial[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(1):78-82.(王礼江,岳国森. 基于Oracle Spatial的空间线线拓扑关系判断的实现[J]. 测绘学报,2006,35(1):78-82.) |
| [8] | LIU Wanzeng,CHEN Jun. A Topology Chain Model for Describing Line-line Spatial Relations[J]. Journal of China University of Mining & Technology, 2010,39(1):75-79. (刘万增,陈军. 线线空间关系描述的拓扑链模型[J]. 中国矿业大学学报,2010 ,39(1):75-79.) |
| [9] | NI Jianhua, ZHOU Xiaoguang. The Computation of Basic Line/Line Topological Relations Based on Line Segment[J]. Geomatics World, 2009,10(5):39-43. (倪建华,周晓光. 基于线段的基本线/ 线拓扑关系计算[J]. 地理信息世界,2009,10(5):39-43.) |
| [10] | LIU Wanzeng, CHEN Jun. Automatic Detection of Spatial Conflicts between Line Objects[J]. Journal of China University of Mining & Technology,2006,35(6): 767-771.(刘万增,陈军. 线目标空间冲突自动检测方法研究[J].中国矿业大学学报,2006,35(6):767-771. |
| [11] | EGENHOFER M,FRANZOSA R. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems,1991,5(2): 161-174. |
| [12] | EGENHOFER M. A Model for Detailed Binary Topological Relations[J]. Geomatica,1993,47 : 261-273. |
| [13] | MAX J. Modeling Conceptual Neighborhoods of Topological Line-Region Relations[J]. International Journal of Geographical Information Science,1995,9(5):555-565. |
| [14] | NEDAS K A, EGNHOFER M J. Metric Details of Topological Line-line Relations[J]. International Journal of Geographical Information Science,2007,1(21):21-48. |
| [15] | DENG M, CHENG T, CHEN X, et al. Multi-level Topological Relations between Spatial Regions Based upon Topological Invariants[J], Geoinformatica, 2007, 11: 239-267. |
| [16] | LI S. A Complete Classification of Topological Relations Using the 9-intersection Method[J], International Journal of Geographical Information Science, 2006,20:589-610. |
| [17] | LI S, LIU W. Topological Relations between Convex Regions[J].Proceedings of the Twenty-fourth AAAI Conference on Artificial Intelligence, 2010,AAAI-10: 321-326. |
| [18] | CHEN J, LIU W. Detection of Spatial Conflicts between Rivers and Contours in Digital Map[J]. International Journal of Geographical Information Science,2007,21(10):1093-1114. |
| [19] | CHEN Jun, ZHAO Renliang. Spatial Relations in GIS: A Survey on Its Key Issues and Research Progress[J]. Acta Geodaetica et Cartographica Sinica, 1999,28(2):95-102. (陈军,赵仁亮. GIS 空间关系的基本问题与研究进展[J]. 测绘学报,1999,28(2):95-102.) |
| [20] | DENG Min, ZHAO Binbin, XU Zhen.Representation Methods of Distance between Spatial Objects in GIS and Their Analysis[J].Computer Engineering and Applications,2011,47(1):35-39.(邓敏,赵彬彬,徐震. GIS空间目标间距离表达方法及分析[J]. 计算机工程与应用,2011,47(1):35-39.) |
| [21] | LIU Wanzeng, CHEN Jun. Detecting the Spatial Inconsistency between the Updated Rivers and Valleys[J]. Journal of Image and Graphics,2008,13(5): 1003-1008.(刘万增,陈军.数据库更新中河流与山谷线一致性检测[J].中国图象图形学报,2008,13(5):1003-1008.) |
| [22] | ZHOU P. Calculating Geometry: Design and Analysis of Arithmetic [M]. Beijing:Tsinghua University Press,2011.(周培德. 计算几何--算法设计与分析[M].北京:清华大学出版社,2011.) |





