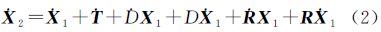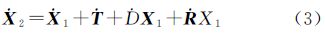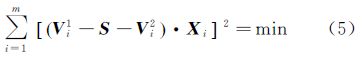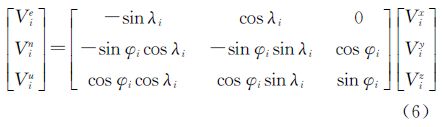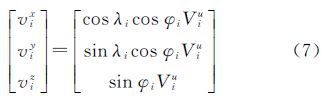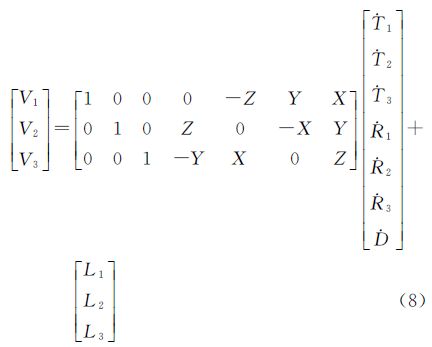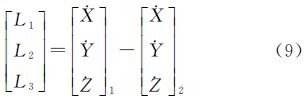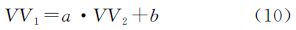2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geoinformation Engineering,Xian 710054,China
1 引 言
研究地壳的垂直运动对于建立更合理、更高精度的全球坐标框架有重大意义[1],而研究和确定全球的垂直基准,则有着重要的作用和意义。关于全球垂直地壳运动的参考基准,目前国际上还没有统一的基准,也没有统一的实现方法。对于同一个台站的垂向分量,全球各空间大地测量数据分析中心公布的数据也是形式各异;由于全球垂直地壳运动参考基准的不统一,世界各个国家和地区已有的垂直运动数据难以统一使用。这种状况不仅会造成在大地测量学领域理解和应用上的混乱,而且还会制约观测结果在地震、地质和地球物理等各领域的应用,甚至会产生误导。
国内外一些学者和数据分析中心曾作了一些探讨性和验证性的研究。文献[2]利用冰期后地壳回弹模型初步研究了垂直地壳运动的参考基准。文献[3]指出均衡基准在研究我国大陆现今垂直地壳运动有其不适用性,因而提出了单点动态垂直基准,该基准与基本验潮站相联系,速率结果具有绝对性质,是适用于水准测量的垂直基准。文献[4, 5, 6]研究了区域垂直地壳运动的参考基准,该基准基于地壳均衡假说,并对垂直地壳运动的形变场进行了拟合分析。文献[7, 8, 9]提出的方案没有采用全球的数据,所以建立的仍然是区域基准,况且地壳均衡基准假说已被基于空间技术的全球构造变化研究结果证明不太准确。文献[10, 11, 12, 13]对地壳的水平运动及其速度场进行了研究,但对全球性的垂直运动及其基准鲜有提及。国际上,一些学者也作了相关的研究,比如文献[14]综合利用卫星测高和水准数据构建了区域的垂直基准IGLD85,而在文献[15]中,仅新西兰就有13个独立的区域垂直基准,该状况极不利于地壳运动观测数据的享用及其在各个领域的应用。国际上各空间观测数据分析中心给出的全球台站的地壳运动速度场,均是以NNR-NUVEL1A 绝对板块运动模型得到的速度矢量作为约束,采用一个或多个参考台站建立起来的,而NNR-NUVEL1A模型只能给出台站水平方向的运动速度[16, 17],这表明其隐含的约束条件是选用的参考台站的垂向速度有可能为零。而实际情况是:①这些参考台站在垂直方向上有不同程度的运动变化;②国际上各个空间观测数据分析和处理中心选择的参考台站不完全一样。以上原因造成了全球垂直地壳运动参考基准的不统一和不准确。
从理论上来分析,地壳的垂直运动应定义为相对于地球质心的运动,利用不同技术观测同一个测站得到的垂向速度也应该相同。但实际上,由于全球各地区的垂向运动基准不同,导致一些数据分析中心或全球各区域在数据处理时得到的结果也不同,即使同一个测站,当采用不同的观测技术时,得到的速率值也有差异,这就限制了空间观测技术在国民经济建设中的应用。因此,有必要将各数据分析中心给出的速度场进行统一,建立一个全球统一的垂直地壳运动参考基准,而对全球垂直地壳运动的参考基准问题进行深入系统的研究也是当前地球构造学科比较迫切的事情,本文基于上述研究背景,提出一种建立全球垂直地壳运动参考基准的方法,该基准具有明确的地球物理意义,而且易于实现、便于应用,适合作为全球统一的垂直地壳运动参考基准。
2 数 据本文所用数据来自国际地球参考框架(the international terrestrial reference frame,ITRF),包括ITRF2005和ITRF2008中SLR、甚长基线干涉测量技术(very long baseline interferometry,VLBI)、GPS 3种技术各自数据分析中心解算后的站坐标和速度场的数据,其观测历元分别是2000.0和2005.0,下列数据序列均可在ITRF的官方网站获取到。
SLR速度场的数据包含ITRF2008_SLR。ITRF2008_SLR是由各分析中心提交给IERS的坐标解,时间跨度为1983.0-2009.0,历时26年的观测数据,站速度的精度大部分优于3 mm/a。
VLBI速度场的数据包含ITRF2008_VLBI和ITRF2005_VLBI,ITRF2008_VLBI坐标解的时间跨度为1980.0-2009.0,共有历时29年的观测数据,参考历元为2005.0,数据为VLBI观测站的地心坐标和测站的地心坐标速度。地心坐标精度为3 mm左右,地心坐标速度的精度大部分好于3 mm/a。ITRF2005_VLBI.SCC采用了1992年9月-2005年9月跨度的时间序列数据,站速度的精度大部分好于3 mm/a。
GPS速度场的数据包括ITRF2008_GNSS和ITRF2005_GPS,ITRF2008_GNSS.SCC的时间跨度为1997.0-2009.5,历时12年半的观测数据,获得的地心坐标标称精度优于1 mm,站速度的精度在1 mm/a以内;ITRF2005_GPS.SCC包含了1996.0-2006.0年间GPS的相位观测数据,其地心坐标标称精度大都优于1 mm,水平站速度的精度大都在0.2 mm/a以内,垂向站速度的精度在1 mm/a以内。
并址站信息由国际地球自转服务(International Earth Rotation Service,IERS)提供,发布时间为2010-04-01。
在数据预处理时,主要考虑了以下几个方面:① 台站站速度每一分量的方差是否好于3 mm/a。② 台站是否位于形变板块的边界区或板块内明显的构造形变区。③ 并址站站速度的3个分量是否保持在同一方向和同一量级上。综合应用上述标准,可以初步判断所选测站和并址站的观测精度以及测站的稳定性如何。
3 方 法 3.1 可行性分析卫星激光测距SLR技术经过40多年的发展,单次测量精度已经达到亚厘米级,是目前空间大地测量中精度最高的技术之一,也是目前监测地球质心运动最精确的空间大地测量工具[18]。利用SLR技术能够直接测定地面台站相对于地球质心的坐标,因此,该技术测定的测站垂向速度也是相对于地心的运动速度。由于地心运动反映了地球内部及各圈层的复杂运动和相互作用过程,因此,相对于地心的垂向运动就可以作为地壳垂直运动的参考基准。
而将地心作为参考点的话,必然要考虑地球质心的运动变化。地球质心是指整个地球(包括海洋和大气)的质量中心,它是唯一的。地球质心的运动有两种:一种是地球质心在空间的运动,例如地球质心绕太阳的公转运动;另一种是地球质心在固体地球内部的运动,它是由地球内部质量分布变化引起的。整个地球(包括海洋和大气)是一个封闭的保守系统,由于动量守恒,理论上地球内部质量分布变化不会影响地球质心在空间的运动,而只会导致地球质心在固体地球内部的位置产生变动。目前国内外研究的热点均是指后一种地球质心运动。
地球质心运动是一个十分复杂的过程,既有短期或短周期项,也有长期或长周期项。文献[19]根据当时的观测和理论计算,表明在30 d到10 a的时间尺度上,地球质心运动的量级在1 cm之内,主周期为周年项,次周期为半年项,主要起因于大气、海洋和地表水分布的季节性变化。并根据地球质心的运动规律,在其主周期内求定一个平均地球质心位置,称为协议地球质心,瞬时地球质心相对于协议地球质心的各种短期或周期项变化,可在解算测站平坐标时直接加以改正,而长期或长周期变化则反映在测站平坐标的变化中。文献[20]利用SLR对LAGEOS 1/2卫星的距离观测,解算了1993-2006 年期间的地心运动时间序列,经分析也发现地心运动存在长期和周期性变化,而季节性变化是地心运动的主项,主要是由地球流体圈层的质量分布造成的,如海洋、大气和陆地水等。由此可见,地心运动的变化主要体现在短期或短周期项,长期或长周期项的变化不明显,而且解算时可将其反映在测站平坐标的变化中。综上所述,研究测站长期或长周期的变化,可将地心作为研究的参考点,即将SLR相对于地心的垂向运动作为地壳垂直运动的参考基准是可行的。
ITRF2008参考框架是2010年发布的,所采用的SLR技术的观测数据的跨度为1983.0-2009.0,观测历元为J2005.0,观测台站地心坐标站速度的误差大部分都在1 mm/a之内[23]。与ITRF2005一样,ITRF2008框架下的SLR技术的速度场仍是基于时间序列得到的,其观测精度和观测数量都有很大的提升。综上所述,将ITRF2008框架下SLR技术获取的垂向速度场作为全球垂直地壳运动的参考基准是可行的。下面具体讨论并建立这种全球统一的垂直运动的参考基准。
3.2 模型建立观测台站沿垂直方向的运动应定义为相对于地球质心的运动,但在实际应用中,各数据分析中心在定义其速度场的垂直运动参考架时具有一定的任意性,大都采用使一个或多个位于构造稳定区的垂直站速度约束为零的方法来定义,因此,参考架统一后的各速度场的垂直运动在概念上仍不是相对于地球质心的。而SLR 技术能够直接测定地面台站的地心坐标,在全球范围内选择观测数量较多、观测精度较高的SLR 台站,其实测垂向速度就构成了全球垂直地壳运动的参考基准。如果SLR实测垂向速度是相对于地球质心的运动,那么其他空间观测技术的速度场与SLR实测速度场之间必然会存在系统差,因此,消除各速度场与SLR实测速度场之间的系统差,可实现相对于地球质心的垂直运动参考架的统一。不同观测技术实现的参考框架之间的系统差主要体现在以下几个方面[22]:
(1) 坐标原点不一致。例如,由VLBI技术实现的参考架(VTRF)的坐标原点,则是通过给定某一VLBI和SLR的并址站的SLR地心坐标定义到地球质心,该站地心坐标的误差将导致坐标原点的偏差;另外,不同的分析中心可能采用不同台站的SLR地心坐标来定义其VTRF的坐标原点。这必将导致各VTRF之间及VTRF与其他地球参考架之间坐标原点的偏差。由SLR、LLR和GPS等空间技术实现的地球参考架虽然是由动力学技术实现的,但各种技术所采用的动力学参考系是不同的,因而所实现的地球参考架的坐标原点也不可能完全一致,况且各种动力学技术只是以一定的精度把参考架的坐标原点确定到地球质心。
(2) 尺度不完全一致。由各种空间技术实现的地球参考架的尺度是由数据处理时光速C和地球引力常数GM的采用值以及所采用的相对论改正模型共同确定的,各分析中心采用的常数和模型的不同,会导致各地球参考架尺度的不同。即使各分析中心采用完全一致的常数和模型,但因观测技术、参加平差的数据量及数据处理方法的不同,也会使尺度稍有不同。
(3) 定向的不同。采用不同历元或不同系统的地球自转参数,所定义的地球参考架的坐标轴指向是不一致的,它们之间存在着微小的旋转。例如,尽管BTS/ITRF序列采用BIH在历元1984.0的定向参数,但其他参考架却采用了各自的定义参数。
对于两个不同的参考架,要转换至同一参考架时有很多变换模型,这里采用有着广泛应用的七参数变换模型[22],即两框架之间的原点之差用3个平移参数TT1,T2,T3表示,定向之差用3个旋转参数RR1,R2,R3表示,尺度差用D表示,则两框架之间的变换关系为
式中,X1、X2两个向量分别表示两种不同观测技术实现的参考框架下并址站的站坐标。
由于板块运动、局部形变和冰期后地壳回弹等因素的影响,地球参考架中的台站坐标会随时间变化。为维持协议地球参考架的稳定,一个高精度的参考架总是对应一个时间历元和一个速度场。速度场可以由某个板块运动模型给定(如NNR-NUVEL1A[16, 17]或者APKIM05[23]),也可由观测结果导出,目前则是两者的组合。
当两个参考架的历元发生改变时,它们之间的变换参数也将发生变化。设两个参考架间变换参数的变化率为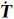 (
(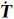 1,
1,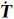 2,
2,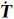 3)、
3)、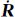 (
(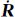 1,
1,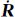 2,
2,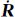 3)和,那么,将式(1)对时间t求导,则有式(2)
3)和,那么,将式(1)对时间t求导,则有式(2)
由于旋转矩阵中R(R1,R2,R3)一般小于10个毫秒,转化为弧度后为10-7~10-8量级,并且速度场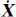 1量级为几个cm/a,所以R
1量级为几个cm/a,所以R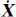 1比较小,可以略去不计;尺度参数D一般也在10-6~10-7量级,所以D
1比较小,可以略去不计;尺度参数D一般也在10-6~10-7量级,所以D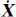 1也可略去不计,式(2)可简化为
1也可略去不计,式(2)可简化为
将式(3)展开为
式中,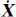 1和
1和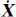 2分别对应两个不同框架下的速度场。
2分别对应两个不同框架下的速度场。
由于SLR技术获取的台站垂向运动是直接相对于地球质心的,那么其他空间观测技术的垂向运动与SLR实测的垂向运动之间必然会存在系统差,要求其系统差,必须建立两种技术的并址观测台站。而正是由于采用了不同的参考框架,使得并址站的观测数值不同。经过系统差的改正,就可以把其他技术获取的速度场统一到相对于地球质心的运动上。系统差的求解可以通过迭代的方式进行,但其前提是要利用两种不同观测技术实现的参考框架下并址站的数据进行求解,即首先将系统差作为参数在地心参考架中消除其影响,然后使各站的垂向速度与SLR相应并址站的垂向运动之差在地心方向上投影的平方和为最小来解算系统差[9, 26],其数学模型如下
式中,Vi1为其他观测技术获取的垂向速度场投影到地心参考架中的矢量;Vi2为SLR的实测站速度垂向分量投影到地心框架中的矢量;S为两个垂向速度场之间的系统差;Xi为第i站的单位地心矢量;m是测站数。
如果速度场提供的是地心参考架中的站速度,可以通过式(6)把它们换算为站心参考架中沿东、北、垂向的站速度
式中,φi和λi分别是测站i的地心纬度和经度;(Vix,Viy,Viz)为测站i在地心框架中的站速度;(Vie,Vin,Viu)则为测站i在站心参考架中3个方向的站速度。
在系统差模型即式(5)中用到的是各速度场的垂直分量投影到地心框架中的矢量,因此还需将垂直方向的矢量归算至地心坐标参考架,归算公式为
式(4)表示的是两个不同框架下速度场之间的系统差的变化率;而式(5)中的S表示的则是两个垂向速度场之间的系统差,因此,结合式(4)和式(7),即可给出解算两垂向速度场之间系统差的解算方式。
如果式(4)中的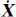 1表示其他技术的垂向速度场;
1表示其他技术的垂向速度场;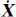 2表示SLR垂向基准,那么两个垂向速度场要归算至地心参考架则可以采用式(7)。结合式(4)和式(7),并忽略旋转参数和平移参数随时间的变率影响,给出误差方程V=AX+L的表达如下
2表示SLR垂向基准,那么两个垂向速度场要归算至地心参考架则可以采用式(7)。结合式(4)和式(7),并忽略旋转参数和平移参数随时间的变率影响,给出误差方程V=AX+L的表达如下
式中,(X,Y,Z)就是两种技术并址台站的直角坐标,而L阵表示的则是并址台站在两框架下的垂向速度在地心参考架下的投影之差,即
为分析其他技术的垂向速度场与SLR垂向基准之间的差异,可以采用一元线性回归分析的方法计算两速度场之间的拟合斜率[9, 24]。假设VV1为一种技术的垂向速度场,VV2为另一种技术的垂向速度场,其拟合函数为
式中,a和b是拟合系数,同时还可通过式(11)计算两垂向速度场之间的相关系数
利用拟合函数和相关系数不仅可以分析其他技术的垂向速度场与SLR垂向基准之间的差异,还可以分析经过系统差模型转换后的速度场与垂向基准之间的一致性,进而分析和探讨以SLR垂向运动作为垂直地壳运动参考基准的合理性。
3.3 结果与分析依据上述建模方法和观测数据,选取SLR与不同框架下GPS、VLBI的并址站(并址站数目见表 2),研究将ITRF2008框架下SLR垂向速度定义为全球垂直地壳运动的参考基准,利用公式(4)、(5)、(7)求解不同框架下GPS、VLBI的垂向速度场相对于SLR垂向参考基准的系统差,即它们之间变换参数的变化率,结果见表 1。
| 数据 | 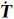 1/(mm/a) 1/(mm/a) | 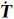 2/(mm/a) 2/(mm/a) | 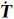 3/(mm/a) 3/(mm/a) | 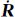 1/(0.001″/a) 1/(0.001″/a) | 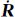 2/(0.001″/a) 2/(0.001″/a) | 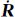 3(0.001″/a) 3(0.001″/a) | 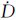 /(10-9/a) /(10-9/a)
|
| ITRF2008_GNSS | 0.047 3 | -0.101 7 | 0.102 7 | -0.002 0 | -0.000 2 | 0.000 4 | 0.071 0 |
| ITRF2008_VLBI | 0.006 5 | -0.175 8 | 0.166 3 | -0.001 3 | 0.000 6 | 0.000 6 | -0.037 6 |
| ITRF2005_GPS | 0.293 3 | -0.166 1 | 0.262 8 | -0.003 0 | -0.003 9 | 0.000 1 | 0.033 9 |
| ITRF2005_VLBI | 1.550 0 | 1.085 6 | 0.870 0 | 0.019 8 | -0.029 9 | 0.003 9 | 0.284 5 |
| VV2-VV1 | 数据状态 | a | b | 相关系数 | 并址站数 |
| ITRF08_SLR-ITRF08_GNSS | 改正前 | 0.574 0 | 0.555 9 | 0.640 4 | 29 |
| 改正后 | 0.567 2 | 0.209 5 | 0.717 2 | ||
| ITRF08_SLR-ITRF08_VLBI | 改正前 | 0.706 2 | -0.314 2 | 0.740 6 | 11 |
| 改正后 | 0.695 3 | -0.138 1 | 0.765 0 | ||
| ITRF08_SLR-ITRF05_GPS | 改正前 | 0.958 6 | 0.114 3 | 0.854 5 | 22 |
| 改正后 | 1.011 7 | 0.340 2 | 0.860 2 | ||
| ITRF08_SLR-ITRF05_VLBI | 改正前 | 0.864 0 | -0.213 5 | 0.897 6 | 9 |
| 改正后 | 1.280 5 | 1.259 8 | 0.935 2 |
为了分析其他技术的垂向速度场与SLR垂向基准之间的差异,采用上述线性回归分析方法求取两者之间的回归系数,利用式(10)和式(11)可以求解不同框架下GPS、VLBI的垂向速度场(表 2中的VV1)相对于SLR垂向参考基准(表 2中的VV2)的拟合斜率和相关系数,结果见表 2,表 2同时还给出了经系统差修正后的速度场与SLR基准之间的拟合斜率(a,b)及相关系数。
由表 1可以看出,将SLR的垂向速度场作为垂向基准,该基准与不同框架下VLBI 和GPS的速度场之间系统差值比较小,平移参数的变化率大都集中在mm/a量级,而旋转参数的变化率也在毫角秒的量级,尺度参数的变化率更小,基本在10-11的量级;从整体来看,求取的系统差的大小及方向各不相同,说明各数据分析中心给出的垂向速度场采用的垂直地壳运动参考基准确实是不统一的。比较表 1中的第2行和第4行的系统差值,可以看出,即使是同一种观测技术在不同的观测历元和时间跨度的速度场,其垂直地壳运动的参考基准也是不同的;同样,比较第3行和第5行的系统差值,也说明同一种技术在不同的参考框架下采用的垂直基准也是不同的。
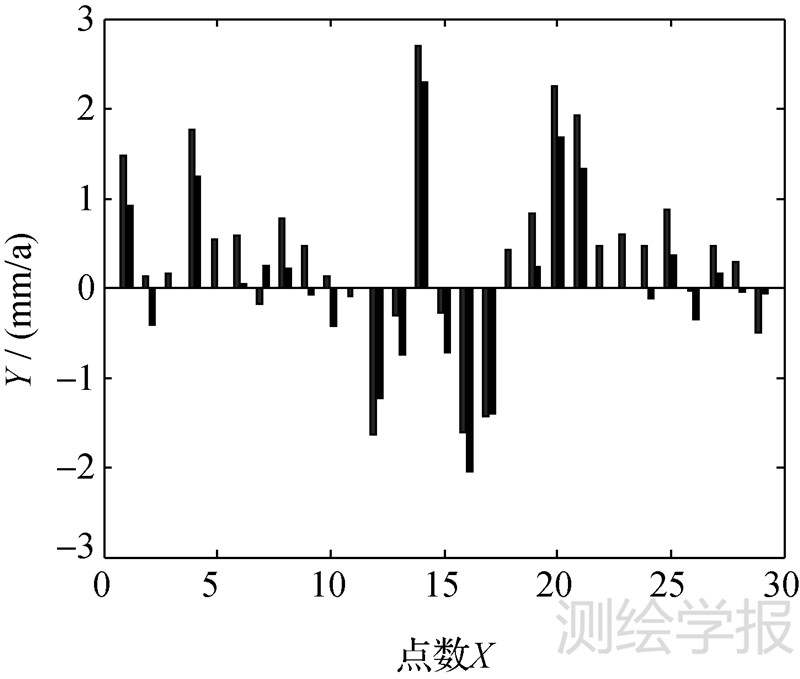
由表 2可以看出,经过系统差改正后的相关系数都有所提高,即各技术的垂直运动速度场经过系统差改正后与SLR垂直基准之间的拟合程度更好。表 3给出了ITRF2008_GNSS的垂直速度场及其经过系统差改正后的垂向速度场分别与建立的SLR垂向基准之间的比较,图 1是其系统差改正前后与SLR垂直基准之间的差值比较,其中左侧为ITRF2008_GNSS的速度场与SLR垂直基准之间的残差,右侧为经过系统差改正后相应的残差表示。限于篇幅,其他速度场的比较情况不再列出。从上述结果可以看出,经过系统差修正后,整体上来看其与SLR相应台站垂向速度的一致性变好,但有些台站经过系统差改正之后其一致性变差,一方面说明其他技术与SLR技术建立的参考框架之间确实存在着差异,另外在解算系统差的过程中也有可能会引入一些舍入误差。
| Site Name | B/(°) | L/(°) | Vu/(mm/a)改正前 | Vu/(mm/a)改正后 | Vu/(mm/a)SLR |
| GRAS | 43.754 7 | 6.920 5 | 0.949 7 | 0.398 4 | -0.523 4 |
| GRAZ | 47.067 1 | 15.493 4 | 0.975 5 | 0.432 8 | 0.841 7 |
| BOR1 | 52.276 9 | 17.073 4 | -0.198 5 | -0.355 5 | -0.355 3 |
| CRAO | 44.413 2 | 33.990 9 | 0.949 4 | 0.434 2 | -0.812 1 |
| CAGL | 39.135 9 | 8.972 7 | 0.629 2 | 0.082 8 | 0.082 8 |
| MATE | 40.649 1 | 16.704 4 | 1.209 1 | 0.674 8 | 0.631 7 |
| HERS | 50.867 3 | 0.336 2 | -0.489 2 | -0.075 4 | -0.321 1 |
| SFER | 36.464 3 | -6.205 6 | 0.893 8 | 0.330 1 | 0.114 5 |
| ZIMM | 46.877 0 | 7.465 2 | 1.840 7 | 1.289 2 | 1.367 5 |
| WAB2 | 46.923 7 | 7.464 2 | 1.497 7 | 0.945 9 | 1.367 5 |
| POTS | 52.379 2 | 13.066 0 | -0.322 9 | -0.230 9 | -0.230 9 |
| WTZR | 49.144 1 | 12.878 9 | -0.479 3 | -0.070 7 | 1.158 5 |
| BJFS | 39.608 6 | 115.892 4 | 2.638 1 | 2.205 2 | 2.948 2 |
| SHAO | 31.099 6 | 121.200 4 | 1.293 6 | 0.880 6 | -1.412 3 |
| KGNI | 35.710 3 | 139.488 1 | 1.865 0 | 1.432 8 | 2.144 5 |
| MTKA | 35.679 5 | 139.561 3 | 0.540 0 | 0.101 1 | 2.144 5 |
| HRAO | -25.890 1 | 27.686 9 | -0.243 7 | -0.206 7 | 1.190 0 |
| SUTH | -32.380 2 | 20.810 4 | 0.528 3 | 0.100 5 | 0.098 8 |
| ALGO | 45.955 8 | -78.071 3 | 4.140 2 | 3.537 4 | 3.304 4 |
| QUIN | 39.974 5 | -120.944 4 | 1.674 1 | 1.103 1 | -0.571 5 |
| MDO1 | 30.680 5 | -104.014 9 | 1.650 3 | 1.065 3 | -0.269 6 |
| MAUI | 20.706 6 | -156.257 0 | -0.692 0 | -1.162 0 | -1.162 7 |
| GODE | 39.021 7 | -76.826 8 | -0.548 1 | -1.144 7 | -1.144 6 |
| MONP | 32.891 9 | -116.422 3 | 1.362 0 | 0.788 5 | 0.901 3 |
| AREQ | -16.465 5 | -71.492 7 | -0.988 9 | -1.500 5 | -1.869 5 |
| TIDB | -35.399 2 | 148.979 9 | 0.874 7 | 0.551 2 | 0.901 6 |
| YAR1 | -29.046 5 | 115.346 9 | 0.363 5 | 0.057 1 | -0.108 0 |
| STR2 | -35.316 1 | 149.010 1 | 1.187 1 | 0.865 1 | 0.901 6 |
| THTI | -17.577 0 | -149.606 4 | -0.459 8 | -0.013 3 | 0.038 2 |
|
| 图 1 系统差改正前(左)后(右)ITRF2008_GNSS的垂直运动速度场与SLR垂直基准之间的差值比较 Fig. 1 Difference between ITRF2008_GNSS vertical-velocity field and SLR vertical datum before (left) and after (right) systematic bias correction |
令采用的地球引力场模型的3个一阶系数为0,SLR技术利用该方法将参考框架的原点定义到地球质量中心,所以SLR是真正相对于地心的。由测地VLBI的基本原理可知,VLBI技术是一种纯几何测量,它对地球质心不敏感,在建立参考框架时,通常是利用与SLR并址的某个站的站坐标及相关的基线矢量确定,即VLBI技术建立的参考框架不是真正相对于地心的。虽然高精度的GPS测量是一种相对测量,但GPS技术在求解时通过使所采用的地球引力场3个一阶系数为零来保证测站坐标是相对于地心的,因此利用GPS技术建立的参考框架是相对于地心的,但不如SLR技术更直接,故其地心位置精度不高[24]。
综上所述,将SLR技术获取的垂直运动定义为全球垂直地壳运动的参考基准,该基准与各速度场之间的系统差值比较小;而SLR是监测地心运动最为精确的空间观测技术之一,能够直接测定地面台站的地心坐标和相对于地心的运动速度,故将SLR技术获取的垂向速度作为研究全球垂直地壳运动的参考基准是可行的,而且该基准具有最为直接的地球物理意义和几何意义。另外,随着SLR空间观测技术的进步,其观测精度和观测数量都在不断的提升,同时ITRF2008框架下站坐标速度场的获取是基于时间序列,故将SLR技术获取的垂向速度场作为全球垂直地壳运动的参考基准是目前比较合理且可行的一种实现方法。
4 结 论地壳的垂直运动关乎着人们的生存环境,因此,对其基准进行研究并在全球范围内进行统一,是具有深远意义的。本文从研究建立全球统一的垂直地壳运动基准的必要性开始,对提出的SLR垂向运动基准的方案进行了分析和讨论,并利用相应的实测数据进行了验证,得出如下结论:
(1) SLR技术通过观测地面站至人造卫星的距离来解算地面站相对于地球质心的位置,即利用该技术能够直接测定地面台站的地心坐标,因此利用SLR技术获取的台站垂向速度即为台站相对于地心的运动速度。即将ITRF2008框架下SLR技术获取的垂向速度场定义为全球垂直地壳运动参考基准的方法是合理可行的,而且该基准包含了较为丰富的地球物理信息,具有可发展、可提高以及直接相对于地球质心等特性。
(2) ITRF2008坐标框架基准对原点的定义采用的就是SLR的数据,将更容易使点位坐标框架与点位的垂直运动框架统一起来。因此推荐将ITRF2008框架下SLR技术获取的垂向运动作为全球垂直地壳运动的参考基准。文中利用ITRF的速度场数据对该基准进行了检验,由于ITRF在实现其框架时已作过框架内部之间的整合[21],所以本文解算的系统差值偏小,鉴于篇幅有限,未能列出其他形式的数据(比如全球各数据分析中心在各自框架下解算的数据)对该基准的验证,而本文系统阐述垂直基准统一的相关方法对于建立全球垂直基准、区域垂直基准都有借鉴意义。
| [1] | GU Guohua. Vertical Crustal Movement Obtained from GPS Observation in Chinas Mainland [J]. Earthquake, 2005, 25(3):1-8.(顾国华. GPS观测得到的中国大陆地壳垂直运动[J]. 地震, 2005, 25(3):1-8.) |
| [2] | SUN Fuping, LI Jianwen. Definition and Realization of the Chinese Terrestrial Reference Frame [J]. Journal of Institute of Surveying and Mapping, 1997, 14(4): 241-245.(孙付平, 李建文. 中国地区高精度地球参考架的定义和实现[J]. 解放军测绘学院学报, 1997, 14(4): 241-245.) |
| [3] | DONG Hongwen, WANG Wenli, YAO Renping. Establishment of Single Point Dynamic Vertical Datum in China [J]. Science of Surveying and Mapping, 2002, 27(1): 28-30.(董鸿闻, 王文利, 姚任平. 我国单点动态垂直基准的建立[J]. 测绘科学, 2002, 27(1): 28-30.) |
| [4] | ZHANG Qin, FAN Yizhong. The Isostatic Theory and the Mathematical Model of Crust Vertical Movement [J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3):233-237.(张勤, 范一中. 地壳垂直运动的均衡理论及其分析模型[J]. 测绘学报, 2001, 30(3):233-237.) |
| [5] | ZHANG Qin, FAN Yizhong, ZHAO Chaoying. Analysis Model of Crustal Vertical Movement Based on the Flux Isostasy[J]. Geomatics and Information Science of Wuhan University, 2004, 29 (3):231-234. (张勤, 范一中, 赵超英. 基于通量均衡基准的地壳垂直形变场分析模型[J]. 武汉大学学报:信息科学版, 2004, 29 (3):231-234.) |
| [6] | ZHANG Qin, ZHAO Chaoying. The Spherical Cap Harmonic Analysis Method for Crust Vertical Deformation Field Fitting [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 39-42.(张勤, 赵超英. 地壳垂直形变场逼近的球冠谐分析法[J]. 测绘学报, 2004, 33(1): 39-42.) |
| [7] | ZHANG Yongzhi. The Discussion on Isostatic Instability Condition of Vertical Crustal Movement [J]. Inland Earthquake, 1992, 6(1): 39-45.(张永志. 垂直地壳运动的均衡失稳条件探讨[J]. 内陆地震, 1992, 6(1): 39-45.) |
| [8] | SUN Fuping, ZHAO Ming, NING Jinsheng, et al. Asymmetrical Global Tectonic Changes Based on the Space Geodetic Measurements[J]. Chinese Science Bulletins, 1999,44(20): 2225-2229.(孙付平, 赵铭, 宁津生,等. 用空间大地测量实测数据检测地球的非对称性全球构造变化[J]. 科学通报, 1999, (20): 2225-2229.) |
| [9] | ZHU Xinhui. Study on Space Geodynamics [D]. Zhengzhou: Information and Engineering University, 2005.(朱新慧. 空间地球动力学若干问题研究[D]. 郑州:信息工程大学,2005.) |
| [10] | JIANG Zhihao, ZHANG Peng, BEI Jinzhong,et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame [J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471-475. (蒋志浩, 张鹏, 秘金钟,等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J]. 测绘学报, 2009, 38(6): 471-475.) |
| [11] | JIANG Zhihao, ZHANG Peng, BEI Jinzhong,et al. Velocity Estimation on the Colored Noise Properties of CORS Network on China Based on the CGCS2000 Frame [J]. Acta Geodaetica et Cartographica Sinica, 2010, 30(4): 355-363. (蒋志浩, 张鹏, 秘金钟,等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 30(4): 355-363.) |
| [12] | WEI Ziqing, LIU Guangming, WU Fumei. China Geodetic Coordinate System 2000: Velocity Field in Mainland China [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410. (魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系:中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410.) |
| [13] | ZHAO Lihua, YANG Yuanxi, WANG Qingliang. Collocation Model Based on Regional Tectonic Features in Crustal Deformation Analysis [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 435-441. (赵丽华, 杨元喜, 王庆良. 考虑区域构造特征的地壳形变分析拟合推估模型[J]. 测绘学报, 2011, 40(4): 435-441.) |
| [14] | JEKELI C,DUMRONGCHAI P. On Monitoring a Vertical Datum with Satellite Altimetry and Water-level Gauge Data on Large Lakes [J]. Journal of Geodesy,2003,77: 447-453. |
| [15] | AMOS M J,FEATHERSTONE W E. Unification of New Zealands Local Vertical Datums: Iterative Gravimetric Quasigeoid Computations[J]. Journal of Geodesy,2009,83:57-68. |
| [16] | ARGUS D F, GORDON R G. No-Net-Rotation Model of Current Plate Velocities Incorporate Motion Model NUVEL-1[J]. Geophysical Research Letters, 1991, 18(11): 2039-2042. |
| [17] | DEMETS C. Effect of Recent Revisions to the Geomagnetic Reversal Time Scale on Estimates of Current Plate Motions [J]. Geophysical Research Letters, 1994, 21: 2191-2194. |
| [18] | YAN Fengxuan, GUO Tangyong, WANG Peiyuan, et al. Prospect of Application of SLR- on GALILEO Plan and Debris Tracking[J]. Journal of Geodesy and Geodynamics, 2006, 26(3): 118-121.(严奉轩, 郭唐永, 王培源,等. SLR应用展望-伽利略计划和非合作目标跟踪[J].大地测量与地球动力学, 2006, 26(3): 118-121.) |
| [19] | SUN Fuping, WU Bin, YI Weiyong. Research Progress in the Motions of the Earths Center of Mass [C]//Proceedings of 7th National General Meeting of China Surveying and Mapping Association Haikou:[s.n.], 2001: 135-143.(孙付平, 吴斌, 易维勇. 地球质心运动的研究进展[C]//中国测绘学会第七次全国会员代表大会论文集.海口:[s.n.],2001:135-143.) |
| [20] | GUO Jinyun, CHANG Xiaotao, HAN Yanben, et al. Periodic Geocenter Motion Measured with SLR in 1993-2006[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 311-317.(郭金运, 常晓涛, 韩延本,等. 由SLR观测的地心周期性运动(1993-2006 年)[J]. 测绘学报, 2009, 38(4): 311-317.) |
| [21] | ALTAMIMI Z, COLLILIEUX X, METIVIER L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame [J]. Journal of Geodesy, 2011, 85:457-473. |
| [22] | SUN Fuping. Research of Current Crustal Motions Based upon Space Geodetic Techniques [D]. Shanghai: Shanghai Observatory, 1994.(孙付平. 基于空间技术的现代地壳运动研究[D]. 上海: 上海天文台,1994.) |
| [23] | HERMANN D. The Actual Plate Kinematic and Crustal Deformation Model APKIM2005 as Basis for a Non-rotating ITRF [C]//Geodetic Reference Frames, International Association of Geodesy Symposia. Berlin:[s.n.], 2009: 95-99. |
| [24] | ZHU Xinhui, SUN Fuping. Detection of Postglacial-rebound by Using VLBI Data [J]. Chinese Journal of Geophysical, 2005,48(2):308-313.(朱新慧, 孙付平. 用甚长基线干涉测量数据检测冰期后地壳回弹[J]. 地球物理学报, 2005, 48(2): 308-313.) |