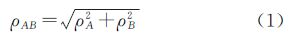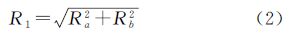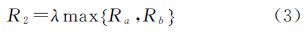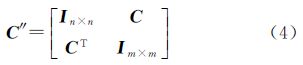2. 浙江中科空间信息技术应用研发中心, 浙江 杭州 314100;
3. 中南大学 地球科学与信息物理学院,湖南 长沙 410083
2. Zhejiang-CAS Application Center for Geoinformatics, Hangzhou 314100, China;
3. Institute of Geoscience and Info-Physics, Central South University, Changsha 410083, China
整合和更新来自不同来源、不同比例尺、不同时间段的表示同一地图目标的地理数据越来越引起人们的关注。空间面状地物和自然要素在很多地图表示中都占有很大的比例,可以用来表示房屋、土地利用、面状水体和植被等,它是地图表达和地图使用者关心的主要内容,本文主要讨论多尺度空间面实体的匹配。空间面实体数据主要有空间特征和属性特征,空间特征主要包括几何特征和拓扑特征,几何特征主要包括重心位置、中心位置、面积大小和边界[1],拓扑特征主要包括面积重叠度、属性成分关联度;属性特征主要是使用实体的属性信息。
空间面匹配,国外学者作过大量的研究。在几何匹配方面,文献[2]提出面质心结合多种匹配检验规则的几何匹配方法,通过面实体栅格化后收缩来确定质心,然后将其矢量化,用点在面内的规则进行粗匹配,再结合多边形的面积A和面密度C进行匹配检验,最终判断匹配情况。文献[3]通过匹配面的边界来计算边界的距离来检测不同时间点的空间面的明显不同,该方法适合于明确的边界的面数据,不适合于大量变化的地形数据。文献[4]提出一种基于邻近关系确定面与面大致的关系,辅助Hausdorff距离来区分面之间的匹配关系,来确定面之间的共轭点,可以用来匹配面数据。语义信息主要取决于空间数据模型和属性数据模型,语义信息可以用来辅助匹配关系。文献[5]提出一种基于知识的非空间属性数据匹配策略,通过计算属性项的相似度值以确定匹配实体。文献[8]提出一种基于语义和结构的相似性的属性数据匹配方法,来匹配正式和非正式的地理数据。
国内学者也作了大量的工作,文献[7]提出基于模糊拓扑关系分类的匹配方法,该方法计算形态距离比较麻烦,只适合于房屋等人工地物。文献[8]在扩展文献[9]的概率论匹配算法的基础上提出一种多准则融合算法,对于面数据,主要采用重心S和面的重叠度A指标,指标的权重是由专家经验来获取的。文献[10]提出基于相似性的面实体匹配方法,该方法适合于相似比例尺的地图数据的匹配。文献[11]提出了基于成分关联区域相似度的面实体模糊匹配算法,但模糊分类比较困难,不适合多比例尺数据。文献[12]也提出一种基于几何特征的多尺度的面实体匹配方法,这也是一种基于相似性的匹配方法,需要确定各个指标的权重。
目前的面匹配的算法还存在一些问题。首先,如何确定每个指标的阈值或者权重。需要确定的阈值主要有:缓冲区半径、Hausdorff距离[13]、形态距离[7]、属性相似性[14]。指标的阈值都与比例尺密切相关。概率匹配、相似性匹配虽然都不需要阈值,但是每个指标的权重在不同的比例尺下是不相同的,如何确定权重也是一个难点。面数据由点组成,利用点的精度信息来匹配空间数据,文献[15]等首先使用点距离信息确定匹配,缓冲区大小根据地图的点位精度而定。文献[16, 17]也利用地图中点的误差来实现点的匹配,但是点位误差很难确定。其次,如何确定面的M∶N关系。目前的大多都匹配算法都是基于文献[9]提出的双向匹配策略,但是其方法只适合于点匹配。文献[4]提出用面数据的邻近关系,利用聚集算法可以确定面与面数据之间的多对多的关系的大致关系,再根据Hausdorff距离确定数据之间的精确关系,该距离没有考虑多尺度情况下的匹配,需要统计数据才能确定范围。最后,很难确定数据匹配不确定性的范围,错误信息的范围对人工交互的过程有重要的影响。文献[18]提出一种基于证据理论来匹配点目标,但是计算每个指标的信任度仍然是一个经验的过程。
根据制图误差理论,中误差作为数据质量和地图综合的指标,而且其大小范围随着比例尺的变化而变化,可以有效地应用于多尺度空间数据的匹配,并可以确定数据不确定性的范围。本文在文献[4]提出的邻近关系匹配的基础上,提出一种基于中误差和邻近关系的多尺度空间面实体匹配算法,不仅可以确定准确的数据范围,同时可以确定不确定性的匹配范围,同时考虑了不同比例尺下制图综合的影响,可以有效应用于多尺度面实体匹配。
2 基于中误差和邻近关系的算法原理 2.1 中误差中误差是衡量观测精度的一种数字标准,亦称“标准差”或“均方根差”。它是观测值与真值偏差的平方和与观测次数n比值的平方根。点位误差表示点位的观测值与真值之差,制图规范中的点位误差用地物点和控制点的位置中误差来衡量。点位误差概率分布曲线呈正态分布或类正态分布[21]。点误差的大小通过中误差来衡量,其概率分布满足正态分布的点位误差表示99%以上的点都分布2倍中误差以内,中误差的大小随着数据源的不同而变化,但是传统的规范制图中规定同比例尺中误差的范围是固定的,该范围随着比例尺的变大而变大,中误差σ必须满足-σmax≤σ≤σmax。文献[19]提出相互误差范围(mutual-error)表示不同来源空间数据之间的误差,假设空间数据点A和B,ρA、ρB分别表示A和B数据点位误差的大小,则相互误差范围ρAB的大小为
ρAB确定了A和B中相应的点的最大距离[17]。但是直接利用相互误差范围存在两个问题:首先,面状地物主要由点组成,组成面状地物的点与点之间不一定存在对应关系;其次,空间数据的点位误差信息很难获得。虽然空间数据的点位误差分布是随机的,但是,其大小必须满足制图规范中对误差的要求。其范围大小在一定的范围内,假设A和B数据的中误差大小的范围为Ra、Rb,由于点位误差概率分布曲线呈正态分布,则可得
大部分的多分辨率地理数据都在R1的范围内,99%的数据都在R2的范围内(由制图规范可以知道城市地形图中取λ=2),不同比例尺数据的中误差大小的范围都可以在制图规范中查到。如果空间数据有明确的点位误差信息,也可以用ρAB作为R1的距离。目前的基于概率、相似性的面匹配算法,虽然可以通过重叠面积的比例来确定要素的关系,但没有考虑多比例尺下和制图综合的过程多数据的影响。在1∶500比例尺,要素主要判断为1∶1关系,但是在1∶10 000情况下,考虑制图综合的因素,可能判断为1∶0的对应关系。如果仅以距离的大小或者重叠的面积判断,会出现明显的错误,其阈值也很难确定。
2.2 匹配关系面状要素的关系主要有1∶0、1∶M(M>1)、1∶1、M∶1(M>1)、M∶N(M>1,N>1)、0∶1关系,图 3所示的面要素S对于匹配的候选要素集T,主要的匹配关系有以下4类:
|
| 图 3 案例数据集 Fig. 3 英文标题 |
(1) 一对零关系。S或者T不包含任何对应的匹配要素,对应的匹配关系为1∶0、0∶1关系。
(2) 一对一关系。S和T的对应关系为1∶1关系。
(3) 一对多关系。S和T的对应关系为1∶M(M>1)、M∶1(M>1)关系。
(4) 多对多关系。S和T的对应关系M∶N(M>1,N>1)关系。
为了确定要素之间的关系,常用Hausdorff距离来度量这种关系。关于要素S和候选T对应的Hausdorff距离,文献[13]也提出一种扩展的Hausdorff距离来计算面之间的关系。Hausdorff距离很难反映数据的多尺度变化。本文使用点位误差密切相关的中误差距离d来表示不同面要素之间的对应关系,d距离表示地物相离的程度。
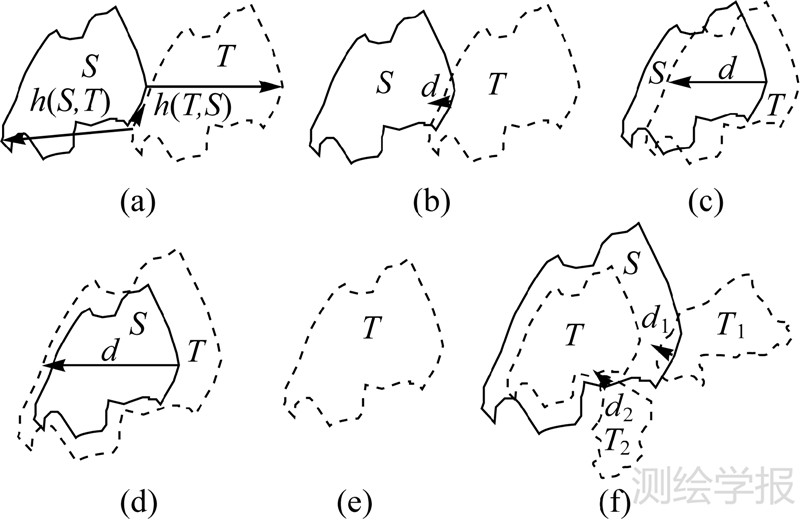
图 1所示的几种典型的面状地物的对应关系,假设匹配的要素相互误差的限差为δ(对应于式(1)或式(2))。要素之间的对应关系可以通过中误差距离来确定,面状要素之间的对应关系都可以通过距离和限差的大小来确定,在图中:
|
| 图 1 面状要素关系 Fig. 1 Multi-scale polygon relations |
(1) 如图 1(a)所示,要素S和T相离,对于S要素的对应关系为1∶0关系,而对于T要素为0∶1关系。图 1(e)所示,要素T没有候选要素,也为0∶1关系。
(2) 如图 1(b)、1(c)所示,要素S和T相交,在图 1(b)中,如果中误差距离d<δ,则对于S要素,其对应关系为1∶0关系,而对于T为0∶1关系;如果中误差距离d>δ,则要素的对应关系为1∶1关系。在图 1(c)所示的关系中,明显可以看出d>δ,对应的关系为1∶1关系。
(3) 如图 1(d)所示,要素S包含于要素T,可以明显可以看出要素的对应关系为1∶1关系。
(4) 如图 1(f)所示,要素S和T、T1、T2叠置,T要素包含于S,T1、T2和要素S相交,其关系主要取决于d1、d2和δ的大小关系。
如上文的分析可以知道,要素之间的对应关系主要取决于要素之间的中误差的距离的大小。通过比较中误差距离和相互误差限差δ的大小,可以确定面与面之间一对零关系、一对一关系、一对多关系。对于多对多关系,可以通过邻近关系来确定。
2.3 邻近关系对于多对多匹配关系也是一个匹配的难点问题,引入邻近关系来完成面与面之间最终的匹配。M∶N匹配实际上是一个聚类问题,表示分别用M面和N面来表示同一个地物目标。文献[20]提出利用邻近关系来合并分散的面片,文献[6]在此工作的基础上用面与面之间的叠置关系来确定面之间关系。前面可以通过计算中误差距离可以初步确定要素的对应关系,可以充分利用上一步匹配过滤之后的匹配成果来完成M∶N匹配。假设“源数据”中A有M要素(Ai,i=1,2,…,M),目标数据集B有对应的N要素(Bj,j=1,2,…,N),构建链接关系矩阵C,如果Ai和Bj有相交关系,C(i,j)的值为1,构建如下的方程
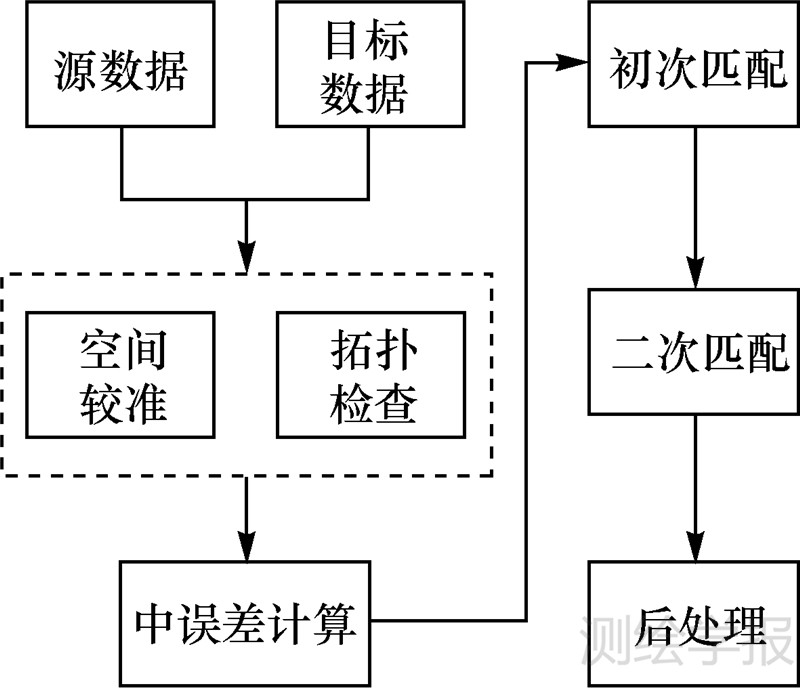
式中,Im×m、In×n表示单位矩阵。通过对C″做D次相乘可以得到数据之间的对应关系,D的次数由于反复自乘之后矩阵中0的个数不发生变化为止。在2.2节中,已经将对应的关系初步确定了,只有M∶N匹配关系了。对于原始要素S对应的候选集合的每个要素,可以反向搜索每个候选要素的对应的叠置的集合,判断要素的方法如2.2节方法一致,并将该要素添加到“源要素”集中,构建M要素集合和N要素集合,最终完成M∶N匹配。 2.4 算法流程整个算法主要是由5个过程组成:① 数据预处理,消除系统误差,检查拓扑关系和建立数据索引;② 确定中误差大小或者范围;③ 初匹配,确定在范围之内的高信任度的几何目标;④ 确定推理弱匹配的要素;⑤ 交互匹配或者检索低信任度的确定的地图要素。整个算法流程如图 2所示。
|
| 图 2 匹配流程图 Fig. 2 The flow diagram of matching process |
为了提高匹配的效率,需要对要素进行预处理,主要包括空间校准、拓扑检查、建立索引。消除系统的误差,首先需要将“源数据”校准到“参考数据集”中[21]。人工采集4个以上的控制点,利用最小二乘原理将“源数据”校准到参考数据集中。
2.4.2 中误差范围依据GB14912-94,在1∶1000比例尺中,一般地区σmax=0.3 m,对于1∶5000比例尺,一般地区σmax=2.5 m;而在1∶10 000比例尺中,一般地区为σmax=5.0 m。数据制图中总的精度根据具体的制图情况来确定,空间数据中误差概率分布曲线呈正态分布,2倍中误差为最大的误差范围。尽管每个地物的点位误差信息都是变化的,但是其点位中误差都是在一定的范围之内。
2.4.3 初始匹配面状要素的关系主要有:① 一对零关系;② 一对一关系;③ 一对多关系;④ 多对多关系。第一步初步确定一对一关系和一对多关系,之后再确定多对多关系。对于单个源要素S,确定其候选要素,首先对S要素做拓扑交运算得到候选要素集合T。主要的匹配过程为:
(1) 如果候选集合的个数为0,则对应为①或②类型,再对要素进一步作拓扑包含运算,如果拓扑包含的要素个数为0,对应为①类型,否则到步骤(2)。
(2) 如果拓扑包含的集合的个数不为0,对S以R1为半径做缓冲区得到要素c。对候选集的每个要素和缓冲区要素c作拓扑包含运算,如果全部的要素都在c的范围内,要素的数目为1,则对应为②类型。否则对应为③关系。
(3) 步骤(2)中如果候选要素不全在c要素内,可能的类型为③型和④型,需要对候选要素作拓扑交运算。如果候选的要素有和S相交的要素,则需要反向计算该要素是否在d的范围之内或该要素超过一个对应的要素,如果超过这个范围则这种类型为④类型,否则为③类型。
(4) 通过步骤(3)计算之后,最后只剩下④类型。则需要进一步利用邻近关系来确定数据的匹配关系。
(5) 利用邻近关系来确定多对多匹配的关系。
(6) 对要匹配的要素,反向重新计算一次,找到0∶1的匹配关系和M∶1关系,计算过程和前面类似。
2.4.4 二次匹配由式(1)—式(3)所知,R1的初始搜索范围可以通过式(1)或者式(2)可以获得,表示了大部分的数据的误差范围,如果有精确的点位误差,可以用式(1)计算得到,否则通过式(2)获得,R2表示理论上的最大误差的范围。由于数据要素的匹配的要素可能也在R2范围之内,对于没有检索到的要素,扩大检索的范围R1到R2,重复2.4.2 节的过程,进一步提高要素的检索范围,由于前面的匹配有着严格的数学依据,再进一步调整匹配的对应关系。会改变对应的匹配的关系,该部分数据为低信任度的部分数据。
2.4.5 后处理最后,将所有检索到的目标数据集合,匹配方法不可能考虑到所有的情况,但是将有可能出现错误的要素提交给用户,由用户来人工判断和实地检查,从而完成整个匹配的过程。由于第二次匹配的过程中的匹配关系与第一次匹配是有差异,并且多对多匹配的过程最容易发生错误,将第二次更新的关系,提交给最终用户来人工交互检查。
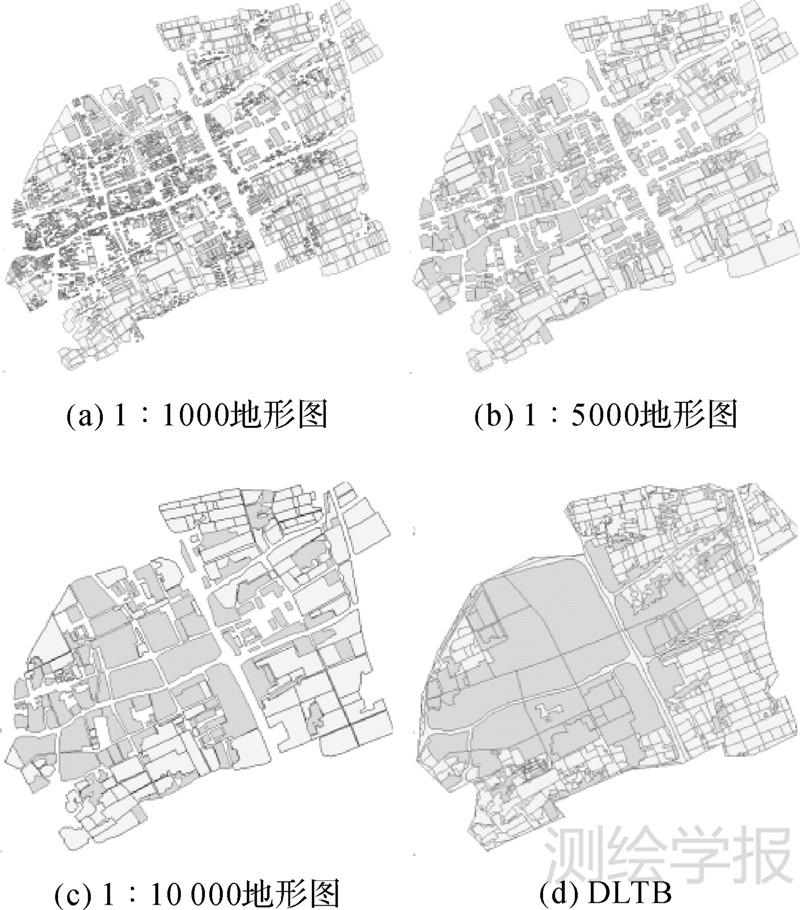
3 试验分析 3.1 试验数据为了验证本文提出方法,利用浙江海盐地区的2012年航空影像人工采集的1∶1000、1∶5000、1∶10 000地形图。该数据可用于城市规划、房产属性、市政建设等方面,各种要素齐全,但是属性信息比较少,分别用A、B、C来表示。还有同一个地区2008年采集的1∶10 000比例尺的第二次土地利用调查数据(DLTB),主要包含是道路、河流和房屋、土地范围等,房屋信息只含村镇的范围信息,但是土地利用的权属信息十分完备。整个研究区范围大小一共是6.6 km2的包含多要素的城市地区。研究区域如图 3所示,表示同一个区的要素,面要素类型主要有居民地和土地。
试验主要的目的是验证算法对多尺度地理数据的匹配适用性,以及相同尺度的下的不同来源和数据模型的数据匹配适用情况。用1∶1000比例尺的地形图数据匹配1∶5000、1∶10 000的地形图数据,来验证同一数据模型下的多尺度面实体匹配适用性;用1∶10 000地形图数据匹配1∶10 000的土地利用调查数据,来验证不同来源和数据模型的面实体匹配适用性。这里数据都不知道每个数据点位误差准确的大小,根据制图误差理论,1∶1000、1∶5000、1∶10 000的中误差范围大小为0.3 m、2.5 m、5.0 m。
| 源比例尺 | 目标比例尺 | R1/m | R2/m |
| 1∶1000 | 1∶5000 | 2.52 | 5.0 |
| 1∶1000 | 1∶10 000 | 5.01 | 10.0 |
| 1∶10 000 | DLTB | 7.07 | 10.0 |
评价算法的精度是整个匹配过程中非常重要的一步,主要用检索率和准确率评价结果,检索率表示自动检索的目标对和人工交互检索的目标对的数目的百分比,准确率表示检索的目标对的正确率[9]。表 2表示不同比例尺数据的匹配结果。可以进一步扩大误差R2的范围,将变化的匹配关系提交给用户,由人工进行交互检查,提高匹配的精度。
| 源数据 | 目标数据 | 1∶0 | 1∶M | M∶N | 0∶1 | 准确率/(%) | 检索率/(%) |
| 1∶1000 | 1∶5000 | 245/245 | 447/448 | 412/417 | 7/7 | 99.5 | 100 |
| 1∶1000 | 1∶10 000 | 179/182 | 62/62 | 191/194 | 5/5 | 98.6 | 100 |
| 1∶10 000 | DLTB | 62/62 | 27/27 | 80/81 | 29/31 | 98.5 | 100 |
如表 2所示,在1∶M匹配关系中,1∶1000和1∶5000比例尺下空间数据匹配的结果为447/448,其表示算法自动检测出空间数据的匹配对为448对,其中447对为正确,其余匹配结果表示含义类似。本文的算法主要是通过重叠度来检索数据,如果数据存在重叠都能全部检索到,检索率分别率都达到100%。对于多尺度空间面数据匹配也有很好的匹配准确率,准确率分别都达到99.5%、98.6%、98.5%。对应的4种匹配关系中,多对多匹配的匹配精度相对低一些。
3.2.2 算法比较多比例尺数据匹配,文献[2]提出栅格质心和重叠面积,采用概率的方法来确定要素的对应关系;文献[8]提出的概率算法,和文献[2]很相似,但是都存在指标的权重难确定的问题。文献[4]主要采用要素的扩展Hausdorff距离来确定要素之间的对应关系,该方法是一种统计的计算方法。此外文献[10]提出的相似性匹配算法,该方法也存在指标的权重问题,该方法的边界指标不适合于比例尺变化大的数据。本文主要是与文献[4, 8, 10]进行比较。本文试验采用是在1∶10 000比例尺下地形图和土地利用图(DLTB)进行比较。文献[8]中的概率算法,取重心指标和面积重叠度指标,假设每个指标的权重都为1。文献[10]中的相似性匹配算法,取中心指标、边界指标、面积大小指标,假设每个指标的权重都为1。文献[4]的邻近关系匹配主要采用扩展Hausdorff距离来确定。统计结果见表 3、表 4。
| 方法 | 1∶0 | 1∶M | M∶N | 0∶1 | 检索率/(%) |
| 概率 | 38/62 | 141/27 | 29/81 | 33/31 | — |
| 相似性 | 20/62 | 26/27 | 83/81 | 22/31 | 72.5 |
| Hausdorff | 46/62 | 27/27 | 79/81 | 24/31 | 87.6 |
| 中误差 | 62/62 | 27/27 | 81/81 | 31/31 | 100 |
| 方法 | 1∶0 | 1∶M | M∶N | 0∶1 | 准确率/(%) |
| 概率 | 43/43 | 86/141 | 16/29 | 29/29 | 71.9 |
| 相似性 | 20/20 | 18/26 | 15/83 | 22/22 | 49.7 |
| Hausdorff | 42/46 | 17/27 | 60/79 | 22/24 | 81.1 |
| 中误差 | 62/62 | 27/27 | 80/81 | 29/31 | 98.5 |
从表 3可以看出,概率匹配算法不需要每项指标的阈值,对于空间数据有很小的叠置都识别为1∶M关系,其主要对面的匹配概率大小的比较来确定空间数据的匹配关系。对于多对多匹配关系,比较难确定,将很多的多对多匹配关系,识别为1∶M关系。相似性、Hausdorff距离和中误差的方法的检索率分别达到72.5%、87.6%、100%。从表 4可以看出,对于不同的匹配方法,对于1∶0和0∶1匹配,各种不同的匹配方法精度都差不多,算法的效率主要取决于1∶M和M∶N匹配的精度,4个算法精度分别达到71.9%、49.7%、81.1%、98.5%。和相似性匹配算法、Hausdorff距离和概率匹配算法比较,本文提出的基于中误差和邻近关系的面匹配方法有着明显的提高。
将检索距离扩展到在R2范围下,多检索出7对1∶0匹配的情形,同时少检索出5对多对多匹配的情形,将之匹配为1∶M的情形,变化的关系为低信任度的关系。根据制图误差理论,如果对应点的误差超过R2范围,则表示不是同一个目标。
4 结论和讨论本文根据制图误差理论,利用空间数据的中误差范围信息和数据邻近关系来匹配多尺度空间面实体数据。利用中误差信息可以有效地提高初始搜索到准确率,首先确定1∶0以及1∶M关系,通过建立邻近关系矩阵来确定数据的多对多关系,并通过扩大范围确定相对低一些的信任度的匹配关系,接着将这些关系进行人工交互处理,最终完成整个匹配的过程。和已有的方法比较,本算法具有良好的准确度和效率,试验结果表明该方法具有有效性和实用性。
本算法有以下几个方面的特点:首先,不需要专家经验或统计学习的方法确定每个指标的阈值。中误差范围只是由匹配的目标尺度决定,不受地图综合和制图方法的影响。其次,依据制图误差理论,可以适用于各种来源不同比例尺的地理数据。再次,算法从高信任度的匹配数据来推理相对信任度的数据,同时将低信任度交给用户交互,进一步提高了匹配的效率,更符合数据生产的过程。
最后,本文的方法适用于严格的制图规范下的多尺度地理数据的匹配,不一定适用于没有按照制图规范制作的志愿者地理数据。志愿者地理信息作为空间数据的一个新的重要的来源,如何有效地整合志愿地理数据和传统的数据,是下一步研究的方向。
| [1] | WENTZ E A. Shape Analysis in GIS[C]//Proceedings of Auto-Carto 13. Seattle: ACSM/ASPRS, 1997: 204-213. |
| [2] | YUAN S X, TAO C. Development of Conflation Components[C]//Proceedings of Geoinformatics 99 Conference. Ann Arbor:[s.n.], 1999: 1-12. |
| [3] | MASUYAMA A. Methods for Detecting Apparent Differences between Spatial Tessellations at Different Time Points[J]. International Journal of Geographical Information Science, 2006, 20(6): 633-648. |
| [4] | HUH Y, YU K, HEO J. Detecting Conjugate-point Pairs for Map Alignment between Two Polygon Datasets[J]. Computers, Environment and Urban Systems, 2011, 35(3): 250-262. |
| [5] | COBB M A, CHUNG M J, FOLEY III H, et al. A Rule-based Approach for the Conflation of Attributed Vector Data[J]. GeoInformatica, 1998, 2(1): 7-35. |
| [6] | AL-BAKRI M, FAIRBAIRN D. Assessing Similarity Matching for Possible Integration of Feature Classifications of Geospatial Data from Official and Informal Sources[J]. International Journal of Geographical Information Science, 2012, 26(8): 1437-1456. |
| [7] | ZHANG Qiaoping, LI Deren, GONG Jianya. Areal Feature Matching among Urban Geographic Databases[J]. Journal of Remote Sensing, 2004, 8(2): 107-112. (张桥平, 李德仁, 龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报, 2004, 8(2): 107-112.) |
| [8] | TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J].Acta Geodaetica et Cartographica Sinaca, 2007, 36(2): 210-217. (童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210-217.) |
| [9] | BEERI C, KANZA Y, SAFRA E, et al. Object Fusion in Geographic Information Systems[C]//Proceedings of the 30th International Conference on Very Large Data Bases: 30. Toronto: VLDB Endowment, 2004: 816-827. |
| [10] | HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinaca, 2008, 37(4): 501-506. (郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4): 501-506.) |
| [11] | YE Yaqin , WAN Bo, CHEN Bo. The Fuzzy Match Algorithm between Area Object Considering Associated Area Similarities[J]. Earth Science: Journal of China University of Geosciences),2010,35(4) :385-390. (叶亚琴, 万波, 陈波. 基于成分关联区域相似度的面实体模糊匹配算法[J]. 地球科学: 中国地质大学学报, 2010, 35(4): 385-390.) |
| [12] | SHAO Shiwei. Researehes and Applications on Polygon Entity Matching for Multi-scale Vector Data Based on Geometric Features[D]. Wuhan: Wuhan University, 2011. (邵世维. 基于几何特征的多尺度矢量面状实体匹配方法研究与应用[D]. 武汉: 武汉大学, 2011.) |
| [13] | DENG M, LI Z L, CHEN X Y. Extended Hausdorff Distance for Spatial Objects in GIS[J]. International Journal of Geographical Information Science, 2007, 21(4): 459-475. |
| [14] | XIONG D, SPERLING J. Semiautomated Matching for Network Database Integration[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 35-46. |
| [15] | GABAY Y, DOYTSHER Y. Automatic Adjustment of Line Maps [C]//Proceedings of the GIS/LIS. Phoenix:[s.n.], 1994:333-341. |
| [16] | SAFRA E, KANZA Y, SAGIV Y, et al. Location-based Algorithms for Finding Sets of Corresponding Objects over Several Geo-spatial Data Sets[J]. International Journal of Geographical Information Science, 2010, 24(1): 69-106. |
| [17] | SAFRA E, KANZA Y, SAGIV Y, et al. Ad hoc Matching of Vectorial Road Networks[J]. International Journal of Geographical Information Science, 2013, 27(1): 114-153. |
| [18] | OLTEANU A-M. A Multi-criteria Fusion Approach for Geographical Data Matching[M]//Quality Aspects in Spatial Data Mining. Boca Raton: CRC Press, 2008: 47-55. |
| [19] | ZANDBERGEN P A. Positional Accuracy of Spatial Data: Non-normal Distributions and a Critique of the National Standard for Spatial Data Accuracy[J]. Transactions in GIS, 2008, 12(1): 103-30. |
| [20] | GOMBOSˇI M, ZˇALIK B, KRIVOGRAD S. Comparing Two Sets of Polygons[J]. International Journal of Geographical Information Science, 2003, 17(5): 431-443. |
| [21] | CHEN C C, KNOBLOCK C A, SHAHABI C, et al. Automatically and Accurately Conflating Orthoimagery and Street Maps[C]//Proceedings of the 12th Annual ACM International Workshop on Geographic Information Systems. Washington: ACM, 2004: 47-56. |